جامع ترین آموزش در حوزه جدول فراوانی ، انواع نمودارهای آماری و نحوه رسم آنها
نمودارهای آماری و جدول فراوانی روش هایی برای دریافت اطلاعات آنی از داده های آماری موجود است. این مقاله یک آموزش کامل و رایگان در مورد نمودارهای آماری و جداول فراوانی را ارائه می دهد. در جدول فراوانی علاوه بر داده ها، فراوانی مطلق، فراوانی نسبی، درصد فراوانی و فراوانی تجمعی وجود دارد. هر کدام از این موارد در این مقاله تعریف می شود. همچنین در این مقاله نمودار میله ای، نمودار هیستوگرام، نمودار خط شکسته، نمودار دایره ای، نمودار حبابی و نمودار راداری معرفی و موارد کارکرد آنها توضیح داده شده است.
برای توصیف و نمایش داده ها چه کارهایی می توانیم انجام دهیم؟
بعد از گرد آوری داده ها، به تنظیم، رده بندی و خلاصه کردن آنها می پردازیم.برای اینکار می توان از روش های زیر استفاده نمود:
- * تنظیم و طبقه بندی داده ها در یک جدول به نام جدول فراوانی
- * رسم کردن نمودارهای مختلف براساس مقادیر جدول فراوانی
چرا به جدول فراوانی نیاز داریم؟
گاهی وقتها به جای داده های واقعی از مقدار تقریبی داده ها استفاده می کنیم در برنامه ریزی های کلان به عددهای واقعی و دقیق نیاز نداریم.
اگر داده های جمع آوری شده زیاد و پراکنده باشند بررسی آنها طولانی می شود. برای اینکه بتوانیم آسان تر و بهتر نتیجه بگیریم داده ها را متناسب با موضوع آماری، دسته بندی و سازماندهی می کنیم.
جدول فراوانی از چه بخش هایی تشکیل شده؟ چطور دسته بندی انجام دهیم؟
برای اینکه داده ها را دسته بندی کنیم نیاز به دانستن یک شاخص پراکندگی به نام دامنه تغییرات داریم. با توجه به آنچه که سوال از ما خواسته دامنه تغییرات را بر طول هر دسته تقسیم کنیم تعداد دسته ها بدست می آید. یا اگر سوال تعداد دسته هایی که لازم دارد را داد باید دامنه تغییرات را بر تعداد دسته ها تقسیم کنیم تا طول دسته بدست آید. اگر دامنه تغییرات را با
و تعداد دسته را با
و طول دسته را با
نشان دهیم داریم:
مرکز دسته: میانگین ( یک شاخص مرکزی) بین بزرگترین داده دسته و کوچکترین داده دسته. که آن را با نشان می دهیم. مرکز
امین دسته را با
نشان می دهیم.
طول دسته: اختلاف بین بزرگترین داده دسته و کوچکترین داده دسته.
فراوانی یا فراوانی مطلق یک داده: تعداد دفعاتی که هر داده مشاهده می شود را فراوانی آن داده می گویند. فراوانی دسته ام را با
نشان می دهیم.
فراوانی نسبی یک داده: ّبا تقسیم فراوانی هر داده به تعداد کل داده ها، فراوانی نسبی آن داده به دست می آید. فراوانی نسبی دسته ام را با
نشان می دهیم.
درصد فراوانی یک داده: اگر فراوانی نسبی داده ها در 100 ضرب شود، آنگاه درصد فراوانی داده ها به دست می آید.
فراوانی تجمعی یک داده: اگر فراوانی هر داده یا دسته را با فراوانی همه ی دسته های قبلی جمع شوند مقدار فراوانی تجمعی آن دسته بدست می آید. فراوانی تجمعی دسته ام را با
نشان می دهیم.
فراوانی نسبی تجمعی یک داده: با تقسیم فراوانی تجمعی هر داده یا دسته از داده ها به کل داده ها، فراوانی نسبی تجمعی داده بدست می آید. فراوانی تجمعی دسته ام را با
نشان می دهیم.
درصد فراوانی تجمعی یک داده: اگر فراوانی تجمعی نسبی داده ها را در 100 ضرب شود، آنگاه درصد فراوانی تجمعی داده ها بدست می آید.
مثال: داده های فرضی 5 و 5 و 7 و 8 و 9 و 10 و 10 و 10 و 12 و 13 و 14 و 14 و 14 و 15 و 15 و 17 و 18 و 19 و 20 و 20 را در نظر بگیرید این داده ها را در 5 دسته قرار دهید.
جواب: برای اینکه داده ها را در 5 دسته تقسیم کنیم ابتدا دامنه تغییرات این داده ها را بدست می آوریم. یعنی بزرگترین داده که 20 هست را منهای کوچکترین داده یعنی 5 می کنیم. که دامنه تغییرات برابر با 15 می شود. حالا باید این مقدار را بر تعداد دسته ها یعنی 5 تقسیم کنیم که طول دسته بدست آید بنابراین طول دسته برابر 3 است.
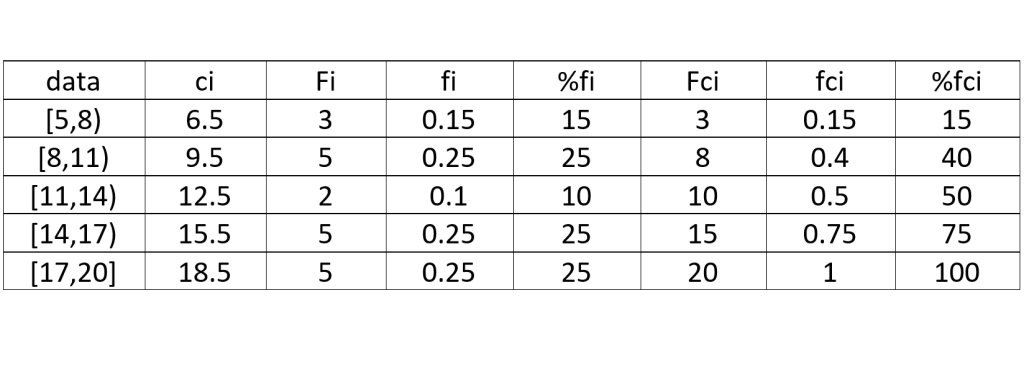
در مرحله بعدی از کوچکترین داده شروع می کنیم و به اندازه طول دسته که برابر با 3 است به آن اضافه می کنیم. به ترتیب به اعداد 5 و 8 و 11 و 14و 17 و 20 می رسیم. حالا طبق جدول زیر دسته بندی را انجام می دهیم و تعداد اعضای هر دسته را می نویسیم.
برای محاسبه مرکز هر دسته باید میانگین اول و آخر هر بازه را بدست آوریم. مثلا برای محاسبه مرکز دسته اول داریم: به همین ترتیب مرکز سایر دسته ها را بدست می آوریم.
برای محاسبه فراوانی هر دسته باید توجه کنیم برای محاسبه تعداد داده های دسته ی باید خود 5 و اعداد بین 5 و 8 را شمرد اما همانطور که در بخش اعداد حقیقی در مورد بازه اعداد خواندیم در این حالت نباید خود عدد 8 را در نظر بگیریم. اما در دسته آخر استثنا داده آخر را در نظر می گیریم توجه کنید که در دسته آخر هر دو طرف بازه
بسته است.
همانطور که کمی پیش تر گفتیم برای محاسبه فراوانی نسبی داده باید فراوانی مطلق هر دسته را بر تعداد کل داده ها که در اینجا 20 تاست تقسیم کنیم (جدا باید تعداد داده ها را بشمارید اگر داده ای سه بار تکرار شده حتما آن را سه بار بشمارید) بنابراین فراوانی نسبی دسته اول برابر است با که برابر است با
است به همین ترتیب برای سایر دسته ها محاسبات را انجام می دهیم.
برای محاسبه فراوانی تجمعی برای دسته اول مقدار فراوانی تجمعی برابر با فراوانی مطلق آن است. اما از دسته دوم به بعد فراوانی دسته مورد نظر را با فراوانی همه ی دسته های قبلی جمع می کنیم. بنابراین فراوانی تجمعی دسته دوم برابر می شود و به همین ترتیب فراوانی تجمعی همه ی دست ها بدست می آید.
انواع نمودارهای آماری
علم آمار علم جمع آوری اطلاعات، سازماندهی و بررسی آنهاست. اطلاعات جمع آوری شده را داده های آماری می گویند. برای مقایسه و بررسی داده های آماری از انواع نمودارها استفاده می کنند. هر نمودار با توجه به به موضوعی که داده های آن جمع آوری شده است و نوع اطلاعات بدست آمده کارایی دارد. برای نمایش داده های یک متغیره از نمودار دایره ای – میله ای- نقطه ای- جعبه ای استفاده می شود و برای نمایش داده های چند متغیره از نمودار حبابی – راداری (عنکبوتی)
نمودار میله ای (ستونی) و نمودار مستطیلی (هیستوگرام)
برای رسم نمودار میله ای چه برای داده ها به صورت آزاد و چه برای داده ها به صورت دسته بندی شده فراوانی هر داده یا دسته را روی محور عرض مشخص می کنیم و از محور طول تا آن مقدار از فراوانی مربوط به آن یک میله رسم می کنیم. در حالتی که داده ها پیوسته باشند نمودار میله ای به صورت مستطیلی رسم می شود.
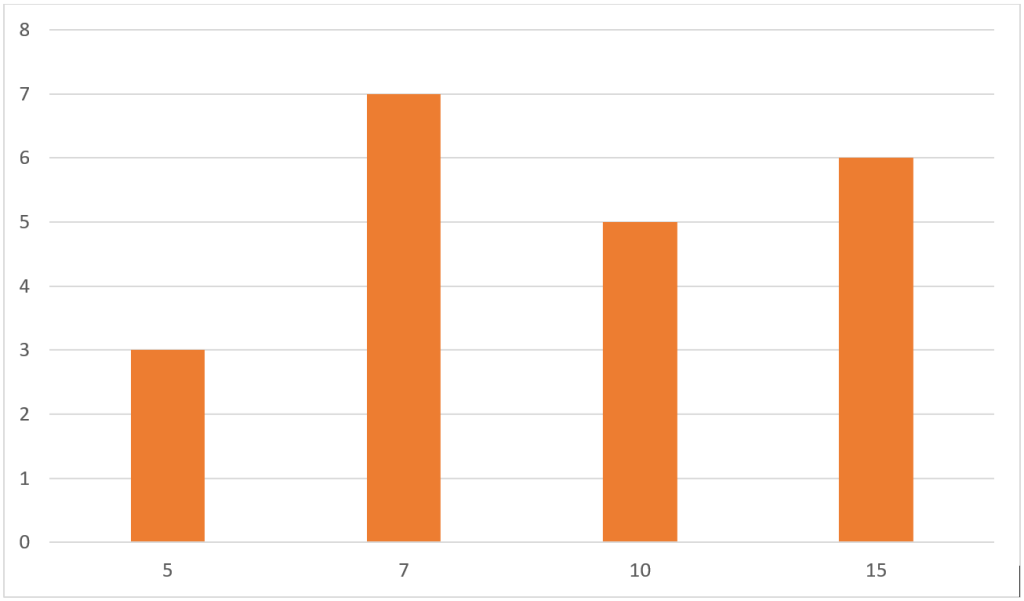
مثلا اگر داده هایی به صورت 5 و 5 و 5 و 7 و 7 و 7 و 7 و 7 و 7 و 7 و 10 و 10 و 10 و 10 و 10 و 15 و 15 و 15 و 15 و 15 و 15 داشته باشیم نمودار میله ای این داده ها به صورت زیر رسم می شود.
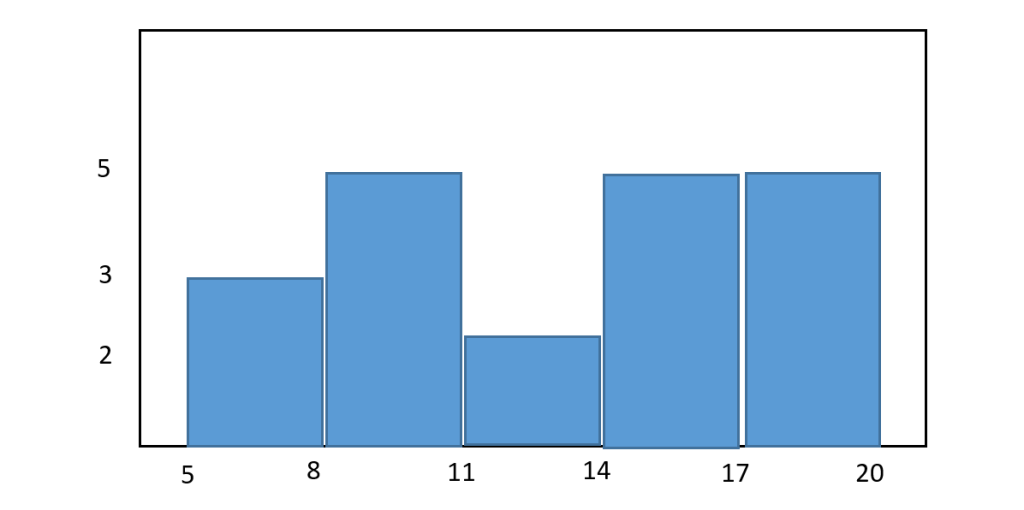
اما برای مثالی که برای آن جدول فراوانی رسم کردیم می توانیم نمودار مستطیلی رسم کنیم به طوری که روی محور افقی بازه ها را مشخص کنیم و فراوانی داده ها را روی محور عمودی مشخص کنیم.
در ادامه چند نکته درباره ی نمودار میله ای و مستطیلی می آموزیم:
- نمودار میله ای برای مقایسه تعداد، پیدا کردن بیشترین و کمترین داده به کار می رود.
- در صورت مقایسه دو دسته داده بهتر است از نمودار میله ای با درصد استفاده کنیم.
- در صورت بررسی یک دسته داده بهتر است از نمودار میله ای با فراوانی استفاده می شود.
- اگر اسم طبقات در متغیر کیفی طولانی باشد نمودار میله ای را افقی رسم می کنیم.
- نمودار میله ای بیشتر برای متغیرهای کمی با مقیاس فاصله ای و متغیرهای کیفی با مقیاس اسمی و ترتیبی (انواع متغیر ها را در مقاله اصطلاحات آماری درباره داده های آماری بخوانید) مناسب تر است.
- برای متغیرهای نسبتی نمودار مستطیلی یا هیستوگرام مناسب تر است.
نمودار خط شکسته
برای رسم نمودار خط شکسته مرکز دسته ها را در نمودار مستطیلی به هم وصل می کنیم. و یک دسته قبل از اولین دسته و یک دسته بعد از آخرین دسته به صورت فرضی با فراوانی صفر در نظر می گیریم.
نکته مهم: نمودار خط شکسته برای نمایش تغییرها کاربرد دارد. بنابراین در موضوعاتی که تغییرات اهمیت دارد از این نمودار استفاده می شود. برای نمونه تغییرها در بازارهای مالی قیمت طلا نفت و سهام را با این نمودار نشان می دهند.
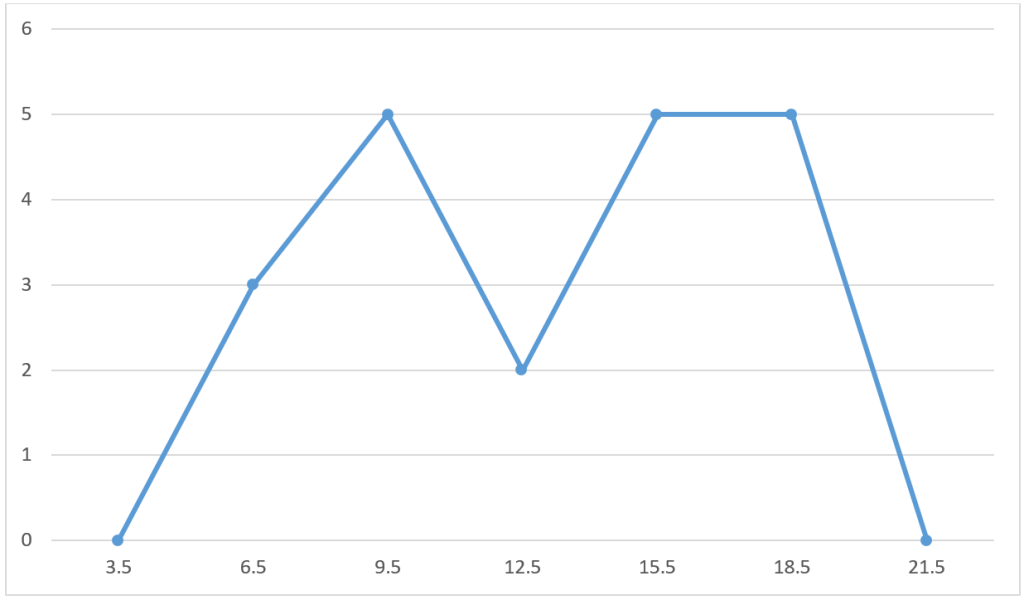
برای مثالی که برای آن جدول فراوانی رسم کردیم نمودار خط شکسته با توجه به مرکز هر دسته و مقدار فراوانی آن به صورت زیر بدست می آید:
نمودار جعبه ای
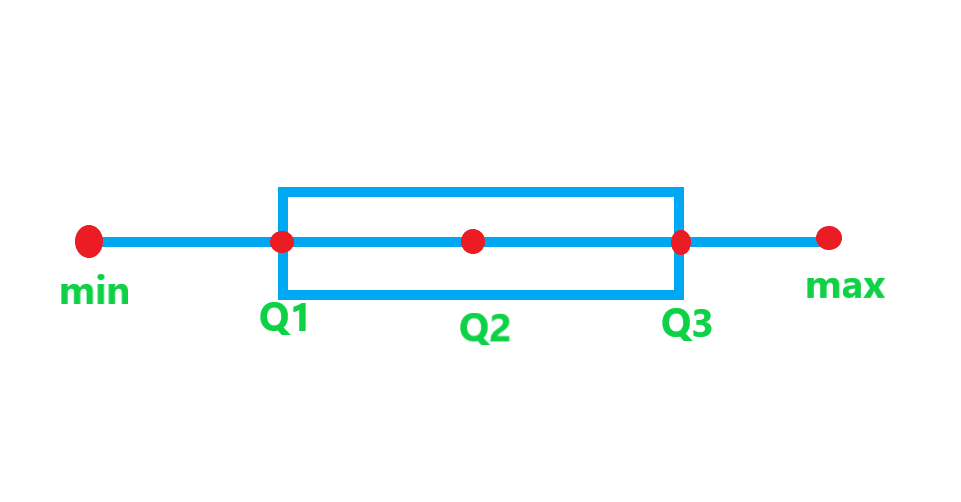
نمودار جعبه ای روشی سودمند برای نمایش دامنه ها و چارک های داده هاست. یک جعبه، مکان قرارگیری چارک ها و دامنه ی میان چارکی را نشان می دهد و سبیل ها کمترین و بیشترین مقادیر داده ها را نشان می دهند. در یک نمودار جعبه ای می توان بیش از یک مجموعه داده را نشان داد پس این نمودار برای مقایسه مناسب است.
با استفاده از نمودار جعبه ای می توان معیارهای پراکندگی داده ها را به صورت تصویری نشان داد.
نمودار بالا یک نمودار جعبه ای را نشان می دهد. در این نمودار چارک اول، میانه، چارک سوم، بیشترین و کمترین داده ها به طور همزمان نشان داده می شوند.
برای رسم نمودار جعبه ای مانند آنچه در مقاله شاخص مرکزی خواندیم باید میانه و چارک اول و سوم داده ها را بدست آوریم.
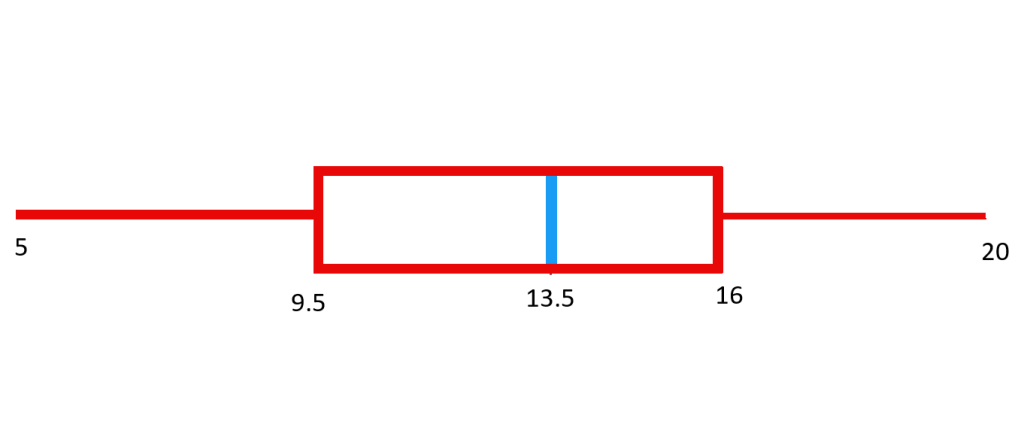
مثلا در مثالی که در ابتدای مقاله حل شد باید میانه 20 داده ی داده های فرضی 5 و 5 و 7 و 8 و 9 و 10 و 10 و 10 و 12 و 13 و 14 و 14 و 14 و 15 و 15 و 17 و 18 و 19 و 20 و 20 را بدست آوریم. دهمین داده 13 و یازدهمین داده 14 می باشد چون تعداد داده ها زوج است میانگین دو داده وسط یعنی دهمین و یازدهمین داده را بدست می آوریم که برابر با 13.5 می شود. چارک سوم برابر میانگین 15 و 17 است که برابر 16 می شود. چارک اول برابر میانگین 9 و 10 می شود که برابر 9.5 می شود. بنابراین نمودار جعبه ای به صورت زیر بدست می آید:
نمودار دایره ای
بعضی از داده ها و اطلاعات جمع آوری شده نشان می دهد که یک مقدار مشخص به چه نسبتی به بخش های کوچک تر تقسیم شده است. در این موارد می توان تقسیم شدن را روی یک شکل مثل دایره نشان داد و سهم هر بخش را روی دایره مشخص کرد. در نمودار دایره ای به طور معمول نسبت و سهم هر بخش را بصورت درصد محاسبه کرده و سپس روی نمودار نمایش می دهند.
نمودار دایره ای بیشتر برای متغیر کیفی (انواع متغیر ها را در مقاله اصطلاحات آماری درباره داده های آماری بخوانید) که دارای حالات کمتری است استفاده می شود هر قطعه از نمودار دایره ای با توجه به زاویه مرکزی که از رابطه بدست می آید مشخص می شود. که در آن
زاویه،
تعداد داده ها و
فراوانی داده ی
ام می باشند.
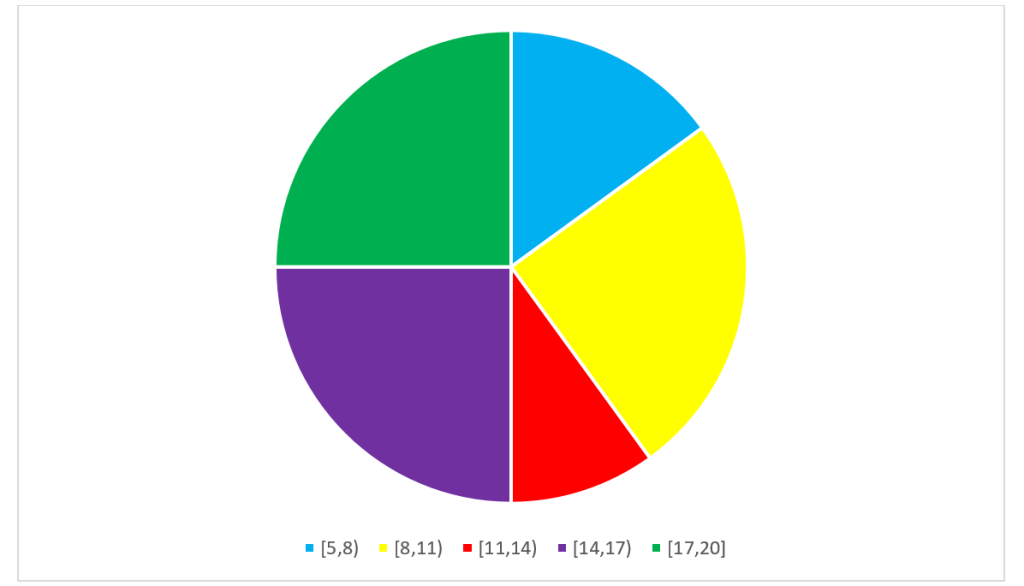
مثلا برای رسم نمودار دایره ای برای داده های فرضی 5و5و7و8 و9و10و10و10و12و13و14و14و14و 15و15و 17 و 18 و 19 و 20 و 20 با 5 دسته می توانیم طبق جدول فراوانی ای که رسم کردیم نمودار دایره ای نظیر آن را به صورت زیر رسم کنیم.
نمودار حبابی
نمودار حبابی نوع خاصی از پراکنش نگاشت است که هم زمان سه متغیر عددی (موقعیت در محور افقی موقعیت در محور عمودی مساحت دایره) در آن بکار می رود و در آن به جای نقطه از دایره های توپر استفاده می شود. شعاع هر دایره برابر جذر متغیر سوم است.
نمودار حبابی در این نمودار به جای نقطه از دایره هایی با مساحت متناظر با ویژگی داده ها رسم می شود. هر نقطه یا دایره در نمودار حبابی یک سه تایی مرتب است که بصورت مشخص می شود که در آن
موقعیت روی محور افقی،
موقعیت روی محور عمودی ،
اندازه نقطه (مساحت دایره) می باشند.
- نمودار حبابی برای نمایش همزمان سه متغیر عددی یا بیشتر به کار می روند.
- نمودار حبابی برای نمایش چند متغیر عددی در یک نمودار به کار می رود؟ محدودیتی ندارد.
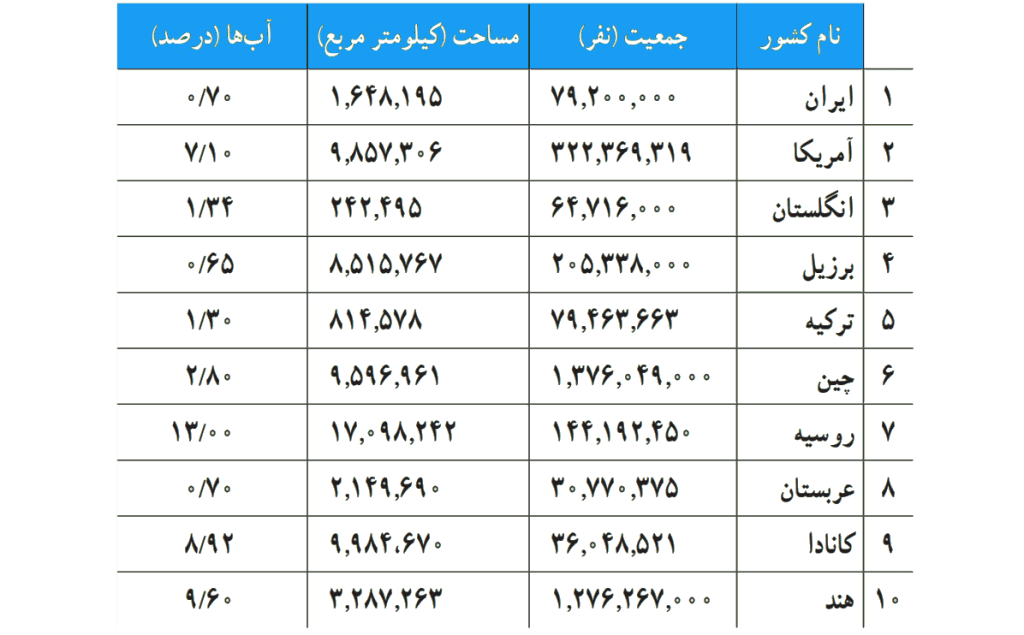
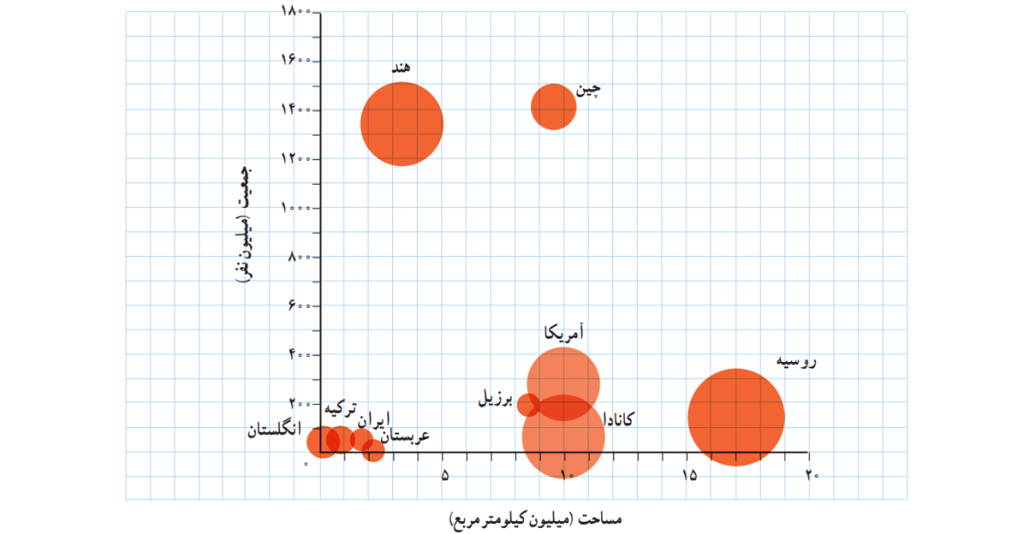
یک مورد استفاده از نمودار حبابی پراکنش نگاشت جمعیت در مقابل مساحت کشورها می باشد. مثلا برای جدول زیر که سه متغیر برای هر کشور بررسی شده می توان نمودار حبابی رسم کرد.
نمودار راداری
استفاده از نمودار راداری روشی برای نمایش داده های چندمتغیره در قالب نموداری دو بعدی است که در آن سه متغیر کمی یا بیشتر بر روی محورهایی نشان داده می شوند که نقطه شروع همه آنها یکی است. محل قرارگیری و زاویه محورها نسبت به یکدیگر هیچ اطلاعات خاصی را بیان نمی کند.
- نمودار راداری از چند نیم خط به شکل پره های چرخ دوچرخه تشکیل می شود که در نقطه مرکزی به یکدیگر اتصال دارند و با زاویه های یکسان بین هم، گرداگرد آن نقطه قرار گرفته اند. هر کدام از این خطوط در واقع یک محور و نشان دهنده یک متغیر است پس می تواند درجه بندی شود به این خطوط اصطلاحا شعاع های نمودار راداری می گویند.
- اگر درجه بندی شعاع ها به گونه ای انجام گیرد که فاصله ی بین نشانک های متوالی بر روی همه ی شعاع ها یکسان باشد می توان خطوط راهنمای مقادیر را هم رسم کرد به شرطی که باعث شلوغی ِ نمودار نشود.
- گاهی این خطوط راهنما را به جای خط راست به صورت خط خم و دایره رسم می کنند در این حالت نمودار واقعا شبیه صفحه نمایش رادار می شود.
- نسبت مقدار یک متغیر، برای یک مشاهده به بیشینه ٔ آن متغیر به ازای همه ی مشاهده ها اندازه ی آن مقدار روی شعاع مربوط را مشخص می کند. این کار را برای همه متغیرها و بر روی همه ی شعاع ها انجام می دهیم. سپس نقاط مشخص شده روی شعاع های مجاور به ازای هر مشاهده را به هم وصل می کنیم. به این ترتیب، نمودار راداری برای یک مشاهده به دست خواهد آمد. اگر نمودار مربوط به دو یا چند مشاهده را روی هم بیندازیم، می توانیم مشاهده ها را با هم مقایسه کنیم.
- از این نمودار در ورزش برای نشان دادن میزان قدرت و ضعف بازیکنان نسبت به یکدیگر استفاده می شود.
نمودار راداری برای مقایسه چند مشاهده که متغیرهای یکسانی دارد مناسب است. یعنی اگر نمودار دو یا چند مشاهده را به صورت راداری رسم کرده و روی هم بیندازیم می توانیم آنها را باهم مقایسه کنیم و پاسخ سؤالهای زیر را به دست آوریم:
+کدام مشاهده ها شبیه به یکدیگرند؟
+ آیا داده دورافتادهای وجود دارد؟
+ مقدار کدام متغیر برای یک مشاهده نسبت به متغیرهای دیگر بیشتر یا کمتر است؟
+ مقدار کدام متغیر برای یک مشاهده نسبت به مشاهده های دیگر بیشتر یا کمتر است؟
+در نمودار راداری زاویه بین شعاع ها چه چیزی را نشان می دهد؟ اگر زاویه ها یکسان باشند می توان از روی آن تعداد متغیرها را تعیین کرد و اطلاعات دیگری نمی دهد.
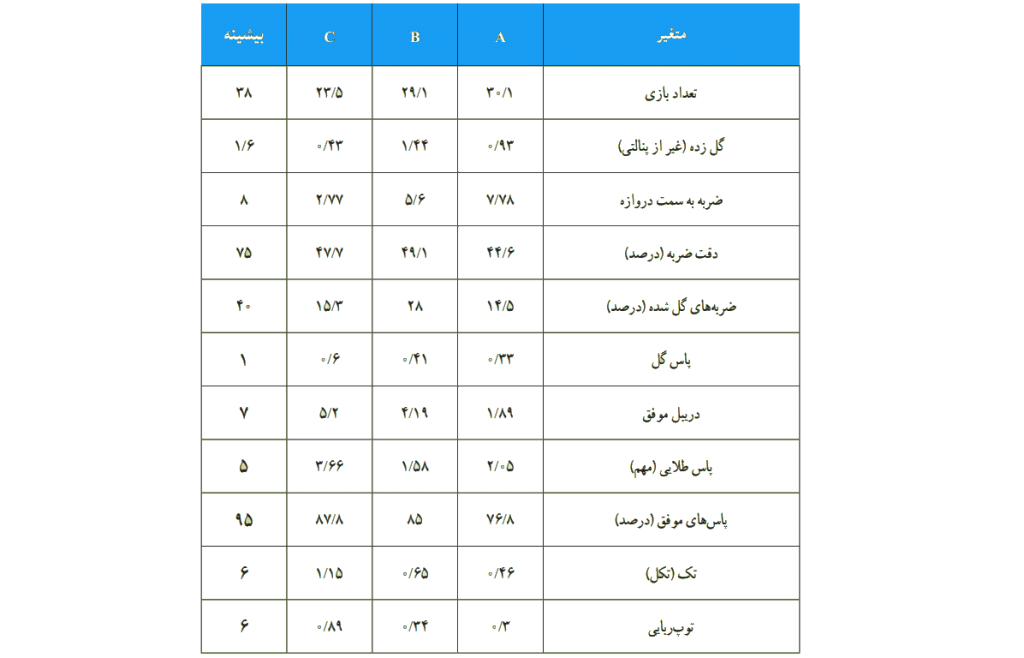
مثال: مثلا نامزدهای دریافت جایزه توپ طلا سه نفر بودند و
و
. عملکرد این سه بازیکن در جدول زیر آورده شده است.
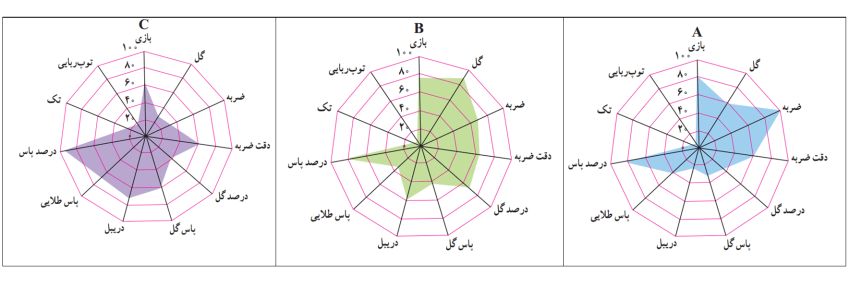
برای مقایسه این سه بازیکن ابتدا نمودار راداری هر کدام را به صورت زیر رسم می کنیم. برای این کار امتیاز هر بازیکن در هر موضوع را بر مقدار ماکزیمم امتیازی که می توانستند در آن موضوع بگیرند تقسیم کرده و عدد حاصل را در صد ضرب می کنیم به این ترتیب درصد عملکرد بازیکن برای هر موضوع بدست می آید. به تعداد موضوعات مطرح شده شاخه هایی یک اندازه با ترجیحا زوایای یکسان رسم می کنیم در نهایت با توجه به درصد عملکرد بازیکن نمودار آبی را برای او رسم می کنیم به همین ترتیب این کار را برای دو بازیکن دیگر انجام می دهیم تا سه شکل زیر بدست آید:
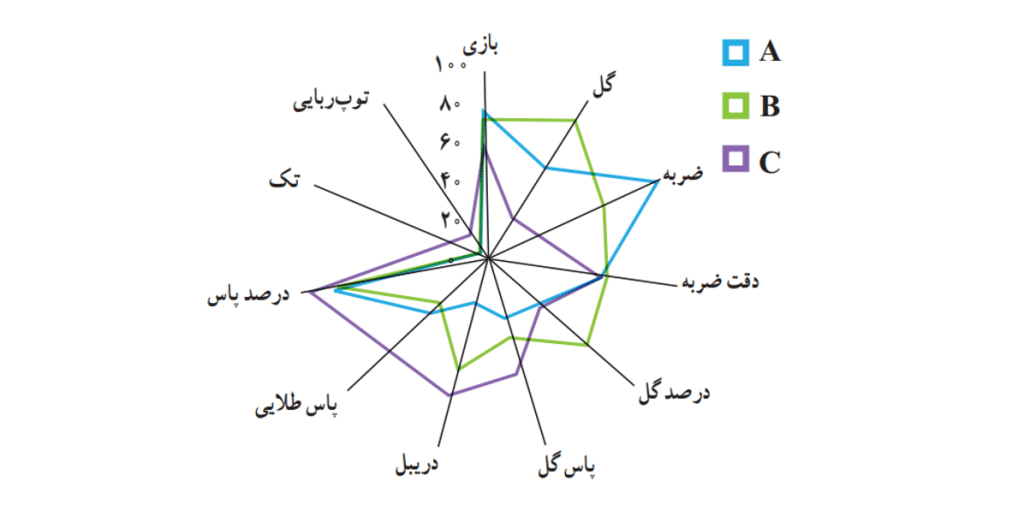
اگر این سه نمودار رنگی را روی هم بیندازیم متوجه می شویم در کل کدام بازیکن عملکرد بهتری داشته است. در شکل زیر این کار را انجام دادیم که متوجه می شویم بازیکن در کل وضعیت بهتری داشته است.
جمع بندی
در این مقاله توضیح جامعی در مورد نحوه رسم جدول فراوانی و دسته بندی داده ها بیان شده همچنین به طور کامل در مورد هر کدام از نمودار های آماری مانند نمودار میله ای یا ستونی، نمودار مستطیلی یا هیستوگرام، نمودار خط شکسته، نمودار دایره ای، نمودار حبابی و نمودار راداری توضیح جامعی همراه با مثال داده شده است که در متن مقاله می توانید آنها را مطالعه کنید. اگر علاقمند به دانستن تعریف اصطلاحات آماری، یادگیری در مورد شاخص های مرکزی و شاخص های پراکندگی می توانید به هر کدام از این مقاله ها مراجعه کنید. امیدواریم از خواندن این مقاله لذت و استفاده کافی برده باشید. لطفا ما را از نظرات خود در مورد مقاله جدول فراوانی و نمودارهای آماری در قسمت کامنت ها بهره مند کنید.

2 پاسخ
جدول فراوانی و همه نمودار ها رو یاد گرفتم اما هر چی تو کتاب ها گشتم نمودار راداری و حبابی رو ندیدم یعنی اسم همه بود غیر از این دو تا
برای دانشگاهه؟ چه رشته ای ؟
بله عزیزم همه نمودار های آمده در کتاب های هر سه رشته ریاضی و تجربی و انسانی در این مقاله تدریس شده . نمودار حبابی و رادارای برای پایه دهم رشته انسانی هست نه دو رشته دیگه احتمالا شما رشته ات انسانی نیست که نتونستی این دو نمودار رو در کتاب هات پیدا کنی