جامع ترین آموزش درباره روابط بین نسبت های مثلثاتی(مکمل، متمم، مجموع و تفاضل)

روابط بین نسبت های مثلثاتی فرمول هایی برای ساده سازی عبارت های مثلثاتی هستند که در حل معادلات مثلثاتی و بدست آوردن نسبت های مثلثاتی به ما کمک می کنند. روابط بین سینوس، کسینوس تانژانت و کتانژانت و همچنین نسب های دو زاویه متمم، قرینه، مکمل و … رابطه شیب خط با تانژانت و بدست آوردن مساحت مثلث با کمک نسبت های مثلثاتی همه و همه به طور کامل و جامع در این مقاله بیان شده است.

بین نسبت های مثلثاتی چه روابطی برقرار است؟

برای اینکه روابط بین نسبت های مثلثاتی را بدست آوریم باید چند نکته را بدانیم.

توجه: حاصل ضرب سینوس یک زاویه در خودش را به صورت زیر نشان می دهیم:

$\sin{\theta}\times \sin{\theta}=(\sin{\theta})^{2}=\sin^{2}{\theta}$

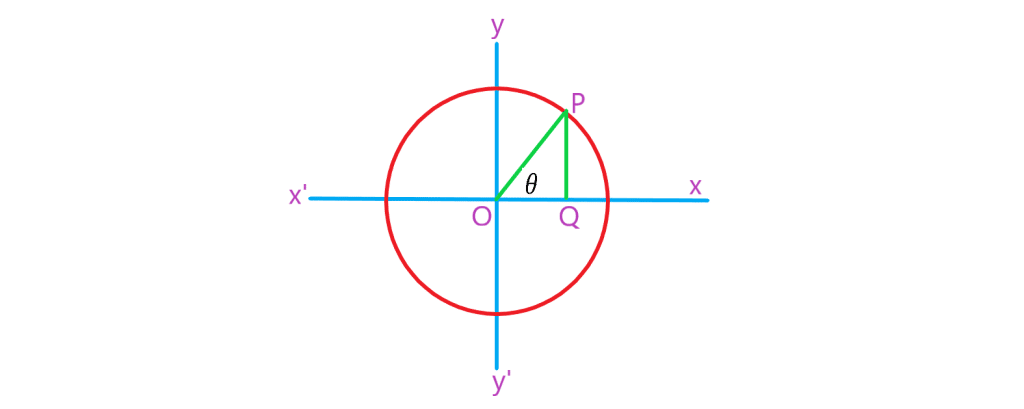
در دایره مثلثاتی زیر ( که در مقاله نسبت های مثلثاتی در مورد آن آموزش دیدیم) یک مثلث قائم الزاویه با عمود رسم کردن از نقطه $P$ بر محور طول ایجاد شده است. با توجه به اینکه $OPQ$ یک مثلث قائم الزاویه است می توان قضیه فیثاغورس را برای آن نوشت پس داریم:

$OQ^{2}+PQ^{2}=OP^{2}$

با توجه به اینکه در دایره مثلثاتی داریم: $OP=1$

و $PQ=\sin{\theta}$

و $OQ=\cos{\theta}$

بنابراین داریم:

$\sin^{2}{\theta}+\cos^{2}{\theta}=1$

نکته: با توجه به رابطه

$\sin^{2}{\theta}+\cos^{2}{\theta}=1$

اگر $\cos{\theta}$

را داشتیم و می خواستیم $\sin{\theta}$

را بدست آوریم از رابطه ی

$\sin{\theta}=\pm \sqrt{1-\cos^{2}{\theta}}$

و اگر $\sin{\theta}$

را داشتیم و می خواستیم $\cos{\theta}$

را بدست آوریم از رابطه ی

$\cos{\theta}=\pm \sqrt{1-\sin^{2}{\theta}}$

استفاده می کنیم. اینکه کدام علامت را در نظر بگیریم بستگی به اطلاعات سوال در مورد ناحیه زاویه $\theta$

دارد.

نکته : روابط زیر نیز برای نسبت های مثلثاتی زاویه دلخواه $\theta$ برقرار است:

$1+\tan^{2}{\theta}=\frac{1}{\cos^{2}{\theta}}\,\,\,\,,\,\,\,\,\cos{\theta}\neq 0$

$1+\cot^{2}{\theta}=\frac{1}{\sin^{2}{\theta}}\,\,\,\,,\,\,\,\,\sin{\theta}\neq 0$

$(1-\sin{\theta})(1+\sin{\theta})=1-\sin^{2}{\theta}=\cos^{2}{\theta}$

$\sin^{4}{\theta}-\cos^{4}{\theta}=\sin^{2}{\theta}-\cos^{2}{\theta}$

$\sin^{4}{\theta}+\cos^{4}{\theta}=1-2\sin^{2}{\theta}\cos^{2}{\theta}$

$\frac{1}{\cos{\theta}}+\cot{\theta}=\frac{\tan{\theta}+\cos{\theta}}{\sin{\theta}}$

$\frac{1+\tan{\theta}}{1+\cot{\theta}}=\tan{\theta}$

مثال: اگر کسینوس یک زاویه برابر با $\frac{3}{7}$ باشد و زاویه در ناحیه چهارم مختصات قرار داشته باشد سایر نسبت های مثلثاتی را بدست آورید؟

جواب:

$\cos{\theta}=\frac{3}{7}\,\rightarrow\,\,\sin^{2}{\theta}+\cos^{2}{\theta}=1$

$\rightarrow \,\sin^{2}{\theta}=1-\cos^{2}{\theta}=1-\frac{9}{49}=\frac{40}{49}$

$\rightarrow \,\,\,\, \sin{\theta}=\pm \frac{2\sqrt{10}}{7}$

$\overset{\theta \,\,\text{in 4th coordinate region}}{\rightarrow} \,\,\,\,\sin{\theta}=\frac{-2\sqrt{10}}{7}$

مثال: ثابت کنید تساوی های زیر اتحادند. (درستی هر یک از تساوی های زیر را بررسی کنید)

$\frac{1+\tan{\alpha}}{1+\cot{\alpha}}=\tan{\alpha}$

$1-\frac{cos^{2}{\alpha}}{1+\sin{\alpha}}=\sin{\alpha}$

$\frac{1}{\cos{\alpha}}-\tan{\alpha}=\frac{\cos{\alpha}}{1+\sin{\alpha}}$

جواب: با توجه به روابط مثلثاتی که در بالاتر بیان شده در هر مورد از یک سمت تساوی شروع می کنیم وبه سمت دیگر تساوی می رسیم. به این ترتیب هر کدام از این سه مورد اثبات می شود.

$\frac{1+\tan{\alpha}}{1+\cot{\alpha}}=$

$\frac{1+\frac{\sin{\alpha}}{\cos{\alpha}}}{1+\frac{\cos{\alpha}}{\sin{\alpha}}}$

$=\frac{\frac{\cos{\alpha}}{\cos{\alpha}}+\frac{\sin{\alpha}}{\cos{\alpha}}}{\frac{\sin{\alpha}}{\sin{\alpha}}+\frac{\cos{\alpha}}{\sin{\alpha}}}$

$=\frac{\frac{\cos{a}+\sin{a}}{\cos{a}}}{\frac{\cos{a}+\sin{a}}{\sin{a}}}$

$=\frac{\sin{\alpha}(\cos{\alpha}+\sin{\alpha})}{\cos{\alpha}(\cos{\alpha}+\sin{\alpha})}$

$=\frac{\sin{\alpha}}{\cos{\alpha}}=\tan{\alpha}$

$1-\frac{\cos^{2}{\alpha}}{1+\sin{\alpha}}=$

$\frac{1+\sin{\alpha}}{1+\sin{\alpha}}-\frac{\cos^{2}{\alpha}}{1+\sin{\alpha}}$

$=\frac{1+\sin{\alpha}-\cos^{2}{\alpha}}{1+\sin{\alpha}}$

$=\frac{1-\cos^{2}{\alpha}+\sin{\alpha}}{1+\sin{\alpha}}$

$=\frac{\sin^{2}{\alpha}+\sin{\alpha}}{1+\sin{\alpha}}$

$=\frac{\sin{\alpha}(1+\sin{\alpha})}{1+\sin{\alpha}}=\sin{\alpha}$

$\frac{1}{\cos{\theta}}-\tan{\theta}$

$=\frac{1}{\cos{\theta}}-\frac{\sin{\theta}}{\cos{\theta}}$

$=\frac{1-\sin{\theta}}{\cos{\theta}}\times \frac{1+\sin{\theta }}{1+\sin{\theta }}$

$=\frac{1-\sin^{2}{\theta}}{\cos{\theta}(1+\sin{\theta})}$

$=\frac{\cos^{2}{\theta}}{\cos{\theta}(1+\sin{\theta})}$

$=\frac{\cos{\theta}}{1+\sin{\theta}}$

نسبت های مثلثاتی دو زاویه متمم چه رابطه ای با هم دارند؟

به هر دو زاویه ای که مجموع زوایای آنها 90 درجه باشد متمم می گویند. رابطه بین نسبت های مثلثاتی دو زاویه متمم به صورت زیر است:

$\sin{(\frac{\pi}{2}-\theta)}=\cos{\theta}$

$\cos{(\frac{\pi}{2}-\theta)}=\sin{\theta}$

$\tan{(\frac{\pi}{2}-\theta)}=\cot{\theta}$

$\cot{(\frac{\pi}{2}-\theta)}=\tan{\theta}$

مثلا اگر بخواهیم نسبت های مثلثاتی زاویه 60 درجه را از روی زاویه 30 درجه ( جمع این دو زاویه با هم 90 درجه اند پس با هم متمم اند) می توانیم از روابط بالا استفاده کنیم:

$\sin{(\frac{\pi}{2}-30)}=\cos{30}=\frac{\sqrt{3}}{2}$

$\cos{(\frac{\pi}{2}-30)}=\sin{30}=\frac{1}{2}$

$\tan{(\frac{\pi}{2}-30)}=\cot{30 }=\sqrt{3}$

$\cot{(\frac{\pi}{2}-30)}=\tan{30}=\frac{\sqrt{3}}{3}$

در نتیجه مقادیر زاویه 60 درجه برابر است با:

$\sin{60}=\frac{\sqrt{3}}{2}\,\,\,,\,\,\,\cos{60}=\frac{1}{2}$

$\tan{60}=\sqrt{3}\,\,\,,\,\,\,\cot{60}=\frac{\sqrt{3}}{3}$

نسبت های مثلثاتی دو زاویه قرینه چه رابطه ای با هم دارند؟

دو زاویه $\theta$ و $-\theta$ قرینه یکدیگرند. رابطه ی بین نسبت های مثلثاتی دو زاویه قرینه به صورت زیر است:

$\sin{(-\theta)}=-\sin{(\theta)}$

$\cos{(-\theta)}=\cos{(\theta)}$

$\tan{(-\theta)}=-\tan{\theta}$

$\cot{(-\theta)}=-\cot{(\theta)}$

مثلا اگر بخواهیم اندازه نسبت های مثلثاتی زاویه $-30$ درجه را به کمک زاویه $30$ درجه بدست آوریم از فرمول های بالا استفاده می کنیم.

$\sin{(-30)}=-\sin{(30)}=\frac{-1}{2}$

$\cos{(-30)}=\cos{(30)}=\frac{\sqrt{3}}{2}$

$\tan{(-30)}=-\tan{(30)}=\frac{-\sqrt{3}}{3}$

$\cot{(-30)}=-\cot{(30)}=-\sqrt{3}$

نسبت های مثلثاتی دو زاویه مکمل چه رابطه ای با هم دارند؟

دو زاویه را مکمل می گوییم اگر مجموع آنها 180 درجه باشد. رابطه ی بین نسبت های مثلثاتی دو زاویه مکمل به صورت زیر است:

$\sin{(\pi-\theta)}=\sin{(\theta)}$

$\cos{(\pi-\theta)}=-\cos{(\theta)}$

$\tan{(\pi-\theta)}=-\tan{(\theta)}$

$\cot{(\pi-\theta)}=-\cot{(\theta)}$

مثلا اگر بخواهیم نسبت های مثلثاتی زاویه 120 درجه را از روی زاویه 60 درجه ( این دو زاویه با هم 180 درجه اند پس با هم مکمل اند) می توانیم از روابط بالا استفاده کنیم:

$\sin{(\pi-60)}=\sin{(60)}=\frac{\sqrt{3}}{2}$

$\cos{(\pi-60)}=-\cos{(60)}=-\frac{1}{2}$

$\tan{(\pi-60)}=-\tan{(60)}=-\sqrt{3}$

$\cot{(\pi-60)}=-\cot{(60)}=-\frac{\sqrt{3}}{3}$

نسبت های مثلثاتی با اختلاف ضرایب مختلفی از عدد پی

نسبت های مثلثاتی دو زاویه با اختلاف $\pi$

رابطه بین نسبت های مثلثاتی دو زاویه با اختلاف 180 درجه یا $\pi$ به صورت زیر است:

$\sin{(\pi+\theta)}=-\sin{(\theta)}$

$\cos{(\pi+\theta)}=-\cos{(\theta)}$

$\tan{(\pi+\theta)}=\tan{(\theta)}$

$\cot{(\pi+\theta)}=\cot{(\theta)}$

مثلا اگر بخواهیم با کمک زاویه 60 درجه اندازه نسبت های مثلثاتی زاویه 240 را بدست آوریم می توانیم از روابط مثلثاتی بالا استفاده کنیم. چون این دو زاویه با هم اختلاف 180 درجه دارند:

$\sin{(\pi+60)}=-\sin{(60)}=-\frac{\sqrt{3}}{2}$

$\cos{(\pi+60)}=-\cos{(60)}=-\frac{1}{2}$

$\tan{(\pi+60)}=\tan{(60)}=\sqrt{3}$

$\cot{(\pi+60)}=\cot{(60)}=\frac{\sqrt{3}}{3}$

نسبت های مثلثاتی دو زاویه با اختلاف $\frac{\pi}{2}$

رابطه بین نسبت های مثلثاتی دو زاویه با اختلاف 90 درجه به صورت زیر است:

$\sin{(\frac{\pi}{2}+\theta)}=\cos{(\theta)}$

$\cos{(\frac{\pi}{2}+\theta)}=-\sin{(\theta)}$

$\tan{(\frac{\pi}{2}+\theta)}=-\cot{(\theta)}$

$\cot{(\frac{\pi}{2}+\theta)}=-\tan{(\theta)}$

رابطه بین نسبت های مثلثاتی دو زاویه با اختلاف $2k\pi$ درجه به صورت زیر است:

$\sin{(2\pi+\theta)}=\sin{(\theta)}$

$\cos{(2\pi+\theta)}=\cos{(\theta)}$

$\tan{(2\pi+\theta)}=\tan{(\theta)}$

$\cot{(2\pi+\theta)}=\cot{(\theta)}$

$\sin{(2k\pi+\theta)}=\sin{(\theta)}$

$\cos{(2k\pi+\theta)}=\cos{(\theta)}$

$\tan{(2k\pi+\theta)}=\tan{(\theta)}$

$\cot{(2k\pi+\theta)}=\cot{(\theta)}$

رابطه بین نسبت های مثلثاتی دو زاویه که مجموع آنها $2k\pi$ درجه است به صورت زیر است:

$\sin{(2k\pi-\theta)}=-\sin{(\theta)}$

$\cos{(2k\pi-\theta)}=\cos{(\theta)}$

$\tan{(2k\pi-\theta)}=-\tan{(\theta)}$

$\cot{(2k\pi-\theta)}=-\cot{(\theta)}$

نسبت های مثلثاتی مجموع و تفاضل دو زاویه چه رابطه ای با نسبت های مثلثاتی دو زاویه دارد؟

روابط مثلثاتی دو برابر کمان را با کمک فرمول های زیر بدست می آوریم:

$\sin{2\alpha}=2\sin{\alpha}\cos{\alpha}$

$\cos{2\alpha}=cos^{2}{\alpha}-\sin^{2}{\alpha}$

$\cos{2\alpha}=1-2\sin^{2}{\alpha}$

$\cos{2\alpha}=2\cos^{2}{\alpha}-1$

روابط مثلثاتی مجموع دو زاویه را با توجه به نسبت های مثلثاتی هر کدام از زوایا را با کمک فرمول های زیر بدست می آوریم:

$\sin{(\alpha+\beta)}=\sin{\alpha}\cos{\beta}+\cos{\alpha}\sin{\beta}$

$\cos{(\alpha+\beta)}=\cos{\alpha}\cos{\beta}-\sin{\alpha}\sin{\beta}$

$\tan{(\alpha+\beta)}=\frac{\tan{\alpha}+\tan{\beta}}{1-\tan{\alpha}\tan{\beta}}$

روابط مثلثاتی اختلاف یا تفاضل دو زاویه را با توجه به نسبت های مثلثاتی هر کدام از زوایا را با کمک فرمول های زیر بدست می آوریم:

$\sin{(\alpha-\beta)}=\sin{\alpha}\cos{\beta}-\cos{\alpha}\sin{\beta}$

$\cos{(\alpha-\beta)}=\cos{\alpha}\cos{\beta}+\sin{\alpha}\sin{\beta}$

$\tan{(\alpha-\beta)}=\frac{\tan{\alpha}-\tan{\beta}}{1+\tan{\alpha}\tan{\beta}}$

دانستن روابط بین نسبت های مثلثاتی چه کاربردهایی در مباحث دیگر ریاضی دارد؟

در ادامه کاربرد نسبت های مثلثاتی را در هندسه و تابع خطی می بینیم:

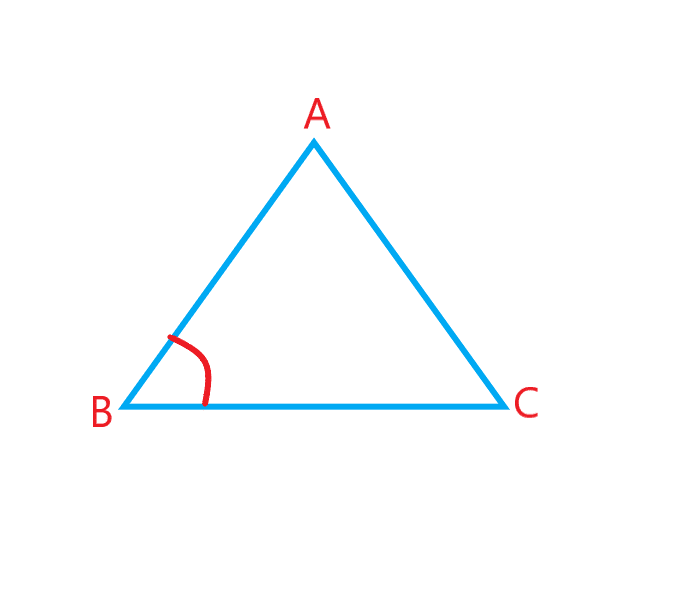
اندازه مساحت مثلث با کمک نسبت های مثلثاتی :

می دانیم مساحت مثلث برابر نصف حاصل ضرب قاعده در ارتفاع است اما با کمک علم مثلثات می توان از راه دیگری هم مساحت مثلث را بدست آورد مساحت مثلث برابر است با نصف حاصل ضرب دو ضلع در سینوس زاویه بین آنها. می توانیم بنویسیم:

$S=\frac{1}{2}AB\times BC \times \sin{B}$

رابطه شیب خط با تانژانت زاویه

شیب هر خط که محور افقی مختصات را قطع می کند، برابر است با تانژانت زاویه بین آن خط و جهت مثبت محور افقی. به عبارت دیگر، اگر $\alpha$ زاویه ای باشد که خط با جهت مثبت محور افقی می سازد، آنگاه شیب خط برابر با تانژانت زاویه $\alpha$ است.

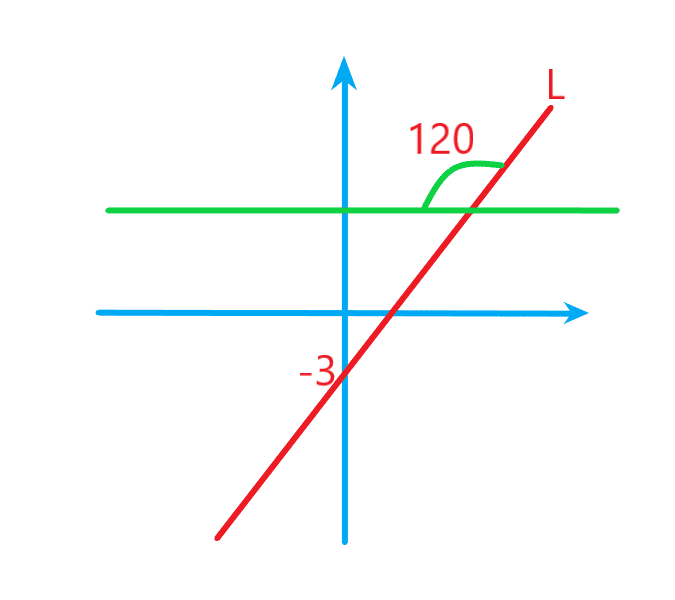
مثال: معادله خط زیر را بنویسید؟

طبق شکل عرض از مبدا برابر منفی سه است. زاویه بین خط و سمت راست محور طول برابر 60 درجه است چون $180-120=60$ . در نتیجه معادله خط به صورت زیر بدست می آید.

$\tan{60}=\sqrt{3}\,\,\,\,\rightarrow\,\,\,\,y=\sqrt{3}x-3$

همه ی فرمول های مربوط به روابط نسبت های مثلثاتی را به صورت خلاصه می توانید در جدول های زیر ببینید:

جمع بندی

در این مقاله روابط بین نسبت های مثلثاتی و فرمول های مربوط به آن را بیان کردیم همچنین نسبت های مثلثاتی مجموع و تفاضل دو زاویه، دو زاویه قرینه، دو زاویه متمم، دو زاویه مکمل را بیان کردیم. کاربرد روابط مثلثاتی در مسائل هندسی و معادله خط بیان شده است. اگر نیاز به اطلاعات پایه در مورد تعریف نسبت های مثلثاتی دارید به مقاله مربوطه مراجعه کنید. اگر می خواهید علم خود را در مورد مثلثات افزایش دهید به مقالات معادله مثلثاتی و نمودار و توابع مثلثاتی مراجعه کنید. لطفا نظرات خود را در مورد مقاله روابط بین نسبت های مثلثاتی را در قسمت کامنت ها بیان کنید.

2 پاسخ

فاطمه گفت:

آوریل 16, 2025 در 07:24

مرسی که فرمول ها و محاسبات رو پشت سر هم نمی نویسید آدم می فهمه چی می گید و البته بابت مقاله کامل تون و جدول های مفید تون خیلی ممنونم من از تیر ماه باید برای کنکور شروع کنم
اتفاقی با سایت فرامث آشنا شدم بابت این آشنایی خیلییییی خدا رو شاکرم

پاسخ
1. ریحانه حسینی گفت:
  
  آوریل 16, 2025 در 17:09
  
  ممنونم از تیزبینی و توجهت. امیدوارم موفق و سلامت باشی عزیزم ما هم خوشحالیم از اینکه کاربر با دقت و تیزبینی مثل تو داریم عزیزم
  
  پاسخ

جامع ترین آموزش درباره روابط بین نسبت های مثلثاتی(مکمل، متمم، مجموع و تفاضل)

بین نسبت های مثلثاتی چه روابطی برقرار است؟

نسبت های مثلثاتی دو زاویه متمم چه رابطه ای با هم دارند؟

نسبت های مثلثاتی دو زاویه قرینه چه رابطه ای با هم دارند؟

نسبت های مثلثاتی دو زاویه مکمل چه رابطه ای با هم دارند؟

نسبت های مثلثاتی با اختلاف ضرایب مختلفی از عدد پی

نسبت های مثلثاتی مجموع و تفاضل دو زاویه چه رابطه ای با نسبت های مثلثاتی دو زاویه دارد؟

دانستن روابط بین نسبت های مثلثاتی چه کاربردهایی در مباحث دیگر ریاضی دارد؟

2 پاسخ

دیدگاهتان را بنویسید لغو پاسخ

آخرین مطالب وبلاگ

دنباله های عددی

تابع خطی و معادله خط

تابع و دامنه و برد آن

تعیین علامت

عبارت و معادله گویا

معادله درجه دوم

معادله

عبارت جبری

قدرمطلق

دوره ها

دسترسی سریع

دسترسی سریع

مقالات مادر