جامع ترین آموزش درباره حل انواع معادلات مثلثاتی (سینوسی، کسینوسی، تانژانتی)

معادله مثلثاتی معادله ای است که در آن اطلاعاتی از نسبت های مثلثاتی یک زاویه مجهول داریم و باید زاویه هایی که در آن معادله صدق می کنند را بیابیم تا معادله مثلثاتی را حل کرده باشیم. برای اینکه بتوانیم به طور کلی همه ی معادلات مثلثاتی را حل کنیم و زوایایی که در معادله مورد نظر صدق می کنند را پیدا کنیم به دو پیش نیاز نیازمندیم. یکی اینکه باید روابط مثلثاتی را بدانیم که در مقاله روابط بین نسبت های مثلثاتی درباره آن خوانده اید. دوم اینکه یک سری قوانین مشخص برای حل معادلات بدانیم. در این مقاله به آموزش مورد دوم می پردازیم قوانین حل برخی از معادلات را در این مقاله آموزش می دهیم. با ما در این مقاله همراه باشید.

چطور یک معادله ی سینوسی را حل کنیم؟

یکی از انواع معادلات مثلثاتی، معادلات سینوسی هستند. اگر معادله ای به صورت $\sin{x}=\sin{\alpha}$ داشته باشیم و $\alpha$ زاویه ای معلوم باشد آنگاه زاویه ی مجهول $x$ به صورت زیر بدست می آید .

$\begin{cases}x=2k\pi+\alpha \\ x=(2k+1)\pi-\alpha \end{cases} \,\,\,\,\,\,,k \in \Bbb{Z}$

مثال: جواب های معادله $\sin{x}=\frac{1}{2}$ در بازه ی $[-\pi,\pi]$ پیدا کنید.

جواب: برای حل معادله ی $\sin{x}=\frac{1}{2}$ با توجه به آنچه در مقاله تعریف نسبت های مثلثاتی و روابط نسبت مثلثاتی زوایا خواندیم می نویسیم $\sin{\frac{\pi}{6}}=\frac{1}{2}$ . حالا می توانیم معادله $\sin{x}=\frac{1}{2}$ را به صورت $\sin{x}=\sin{\frac{\pi}{6}}$ بنویسیم. در گام سوم باید بنویسیم:

$\begin{cases}x=2k\pi+\frac{\pi}{6} \\ x=(2k+1)\pi-\frac{\pi}{6} \end{cases} \,\,\,\,\,\,,k \in \Bbb{Z}$

در گام آخر به جای $k$ اعداد صحیح مختلف قرار می دهیم تا $x$ هایی در بازه ی خواسته شده ی صورت سوال یعنی $[-\pi,\pi]$ پیدا کنیم:

$k=0\rightarrow\begin{cases}x= +\frac{\pi}{6} \\ x=\pi-\frac{\pi}{6}=\frac{5\pi}{6} \end{cases}$

$k=1\rightarrow \begin{cases}x= 2\pi+\frac{\pi}{6} > \pi \\ x=3\pi-\frac{\pi}{6}=\frac{17\pi}{6} > \pi \end{cases}$

$k=-1\rightarrow\begin{cases}x= -2\pi+\frac{\pi}{6}=-\frac{11\pi}{6} < -\pi \\ x=-\pi-\frac{\pi}{6}=\frac{-7\pi}{6} < -\pi \end{cases}$

پس این معادله دو جواب دارد $x=+\frac{\pi}{6}$ و $x=\frac{5\pi}{6}$ که هر دو به ازای $k=0$ بدست می آیند.

چطور یک معادله کسینوسی را حل کنیم؟

یکی از انواع معادلات مثلثاتی، معادلات کسینوسی هستند. اگر معادله ای به صورت $\cos{x}=\cos{\alpha}$ داشته باشیم و $\alpha$ زاویه ای معلوم باشد آنگاه زاویه ی مجهول $x$ به صورت زیر بدست می آید.

$\begin{cases} x=2k\pi+\alpha \\ x=2k\pi-\alpha \end{cases}\,\,\,\,k \in \Bbb{Z}$

مثال: جواب های معادله $\cos{x}=\frac{1}{2}$ در بازه ی $[-\pi,\pi]$ پیدا کنید.

جواب: برای حل معادله ی $\cos{x}=\frac{1}{2}$ با توجه به آنچه در مقاله تعریف نسبت های مثلثاتی و روابط نسبت مثلثاتی زوایا خواندیم می نویسیم $\cos{\frac{\pi}{3}}=\frac{1}{2}$ . حالا می توانیم معادله $\cos{x}=\frac{1}{2}$ را به صورت $\cos{x}=\cos{\frac{\pi}{3}}$ بنویسیم. در گام سوم باید بنویسیم:

$\begin{cases} x=2k\pi+\frac{\pi}{3} \\ x=2k\pi-\frac{\pi}{3} \end{cases}\,\,\,\,k \in \Bbb{Z}$

$k=0 \rightarrow \begin{cases} x= +\frac{\pi}{3} \\ x= -\frac{\pi}{3} \end{cases}$

$k=1\rightarrow\begin{cases} x=2\pi +\frac{\pi}{3}=\frac{7\pi}{3} > \pi \\ x= 2\pi-\frac{\pi}{3}=\frac{5\pi}{3} > \pi \end{cases}$

$k=-1\rightarrow \begin{cases} x=-2\pi +\frac{\pi}{3}=-\frac{5\pi}{3} < -\pi \\ x= -2\pi-\frac{\pi}{3}=-\frac{7\pi}{3} < -\pi \end{cases}$

پس این معادله دو جواب دارد $x=+\frac{\pi}{3}$ و $x=-\frac{\pi}{3}$ که هر دو به ازای $k=0$ بدست می آیند.

چطور یک معادله تانژانتی را حل کنیم؟

یکی از انواع معادلات مثلثاتی، معادلات تانژانتی هستند. اگر معادله ای به صورت $\tan{x}=\tan{\alpha}$ داشته باشیم و $\alpha$ زاویه ای معلوم باشد آنگاه زاویه ی مجهول $x$ به صورت زیر بدست می آید.

$x=k\pi+\alpha\,\,\,\,,\,\,\,\,k \in \Bbb{Z}$

مثال: جواب های معادله $\tan{x}=\sqrt{3}$ را در بازه ی $[-\pi,\pi]$ پیدا کنید.

جواب: برای حل معادله ی $\tan{x}=\sqrt{3}$ با توجه به آنچه در مقاله نسبت های مثلثاتی و روابط نسبت مثلثاتی زوایا خواندیم می نویسیم $\tan{\frac{\pi}{3}}=\sqrt{3}$ . حالا می توانیم معادله $\tan{x}=\sqrt{3}$ را به صورت $\tan{x}=\tan{\frac{\pi}{3}}$ بنویسیم. در گام سوم باید بنویسیم $x=k\pi+\frac{\pi}{3}$ در گام آخر به جای $k$ اعداد صحیح مختلف قرار می دهیم تا $x$ هایی در بازه ی خواسته شده ی صورت سوال یعنی $[-\pi,\pi]$ پیدا کنیم:

$k=0\,\,\,\,\rightarrow\,\,\,\, x=+\frac{\pi}{3}$

$k=1\,\,\,\,\rightarrow\,\,\,\, x=\pi+\frac{\pi}{3}=\frac{4\pi}{3} > \pi$

$k=-1\,\,\,\,\rightarrow\,\,\,\, x=-\pi+\frac{\pi}{3}=-\frac{2\pi}{3}$

$k=-2\,\,\,\,\rightarrow\,\,\,\, x=-2\pi+\frac{\pi}{3}=-\frac{5\pi}{3} < -\pi$

پس این معادله دو جواب دارد $x=+\frac{\pi}{3}$ و $x=-\frac{2\pi}{3}$ که به ازای $k=0$ و $k=-1$ بدست می آیند.

در حالت کلی چطور یک معادله مثلثاتی را حل کنیم؟

در حالت کلی اگر یک معادله مثلثاتی به ما داده شده ابتدا باید با توجه به روابط نسبت های مثلثاتی آن معادله را تبدیل به معادلات سینوسی ، کسینوسی و تانژانتی که در این مقاله بیان شده تبدیل کنیم. سپس معادله جدید را با توجه به مطالب آموزش داده شده در این مقاله و آنچه در مقاله معرفی نسبت های مثلثاتی آموختیم حل کنیم.

مثال: معادلات زیر را حل کنید.

$1) \sin{\frac{\pi}{2}}=\sin{3x}$

$2) \cos^{2}{x}-\sin{x}=\frac{1}{4}$

$3) \cos{2x}-3\sin{x}+1=0$

$4) \cos{2x}-\cos{x}+1=0$

جواب: برای حل این معادلات ابتدا باید هر کدام را با توجه به روابط نسبت های مثلثاتی ساده کنیم تا بصورت معادلات معروف مثلثاتی که در این مقاله آموزش داده شده در بیایند.

$1)\sin{\frac{\pi}{2}}=\sin{3x}$

$\rightarrow\,\,\,\,\begin{cases} 3x=2k\pi+\frac{\pi}{2} \\ 3x=(2k+1)\pi-\frac{\pi}{2} \end{cases}$

$\rightarrow\,\,\,\begin{cases}x=\frac{2k\pi}{3}+\frac{\pi}{6} \\ x=\frac{(2k+1)\pi}{3}-\frac{\pi}{6} \end{cases}$

$2) \cos^{2}{x}-\sin{x}=\frac{1}{4}$

$\rightarrow \, 1-\sin^{2}{x}-\sin{x}=\frac{1}{4}$

$\rightarrow \,\sin^{2}{x}+\sin{x}-\frac{3}{4}=0$

حالا برای حل این معادله درجه دو که با کمک رابطه ی مثلثاتی $\sin^{2}{x}+\cos^{2}{x}=1$ بدست آمد از تغییر متغیر استفاده می کنیم به طوری که قرار می دهیم $\sin{x}=a$ . حالا معادله ی درجه دو یی داریم که با روش دلتا می توانیم آن را حل کنیم. البته فقط جواب هایی را از آن قبول می کنیم که بین $-1$ و $+1$ باشد. داریم:

$a^{2}+a-\frac{3}{4}=0$

$\rightarrow \Delta=1^{2}-4\times 1 \times (-\frac{3}{4})=4$

$\rightarrow \, a=\frac{-1\pm\sqrt{4}}{2\times 1}=\frac{-1\pm 2}{2}$

$\rightarrow\,\,\,\,a=\frac{-3}{2}\,\,,\,\,a=\frac{1}{2}$

که فقط جواب $a=\frac{1}{2}$ را قبول می کنیم که در نتیجه $\sin{x}=\frac{1}{2}$ . حالا باید طبق مطالب این مقاله در بخش معادلات سینوسی عمل کنیم.

$\sin{\frac{\pi}{6}}=\frac{1}{2}\rightarrow\sin{x}=\sin{\frac{\pi}{6}}$

$\rightarrow\,\,\,\,\begin{cases}x=2k\pi+\frac{\pi}{6} \\ x=(2k+1)\pi-\frac{\pi}{6}\end{cases}$

$3) \cos{2x}-3\sin{x}+1=0$

$\rightarrow 1-2\sin^{2}{x}-3\sin{x}+1=0$

$\rightarrow 2\sin^{2}{x}+3\sin{x}-2=0$

$\rightarrow \sin{x}=a\rightarrow 2a^{2}+3a-2=0$

$\rightarrow \Delta=3^{2}-4\times 2\times (-2)=25$

$\rightarrow \,a=\frac{-3\pm5}{4}\rightarrow a=-2\,\,,\,\,a=\frac{1}{2}$

$\sin{\frac{\pi}{6}}=\frac{1}{2}\rightarrow \sin{x}=\sin{\frac{\pi}{6}}$

$\rightarrow\begin{cases}x=2k\pi+\frac{\pi}{6} \\ x=(2k+1)\pi-\frac{\pi}{6}\end{cases}$

$4) \cos{2x}-\cos{x}+1=0$

$\rightarrow 2\cos^{2}{x}-1-\cos{x}+1=0$

$\rightarrow 2\cos^{2}{x}-\cos{x}=0$

$\rightarrow\,\,\,\,\cos{x}(2\cos{x}-1)=0$

چون حاصل ضرب دو عبارت صفر شد پس حتما یکی از آنها صفر است:

$\rightarrow \,\,\,\cos{x}=0$

$2\cos{x}-1=0\rightarrow\cos{x}=\frac{1}{2}$

حالا جواب هر کدام را بدست می آوریم

$\cos{x}=0=\cos{\frac{\pi}{2}}$

$\rightarrow \begin{cases}x=2k\pi+\frac{\pi}{2} \\x=2k\pi-\frac{\pi}{2}\end{cases}$

$\cos{x}=\frac{1}{2}=\cos{\frac{\pi}{3}}$

$\rightarrow\begin{cases}x=2k\pi+\frac{\pi}{3} \\x=2k\pi-\frac{\pi}{3}\end{cases}$

پس این معادله چهار دسته جواب دارد.

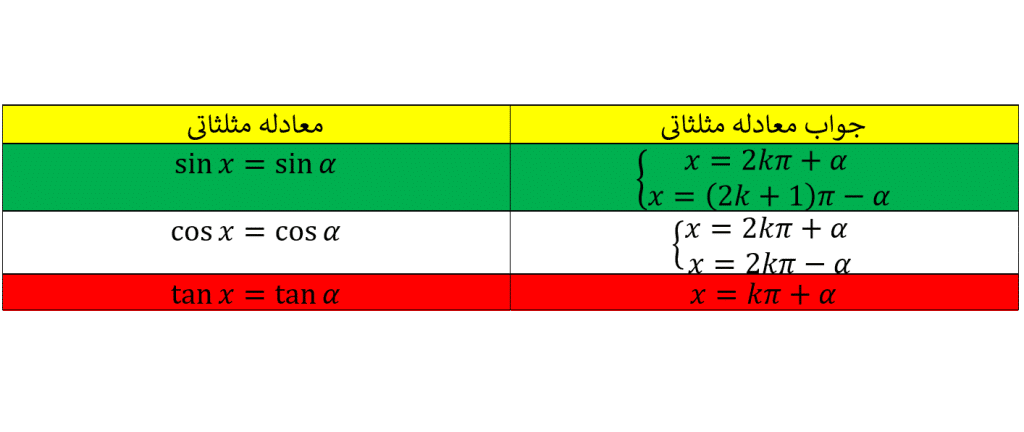
به پایان این مقاله جامع رسیدیم بعنوان برگه فرمول می توانید همه ی فرمول های معادلات مثلثاتی را می توانید در جدول زیر ببینید:

جمع بندی

در این مقاله به آموزش حل معادلات مثلثاتی به همراه مثال های زیادی پرداختیم. سه دسته بندی برای حل معادلات مثلثاتی انجام دادیم یعنی معادلات سینوسی ، معادلات کسینوسی ، معادلات تانژانتی. در واقع با کمک روابط مثلثاتی معادلات مثلثاتی را ساده می کنیم تا به یکی از سه دسته تبدیل شود و بعد از آن این معادلات را طبق دستورالعملی که برای هر معادله در مقاله ی معادلات مثلثاتی داده شده حل می کنیم. اگر به مطالعه در مورد توابع مثلثاتی و رسم نمودارهایشان نیاز دارید به مقاله مربوطه مراجعه کنید لطفا نظرات خود را در قسمت کامنت ها بیان کنید. امیدواریم از این آموزش جامع درباره ی معادلات مثلثاتی لذت برده باشید.

2 پاسخ

الهام گفت:

آوریل 16, 2025 در 07:26

مرسی از برگه فرمول جدولی
مرسی از کامل بودن و خلاصه بودن و
مرسی از مثال های مناسب

پاسخ
1. ریحانه حسینی گفت:
  
  آوریل 16, 2025 در 17:02
  
  سلامت باشی عزیزم خوشحالم برات مفید بوده
  
  پاسخ

جامع ترین آموزش درباره حل انواع معادلات مثلثاتی (سینوسی، کسینوسی، تانژانتی)

چطور یک معادله ی سینوسی را حل کنیم؟

چطور یک معادله کسینوسی را حل کنیم؟

چطور یک معادله تانژانتی را حل کنیم؟

در حالت کلی چطور یک معادله مثلثاتی را حل کنیم؟

2 پاسخ

دیدگاهتان را بنویسید لغو پاسخ

آخرین مطالب وبلاگ

دنباله های عددی

تابع خطی و معادله خط

تابع و دامنه و برد آن

تعیین علامت

عبارت و معادله گویا

معادله درجه دوم

معادله

عبارت جبری

قدرمطلق

دوره ها

دسترسی سریع

دسترسی سریع

مقالات مادر