جامع ترین آموزش حل معادله درجه دوم (تجزیه، مربع کامل کردن و روش کلی)
معادله درجه دوم یک بحث مهم برای همه ی علوم علی الخصوص علوم ریاضی و مهندسی است مثلا برای حل معادله گویا ، یا بدست آوردن نقاط برخورد تابع سهمی با محور طول ها، یا تعیین علامت یک عبارت شامل معادله درجه دوم، یا حل مسائل حد و مشتق نیاز به دانستن روش های حل معادله درجه دوم دارید. بنابراین اگر می خواهید همه چیز را درباره معادله درجه دوم بدانید هرگز این مقاله را از دست ندهید تا بتوانید روش های تجزیه (فاکتورگیری و اتحاد) که در مقاله عبارت جبری درباره آن خواندید ، مربع کامل کردن و روش کلی یا دلتا را به طور کامل بیاموزید.
چطور معادله درجه دوم را تشخیص دهیم؟
روش اول حل معادله درجه دوم: تجزیه ریشه گیری و اتحاد
این روش را با کمک ِ آنچه در مقاله جبر خواندیم انجام می دهیم البته این روش برای حل معادله درجه دو همیشه کاربرد ندارد یعنی نمی توان همه ی معادله های درجه دو را با این روش حل کرد. همانطور که قبلا اتحاد ها را خواندیم می دانیم چطور تشخیص دهیم یک عبارت جبری که در سمت چپ معادله درجه دو قرار دارد را به صورت یک اتحاد بنویسیم.
معادلات زیر به روش تجزیه حل شده اند:
روش دوم حل معادله درجه دوم: مربع کامل کردن
برای اینکه معادله درجه دوم را از طریق روش مربع کامل حل کنیم باید ابتدا عدد ثابت را به سمت راست تساوی ببریم سپس دو طرف تساوی را بر ضریب
یعنی
تقسیم کنیم بعد ضریب
را نصف کنیم و بعد آن را به توان دوم رسانده و به دو طرف تساوی اضافه کنیم در نهایت باید سمت چپ تساوی را به اتحاد مربع دو جمله ای تبدیل کرده و سمت راست تساوی را ساده کنیم در آخر با ریشه گیری کردن می توانیم به جواب معادله درجه دوم برسیم.
بدست می آید: که اگر عبارت زیر رادیکال منفی باشد، معادله جواب ندارد. اگر صفر باشد معادله درجه دو یک ریشه مضاعف دارد. اگر مثبت باشد معادله دو ریشه دارد.
مثال: معادله زیر به روش مربع کامل کردن حل شده است:
روش سوم حل معادله درجه سوم: روش کلی یا دلتا
روش کلی برای حل معادله درجه دو از رابطه ی
بدست می آید. عبارت
را مبین معادله درجه دوم می نامند و با
نشان می دهند.
اگر باشد معادله دارای دو جواب است که عبارتند از:
اگر باشد معادله دارای یک جواب است که به آن ریشه مضاعف می گویند:
اگر باشد معادله جواب ندارد.
مثال : معادله زیر به روش دلتا یا روش کلی حل شده است:
ریشه های معادله درجه دوم چه روابطی با هم دارند؟
جمع ریشه های یک معادله درجه دو (اگر معادله دو ریشه داشته باشد) با ضابطه برابر با
می باشد و حاصل ضرب ریشه ها برابر با
می باشد.
همچنین قدرمطلق تفاضل ریشه ها می باشد.
اگر ریشه های معادله درجه دوم
باشند داریم:
چند نکته درباره ریشه های معادله درجه دوم
نکته اول: در معادله درجه دوم اگر
باشد یکی از ریشه ها
و دیگری
می باشد.
اثبات:
نکته دوم: در معادله درجه دوم اگر
باشد یکی از ریشه ها
و دیگری
می باشد.
اثبات:
می توانید همه ی فرمول های مربوط به معادله درجه دوم و ریشه هایش را در جدول زیر ببینید:
جمع بندی
در این مقاله به آموزش تشخیص معادله درجه دوم و حل آن به سه روش پرداخته شد. سپس روابط بین ریشه های یک معادله درجه دوم به طور کامل بیان شد. مثال هایی هم برای آموزش هر روش حل معادله درجه دوم بیان شد. در نتیجه با خواندن این مقاله می توانید به راحتی مقالات معادله گویا، تعیین علامت، تابع، حد و مشتق بروید چرا که هر آنچه که از معادله درجه دوم نیاز است بدانید را از این مقاله آموخته اید. اگر تمایل دارید که به صورت جامع و بهمراه نمونه سوالات کنکور و نهایی در سالهای مختلف این مطالب را بیاموزید دوره جبر معادله تابع فرامث را تهیه کنید. لطفا نظرات ارزشمند خود را درباره ی مقاله معادله درجه دوم در قسمت کامنت ها بیان کنید.

![Rendered by QuickLaTeX.com \[\rightarrow\,\,\,\begin{cases} ax+c=0 \rightarrow x=\frac{-c}{a} \\ x+1=0\rightarrow x=-1 \end{cases}\]](https://faramath.com/core/ql-cache/quicklatex.com-6038231380bd4f80a3c320646d1a181f_l3.png)
![Rendered by QuickLaTeX.com \[\rightarrow \,\,\, \begin{cases} ax-c=0\rightarrow x=\frac{c}{a} \\ x-1=0\rightarrow x=1\end{cases}\]](https://faramath.com/core/ql-cache/quicklatex.com-05fb98d3e83c1858cfdd28fc449f3088_l3.png)
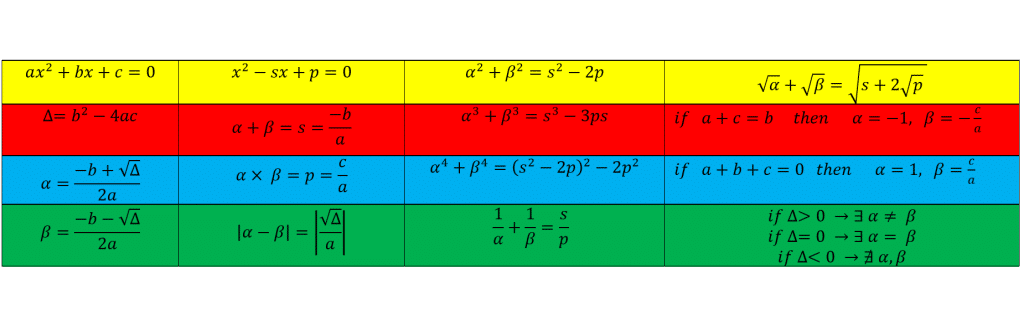

2 پاسخ
وای خدایا شکرت بالاخره یه مقاله پیدا کردم هر سه روش رو داشته باشه مرسیییییییی
خوشحالم که خوشحالی