همه چیز درباب قدرمطلق، توابع قدرمطلقی و رسم آنها، معادله و نامعادله قدرمطلقی

قدرمطلق با نماد $|x|$ یا نماد $abs()$ که برگرفته از ترجمه انگلیسی آن یعنی $Absolute-Value$ می باشد؛ در ماشین حساب نمایش داده می شود. قدر مطلق هر عدد به معنای فاصله ی آن عدد از عدد صفر است. در این مقاله به تعریف جامعی از قدرمطلق، ویژگی ها و خواص قدرمطلق، جمع و تفریق عبارات شامل قدرمطلق، رسم توابع قدرمطلقی، حل معادلات قدرمطلقی و حل نامعادلات قدرمطلقی می پردازیم. برای اینکه از این مقاله بهره کامل ببرید بهتر است قبل از آن مقالات مربوط به اعداد گنگ و اعداد حقیقی و مجموعه را مطالعه بفرمایید. امیدواریم خواندن این مقاله اطلاعات جامعی از این مبحث به شما بدهد.

تعریف قدرمطلق، چطور حاصل یک عبارت قدرمطلقی را بدست آوریم؟

فاصله نمایش عدد $a$ از مبدا مختصات را قدرمطلق $a$ می نامند و با علامت $|a|$ نشان می دهند. چون فاصله $2$ و $-2$ از مبدا برابر $2$ است پس می توان نوشت $|+2|=|-2|=2$ .

قدرمطلق عدد صفر و اعداد حقیقی مثبت برابر خودشان است اما قدرمطلق اعداد حقیقی منفی برابر قرینه شان است.

$|a|=\begin{cases}a&\,\,\,a\ge0\\-a&\,\,\,a<0\end{cases}$

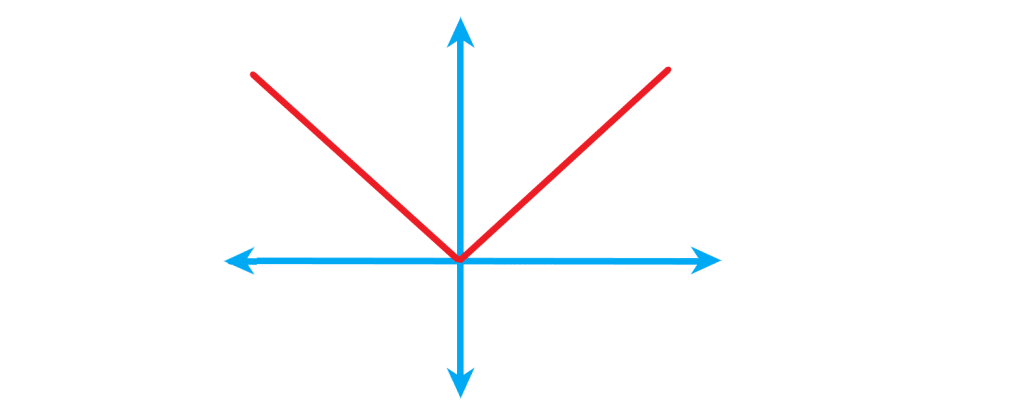
شکل تابع قدرمطلقی به صورت زیر است:

مثال: حاصل عبارت های زیر را بدست آورید:

$|-30|=30\,\,\,,\,\,\,|1.4|=1.4\,\,\,,\,\,\,|60.5|=60.5$

$|-0.7|=0.7\,\,\,,\,\,\,|-\frac{-6}{-8}|=\frac{6}{8}$

نکته : همانطور که در بخش اعداد گنگ خواندیم مقدار تقریبی رادیکال های زیر را برای اینکه بتوانیم تشخیص دهیم عدد داخل قدر مطلق مثبت است یا منفی باید بدانیم:

$\sqrt{2}\cong 1.4 \,\,\,, \,\,\, \sqrt{3}\cong 1.7$

$\sqrt{5}\cong 2.2\,\,\,,\,\,\,\sqrt{6}\cong 2.4$

$\sqrt{7}\cong 2.6\,\,\,,\,\,\,\sqrt{8}\cong 2.8$

مثال: حاصل قدرمطلق های زیر را بیابید؟

$|2-\sqrt{2} |=2-\sqrt{3} \,\,\,\,\,(2-1.7 >0)$

$|\sqrt{7}-2\sqrt{2} |=2\sqrt{2}-\sqrt{7}\,\,\,\,\,(2.6-2.8 < 0)$

$| -3-\sqrt{5}|=3+\sqrt{5} \,\,\,(-3-2.2 <0)$

نکته : با توجه به مفهوم قدرمطلق داریم: $\sqrt{a^{2}}=|a|$

مثال : حاصل عبارت ها را بدست آورید.

جواب: با توجه به نکته بالا حاصل رادیکال را به صورت قدرمطلق می نویسیم و با توجه به آنچه در مثال قبلی گفته شد برای بدست آوردن مقدار قدرمطلق باید مقدار تقریبی رادیکال ها را در نظر بگیریم. داریم:

$\sqrt{(1-\sqrt{2})^{2}}=|1-\sqrt{2}|=-1+\sqrt{2}$

$\sqrt{(\sqrt{7}-2\sqrt{2})^{2}}=|\sqrt{7}-2\sqrt{2}|=-\sqrt{7}+2\sqrt{2}$

$\sqrt{(\sqrt{8}-\sqrt{5})^{2}}=|\sqrt{8}-\sqrt{5}|=\sqrt{8}-\sqrt{5}$

ویژگی ها و خواص قدرمطلق چیست؟

قدرمطلق یک سری ویژگی ها با توجه به تعریفش دارد که به صورت زیر تعریف می شود:

همیشه قدرمطلق، عبارتی نا منفی است:

$| x| \ge 0$

ریشه دوم مجذورهر عبارتی برابر قدرمطلق آن عبارت است.

$\sqrt{x^{2}}=|x|$

اگر قدرمطلق یک عبارت برابر با یک عدد مثبت باشد. آن عبارت برابر با خود عدد یا قرینه آن می باشد.

$|x|=a\,\, \Leftrightarrow (x=a) \lor (x=-a) \,\, (a \ge 0)$

$|x|=|a| \,\,\Leftrightarrow (x=a) \lor (x=-a)$

مقدار قدرمطلق یک عدد با قدرمطلق قرینه آن عدد برابر است.

$|-x|=|x|$

مجذور یک عدد با مجذور قدرمطلق آن عدد برابر است.

$|x|^{2}=x^{2}$

حاصل ضرب قدرمطلق دو عدد با قدرمطلق حاصلضربشان برابر است

$|ab|=|a||b|$

حاصل تقسیم قدرمطلق دو عدد با قدرمطلق حاصل تقسیم شان برابر است.

$|\frac{a}{b}|=\frac{|a|}{|b|}$

هر عدد بین قدرمطلقش و قرینه قدرمطلقش قرار دارد چون حتما با یکی از این دو عبارت برابر است.

$\forall a,b \in \Bbb{R}\,\,\,\, -|a| \le a \le |a|$

برای حاصل جمع دو عبارت می توانیم به خواص قدرمطلقی زیر توجه کنیم:

$\forall a,b \in \Bbb{R}\,\,\,\, -|a|-|b| \le a+b \le |a|+|b|$

$\forall a,b \in \Bbb{R}\,\,\,\, |a+b| \le |a|+|b|$

مثال : با توجه به ویژگی های قدرمطلق داریم:

$\sqrt{(-7)^{2}}=|-7|=+7$

$|x|=5 \,\,\Leftrightarrow\,\, x=5 \lor x=-5$

$\forall x : |x|\neq -5$

$|x|=|-12|\,\,\Leftrightarrow \,\, x=-12 \lor x=+12$

$|-8|^{2}=(-8)^{2}\,\,\,,\,\,\, |+8|^{2}=(+8)^{2}$

$|8\times (-7)|=|8|\times |-7|=+56$

$|\frac{9}{-13}|=\frac{|9|}{|-13|}=\frac{9}{13}$

$|-25|=|25|=25$

نکته : در نامساوی های قدرمطلقی به نکات زیر توجه کنید. هر نامساوی یک بازه یا اجتماع چند بازه را نشان می دهد. (برای اطلاعات بیشتر راجع به بازه ها و عملِ اجتماع به مقاله اعداد حقیقی و مجموعه مراجعه کنید)

$|x| < c \Leftrightarrow -c < x < c \,\,\, (\forall c \in \Bbb{R}^{+})$

$|x| \le c \Leftrightarrow -c \le x \le c \,\,\, (\forall c \in \Bbb{R}^{+})$

$|x| > c \Leftrightarrow (x > c) \cup (x < -c) \,\,\, (\forall c \in \Bbb{R}^{+})$

$|x| \ge c \Leftrightarrow (x \ge c) \cup (x \ge -c) \,\,\, (\forall c \in \Bbb{R}^{+})$

توجه: به نکات زیر برای محاسبه برخی عبارات قدرمطلقی توجه کنید:

*اگر دو عدد $a$ و $b$ هم علامت باشند داریم:

$|a+b|=|a|+|b|$

* اگر دو عدد $a$ و $b$ هم علامت و مثبت باشند داریم:

$|a+b|=a+b$

* اگر دو عدد $a$ و $b$ هم علامت و منفی باشند داریم:

$|a+b|=-(a+b)$

**اگر دو عدد $a$ و $b$ مختلف العلامت باشند داریم:

$|a+b|=||a|-|b||$

* اگر دو عدد $a$ و $b$ هم علامت باشند داریم: $ab >0$

* اگر دو عدد $a$ و $b$ مختلف العلامت باشند داریم: $ab <0$

مثال: حاصل عبارات زیر را بدست آورید:

$|(-5)+(-10)|\,\,\, and \,\,\, |(+7)+(-12)|$

جواب: با توجه به نکات بالا در مورد قدرمطلق جمع اعداد هم علامت و مختلف العلامت داریم:

$|(+7)+(-12)|=||+7|-|-12||=$

$=|7-12|=|-5|=+5$

$|(-5)+(-10)|=|-5|+|-10|==$

$=5+10=15$

چطور جمع و تفریق عبارات قدرمطلقی را محاسبه کنیم؟

برای جمع و تفریق عبارات قدرمطلقی کافی است که به نکات قبلی برای بدست آوردن قدرمطلق توجه کنیم و سپس عمل جمع و تفریق را برای حاصل قدرمطلق ها محاسبه می کنیم.

مثال: حاصل جمع و تفریق عبارات قدرمطلقی را بدست آورید.

$|2-\sqrt{3}|-|\sqrt{7}-2\sqrt{2}|$

$=2-\sqrt{3}-(2\sqrt{2}-\sqrt{7})$

$=2-\sqrt{3}-2\sqrt{2}+\sqrt{7}$

$|\sqrt{5}-7|+|-3-\sqrt{5}|$

$=7-\sqrt{5}+3+\sqrt{5}=10$

$| 17-2\sqrt{5} |+|4-5\sqrt{5} |$

$=17-2\sqrt{5}-4+5\sqrt{5}$

$=3\sqrt{5}+13$

چطور یک تابع قدرمطلقی را رسم کنیم؟

رسم توابع قدرمطلقی یک موضوع مهم است که شامل دو حالت می شود. حالت اول اینکه شکل تابع را بدهند و بخواهند شکل قدر مطلق آن را رسم کنیم. حالت دوم ضابطه تابع را بدهند و بخواهند قدر مطلق آن را رسم کنیم. در حالت دوم عموما تابع از نوع درجه یک و خطی است.

برای رسم تابع قدرمطلقی در حالت اول باید به این نکته توجه کرد که نمودار $y=-f(x)$ قرینه نمودار $y=f(x)$ نسبت به محور $x$ هاست. برای رسم نمودار $y=| f(x) |$ کافی است نمودار $y=f(x)$ را رسم کنیم و در جاهایی که نمودار $f(x)$ زیر محور $x$ هاست تصویر آینه وار نمودار $f(x)$ را نسبت به محور $x$ ها رسم کنیم. در واقع به ازای $f(x)$ های منفی، منحنی را نسبت به محور $x$ ها قرینه می کنیم.

در حالت دوم که ضابطه را می دهند در بسیاری از سوالات این ضابطه از درجه اول است پس برای رسم نمودار قدرمطلقی آن دو راه داریم راه اول اینکه از تبدیل نمودار توابع کمک بگیریم و با توجه به نکات انتقال توابع ، تابع قدرمطلق را انتقال دهیم تا تابع مورد نظر را رسم کنیم. راه دوم اینکه تابع قدرمطلقی در سوال را به صورت تابع دو ضابطه ای بنویسیم و سپس آن تابع دو ضابطه ای را رسم کنیم.

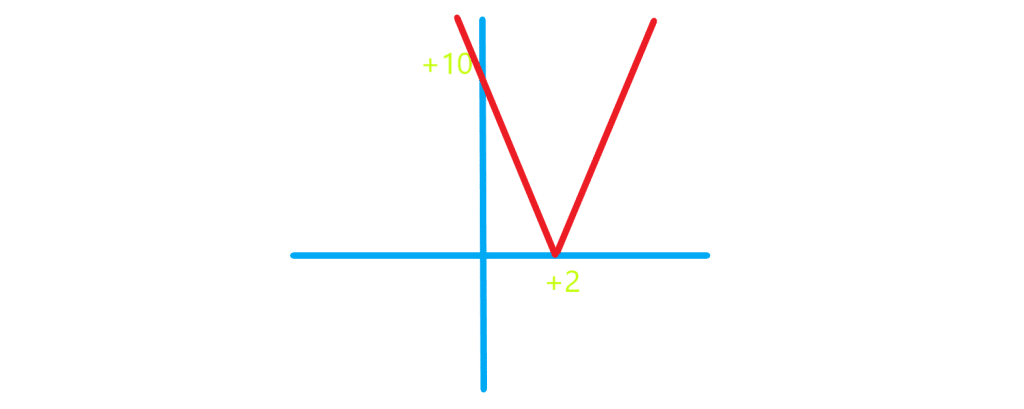
مثال: تابع $| -5x+10 |$ را رسم کنید (با دو روش)

جواب: راه اول: اولین مرحله رسم نمودار تابع $| x|$ است. در مرحله دوم با توجه به نکات گفته شده در مقاله ی رسم نمودار توابع ابتدا تابع $| x |$ را $10$ واحد به سمت چپ می بریم و بعد اعداد محور $x$ ها را بر عدد $-5$ تقسیم می کنیم. به شکل زیر توجه کنید:

راه دوم: ابتدا تابع $|-5x+10 |$ را بصورت تابع دو ضابطه ای زیر می نویسیم.

$|-5x+10|=\begin{cases} -5x+10 & -5x+10 \ge 0 \\ -(-5x+10) & -5x+10 < 0\end{cases}$

$=\begin{cases} -5x+10 & x \le +2 \\ -(-5x+10) & x \ge +2 \end{cases}$

سپس هر ضابطه را در بازه مربوط به خودش رسم می کنیم. برای رسم این تابع، ابتدا باید برای رسم هر ضابطه که یک تابع خطی است دو نقطه داشته باشیم و هر دو نقطه را به هم وصل کنیم تا تابع خطی رسم شود.

برای ضابطه اول که باید در بازه $x \le +2$ رسم شود می توان $x=+2$ و $x=+1$ را بعنوان طول های دو نقطه در نظر گرفت. برای عرض نظیر هر دو نقطه باید این طول ها را در ضابطه $y=-5x+10$ قرار دهیم. بدست می آید:

$y=-5(+1)+10=5$

$and \,\,\, y=-5(+2)+10=0$

برای ضابطه دوم که باید در بازه $x \ge +2$ رسم شود می توان $x=+2$ و $x=+3$ را بعنوان طول های دو نقطه در نظر گرفت. برای عرض نظیر هر دو نقطه باید این طول ها را در ضابطه $y=-(-5x+10)=5x-10$ قرار دهیم. بدست می آید:

$y=5(+3)-10=5$

$and \,\,\, y=5(+2)-10=0$

باتوجه به نقاط بدست آمده دو نیم خط که هر کدام مربوط به یک ضابطه هستند را رسم می کنیم. به شکل زیر توجه کنید:

می بینیم شکل حاصل از هر دو راه حل یکسان هستند.

چطور یک معادله قدرمطلقی را حل کنیم؟

جواب های معادله $| f(x) |=| g(x) |$ همان جواب های دو معادله $f(x)=g(x)$ و $f(x)=-g(x)$ هستند به معادلاتی نظیر این معادلات که شامل عبارت قدرمطلق هستند معادلات قدرمطلقی می گویند.

مثال: جواب معادلات زیر را بدست آورید:

* $| 3x+7|=|-2x-9|$

** $|2x^{2}-3x-12|=| x^{2}+5x+7|$

جواب : برای حل سوالات باید بر حل معادله خطی و حل معادله درجه دو تسلط داشته باشیم.

*سوال اول یک معادله قدرمطلقی شامل دو عبارت خطی است. برای حل این معادله با توجه به آنچه پیشتر گفته شده باید دو معادله خطی را حل کنیم:

$3x+7=-(-2x-9)$

$and \,\,\, 3x+7=-2x-9$

$3x+7=-2x-9\,\,\rightarrow \,\, 3x+2x=-9-7$

$\rightarrow \,\, 5x=-16\,\, \rightarrow \,\, x=\frac{-16}{5}$

$3x+7=-(-2x-9)=2x+9\,\,\,\rightarrow$

$3x-2x=+9-7\,\,\,\rightarrow \,\,\,x=2$

بنابراین این معادله قدرمطلقی دارای دو پاسخ هست: $x=\frac{-16}{5} \,\, ,\,\, x=2$

**سوال دوم یک معادله قدرمطلقی شامل دو عبارت درجه دو است برای حل این معادله قدرمطلقی باید دو معادله درجه دو را حل کنیم:

$2x^{2}-3x-12=-x^{2}-5x-7$

$and \,\,\,2x^{2}-3x-12=x^{2}+5x+7$

$2x^{2}-3x-12=x^{2}+5x+7\,\,\rightarrow$

$2x^{2}-x^{2}-3x-5x-12-7=0$

$\rightarrow \,\, x^{2}-8x-19=0$

برای حل این معادله درجه دو باید از یکی از روش های حل معادله درجه دو استفاده کرد که در اینجا از روش $\Delta$ استفاده می کنیم.

$\Delta=64+4\times 19=140\,\,\rightarrow$

$x=\frac{8+\sqrt{140}}{2}\,,\,x=\frac{8-\sqrt{140}}{2}$

برای حل معادله دوم هم عملیات مشابه انجام می دهیم:

$2x^{2}-3x-12=-x^{2}-5x-7\,\,\rightarrow$

$2x^{2}+x^{2}-3x+5x-12+7=0$

$3x^{2}+2x-5=0\,\,\rightarrow$

$\Delta=4+60=64\,\,\rightarrow$

$x=\frac{-2+\sqrt{64}}{6}=+1$

$x=\frac{-2-\sqrt{64}}{6}=\frac{-10}{6}$

بنابراین این معادله قدرمطلقی دارای چهار پاسخ است:

$x=\frac{8+\sqrt{140}}{2}\,,\, x=\frac{8-\sqrt{140}}{2}$

$x=\frac{-10}{6}\,,\,x=+1$

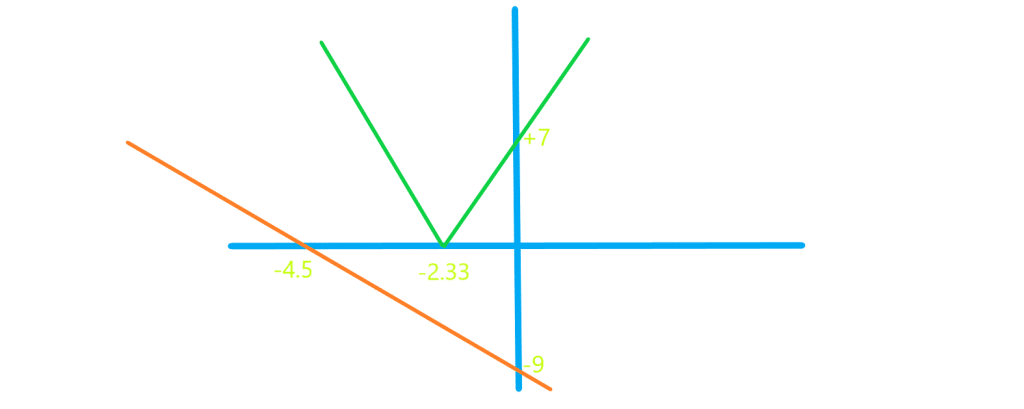
مثال: معادله قدرمطلقی $|3x+7|=|-2x-9|$ با $|3x+7|=-2x-9$ متفاوت است دلیل آن این است که حاصل قدرمطلق حتما باید مثبت باشد در عبارت اول حاصل قدرمطلق $|3x+7|$ یک عبارت قدرمطلقی دیگر است که حتما مثبت است. اما در عبارت دوم حتما باید بررسی شود که حاصل قدرمطلق $|3x+7|$ مثبت هست یا نه. برای اینکه این سبک عبارات قدرمطلقی را محاسبه کنیم سه روش وجود دارد: استفاده از تعریف قدرمطلق – استفاده از رسم تابع – به توان دوم رساندن طرفین.

تعریف قدرمطلق:

$| 3x+7|=\begin{cases} 3x+7 & x \ge \frac{-7}{3}\\-3x-7 & x < \frac{-7}{3} \end{cases} \rightarrow$

$\begin{cases}3x+7=-2x-9 & x \ge \frac{-7}{3} \\ -3x-7=-2x-9 & x < \frac{-7}{3} \end{cases}$

$\rightarrow \,\,\, \begin{cases} 5x=-16 & x \ge \frac{-7}{3} \\ x=2 & x < \frac{-7}{3} \end{cases} \rightarrow$

$\begin{cases} x=\frac{-16}{5} < \frac{-7}{3} \\ x=2 > \frac{-7}{3} \end{cases}$

می بینیم هر دو جواب در شرط محدوده $x$ صدق نمی کنند پس برخلاف سوال قبل این معادله قدرمطلقی جواب ندارد.

راه دوم : روش ترسیم هندسی : می توانیم هر دو تابع $| 3x+7|$ و $-2x-9$ را مطابق شکل زیر رسم کنیم سپس بررسی کنیم که آیا این دو شکل با هم محل برخوردی دارند یا نه . اگر تقاطعی داشتند محل تقاطع ها همان جواب های معادله اند و اگر تقاطعی نداشتند پس معادله جواب ندارد. همانطور که در شکل زیر می بینید این دو شکل هیچ محل برخوردی ندارند پس معادله جواب ندارد.

راه سوم به توان رساندن طرفین: برای این کار توان دوم هر دو طرف تساوی را حساب می کنیم و برابر همدیگر قرار می دهیم $(-2x-9)^{2}=( |3x+7|)^{2}$ حالا این دو را به توان می رسانیم:

$4x^{2}+36x+81=9x^{2}+42x+49$

در مرحله بعد این تساوی را ساده و سپس حل می کنیم:

$4x^{2}+36x+81=9x^{2}+42x+49\,\,\,\rightarrow$

$5x^{2}+6x-32=0$

$\rightarrow \Delta=6^{2}-(4)(5)(-32)=676 \rightarrow \,\,\,\sqrt{676}=26$

$\rightarrow \,\,\,x=\frac{-6+26}{10}=2 \,\,,\,\,x=\frac{-6-26}{10}=-3.2$

در مرحله آخر باید بررسی کنیم آیا جواب ها حاصل قدرمطلق را منفی نمی کند؟ اگر حاصل عبارت جلوی قدرمطلق به ازای این اعداد منفی نشد که قابل قبولند اگر منفی شد غیرقابل قبولند و معادله جواب ندارد.

$-2x-9=-2\times 2-9=-13 < 0$

$-2x-9=-2\times (-3.2)-9=-2.6 < 0$

پس معادله جواب ندارد.

چطور نامعادله قدرمطلقی را حل کنیم؟

برای حل نامعادله قدرمطلقی می توان از هر سه روش رسم هندسی توان دوم و تعریف قدرمطلق استفاده کرد.

فرض کنیم $a$ یک عدد حقیقی مثبت و $u$ یک عبارت جبری باشد . در این صورت :

اگر $|u| \le a$ آنگاه $-a \le u \le a$

اگر $| u| \ge a$ آن گاه $u \le -a$ یا $u \ge a$ .

روش هندسی: در روش هندسی هر دو طرف نامساویِ $| f(x) | < | g(x) |$ را رسم می کنیم. بازه هایی که نمودار $|f(x)|$ زیر نمودار $|g(x)|$ است همان جواب نامعادله است.

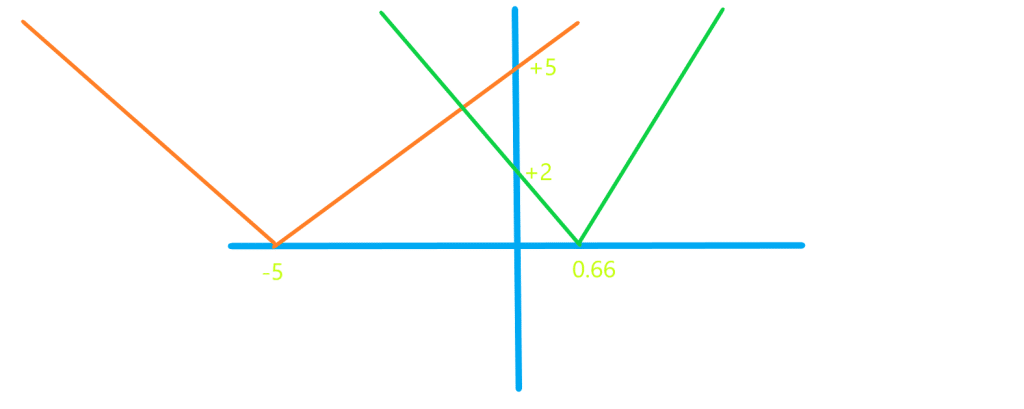
مثال : نامعادله قدرمطلقی $| 2-3x | < |x+5|$ را حل کنید.

جواب: با توجه به آنچه که در قسمت رسم توابع قدرمطلقی گفته شده هر دو تابع قدرمطلقی را مطابق شکل زیر در یک صفحه مختصات رسم می کنیم. مهمانطور که می بینیم در بازه $[\frac{-3}{4},\frac{7}{2}]$ نمودار $| 2-3x |$ پایین تر از نمودار $| x+5 |$ قرار دارد. پس جواب بازه $[\frac{-3}{4},\frac{7}{2}]$ است.

روش توان دوم: در این روش برای بدست آوردن جواب نامعادله قدرمطلقی $|f(x) | < |g(x) |$ ابتدا باید دو طرف نامساوی را به توان دوم برسانیم $f^{2}(x) < g^{2}(x)$ حالا این نامساوی جدید را حل می کنیم بعد جواب های بدست آمده را در نامساوی قدرمطلقی $|f(x) | < |g(x) |$ بررسی می کنیم که ببینیم آیا به ازای آن جواب ها نامساوی برقرار است یا نه.

مثال : نامعادله قدرمطلقی $|2-3x | < |x+5 |$ را حل کنید.

جواب: برای حل نامعادله قدرمطلقی به روش توان دوم ابتدا دو طرف نامساوی را به توان دو می رسانیم.

$| 2-3x |^{2} < |x+5| ^{2}$

$\rightarrow \,\,\, 4-12x+9x^{2} < x^{2}+10x+25$

$\rightarrow \,\,\, 8x^{2}-2x-21 < 0$

$\rightarrow \Delta =22^{2}-4\times 8 \times (-21) =1156$

$\rightarrow \,\,\, \sqrt{\Delta} =34$

$\rightarrow x=\frac{22-34}{16}=-0.75$

$x=\frac{22+34}{16}=3.5$

$\rightarrow \,\, -0.75 < x < 3.5$

روش سوم تعریف قدرمطلق: این روش بخاطر طولانی بودن توصیه نمی شود چرا که باید هر دو طرف نامساوی را بصورت دو ضابطه ای نوشت و بعد در هر بازه از $x$ به صورت جداگانه نامساوی را حل کرد و بعد شروط را بررسی کرده و در نهایت جواب را بیابیم در واقع برای حل سوال نامعادله قدرمطلقی در صورت درجه یک بودن هر دو عبارت باید سه نامساوی مجزا حل کنیم

جمع بندی

این مقاله به تعریف قدرمطلق و خواص قدرمطلق پرداخته است. همچنین روش هایی برای محاسبه عبارت قدرمطلقی شامل رادیکال، جمع و تفریق عبارات قدرمطلقی و رسم توابع قدرمطلقی داده است. معادلات و نامعادلات قدرمطلقی نیز با سه روش متفاوت قابل حل هستند که در این مقاله هر سه روش به طور کامل بیان شده است. اگر تمایل دارید که به صورت جامع و بهمراه نمونه سوالات کنکور و نهایی در سالهای مختلف این مطالب را بیاموزید دوره جبر معادله تابع فرامث را تهیه کنید. لطفا نظر خود و یا سوالات تان در مورد مقاله قدرمطلق را در قسمت کامنت ها بنویسید.

همه چیز درباب قدرمطلق، توابع قدرمطلقی و رسم آنها، معادله و نامعادله قدرمطلقی

تعریف قدرمطلق، چطور حاصل یک عبارت قدرمطلقی را بدست آوریم؟

ویژگی ها و خواص قدرمطلق چیست؟

چطور جمع و تفریق عبارات قدرمطلقی را محاسبه کنیم؟

چطور یک تابع قدرمطلقی را رسم کنیم؟

چطور یک معادله قدرمطلقی را حل کنیم؟

چطور نامعادله قدرمطلقی را حل کنیم؟

دیدگاهتان را بنویسید لغو پاسخ

آخرین مطالب وبلاگ

دنباله های عددی

تابع خطی و معادله خط

تابع و دامنه و برد آن

تعیین علامت

عبارت و معادله گویا

معادله درجه دوم

معادله

عبارت جبری

قدرمطلق

دوره ها

دسترسی سریع

دسترسی سریع

مقالات مادر