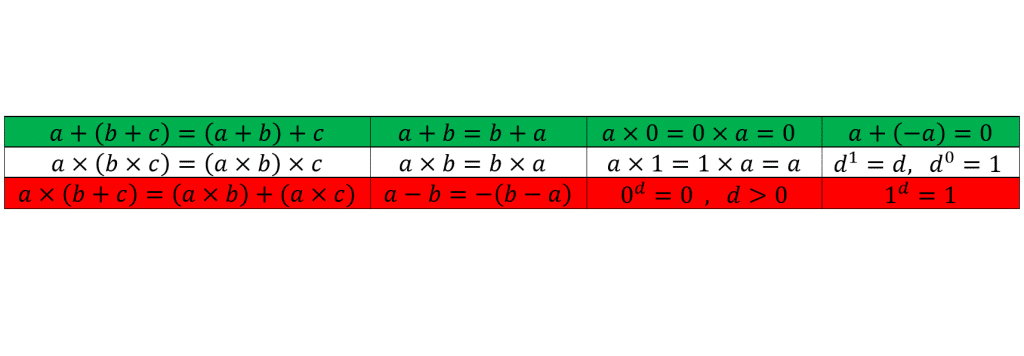جامع ترین آموزش در معرفی عبارات جبری، اتحادها وقوانین ریاضی به زبان جبر

عبارت جبری و اتحادها علمی است که به همت خوارزمی پایه گذاری شده و اساس بسیاری از علوم مانند علوم کامپیوتر و هوش مصنوعی می باشد. در این مقاله به بیان تعریف عبارت جبری و جملات متشابه جبری و همجنین نحوه جمع و تفریق و ضرب و تقسیم آنها می پردازیم. تبدیل عبارت کلامی به جبری و برعکس هم از مواردی است که در این مقاله به آموزش آن پرداختیم. همچنین اگر می خواهید همه ی اتحادها را یکجا آموزش ببینید این مقاله را از دست ندهید.

عبارت جبری چیست؟

از مقاله ی محیط و مساحت می دانیم که محیط مربع چهار برابر ضلع مربع است. اگر محیط مربع را با $P$ نشان دهیم و ضلع مربع را با $a$ می توان نوشت: $P=4a$ . حالا اگر به جای $a$ اعداد مختلفی قرار دهیم مقادیر متفاوتی برای $P$ بدست می آید. یعنی هر عددی برای ضلع به ما بدهند می توانیم با کمک این فرمول محیط مربع را برای هر کدام جداگانه بدست آوریم. $4a$ یک عبارت جبری است و $a$ متغیر آن است. در جبر، متغیرها،نمادهایی برای بیان اعداد نامعلوم یا مقادیر نامشخص هستند. یک عبارت جبری شامل یک یا چند عدد، متغیر و عمل هایی مثل جمع و تفریق و ضرب و تقسیم است.

برای نوشتن قوانین ریاضی مثل خاصیت جابجایی جمع $(a+b=b+a)$ یا عبارات کلی برای بررسی هزینه ها یا پیشرفت کار یا … می توان از عبارت جبری استفاده کرد.

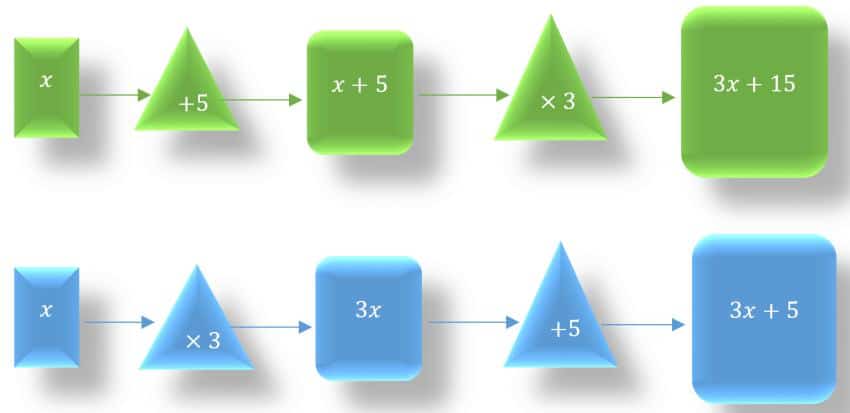
خروجی هر ماشین زیر یک عبارت جبری است چرا که به ازای اعداد مختلفی که می توان به جای متغیرها گذاشت مقادیر متفاوتی برای عبارت جبری بدست می آید.

مشاهده می کنید عوض کردن ترتیب اعمالِ ریاضی عبارت جبری متفاوتی را ایجاد می کند و $3x+5 \neq 3x+15$ می باشد.

یک عبارت جبری شامل یک یا چند عدد حقیقی، متغیر و اعمال ریاضی شامل جمع، تفریق، ضرب و تقسیم است. در زیر نمونه هایی از عبارت جبری آورده شده است:

$-2s \,,\,\, \sqrt{5}c\,,\,\, 3x-8 \, ,\,\, \frac{p}{q}-2w\,,\,\, 3m\times (-9)n$

نکته: در یک عبارت جبری اغلب از علامت (.) یا پرانتز برای حاصل ضرب استفاده می شود. و از نماد پرهیز می شود زیرا ممکن است علامت ضربدر با حرف $x$ بعنوان متغیر اشتباه شود.

$xy=x.y=x(y)=(x)y=(x)(y)$

چطور قوانین ریاضی را با کمک عبارت جبری نشان دهیم؟

برای اینکه نشان دهیم یک سری قوانین ریاضی به ازای همه ی اعداد حقیقی برقرار است می توان از عبارت جبری کمک گرفت چون به جای متغیرها می توان هر عدد دلخواهی قرار داد.

در جمع خاصیت جابجایی وجود دارد به این صورت که ترتیب اعداد موقع جمع کردن اهمیت ندارد.

$a+b=b+a$

در ضرب خاصیت جابجایی وجود دارد به این صورت که ترتیب اعداد موقع ضرب کردن اهمیت ندارد.

$a \times b=b \times a$

هر عدد ضرب در عدد یک برابر با خودش است.

$a \times 1=1 \times a=a$

حاصلضرب هر عدد در عدد صفر برابر با صفر است.

$a \times 0=0 \times a=0$

هر عبارت با عدد برابر با قرینه ی قرینه اش است.

$a-b=-(b-a)$

جمع هر عدد با قرینه اش برابر با صفر است.

$a+(-a)=0$

در جمع خاصیت پخشی وجود دارد به این صورت که اگر سه عدد را می خواهید جمع کنید فرقی ندارد که کدام دو عدد را اول جمع می کنید.

$a+(b+c)=(a+b)+c$

در ضرب خاصیت پخشی وجود دارد به این صورت که اگر سه عدد را می خواهید در هم ضرب کنید فرقی ندارد که کدام دو عدد را اول ضرب می کنید.

$a \times (b \times c ) =( a \times b ) + (a \times c )$

اگر عددی را در یک پرانتز ضرب کنیم در واقع باید آن عدد را در تک تک اعداد داخل پرانتز ضرب کنیم.

$a \times ( b+c) =( a \times b ) +( a \times c)$

هر عدد به توان یک برابر با خود عدد است.

$d^{1}=d$

هر عدد به توان صفر برابر با یک است.

$d^{0}=1$

یک به توان هر عدد برابر با یک است

$1^{d}=1$

صفر به توان هر عدد مثبت برابر با صفر می شود.

$0^{d}=0 \,\,\, , \,\,\, d > 0$

چه موقع دو عبارت جبری متشابه اند؟

به عبارت جبری ای که فقط شامل حاصل ضرب متغیرها (حروف انگلیسی) و اعداد باشد یک جمله می گویند. برای اینکه دو جمله متشابه باشند باید دو شرط برای آنها برقرار باشد: 1-متغیرهای یکسان داشته باشند 2-توان متغیرهایشان برابر باشد.

برای مثال جملات متشابه را در یک پرانتز گذاشتیم.

$(2a\,\, , \,\, -3a \,\,,\,\,\sqrt{12}a \,\,, \,\,\frac{3}{7}a\,\,,\,\,1.008a)$

$(2ab\,\,,\,\,-9ba\,\,,\,\,32ab)\,\,\,\,,\,\,\,\,(-2d^{3}c\,\,,\,\,5cd^{3})$

و جملات $(2a\,\,,\,\,-3x\,\,,\,\,\sqrt{12}z\,\,,\,\,\frac{3}{7}\,\,,\,\,1.008b)$ با هم متشابه نیستند چون متغیرهای یکسان ندارند همچنین جملات $(2a^{2}b\,\,,\,\,-9ba\,\,,\,\,32ab^{2})$ با هم متشابه نیستند. چون با اینکه متغیرها یکسانند اما توان های یکسان ندارند.

عبارت دو جمله ای: به حاصل جمع یا تفریق دو جمله ی غیرمتشابه عبارت دو جمله ای می گویند. مثلا $3x+2a$ یا $2a-1$ یا $7a^{2}-5$ .

عبارت چندجمله ای: به حاصل جمع یا تفریق بیشتر از دو جمله ی غیرمتشابه چند جمله ای می گویند. مثلا $3x+2a+1$ یا $8a^{3}+7a^{2}-5a+2$ .

چه موقع می توان دو عبارت جبری را جمع یا تفریق کرد؟ چگونه؟

جملات جبری را فقط در صورتی می توان جمع یا تفریق کرد که متشابه باشند.

مثال : عبارت جبری زیر را تا حد امکان ساده کنید؟

$2a-3a-\sqrt{12}a+\frac{3}{7}a+1.008a$

$=(2-3-\sqrt{12}+\frac{3}{7}+1.008)a$

$=(0.008-\sqrt{12}+\frac{3}{7})a$

برای ساده کردن عبارات جبری فقط کافی است قسمت پارامتریِ مشترک (متغیرها به همراه توان شان ) را فاکتور بگیریم و بعد با توجه به قوانین جمع و تفریق اعداد صحیح به جمع و تفریق ضرایب آنها بپردازیم.

مثال: عبارات جبری زیر را ساده کنید.

$(5n+7)-(-6n+5)-(2n-8)$

$=5n+7+6n-5-2n+8$

$=(5+6-2)n+(7-5+8)=9n+10$

چطور می توان دو عبارت جبری را ضرب یا تقسیم کرد؟

در ضرب عبارت جبری ضرایب عددی را در هم ضرب می کنیم و برای متغیر های مشترک توان ها را با هم جمع می کنیم و متغیر های غیر مشترک را می نویسیم. (برای مطالعه قوانین ضرب و تقسیم اعداد توان دار می توانید به مطالعه مقاله توان بپردازید.)

مثال: حاصل ضرب زیر را بدست آورید.

$-2a^{3}b^{4}\times 53a^{6}b^{12}$

$=(-2\times 53)(a^{3}\times a^{6})(b^{4} \times b^{12})=-106a^{9}b^{16}$

در تقسیم عبارات جبری ضرایب عددی را تقسیم می کنیم و برای متغیرها از قوانین تقسیم اعداد توان دار کمک می گیریم.

مثال: حاصل تقسیم زیر را بدست آورید.

$-12a^{3}b^{4} \div 6ab^{7}=\frac{-12a^{3}b^{4}}{6ab^{7}}$

$=\frac{-12}{6}\times \frac{a^{3}}{a}\times \frac{b^{4}}{b^{7}}=$

$-2\times \frac{a^{2}}{1} \times \frac{1}{b^{3}}=\frac{-2a^{2}}{b^{3}}$

چطور می توان عبارت کلامی را تبدیل به یک عبارت جبری کرد؟

برای تبدیل عبارت کلامی به جبری باید کلماتی که نشان دهنده ی یک عبارت کلی هستند مثل “یک عدد” ” عددی ” را به عنوان متغیر در نظر گرفت و بعد بررسی کنید که عبارت کلامی داده شده می خواهد با آن عدد چکار کند ( آن را چند برابر کند یا تقسیم کند زیاد کند یا کم کند قرینه کند یا …). برای اینکه بهتر متوجه شوید به مثال های زیر توجه کنید.

مثال: هفت تا بیشتر از عددی

جواب : $x+7$

مثال: سه تا کمتر از چهار برابر عددی

جواب: $4x-3$

مثال: یک چهارم مساحت

جواب: $\frac{1}{4}s$

چطور مقدار عددی یک عبارت جبری را بدست آوریم؟

اگر به جای متغیر یا متغیرها در عبارت جبری عدد معینی قرار دهیم مقدار عددی آن عبارت جبری بدست می آید.

برای اینکه بهتر متوجه این فرآیند شوید به مثال زیر توجه کنید:

مثال: مقدار عددی عبارت جبری $5(2x-3y)-(2y-3x)$ را به ازای $x=2\,\,\,y=1$ بدست آورید.

جواب: برای اینکه بتوانیم به جواب سوال برسیم اول باید توجه کنیم که $2x$ یعنی دو ضربدر $x$ و برای محاسبه کل عبارت اول باید مقدار عددی ِ عبارت داخل پرانتز را بدست آوریم. (برای اینکه ترتیب عملیات را درست انجام دهید سری به مقاله اعداد صحیح بزنید) بنابراین داریم:

جواب:

$5(2x-3y)-(2y-3x)$

$=5(2\times2-3\times1)-(2\times1-3\times 2)$

$=5(4-3)-(2-6)=5(1)-(-4)$

$=5+4=9$

برای بدست آوردن مقدار عددی عبارت جبری یک راه دیگر هم وجود دارد. می توانید ابتدا عبارت جبری را ساده کنید سپس مقادیر عددی را به جای متغیرها قرار دهید. این روش مخصوصا برای زمانی مناسب است که مقادیر عددی از اعداد بزرگ اند و محاسبه با آنها سخت است.

برای مثال سوال قبلی را به این روش حل می کنیم:

$5(2x-3y)-(2y-3x)$

$=10x-15y-2y+3x$

$=13x-17y=13\times2-17\times1$

$=26-17=9$

توجه کنید در این گونه سوالات که عددی با علامت منفی ( علامت هر عدد در سمت چپ آن عدد قرار می گیرد) در یک پرانتز ضرب می شود در واقع در تک تک اعداد داخل پرانتز ضرب می شود. مثلا در $-(2y-3x)$ عدد $-1$ را یکبار در $2y$ یکبار در $-3x$ ضرب می کنیم و حاصل این ضرب ها را با هم جمع می کنیم تا به جواب برسیم.

نکته: عدد دو رقمی $ab$ را با نماد $\overline{ab}$ نمایش می دهیم بنابراین $\overline{ab}=10a+b$

تجزیه عبارت جبری: چطور یک عبارت جبری را می توان تجزیه کرد؟

در عبارت های جبری هم مانند اعداد خاصیت توزیع پذیری و تجزیه وجود دارد. خاصیت توزیع پذیری به صورت زیر نمایش داده می شود:

$a\times (b+c)=(a \times b)+(a \times c)$

خاصیت تجزیه کردن برعکس توزیع پذیری است و به صورت زیر نمایش داده می شود:

$(a\times b)+(a\times c)=a \times (b+c)$

یا به صورت معمول تر $ab+ac=a(b+c)$

در واقع برای تجزیه یک عبارت جبری باید دید بین جملاتی که با هم جمع یا تفریق شدند چه عوامل مشترکی وجود دارد. بعد آن عوامل مشترک به سان $a$ در نکته تجزیه کردن شده و بیرون از پرانتز به صورت حاصل ضرب قرار می گیرند.

برای مثال برای تجزیه عبارت چندجمله ای $6x^{4}y^{3}+3x^{7}y^{7}z-15xy^{3}z^{2}$ باید به این مسئله توجه کنیم ضرایب عددی یعنی 6 و 3 و 15 بزرگترین شمارنده مشترکشان چه عددی است. در گام بعدی باید ببینیم چه متغیرهایی در هر سه جمله تکرار شده اند می بینیم $x$ و $y$ در هر سه جمله وجود دارد اما $z$ در هر سه جمله وجود ندارد. با این تفاسیر از بزرگترین شمارنده مشترک 6 و 3 و 15 یعنی عدد 3 و از حروف مشترک $x$ و $y$ با توان کمتر فاکتور می گیریم. داریم:

$6x^{4}y^{3}+3x^{7}y^{7}z-15xy^{3}z^{2}$

$=3xy^{3}(2x^{3}+x^{6}y^{4}z-5yz^{2})$

اتحادهای جبری

اگر دو عبارت جبری به گونه ای باشند که به ازای هر مقدار برای متغیر هایشان حاصل یکسانی داشته باشند، برابری جبری حاصل از آنها را اتحاد جبری می نامیم.

اتحاد مربع دو جمله ای

برای هر دو عدد حقیقی $a$ و $b$ داریم:

$(a+b)^{2}=a^{2}+2ab+b^{2}$

$(a-b)^{2}=a^{2}-2ab+b^{2}$

مثال : حاصل $(5-2\sqrt{2})^{2}$ و $(\sqrt{2}+3\sqrt{3})^{2}$ را بدست آورید.

جواب: با توجه به اتحاد مربع دو جمله ای داریم:

$(5-2\sqrt{2})^{2}$

$=5^{2}-2\times 5 \times 2\sqrt{2}+(2\sqrt{2})^{2}$

$=25-20\sqrt{2}+8$

$=33-20\sqrt{2}$

$(\sqrt{2}+3\sqrt{3})^{2}$

$=\sqrt{2}^{2}-2\times \sqrt{2}\times 3\sqrt{3}+(3\sqrt{3})^{2}$

$=2-6\sqrt{6}+27$

$=29-6\sqrt{6}$

اتحاد مزدوج

$(a+b)(a-b)=a^{2}-b^{2}$

عبارت $a^{2}-16$ را به صورت حاصل ضرب دو عبارت بنویسید.

جواب: چون هم $a^{2}$ و هم $16=4^{2}$ مربع کامل هستند با توجه به اتجاد مزدوج داریم :

$a^{2}-16=(a+4)(a-4)$

اتحاد مربع سه جمله ای

$(a+b+c)^{2}=$

$a^{2}+b^{2}+c^{2}+2ab+2ac+2bc$

مثال: مربع $\sqrt{2}+3+c$ را پیدا کنید.

جواب چون سه جمله با هم جمع شده اند و مربع شان خواسته شد بنابراین باید از اتحاد مربع سه جمله ای استفاده کنیم. داریم:

$(\sqrt{2}+3+c)^{2}$

$=\sqrt{2}^2+3^{2}+c^{2}+6\sqrt{2}+2\sqrt{2}c+6c$

$=4+9+6\sqrt{2}+c^{2}+(2\sqrt{2}+6)c$

$=c^{2}+(2\sqrt{2}+6)c+(13+6\sqrt{2})$

اتحاد جمله مشترک

$(x+a)(x+b)=x^{2}+(a+b)x+ab$

مثال: حاصل $(3x+5)(3x-2)$ را بدست آورید.

جواب: با توجه به اینکه یک جمله یعنی $3x$ در هر دو پرانتز وجود دارد باید از اتحاد جمله مشترک استفاده کنیم. داریم:

$(3x+5)(3x-2)$

$=9x^{2}+(5-2)x-10$

$=9x^{2}+3x-10$

اتحاد مکعب دو جمله ای

$(a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3}$

$(a-b)^{3}=a^{3}-3a^{2}b+3ab^{2}-b^{3}$

مثال: مکعب عبارت $\sqrt{2}-b$ را بدست آورید.

جواب: با توجه به اینکه دو جمله داریم و سوال مکعب تفریق این دو جمله را می خواهد از اتحاد مکعب دو جمله ای استفاده می کنیم. داریم:

$(\sqrt{2}-b)^{3}=$

$\sqrt{2}^{3}-3\sqrt{2}^{2}b+3\sqrt{2}b^{2}-b^{3}$

اتحاد چاق و لاغر

$a^{3}+b^{3}=(a+b)(a^{2}-ab+b^{2})$

$a^{3}-b^{3}=(a-b)(a^{2}+ab+b^{2})$

مثال: عبارت $\sqrt{7}^{3}+\sqrt{8}^{3}$ را به صورت حاصل ضرب دو عدد بنویسید.

جواب از آنجا که دو عدد داریم که هر دو توان سه دارند پس باید از اتحاد چاق و لاغر استفاده کنیم. (اگر محاسبات مربوط به اعداد رادیکالی را بلد نیستید به مقاله اعداد گنگ و مقاله جذر و ریشه مراجعه کنید) داریم:

$\sqrt{7}^{3}+\sqrt{8}^{3}=$

$(\sqrt{7}+\sqrt{8})(\sqrt{7}^{2}-\sqrt{7}\times \sqrt{8} +\sqrt{8}^{2})$

$=(\sqrt{7}+\sqrt{8})(15-\sqrt{56})$

نکته: در حالت کلی می توان اتحاد چاق و لاغر را می توان از درجه 3 به درجه $n \in \Bbb{N}$ بسط داد. داریم:

$x^{n}-a^{n}=(x-a)(x^{n-1}+ax^{n-2}+…+a^{n-2}x+a^{n-1})$

در حالتی که $n$ یک عدد فرد باشد داریم:

$x^{n}+a^{n}=(x+a)(x^{n-1}-ax^{n-2}+…-a^{n-2}x+a^{n-1})$

اتحاد اویلر

دو نمایش برای اتحاد اویلر وجود دارد :

$(a+b+c)(a^{2}+b^{2}+c^{2}-ab-ac-bc)$

$=a^{3}+b^{3}+c^{3}-3abc$

یا

$(a+b+c)((a-b)^{2}+(b-c)^{2}+(a-c)^{2})$

$=2a^{3}+2b^{3}+2c^{3}-6abc$

از این دو نمایش می توان نتیجه گرفت :

اگر $a+b+c=0$ آنگاه $a^{3}+b^{3}+c^{3}=3abc$

اگر $a=b=c$ آنگاه $a^{3}+b^{3}+c^{3}=3abc$

همه ی اتحادها را می توانید در جدول زیر ببینیذ:

همه ی قوانین ریاضی به زبان جبری را در جدول زیر می توانید ببینید:

جمع بندی

در این مقاله عبارت جبری را تعریف کردیم و گفتیم چه عبارات جبری ای متشابه اند و چطور عبارات جبری را جمع و تفریق و ضرب و تقسیم کنیم. همچنین اتحادها را معرفی کردیم که پیشنهاد می شود که همه شان را از بر کنید چرا که در خیلی از مباحث مانند گویا کردن کسر که در اینجا بیان شده همچنین مباحث معادله درجه دوم، معادلات گویا و به طور کلی حل معادله و نامعادله و حتی تعیین علامت کاربرد دارد. اگر علاقمند به هر کدام از این مباحث هستید با زدن روی لینک شان می توانید به این مطالب دسترسی پیدا کنید. امیدواریم این مقاله برای شما مفید بوده باشد. اگر تمایل دارید که به صورت جامع و بهمراه نمونه سوالات کنکور و نهایی در سالهای مختلف این مطالب را بیاموزید دوره جبر معادله تابع فرامث را تهیه کنید. لطفا نظرات و پیشنهادات خود را برای کامل کردن مقاله عبارت جبری در قسمت کامنت ها بیان کنید. همچنین اگر سوالی از مبحث جبر داشتید می توانید آن را در قسمت کامنت بپرسید.

جامع ترین آموزش در معرفی عبارات جبری، اتحادها وقوانین ریاضی به زبان جبر

عبارت جبری چیست؟

چطور قوانین ریاضی را با کمک عبارت جبری نشان دهیم؟

چه موقع دو عبارت جبری متشابه اند؟

چه موقع می توان دو عبارت جبری را جمع یا تفریق کرد؟ چگونه؟

چطور می توان دو عبارت جبری را ضرب یا تقسیم کرد؟

چطور می توان عبارت کلامی را تبدیل به یک عبارت جبری کرد؟

چطور مقدار عددی یک عبارت جبری را بدست آوریم؟

تجزیه عبارت جبری: چطور یک عبارت جبری را می توان تجزیه کرد؟

اتحادهای جبری

دیدگاهتان را بنویسید لغو پاسخ

آخرین مطالب وبلاگ

دنباله های عددی

تابع خطی و معادله خط

تابع و دامنه و برد آن

تعیین علامت

عبارت و معادله گویا

معادله درجه دوم

معادله

عبارت جبری

قدرمطلق

دوره ها

دسترسی سریع

دسترسی سریع

مقالات مادر