همه چیز درباره توابع صعودی، نزولی، اکیدا صعودی و اکیدا نزولی
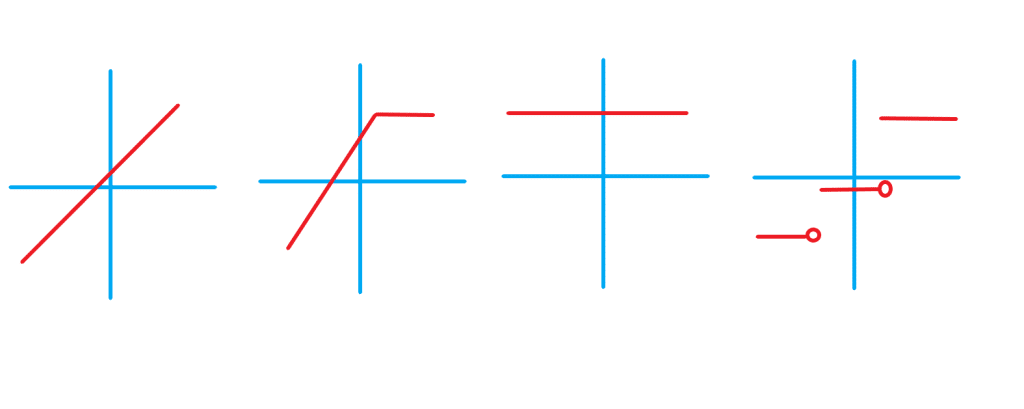
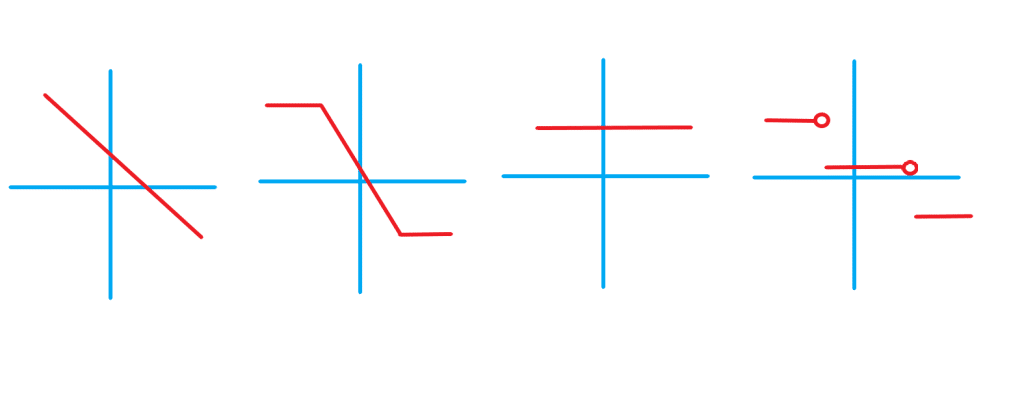
صعودی یا نزولی بودن توابع رفتار تابع را زمانی که ورودی تابع رو به افزایش است می گوید. اگر همزمان با افزایش ورودی مقدار تابع هم افزایش یابد می گوییم تابع صعودی است و اگر با افزایش ورودی مقدار تابع یا همان خروجی تابع کاهش یابد می گوییم تابع نزولی است. در این مقاله همه ی نکات مربوط به صعودی یا نزولی بودن توابع را به صورت خلاصه می خوانید همچنین تفاوت صعودی با صعودی اکید و نزولی با اکیدا نزولی را متوجه می شوید.
تابع صعودی و نزولی چگونه تعریف می شوند؟
- تابع
را در مجموعه
یکنوا گوییم هرگاه در این مجموعه صعودی یا نزولی باشد.
- تابع
را در یک مجموعه ثابت می گوییم اگر برای تمام مقادیر
در این مجموعه مقدار
ثابت باشد با توجه به تعاریف بالا تابع ثابت در یک مجموعه هم صعودی و هم نزولی محسوب می شود.
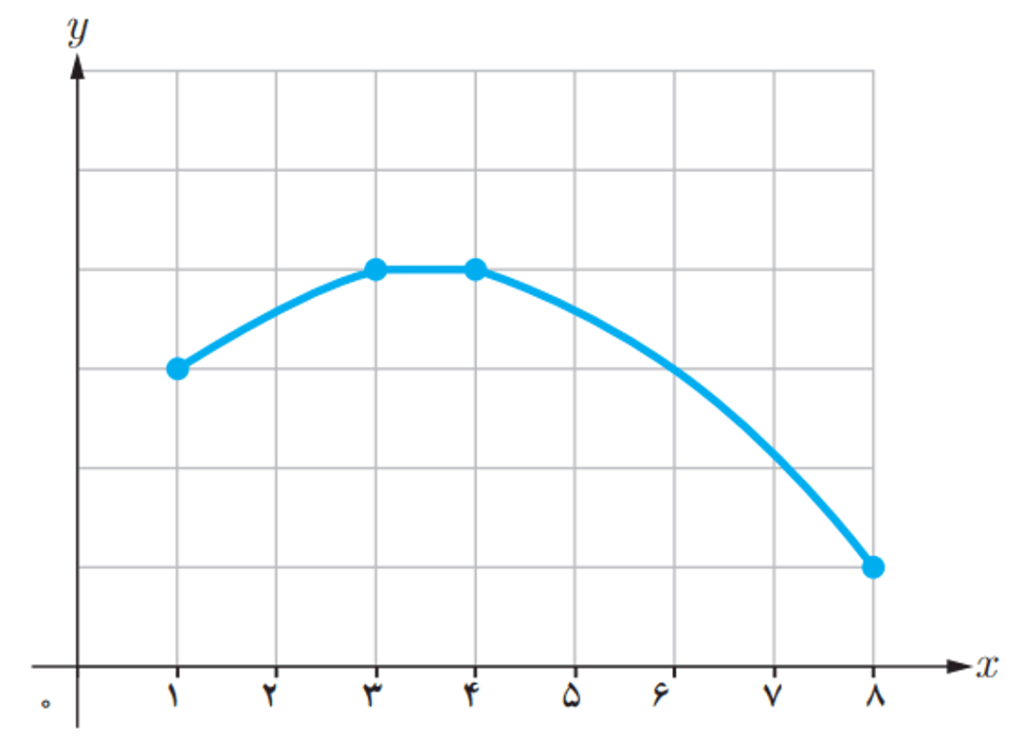
مثال : دامنه تابع که در زیر دیده می شود برابر
می باشد در بازه
همزمان با افزایش
نمودار بالا می رود به همین خاطر به تابع
در بازه
صعودی می گوییم در بازه
مقدار تابع ثابت است. در بازه
همزمان با افزایش
نمودار تابع رو به پایین می رود و به همین منظور تابع
در بازه
نزولی گفته می شود.
توابع اکیدا صعودی و توابع اکیدا نزولی چگونه تعریف می شوند؟
- به تابعی که در یک مجموعه اکیدا صعودی یا اکیدا نزولی باشد اکیدا یکنوا می گوییم.
- نکته: توابع اکیدا یکنوا همواره یکنوا هستند اما برعکس آن الزاما صادق نیست.
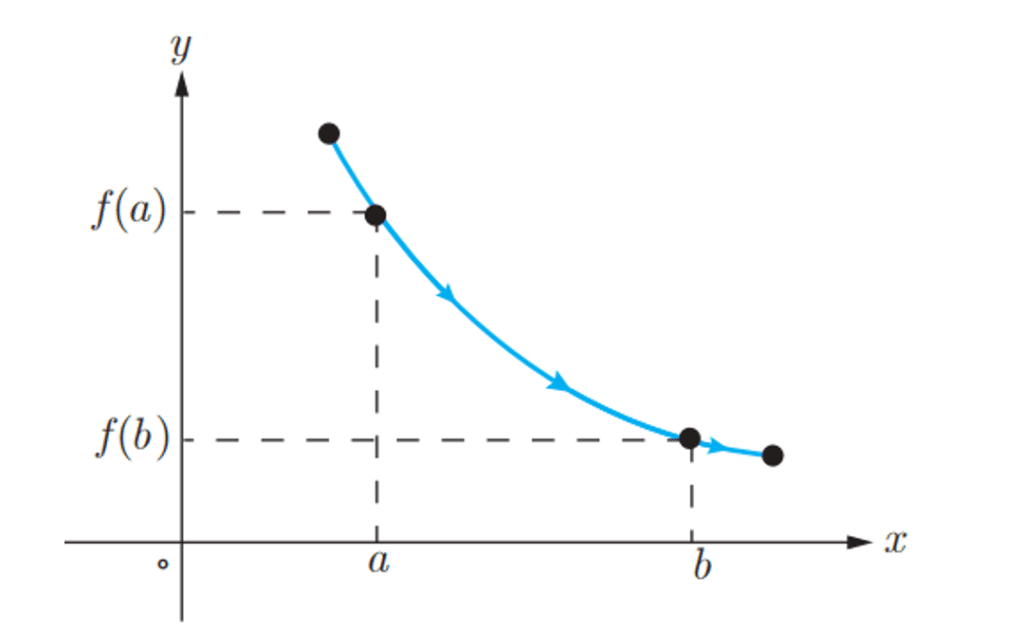
توجه : اگر تابع در یک بازه اکیدا صعودی باشد و
و
متعلق به این بازه باشند. اگر
آنگاه
.
توجه : اگر تابع f در یک بازه اکیدا نزولی باشد و a و b متعلق به این بازه باشند. اگر آنگاه
.
چند نکته درباره ی توابع معروف :
تابع سهمی در راس سهمی و تابع قدرمطلقی در ریشه قدرمطلق مرزی بین قسمت صعودی و قسمت نزولی دارند یعنی در نقطه مرزی از نظر صعودی و نزولی تغییر می کنند.
تابع خطی یا کاملا صعودی اکید است ( وقتی شیب مثبت دارد) یا کاملا نزولی اکید است ( وقتی شیب منفی دارد)
تابع ثابت ( خط افقی ) تابعی هم صعودی و هم نزولی است.
تابع نمایی اگر
صعودی اکید و اگر
نزولی اکید است.
تابع لگاریتمی اگر
صعودی اکید و اگر
نزولی اکید است.
درباره تابع ثابت، سهمی، نمایی و لگاریتمی می توانید در مقاله انواع تابع بیشتر بخوانید.
سوال: اگر ، حدود
را بدست آورید.
جواب: چون پایه ها کمتر از یک هستند پس تابع توانی نزولی است پس داریم:
سوال : تابع در بازه
نزولی است، حداکثر مقدار
چقد راست؟
جواب:
این تابع در صعودی و در
نزولی است.
جمع بندی
در این مقاله به تعریف تابع صعودی ، تابع نزولی ، تابع اکیدا صعودی و تابع اکیدا نزولی پرداخته شده است. همچنین نکاتی درباره انواع تابع و صعودی نزولی بودن آنها بیان شده است. اگر تمایل دارید که به صورت جامع و بهمراه نمونه سوالات کنکور و نهایی در سالهای مختلف این مطالب را بیاموزید دوره جبر معادله تابع فرامث را تهیه کنید. لطفا ما را از نظرات خود درباره مقاله توابع صعودی و نزولی بهره مند کنید.

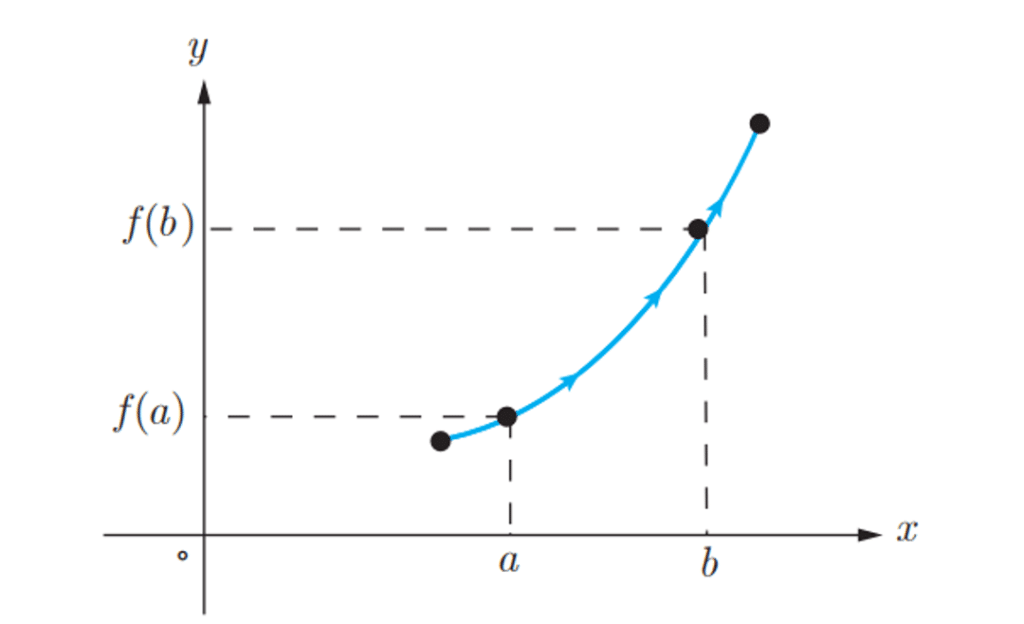
![Rendered by QuickLaTeX.com \[y=x^{2}|x|=\begin{cases} x^{3} & x \ge 0 \\ -x^{3} & x < 0 \end{cases}\]](https://faramath.com/core/ql-cache/quicklatex.com-930cb37d83ce4f1e495def44df6fb3b2_l3.png)

2 پاسخ
سلام خیلی ممنونم که غیر از اینکه همه چیز رو درس دادید مثال هم زدید
سلام عزیزم خوشحالم راضی بودی