ساده ترین و کامل ترین آموزش مبحث تعیین علامت و حل نامعادله درجه اول و دوم

تعیین علامت یعنی اینکه بگوییم یک عبارت جبری در مقادیر متفاوت از متغیرش چه علامتی دارد. در این مقاله آموزش جامعی از نحوه تعیین علامت کردن عبارت چندجمله ای درجه اول و عبارت چندجمله ای درجه دوم می پردازیم. در نهایت آموزش می دهیم که چطور یک عبارت به صورت ضرب و تقسیم چندین عبارت درجه اول و دوم را تعیین علامت کنید. اگر یک آموزش کامل، ساده و جامع برای تعیین علامت می خواهید این مقاله را از دست ندهید. در بخش دوم این مقاله به آموزش نابرابری و نامعادله پرداختیم اگر علاقمند به یادگیری کامل نامعادله هستید حتما به مطالعه این بخش بپردازید. برای یادگیری بهتره این مقاله حتما قبل از خواندن این مقاله مقالات جبر و معادله و معادله درجه دوم را بررسی کنید.

چطور یک عبارت درجه اول را تعیین علامت کنیم؟

چند جمله ای درجه اول $y=ax+b$ برای $x$ های مختلف به صورت زیر تعیین علامت می شود:

اگر $x < -\frac{b}{a}$ آنگاه علامت $y$ مخالف علامت $a$ است.

اگر $x=-\frac{b}{a}$ آنگاه $y$ صفر است.

اگر $x > -\frac{b}{a}$ آنگاه علامت $y$ موافق علامت $a$ است.

مثلا برای چند جمله ای درجه اول $y=5x-2$ داریم:

اگر $x < -\frac{-2}{5}$ آنگاه علامت $y$ مخالف علامت $a=+5$ است. یعنی در بازه $(-\infty , 0.4)$ عبارت $y=5x-2$ منفی است.

اگر $x=-\frac{-2}{5}=+0.4$ آنگاه $y$ صفر است.

اگر $x > -\frac{-2}{5}$ آنگاه علامت $y$ موافق علامت $a=+5$ است. یعنی در بازه $(0.4,+\infty)$ عبارت $y=5x-2$ مثبت است.

چطور یک چند جمله ای درجه دوم را تعیین علامت کنیم؟

چند جمله ای درجه دوم $P(x)=ax^{2}+bx+c$ را در نظر می گیریم که در آن $a$ و $b$ و $c$ اعداد حقیقی اند و $a\neq 0$ است. برای حل معادله $P(x)=0$ باید $\Delta=b^{2}-4ac$ را بدست آوریم. و جواب معادله به صورت $x=\frac{-b\pm\sqrt{\Delta}}{2a}$ بدست می آید. در نتیجه برای جواب ِ معادله درجه دو و تعیین علامت چند جمله ای درجه دوم سه حالت با توجه به علامت $\Delta$ وجود دارد.

حالت اول: اگر $\Delta > 0$ معادله $P(x)=0$ ، دو ریشه حقیقی متمایز $x_{1}$ و $x_{2}$ دارد. فرض می کنیم $x_{1} < x_{2}$ . می توان چند جمله ای را به صورت $P(x)=a(x-x_{1})(x-x_{2})$ نوشت. در این صورت $x$ می تواند در سه بازه قرار داشته باشد:

بازه $x < x_{1}$ : در این بازه علامت $P(x)$ موافق علامت $a$ است.

بازه $x_{1} < x < x_{2}$ : در این بازه علامت $P(x)$ مخالف علامت $a$ است.

بازه $x > x_{2}$ : در این بازه علامت $P(x)$ موافق علامت $a$ است.

حالت دوم: اگر $\Delta=0$ معادله $P(x)=0$ ، یک ریشه مضاعف $x_{1}$ دارد. می توان چند جمله ای را به صورت $P(x)=a(x-x_{1})^{2}$ نوشت. در این حالت به ازای هر $x\neq x_{1}$ ، علامت $P(x)$ موافق علامت $a$ است.

حالت سوم: اگر $\Delta < 0$ معادله، ریشه حقیقی ندارد. در این حالت همواره علامت $P(x)$ موافق علامت $a$ است.

سوال : عبارت $P(x)=x^{2}+4x-5$ را تعیین علامت کنید؟

جواب : ابتدا باید مقدار $\Delta$ را بدست آوریم. می دانیم $\Delta$ از رابطه $\Delta=b^{2}-4ac$ بدست می آید. پس داریم :

$\Delta=b^{2}-4ac$

$=4^{2}-4\times 1 \times(-5)=16+20=36$

حالا باید ریشه ها را از رابطه $x=\frac{-b\pm\sqrt{\Delta}}{2a}$ بدست آوریم. داریم:

$x=\frac{-4+\sqrt{36}}{2}=1$

$x=\frac{-4-\sqrt{36}}{2}=-5$

حالا طبق نکته ای که بالاتر در مورد تعیین علامت عبارت درجه دو گفته شد و با توجه به علامت $a=1$ که مثبت است داریم :

بازه $x < -5$ : در این بازه علامت $P(x)$ موافق علامت $a$ و مثبت است.

بازه $-5 < x < +1$ : در این بازه علامت $P(x)$ مخالف علامت $a$ و منفی است.

بازه $x > +1$ : در این بازه علامت $P(x)$ موافق علامت $a$ و مثبت است.

چطور حاصلضرب چند عبارت درجه اول و دوم را تعیین علامت کنیم؟

در حالتی که یک عبارت شامل حاصل ضرب چندین عبارت جبری درجه یک و درجه دو داشتیم برای تعیین علامت کردن عبارت ابتدا هر معادله را جداگانه با توجه به نکاتی که گفته شد تعیین علامت می کنیم سپس ریشه همه معادلات را از کوچکتر به بزرگتر مرتب می کنیم و در هر بازه ای که ریشه ها ایجاد کردند علامت های همه ی عبارات را در هم ضرب می کنیم تا علامت کل عبارت بدست آید ( طبق قانون اگر تعداد منفی ها زوج بود حاصل مثبت می شود و اگر تعداد منفی ها فرد بود حاصل منفی می شود)

مثال : عبارت زیر را تعیین علامت کنید.

$P(x)=\frac{(x+5)(-2x+6)(x^{2}+4x+4)}{(x^{2}+3x+7)(3x^{2}+5x-2)}$

ریشه عبارت $(x+5)$ را با قرار دادن آن برابر با صفر بدست می آوریم: $x+5=0$ پس $x=-5$ حالا اعداد کمتر از $-5$ مخالف علامت ضریب $x$ یعنی $+1$ است پس در این بازه، عبارت منفی است. اعداد بیشتر از $-5$ موافق علامت ضریب $x$ یعنی $+1$ است پس در این بازه، عبارت مثبت است.

ریشه عبارت $(-2x+6)$ را با قرار دادن آن برابر با صفر بدست می آوریم $-2x+6=0$ پس $x=+3$ حالا اعداد کمتر از $3$ مخالف علامت ضریب $x$ یعنی $-2$ است پس در این بازه، عبارت مثبت است. اعداد بیشتر از $3$ موافق علامت ضریب $x$ یعنی $-2$ است پس در این بازه، عبارت منفی است.

برای بدست آوردن ریشه معادله درجه دو از روابط $\Delta=b^{2}-4ac$ و $x=\frac{-b\pm\sqrt{\Delta}}{2a}$ استفاده می کنیم.

برای عبارت $x^{2}+4x+4$ داریم $\Delta=0$ پس $x=-2$ ریشه مضاعف آن است و می دانیم در این حالت به جز در ریشه به ازای همه مقادیر $x$ عبارت، هم علامت با ضریب $x^{2}$ است.

برای عبارت $x^{2}+3x+7$ داریم $\Delta=-19$ پس این عبارت ریشه ندارد چون علامت $\Delta$ منفی است. و عبارت همواره هم علامت با ضریب $x^{2}$ است.

برای عبارت $3x^{2}+5x-2$ داریم $\Delta=49$ پس این عبارت دو ریشه دارد چون علامت $\Delta$ مثبت است. و ریشه ها برابرند با $x=\frac{-5+7}{6}=\frac{1}{3}$ و $x=\frac{-5-7}{6}=\frac{-12}{6}=-2$ که علامت عبارت بین این دو ریشه مخالف ضریب $x^{2}$ یعنی منفی است و در خارج از این بازه موافق ضریب $x^{2}$ یعنی مثبت است.

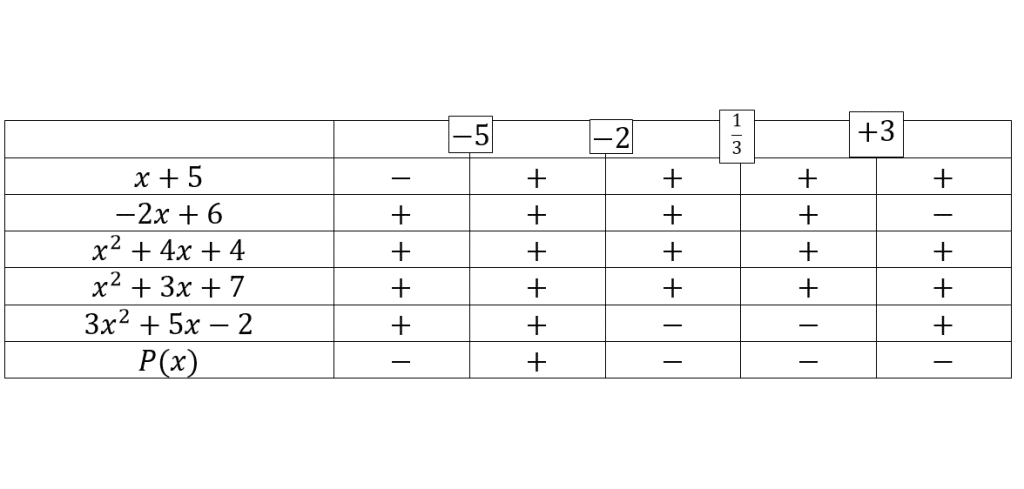
ریشه های همه ی عبارت ها اعداد $-5,-2,\frac{1}{3},+3$

حالا با توجه به جدول زیر علامت $P(x)$ در بازه های مختلف تعیین می شود:

می بینیم با توجه به ضرب علامت ها در هر ستون علامت $P(x)$ محاسبه می شود. بنابراین فقط بین $-5$ و $-2$ مثبت است و در سایر نواحی منفی یا صفر یا تعریف نشده است. (ریشه هایی که مخرج را صفر می کنند یعنی $\frac{1}{3}$ و $-2$ عبارت را بی معنی می کند و عبارت به ازای این اعداد تعریف نشده است)

قوانین نابرابری در ریاضیات چیست؟

هرگاه $a$ و $b$ دو عدد حقیقی باشد، به طوری که $a > b$ ، در این صورت عدد حقیقی مثبتی مانند $p$ هست ؛ به طوری که $a=b+p$ . در این صورت به $a > b$ یک نابرابری می گوییم چرا که $a$ با $b$ برابر نیست. هر نابرابری دارای چندین خاصیت است که در ادامه به برخی از آنها اشاره می کنیم.

خاصیت 1: اگر دو طرف یک نابرابری را با عددی دلخواه مانند $c$ جمع کنیم ، نابرابری همچنان برقرار است؛ یعنی اگر $a > b$ آنگاه $a+c < b+c$ .

خاصیت 2 : اگر دو طرف یک نابرابری را در عدد مثبتی مانند $c$ ضرب کنیم ، نابرابری همچنان برقرار است؛ یعنی اگر $a > b$ آنگاه $ac > bc$ .

خاصیت 3: اگر دو طرف یک نابرابری را در عدد منفی مانند $c$ ضرب کنیم ، نابرابری برعکس می شود؛ یعنی اگر $a > b$ آنگاه $ac < bc$ .

توجه: دو عدد حقیقی $a$ و $b$ فقط یکی از حالت های “ $a$ بزرگتر از $b$ یعنی $a > b$ ” یا ” $a$ کوچکتر از $b$ یعنی $a < b$ ” یا ” $a$ برابر با $b$ یعنی $a=b$ ” را داریم.

اگر $a$ یک عدد نامثبت، یعنی منفی یا صفر باشد، آن را به صورت $a \le 0$ نشان می دهیم. اگر یک عدد نامنفی، مثبت یا صفر باشد، آن را به صورت $a \ge 0$ نشان می دهیم. و اگر یک عدد غیرصفر باشد، مثبت یا منفی است.

برای سه عدد حقیقی $a$ و $b$ و $x$ به طوری که عدد دلخواه $x$ بین اعداد $a$ و $b$ باشد و $a < b$ می نویسیم $a < x < b$ .

اگر $ab < 0$ آنگاه $a$ و $b$ مختلف العلامتند. و اگر $ab > 0$ آنگاه $a$ و $b$ هم علامتند.

اگر $a^{2n}b < 0$ آنگاه $b$ منفی است. و اگر $a^{2n}b > 0$ آنگاه $b$ مثبت است.

نکته: اگر $a^{2} < b^{2}$ آنگاه $| a | < | b |$ . طبق آنچه در مورد قدرمطلق می دانیم می توان نتیجه گرفت:

اگر هر دو مثبت باشند داریم: $a < b$ . مثلا $3^{2} < 5^{2}$ در نتیجه $3 < 5$ و

اگر هر دو منفی باشند داریم: $a > b$ . مثلا $(-3)^{2} < (-5)^{2}$ آنگاه $-5 < -3$ و

اگر یکی مثبت و دیگری منفی باشد حتما عدد مثبت بزرگتر از عدد منفی است. مثلا در $3^{2} < (-5)^{2}$ در نتیجه $-5 < 3$ و در $(-3)^{2} < 5^{2}$ در نتیجه $-3 < 5$ .

در ادامه به آموزش حل نامعادله به کمک تعیین علامت می پردازیم.

چطور یک نامعادله درجه اول را حل کنیم؟

در مقاله مربوط به جبر خواندیم که که می توان عبارات کلامی را به عبارت جبری تبدیل کرد تا یک دیدگاه ریاضی نسبت به آن داشته باشیم. حالا اگر یک عبارت مانند ” یکی بیشتر از دو برابر یک عدد از عدد هفت بزرگتر است” داشته باشیم و بخواهیم محدوده ی مجاز آن عدد را محاسبه کنیم، ابتدا باید این عبارت را به صورت عبارت جبری بنویسیم. داریم: $2x+1 > 7$ به این نابرابری ، نامعادله یک مجهولی درجه اول می گوییم. حالا برای اینکه محدوده مجاز $x$ را بدست آوریم مانند آنچه در مقاله معادله خواندیم عمل می کنیم. داریم:

$2x > 7-1 \,\,\rightarrow\,\,2x > 6$

$\rightarrow \,\,\,x > \frac{6}{2} \,\,\rightarrow \,\,x > 3$

سوال : مجموعه جواب نامعادله های زیر را بدست آورید.

$3(x-1) \ge 2x+1 \,\,\,\rightarrow \,\,3x-3 \ge 2x-1$

$\rightarrow \,\,\, 3x-2x \ge -1+3 \,\,\, \rightarrow \,\,\, x \ge 2$

$\frac{2}{3}(x+7)-\frac{x}{4} \le \frac{1}{2}(3-x)+\frac{x}{6}$

$\overset{\times 6}{\rightarrow}\,\,\,4x+28 \ge 9-3x+x$

$\rightarrow \,\,\,4x+3x-x \ge 9-28$

$\rightarrow \,\,\, 6x \ge -19 \,\,\,\rightarrow \,\,\, x \ge \frac{-19}{6}$

یک مدل دیگر از سوالات وجود دارد که یک عبارت بین دو عبارت قرار دارد در این حالت دو نامعادله را حل می کنیم و بازه های حاصل را اشتراک می گیریم. برای مثال اگر بخواهیم نامعادله ی $-5 \le 3x-2 \le 7$ را حل کنیم باید دو نامعادله ی $-5 \le 3x-2$ و $3x-2 \le 7$ را حل کنیم سپس از جواب این دو نامعادله اشتراک می گیریم.

گام اول : باید نامعادله $-5 \le 3x-2$ را حل کنیم.

$-5 \le 3x-2 \,\,\,\overset{+2}{\rightarrow}\,\,\,-5+2 \le 3x$

$\rightarrow \,\,\,-3 \le 3x \,\,\, \overset{\div 3}{\rightarrow}\,\,\, -1 \le x$

گام دوم: باید نامعادله $3x-2 \le 7$ را حل کنیم.

$3x-2 \le 7 \,\,\,\overset{+2}{\rightarrow} \,\,\, 3x \le 7+2$

$\rightarrow \,\,\, 3x \le 9 \,\,\, \overset{\div 3}{\rightarrow}\,\,\, x \le 3$

گام سوم: باید بین دو جواب اشتراک بگیریم:

$\{-1 \le x\} \cap \{x \le 3\}$

$= (-\infty , 3]\cap [-1,+\infty)=[-1,3]$

چطور یک نامعادله درجه دوم را حل کنیم؟

در حالتی که یک عبارت درجه دوم در یک نامساوی وجود داشته باشد باید همه ی عبارت را به یک سمت نامساوی ببریم تا در گام بعد با کمک آنچه در این مقاله خواندیم به حل نامساوی بپردازیم.

بعنوان مثال برای حل نامعادله $x^{2}+5x+7 < -3x^{2}-12x+35$ گام های زیر را طی می کنیم:

گام اول: عبارت یک سمتِ نامساوی را به سمت دیگر می بریم. می دانیم اگر یک عبارت یا عدد را از یک سمت نامساوی یا تساوی به سمت دیگر ببریم علامت آن عبارت یا عدد عوض می شود ( از مثبت به منفی و از منفی به مثبت تغییر می کند) بنابراین داریم:

$x^{2}+5x+7+3x^{2}+12x-35 < 0$

$\rightarrow \,\,\, 4x^{2}+17x-28 < 0$

گام دوم : ریشه ی معادله ی به دست آمده را بدست می آوریم. یکی از جامع ترین روش های بدست آرودن ریشه معادله درجه دوم که در مقاله مربوطه آمده روش دلتا است. با توجه به این روش داریم:

$\Delta=17^{2}+4\times 4\times 28=289+448=737$

$\rightarrow x=\frac{-17\pm \sqrt{737}}{8}$

$\rightarrow \,\,\, x=5.51 \,\,,\,\, x=1.27$

گام سوم: با توجه به قوانین تعیین علامت از آنجا که علامت ضریب $x^{2}$ مثبت است بنابراین جواب این نامعادله برابر با $1.27 < x < 5.51$ .

همه ی نکات تعیین علامت را در جدول زیر می توانید ببینید:

جمع بندی

در این مقاله به آموزش تعیین علامت کردن یک عبارت درجه یک و عبارت درجه دو یا سهمی پرداختیم. در میانه راه به آموزش تعیین علامت یک عبارت شامل چندین عبارت درجه یک و دو پرداختیم. و با آموزش نابرابری و نامعادله این آموزش را به پایان رساندیم. تعیین علامت یکی از مباحث عبارات جبری است. اگر علاقه مند به یادگیری مطالب مربوط به جبر و معادله هستید به مقاله مربوط به آنها مراجعه کنید. امیدواریم از این آموزش بهره لازم را برده باشید. اگر تمایل دارید که به صورت جامع و بهمراه نمونه سوالات کنکور و نهایی در سالهای مختلف این مطالب را بیاموزید دوره جبر معادله تابع فرامث را تهیه کنید. اگر پرسش یا نظری در مورد این آموزش تعیین علامت و نامعادله دارید لطفا در قسمت کامنت ها بیان کنید.

ساده ترین و کامل ترین آموزش مبحث تعیین علامت و حل نامعادله درجه اول و دوم

چطور یک عبارت درجه اول را تعیین علامت کنیم؟

چطور یک چند جمله ای درجه دوم را تعیین علامت کنیم؟

چطور حاصلضرب چند عبارت درجه اول و دوم را تعیین علامت کنیم؟

قوانین نابرابری در ریاضیات چیست؟

چطور یک نامعادله درجه اول را حل کنیم؟

چطور یک نامعادله درجه دوم را حل کنیم؟

دیدگاهتان را بنویسید لغو پاسخ

آخرین مطالب وبلاگ

دنباله های عددی

تابع خطی و معادله خط

تابع و دامنه و برد آن

تعیین علامت

عبارت و معادله گویا

معادله درجه دوم

معادله

عبارت جبری

قدرمطلق

دوره ها

دسترسی سریع

دسترسی سریع

مقالات مادر