کامل ترین آموزش در مورد تابع ، دامنه و برد آن، تشخیص آن و انواع نمایش تابع

تابع یک رابطه بین چند متغیر است که یکی از آنها وابسته و بقیه مستقل اند. در این مقاله به تعریف تابع و دامنه و برد و هم دامنه آن می پردازیم همچنین انواع نمایش تابع را با ذکر مثال هایی آموزش می دهیم. نحوه تشخیص اینکه در هر کدام از نمایش های رابطه یعنی نمودار پیکانی، نمودار مختصاتی ، زوج مرتب و ضابطه تابع چطور تشخیص دهیم که رابطه مورد نظر تابع هست یا نه را در این مقاله آموزش داده ایم. اگر می خواهید تعریف تابع و دامنه و برد آن را بدانید و انواع نمایش تابع را بیاموزید، این مقاله را از دست ندهید. اگر علاقمند به یادگیری انواع تابع هستید می توانید به مقاله انواع توابع رجوع کنید. اگر می خواهید بدانید نمودار توابع مختلف را رسم کنید و انتقال نمودارهای توابع را بیاموزید به مقاله رسم نمودار توابع رجوع کنید. اما پیشنهاد می کنیم قبل از همه ی این مقالات حتما به خواندن مقاله حاضر بپردازید تا پیش نیازهای لازم برای آموزش موضوعات مربوط به تابع را بدانید.

تابع چیست؟ دامنه و برد آن چگونه تعریف می شود؟

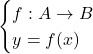
تابع $f$ از مجموعه $A$ به مجموعه $B$ ، رابطه ای بین این دو مجموعه است که در آن به هر عضو از $A$ دقیقا یک عضو از $B$ نسبت داده می شود. $A$ را دامنه تابع و $B$ را هم دامنه تابع می نامند برد تابع زیرمجموعه ای از هم دامنه است. برای نمایش این تابع می نویسیم : $\begin{cases} f:A\rightarrow B \\ y=f(x) \end{cases}$ که $y=f(x)$ را ضابطه تابع می گوییم.

همچنین می توان تابع را همچون ماشینی در نظر گرفت که یک ورودی را دریافت می کند و در ازای آن یک خروجی تحویل میدهد. ورودی ها از دامنه داده می شوند و خروجی ها به برد تعلق دارند و برای هر ورودی دقیقا ً یک خروجی وجود دارد (البته ممکن است چند ورودی مختلف خروجی یکسانی داشته باشند) اگر $x$ عنصری داخواه از دامنه $f$ و $y$ نمایش خروجی نظیر آن باشد، $x$ را متغیر مستقل و $y$ را متغیر وابسته می نامیم. در این صورت می نویسیم $y=f(x)$

نکته: برای مشخص بودن یک تابع باید دامنه، هم دامنه و دستور یا قاعده ای که نحوه ارتباط بین اعضای دامنه و اعضای هم دامنه را نشان می دهد معلوم باشد.

هم دامنه تابع را می توان هر مجموعه دلخواهی شامل برد تابع در نظر گرفت. برد تابع همان مقادیر تابع به ازای همه ی اعضای دامنه تابع است.

اگر تابع را با $f$ نمایش دهیم، آنگاه دامنه تابع را با $D_{f}$ و برد آن را با $R_{f}$ نمایش می دهیم. اگر بخواهیم بگوییم $y$ تابعی از $x$ است می توانیم بگوییم $y=f(x)$ .

انواع نمایش تابع: مختصاتی، ضابطه ای، زوج مرتبی و پیکانی

رابطه ها را می توان با زوج مرتب، نمودار پیکانی و نمودار مختصاتی نشان داد. برای اینکه هر کدام از این نمایش ها نشانگر تابع باشند باید در تعریف تابع صدق کنند. در ادامه به بررسی دقیق و کاملی از هر کدام از نمودار پیکانی، مختصاتی و زوج مرتب می پردازیم.

نمایش زوج مرتبی تابع

اگر یک جفت عدد را در پرانتز قرار دهیم و ترتیب آنها برایمان اهمیت داشته باشد (یعنی نتوانیم این دو عدد را جابجا کنیم) یک زوج مرتب داریم. در هر زوج مرتب به عضو اول مولفه اول و به عضو دوم مولفه دوم می گوییم . اگر یک مجموعه شامل چند زوج مرتب داشته باشیم که رابطه ی بین دو کمیت را به ما نشان دهند، این مجموعه را با حروف کوچک انگلیسی نشان می دهیم و آن را رابطه می نامیم.

زوج مرتب یک جفت هستند که ترتیب در آنها مهم است به همین دلیل به آن زوج مرتب می گویند. در زوج مرتب $(a,b)$ به $a$ مولفه اول و به $b$ مولفه دوم می گوییم.

اگر بخواهیم تابع $f$ را به صورت زوج مرتب نشان دهیم می توانیم به صورت نمادین عبارت زیر را در نظر بگیریم:

$f=\{(x_{1},y_{1}),(x_{2},y_{2}), … , (x_{n},y_{n})\}$

در این نمایش از تابع به مجموعه $\{x _{1},x_{2},…,x_{n}\}$ دامنه تابع می گویند که این موضوع را به صورت $D_{f}=\{x_{1},x_{2},…,x_{n}\}$ نشان می دهند. همچنین برد تابع را به صورت $R_{f}=\{y_{1},y_{2},…,y_{n}\}$ نشان می دهیم.

نکته مهم: شرط اینکه یک رابطه ی زوج مرتبی تابع باشد این است که در این رابطه اگر دو زوج مرتب مولفه اول ِ یکسان داشتند، حتما مولفه دوم شان نیز یکسان باشد.

نمایش پیکانی تابع

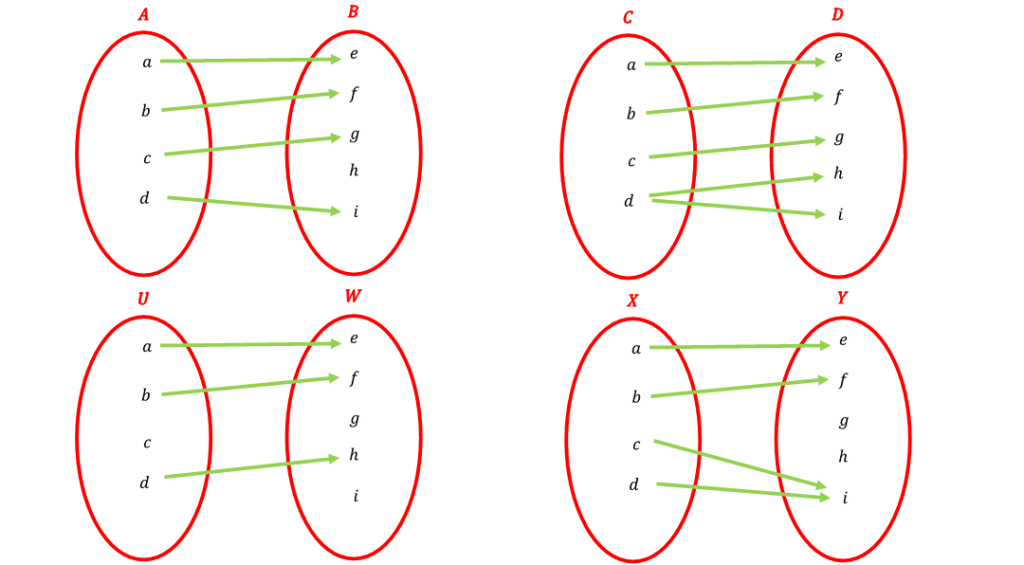
برای اینکه یک رابطه را به صورت پیکانی نمایش دهیم کافی است که ورودی های رابطه را در بیضی سمت چپ و خروجی ها را در بیضی سمت راست قرار دهیم و هر ورودی که با توجه به رابطه منجربه خروجی یا خروجی هایی می شود با پیکان به آن خروجی یا خروجی ها وصل کنیم. به شکل های زیر که هر کدام رابطه ای را با نمودار پیکانی نشان می دهند توجه کنید:

نکته مهم: یک رابطه وقتی تابع است که در نمودار پیکانی آن از هر عضو ورودی یک و دقیقا یک پیکان خارج شود و به سمت خروجی ها برود. در نتیجه در شکل های بالا رابطه ای که از $A$ به $B$ یک تابع است. رابطه ای که از $X$ به $Y$ تعریف شده نیز یک تابع است. اما رابطه ای که از $C$ به $D$ و از $U$ به $W$ تعریف شده تابع نیست. رابطه ای که از $C$ به $D$ تعریف شده به این دلیل تابع نیست که از $d$ دو پیکان خارج شده است و رابطه ای که از $U$ به $W$ تعریف شده تابع نیست چون از $c$ هیچ پیکانی خارج نشده است.

توجه کنید که برای تشخیص اینکه یک نمودار پیکانی، تابع را نشان می دهد یا نه فقط به قسمت ورودی نگاه می کنیم و قسمت خروجی اصلا برایمان اهمیت ندارد.

نکته: اگر یک نمودار پیکانی تابع را نشان دهند. به ورودی های آن “دامنه” تابع می گوییم و به خروجی های آن “هم دامنه” می گوییم از بین خروجی های موجود آنهایی که پیکان به سمت شان نشانه رفته “برد” تابع هستند.

نمایش مختصاتی تابع

اگر بخواهیم یک رابطه را روی محورهای مختصات نمایش دهیم کافی است ورودی های رابطه را روی محور طول ها و خروجی های رابطه را روی محور عرض ها نشان دهیم. سپس برای هر ورودی بررسی کنیم که منجربه چه خروجی هایی می شود و با توجه به آن نقاطی را در صفحه مختصات نشان دهیم. به این ترتیب یک سری نقطه در صفحه مختصات با توجه به رابطه ی مورد نظر ایجاد می شود. در نتیجه ما یک نمایش مختصاتی از رابطه ی مورد نظر رسم کرده ایم.

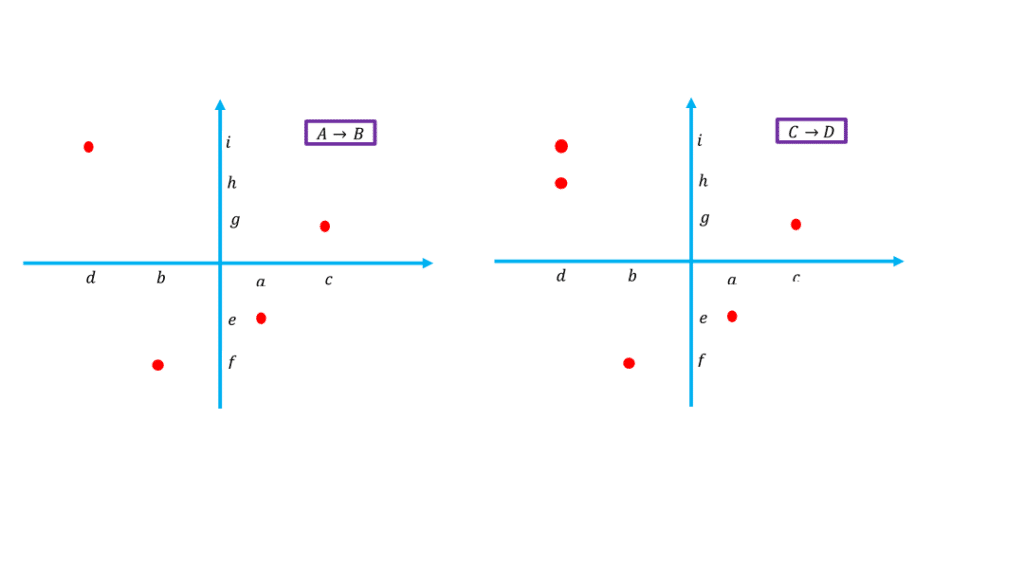
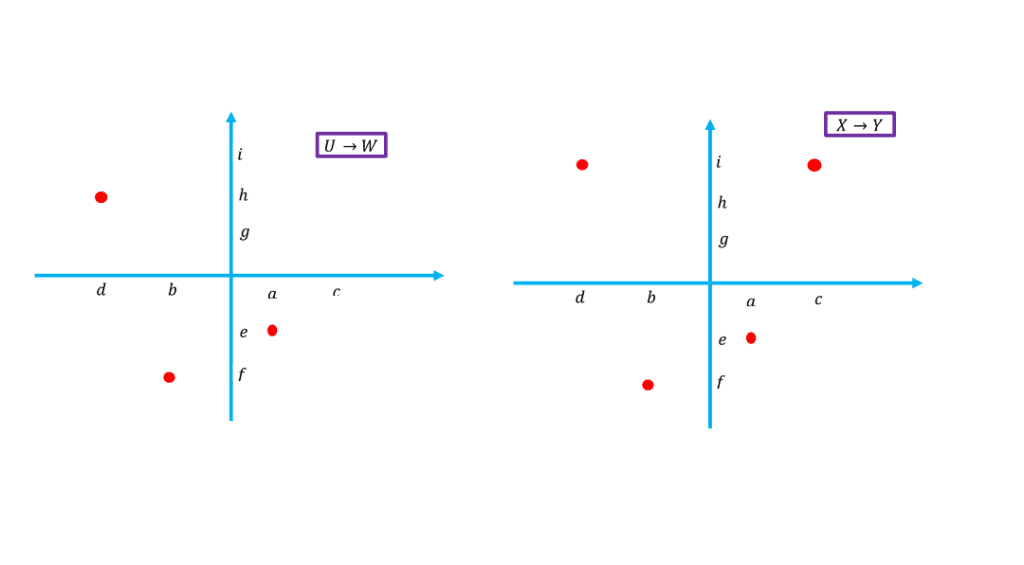
در ادامه نمودار مختصاتی روابطی که در قسمت قبل با نمودار پیکانی نشان داده شده بودند را می بینیم:

در حالتی که یک رابطه در صفحه مختصات نشان داده شده برای اینکه بفهمیم آن رابطه تابع هست یا نه کافیست که خطوط مختلفی موازی با محور عرض ها رسم کنیم اگر این خطوط منحنی یا نقاط رابطه را در دو نقطه یا بیشتر قطع کردند می گوییم رابطه تابع نیست اما اگر خطوط موازی با محور عرض ها منحنی یا نقاط رابطه را حداکثر در یک نقطه قطع کند آنگاه رابطه مورد نظر یک تابع است.

به تصویر منحنی تابع روی محور طول ها ” دامنه تابع ” و به تصویر منحنی تابع روی محور عرض ها ” برد تابع ” می گویند.

توجه: در نمودار پیکانی می دانیم چه مقادیری ورودی رابطه هستند و اگر یک عدد به عنوان ورودی معرفی شده باشد اما خروجی ای برای آن تعریف نشده باشد آنگاه می گوییم که آن رابطه تابع نیست. اما در نمودار مختصاتی این موضوع قابل بررسی نیست. و تعریفی که از تشخیص تابع در نمودار مختصاتی کردیم این مورد را بررسی نمی کند. مثل رابطه ای که از $U\rightarrow W$ تعریف شده است با توجه به نمودار پیکانی تابع نیست اما با توجه به نمودار مختصاتی تابع هست. که در حقیقت این رابطه تابع نیست.

بنابراین اگر اطلاعاتی از ورودی های تابع دارید و نمودار مختصاتی را دادند مطمئن شوید که برای همه ی ورودی ها، یک خروجی تعریف شده باشد.

نمایش ضابطه ای یک تابع

در این نمایش از یک رابطه ی جبری برای بیان ارتباط بین ورودی ها و خروجی های یک تابع استفاده می شود. در این نوع نمایش برای اینکه بفهمیم ضابطه مورد نظر تابع هست یا نه کافی است مطمئن شویم که به ازای هر ورودی، یک و دقیقا یک خروجی وجود دارد.

مثلا برای اینکه بررسی کنیم که روابط جبری $y=x^{2}$ و $y^{2}=x$ تابع هستند یا نه باید مراحل زیر را انجام دهیم:

$y=x^{2}\,\,:\,\, x_{1}=x_{2}$

$\rightarrow \,\,\, x_{1}^{2}=x_{2}^{2}\,\,\,\rightarrow\,\,\,y_{1}=y_{2}$

پس رابطه $y=x^{2}$ یک تابع است.

$y^{2}=x\,\,\,\rightarrow \,\,\,y=\pm\sqrt{x}\,\,:\,\,x_{1}=x_{2}$

$\rightarrow \,\,\, y_{1}=y_{2} \,\,\,or\,\,\,y_{1}=-y_{2}\,\,\,\rightarrow\,\,\, y_{1}\neq y_{2}$

پس رابطه $y^{2}=x$ یک تابع نیست. چون به ازای ورودی های برابر الزاما خروجی های برابر ایجاد نمی کند.

چطور تشخیص دهیم یک رابطه تابع هست یا نه؟

برای اینکه مشخص کنیم که یک رابطه تابع هست یا نه سه روش داریم:

1- نمودار تابع را رسم کنیم وبررسی کنیم آیا هر خط موازی محور عرض ها نمودار تابع را حداکثر در یک نقطه قطع می کند؟ اگر بله پس تابع است.

2-بررسی کنیم به صورت ضابطه ای به ازای هر $x$ یک مقدار برای $y$ بدست می آید ؟ اگر فقط یک مقدار بدست آید تابع است اگر دو یا چند مقدار برای $y$ بدست آید رابطه تابع نیست.

3-با یک مثال نقض نشان دهیم به ازای یک $x$ دو یا چند $y$ بدست می آید این روش فقط برای اثبات تابع نبودن کاربرد دارد.

چطور صفرهای یک تابع را بدست آوریم؟

برای هر تابع $f$ جواب های معادله ی $f(x)=0$ را در صورت وجود صفرهای تابع $f$ می نامیم. به عبارت دیگر، صفرهای تابع $f$ آن مقادیری از $x$ در دامنه $f$ هستند که به ازای آنها $f(x)$ برابر صفر می شود. اگر نمودار $f(x)$ را رسم کنیم صفرهای $f$ طول نقاط تلاقی نمودار با محور $x$ هاست.

اگر $\alpha$ و $\beta$ صفرهای تابع $f(x)=ax^{2}+bx+c$ باشند می توان نوشت:

$ax^{2}+bx+c=a(x-\alpha)(x-\beta)$

نکته: برخی از معادلات را می توان با یک تغییر متغیر مناسب به یکی از انواع معادلاتی که می شناسیم تبدیل کرد و پس از حل آن و با رجوع به تغییر متغیر مقادیر مجهول اصلی معادله اولیه را بدست آورد

نکته : اگر $x=\alpha$ یکی از صفر های تابع $f(x)$ باشد می توان نوشت $f(x)=g(x)(x-\alpha)$ که $g(x)$ حاصل تقسیم $f(x)$ بر $x-\alpha$ است.

جمع بندی

در این مقاله به آموزش تابع تعریف تابع دامنه و برد تابع و رابطه ی برد با هم دامنه تابع پرداختیم. همچنین انواع نمایش تابع را آموزش دادیم و به تعریف و آموزش زوج مرتب، نمودار پیکانی، نمودار مختصاتی و ضابطه ی یک رابطه و تشخیص اینکه در هر کدام از این موارد رابطه، تابع هست یا نه پرداختیم. این موارد پیش نیازهای مبحث تابع است که در مقاله تعریف تابع و انواع نمایش های آن به آن پرداختیم. اگر می خواهید در ادامه در مورد انواع توابع بخوانید و علم کاملی در مورد این که چه نوع توابعی وجود دارند و دامنه و برد هر کدام چیست ضابطه و نمودار آنها چیست به مقاله انواع توابع رجوع کنید. همچنین اگر می خواهید در مورد نمودار توابع و انتقال نمودارها بدانید به مقاله نمودار توابع مراجعه کنید. اگر تمایل دارید که به صورت جامع و بهمراه نمونه سوالات کنکور و نهایی در سالهای مختلف این مطالب را بیاموزید دوره جبر معادله تابع فرامث را تهیه کنید. لطفا نظرات خود را در مورد مقاله تعریف تابع و انواع نمایش و دامنه و برد آن در قسمت کامنت ها بیان کنید.

کامل ترین آموزش در مورد تابع ، دامنه و برد آن، تشخیص آن و انواع نمایش تابع

تابع چیست؟ دامنه و برد آن چگونه تعریف می شود؟

انواع نمایش تابع: مختصاتی، ضابطه ای، زوج مرتبی و پیکانی

چطور تشخیص دهیم یک رابطه تابع هست یا نه؟

چطور صفرهای یک تابع را بدست آوریم؟

دیدگاهتان را بنویسید لغو پاسخ

آخرین مطالب وبلاگ

دنباله های عددی

تابع خطی و معادله خط

تابع و دامنه و برد آن

تعیین علامت

عبارت و معادله گویا

معادله درجه دوم

معادله

عبارت جبری

قدرمطلق

دوره ها

دسترسی سریع

دسترسی سریع

مقالات مادر