کامل ترین آموزش رسم نمودار توابع و تبدیل نمودار توابع

رسم نمودار توابع به درک بهتر تابع و بررسی بهترِ دامنه و برد آن و صعودی یا نزولی بودن تابع کمک می کند. در این مقاله در ایتدا نمودار انواع توابع را نشان دادیم سپس با نکاتی بیان کردیم که چه موقع نمودار یک تابع در راستای محور عرض ها یا طول ها جابجا می شود و با اینکار چه تغییری در ضابطه تابع بوجود می آید همچنین چه زمانی تابع منبسط یا منقبض می شود؟ چه تغییری در ضابطه تابع بوجود آمده که تابع منبسط یا منقبض می شود. اگر می خواهید جواب همه ی این سوالات را بدانید و با صرف کمترین زمان همه ی نکات مربوط به رسم توابع را بدانید این مقاله را از دست ندهید.

چطور نمودار توابع خطی، سهمی، درجه سوم، قدرمطلقی، گویا، رادیکالی، نمایی و لگاریتمی را رسم کنیم؟

شکل توابع معروف را در ادامه می بینید:

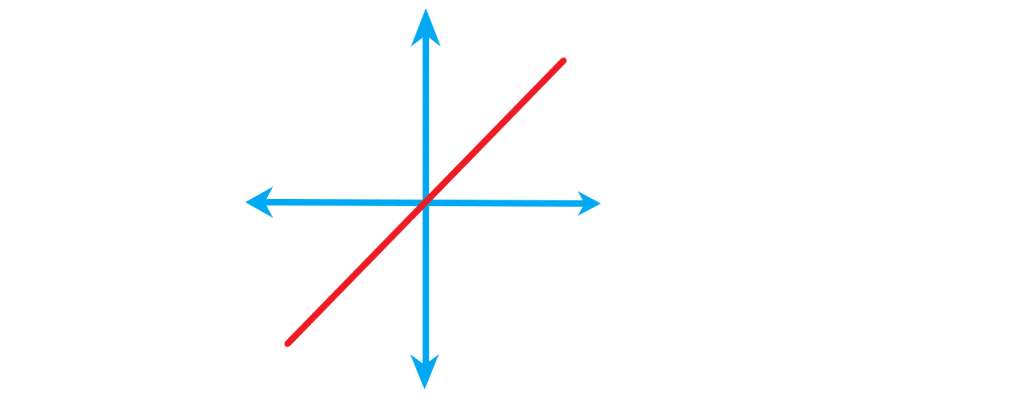
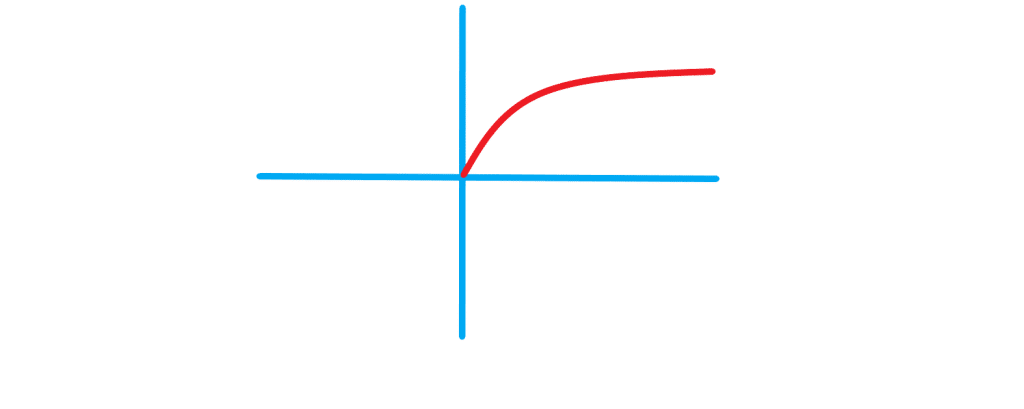
در شکل زیر تابع همانی ساده تزین حالت تابع خطی $y=x$ را می بینید:

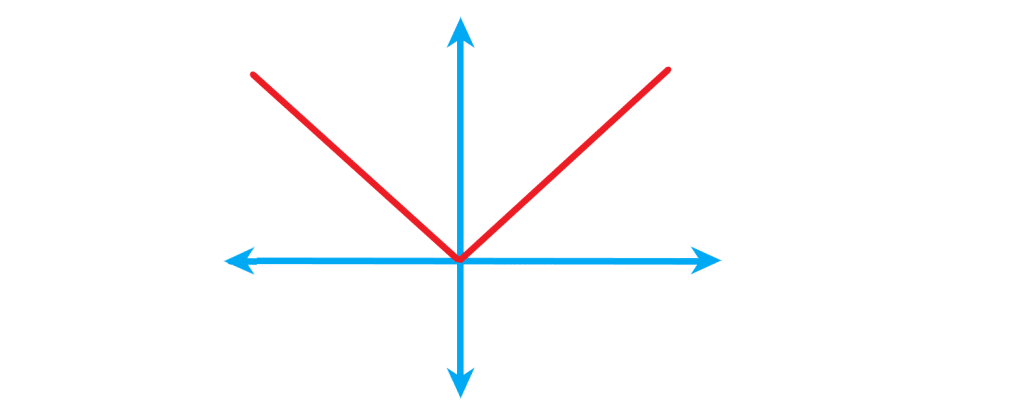
تابع قدر مطلق : شکل تابع $f(x)=|x|$ به صورت زیر می باشد:

تابع $y=x^{2}$ را در ادامه می بینید. این تابع ساده ترین حالت سهمی یا تابع درجه دوم است.

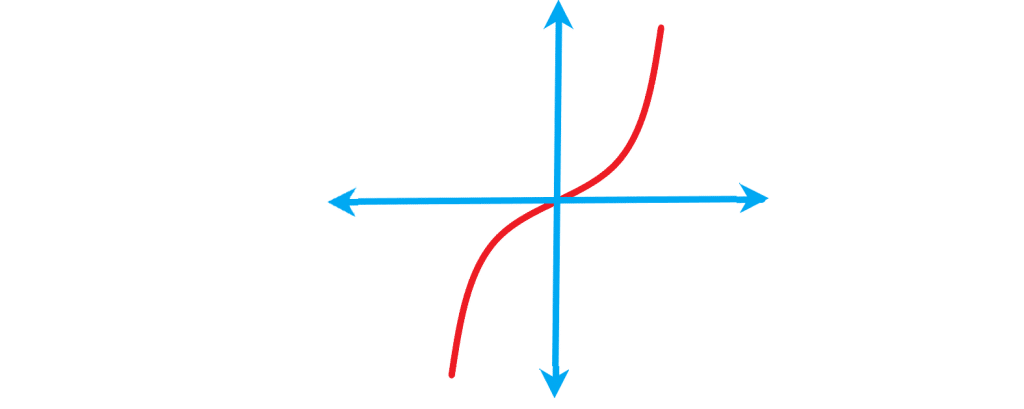
تابع $y=x^{3}$ را در زیر می توانید ببینید:

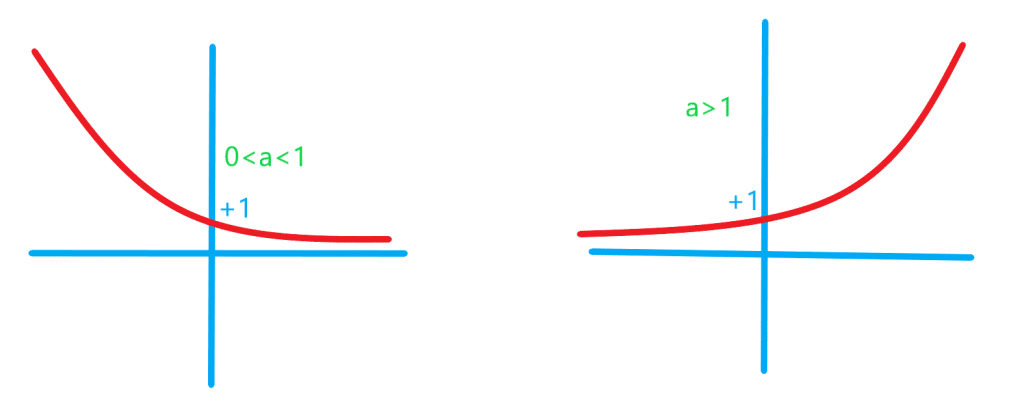
شکل زیر تابع $y=a^{x}$ تابع نمایی است را نشان می دهد:

شکل زیر تابع لگاریتمی $y=\log_{a}{x}$ را نشان می دهد:

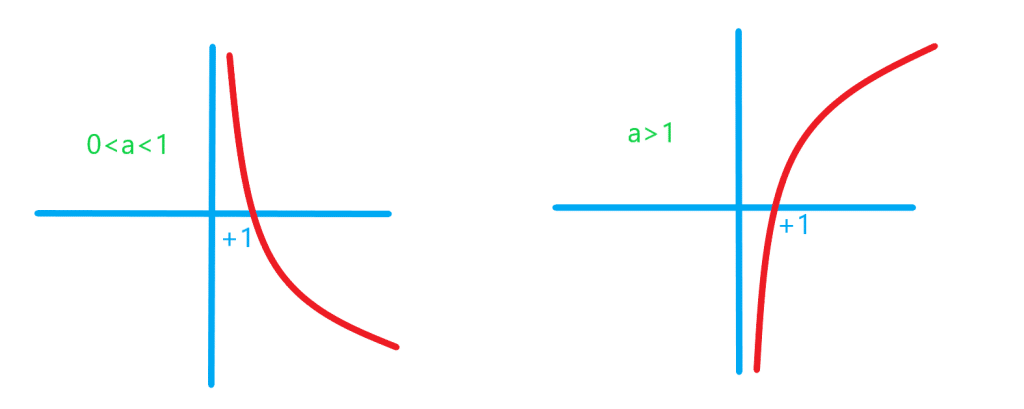
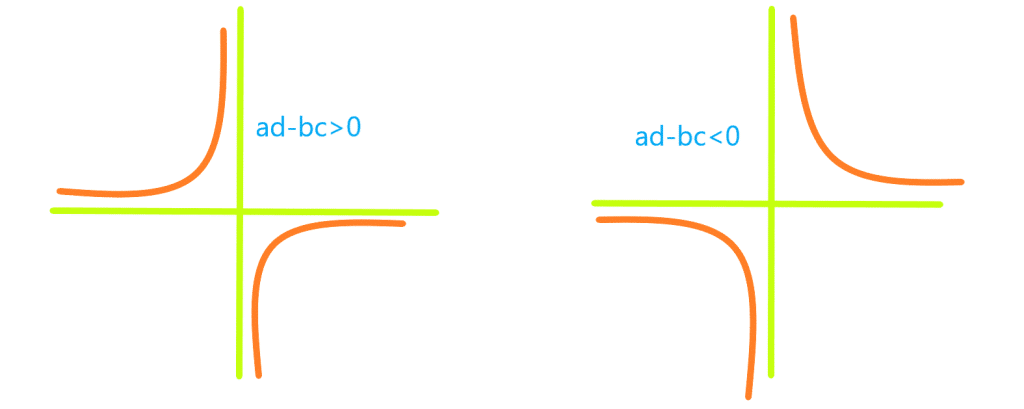
تابع زیر حالت کلی تابع گویا $y=\frac{ax+b}{cx+d}$ را نشان می دهد:

تابع زیر ساده ترین حالت تابع رادیکالی $y=\sqrt{x}$ را نشان می دهد:

همه ی نکات درباره انتقال، انقباض و انبساط افقی و عمودی نمودار توابع

در این بخش می آموزیم توابعی که در بخش قبل شکل شان را یاد گرفتیم چطور روی محور حرکت دهیم و آنها را باز یا بسته کنیم.

انقباض و انبساط عمودی نمودار تابع

نمودار $y=kf(x)$ تغییرات زیر را نسبت به نمودار $y=f(x)$ دارد:

اگر $k > 0$ نمودار $y=kf(x)$ را می توان با انبساط یا انقباض نمودار $y=f(x)$ در امتداد محور ها به دست آورد.

اگر $k < 0$ ابتدا نمودار $f$ نسبت به محور $x$ ها قرینه می شود، سپس با ضریب $|k|$ به طور عمودی منبسط یا منقبض می شود.

برای رسم نمودار $y=kf(x)$ کافی است عرض نقاط نمودار تابع $y=f(x)$ را در $k$ ضرب کنیم. در شکل های زیر نمودار تابع $y=kf(x)$ برای دو حالت $k > 1$ و $0 < k < 1$ رسم شده است.

اگر $k > 1$ باشد نمودار $y=kf(x)$ از انبساط عمودی نمودار $y=f(x)$ حاصل می شود و اگر

$0 < k < 1$ باشد نمودار $y=kf(x)$ از انقباض عمودی نمودار $y=f(x)$ بدست می آید.

*برای رسم نمودار تابع $y=-f(x)$ کافی است قرینه نمودار تابع ضابطه $y=f(x)$ را نسبت به محور طول ها رسم کنیم. شکل زیر نمودار قرینه ی یک تابع را نشان می دهد:

*دامنه تابع $y=kf(x)$ همان دامنه تابع $y=f(x)$ است، اما برد آنها لزوما یکسان نیست.

*همچنین چون ریشه های معادله $f(x)=0$ و $kf(x)=0$ یکسان است بنابراین محل تلاقی نمودار توابع $f$ و $kf$ با محور $x$ ها یکسان است.

*در حالت کلی اگر $(x_{0},y_{0})$ یک نقطه از نمودار تابع $y=f(x)$ باشد و تابع $g$ به صورت $g(x)=kf(x)$ تعریف شده باشد، آنگاه: $g(x_{0})=kf(x_{0})=ky_{0}$ . بنابراین $(x_{0},ky_{0})$ یک نقطه از نمودار تابع $g$ متناظر با نقطه $(x_{0},y_{0})$ از نمودار تابع $f$ است.

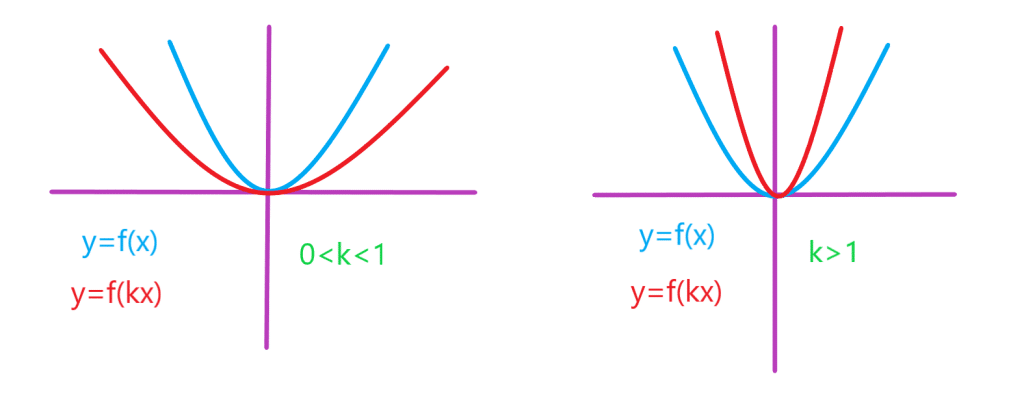
انقباض و انبساط افقی تابع

رسم نمودار $f(kx)$ با استفاده از نمودار $f(x)$ :

برای رسم نمودار تابع $y=f(kx)$ ، کافی است طول نقاط نمودار تابع $y=f(x)$ را در $\frac{1}{k}$ ضرب کنیم.

اگر $k > 0$ نمودار $y=f(kx)$ را می توان با انبساط یا انقباض نمودار $y=f(x)$ در امتداد محور طول ها به دست آورد.

اگر $k < 0$ ابتدا نمودار $f$ نسبت به محور $y$ ها قرینه می شود، سپس با ضریب $| \frac{1}{k} |$ به طور افقی منبسط یا منقبض می شود.

*دامنه تابع $y=f(kx)$ با دامنه تابع $y=f(x)$ الزاما یکسان نیست ولی برد تابع $y=f(kx)$ همان برد $y=f(x)$ است.

*در شکل های زیر نمودار $y=f(kx)$ برای دو حالت $k > 1$ و $0 < k < 1$ رسم شده است:

همانطور که میبینیم شکل ها نتایج زیر را نشان می دهند:

*اگر $k > 1$ باشد نمودار $y=f(kx)$ از انقباض افقی نمودار $y=f(x)$ در راستای محور $x$ ها حاصل می شود و اگر $0 < k < 1$ باشد نمودار $y=f(kx)$ از انبساط افقی نمودار $y=f(x)$ بدست می آید.

*اگر طول نقاط تابع $y=f(x)$ را قرینه کنیم نقاط تابع $y=f(-x)$ بدست می آیند. بنابراین نمودار تابع $y=f(-x)$ قرینه نمودار تابع $y=f(x)$ نسبت به محور $y$ هاست.برای مثال می توانید به شکل زیر توجه کنید:

*در حالت کلی اگر $(x_{0},y_{0})$ یک نقطه دلخواه از نمودار تابع $y=f(x)$ باشد و تابع $g$ به صورت $g(x)=f(kx)$ تعریف شده باشد، آنگاه $g(\frac{x_{0}}{k})=f(k\frac{x_{0}}{k})=f(x_{0})=y_{0}$ . بنابراین نقطه $(\frac{x_{0}}{k},y_{0})$ یک نقطه از نمودار تابع و متناظر با نقطه $(x_{0},y_{0})$ از نمودار تابع $f$ است.

انتقال عمودی نمودارتابع

با داشتن نمودار تابعی مانند $f(x)$ ، می توان نمودار تابع $f(x)+k$ را با انتقال نمودار $f(x)$ به اندازه $k$ واحد در امتداد محور $y$ ها به دست آورد. اگر $k > 0$ باشد انتقال در جهت مثبت و اگر $k <0$ باشد انتقال در جهت منفی خواهد بود.

نکته : اگر $(x_{0},y_{0})$ یک نقطه از نمودار تابع $y=f(x)$ باشد و تابع $g$ به صورت $g(x)=f(x)+k$ تعریف شده باشد، آنگاه $g(x_{0})=f(x_{0})+k=y_{0}+k$ . بنابراین نقطه $(x_{0},y_{0}+k)$ از نمودار تابع $g$ متناظر با نقطه $(x_{0},y_{0})$ از نمودار $f$ است.

انتقال افقی نمودار تابع

برای رسم نمودار تابع $f(x+k)$ کافی است نمودار تابع $f(x)$ را $k$ واحد در امتداد محور $x$ ها انتقال دهیم. اگر $k >0$ باشد انتقال در جهت منفی و اگر $k < 0$ باشد انتقال در جهت مثبت خواهد بود.

برای رسم نمودار $y=f(x+k)$ اگر $k > 0$ باشد کافی است نمودار تابع $f(x)$ را $k$ واحد در راستای افقی به سمت چپ انتقال دهیم و برای $k < 0$ این انتقال به سمت راست انجام می شود.

نکته : اگر $(x_{0},y_{0})$ یک نقطه از نمودار تابع $y=f(x)$ باشد و تابع $h$ به صورت $h(x)=f(x+k)$ تعریف شده باشد، آنگاه $h(x_{0}-k)=f(x_{0}-k+k)=f(x_{0})=y_{0}$ . بنابراین نقطه $(x_{0}-k,y_{0})$ از نمودار تابع $h$ متناظر با نقطه $(x_{0},y_{0})$ از نمودار $f$ است.

نکته: برای رسم نمودار $y=f(x+k)$ اگر $k > 0$ باشد کافی است نمودار تابع $f(x)$ را $k$ واحد در راستای افقی به سمت چپ انتقال دهیم و برای $k < 0$ این انتقال به سمت راست انجام می شود.

نمودار قدرمطلق تابع

برای رسم نمودار $y=|f(x)|$ کافی است نمودار $y=f(x)$ را رسم کنیم و در قسمت هایی که نمودار $f$ زیر محور $x$ هاست، قرینه نمودار $f$ را نسبت به محور $x$ ها رسم کنیم.

چند نکته جامع درباره ی انتقال نمودار توابع

چند نکته جامع درباره ی رسم نمودار توابع و انتقال نمودار توابع را در ادامه می بینید:

قرینه نمودار نسبت به محورها و نیمساز ها و نتیجه ی این تبدیل ها

اگر تابعی نسبت به $x=k$ متقارن باشد رابطه $f(x)=f(k-x)$ برقرار است.
قرینه نمودار نسبت به $y=x$ یعنی جای $x$ و $y$ را در معادله منحنی عوض کنیم
برای رسم قرینه نمودار نسبت به مبدا، اول نمودار را نسبت به $x$ و بعد نسبت به $y$ قرینه می کنیم.

رسم نمودار $g(x)=f(ax+b)$ از روی نمودار $f$

برای رسم نمودار $g(x)=f(ax+b)$ از روی نمودار $f$ داریم:

روش اول : اول $b$ واحد به چپ بعد تقسیم طول نقاط بر $a$

روش دوم : تقسیم طول نقاط بر $a$ بعد انتقال به چپ به اندازه $\frac{b}{a}$

توجه: روش اول ساده تر است.

دامنه و برد توابع بعد از انتقال ها:

اگر دامنه و برد تابع $f$ بصورت $D_{f}=[a,b]$ و $R_{f}=[c,d]$ باشد پس :

*دامنه و برد تابع $g(x)=f(x)+k$ عبارت است از $D_{g}=[a,b]$ و $R_{g}=[c+k,d+k]$

*دامنه و برد تابع $h(x)=f(x+k)$ عبارت است از $D_{h}=[a-k,b-k]$ و $R_{h}=[c,d]$

*دامنه و برد تابع $g(x)=kf(x)$ اگر $k >0$ عبارت است از $D_{g}=[a,b]$ و $R_{g}=[kc,kd]$
*دامنه و برد تابع $g(x)=kf(x)$ اگر $k <0$ عبارت است از $D_{g}=[a,b]$ و $R_{g}=[kd,kc]$

*دامنه و برد تابع $g(x)=f(kx)$ اگر $k >0$ عبارت است از $D_{g}=[\frac{a}{k},\frac{b}{k}]$ و $R_{g}=[c,d]$
*دامنه و برد تابع $g(x)=f(kx)$ اگر $k <0$ عبارت است از $D_{g}=[\frac{b}{k},\frac{a}{k}]$ و $R_{g}=[kd,kc]$

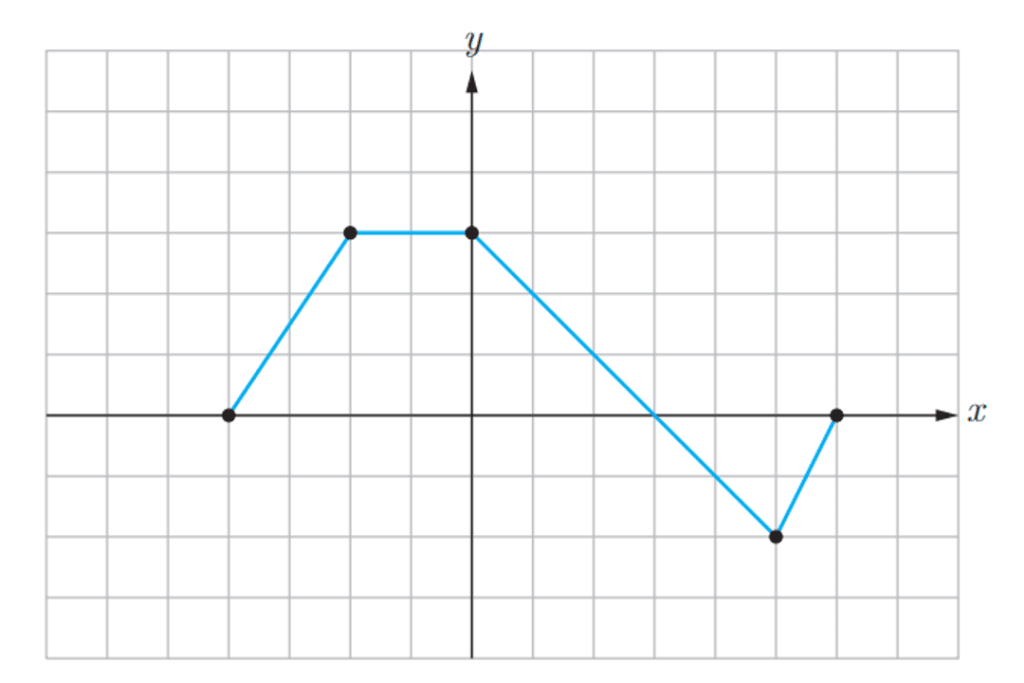
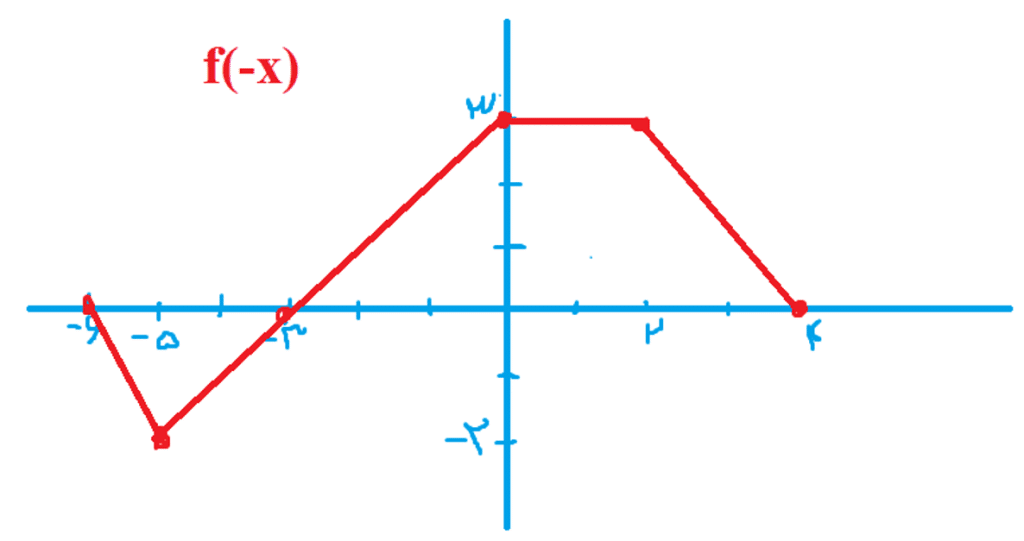
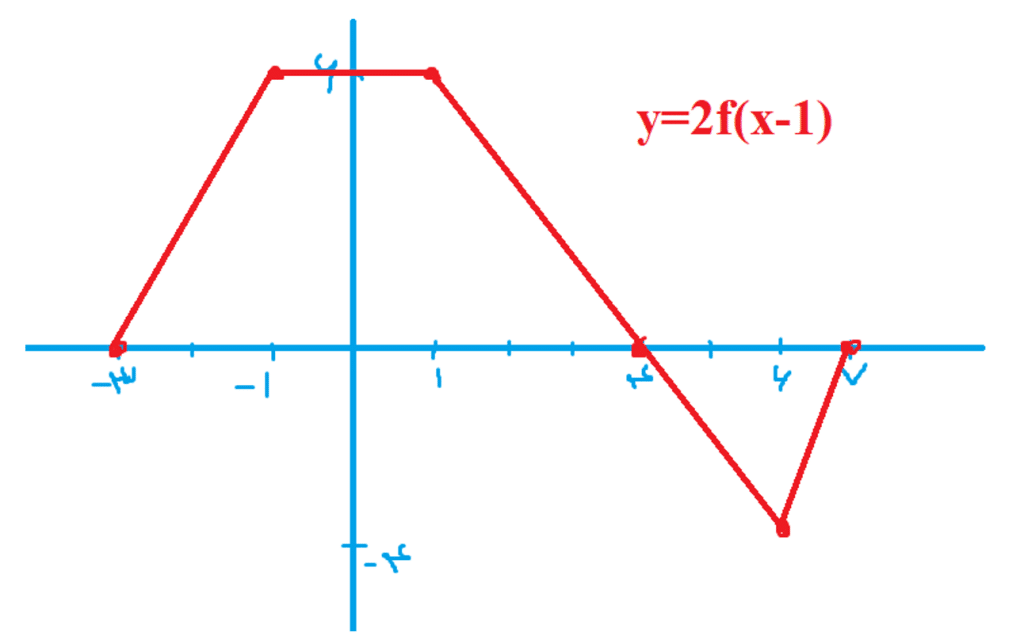
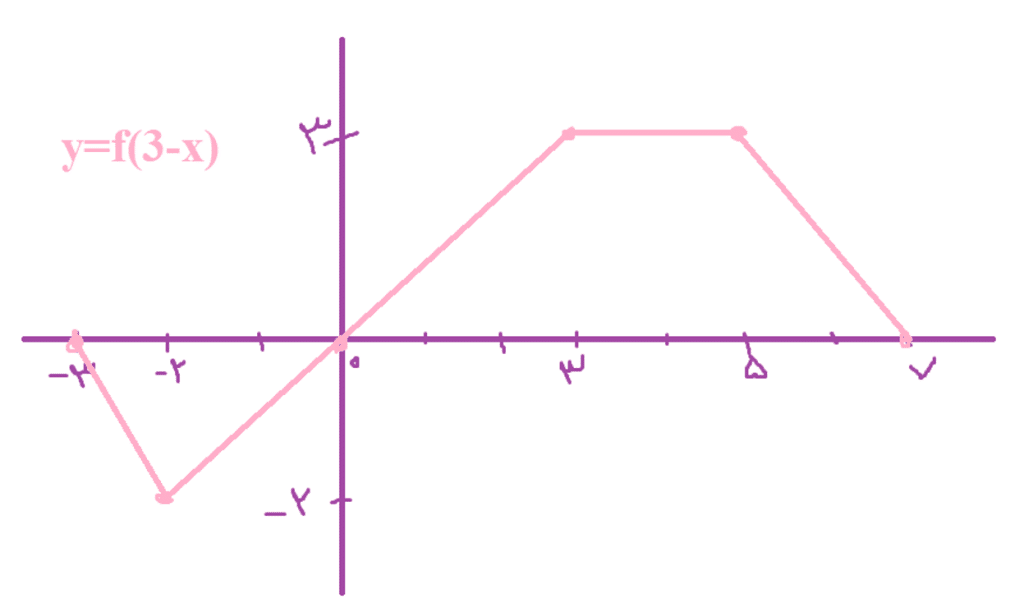
سوال: نمودار تابع $f$ داده شده نمودار هر یک از توابع را رسم کنید.

$y=f(-x)$

$y=2f(x-1)$

$y=-f(x)+2$

$y=f(2x-1)$

$y=f(3-x)$

جواب های این سوال را که با توجه به آنچه در متن آمده رسم شده در شکل های زیر می توانید ببینید:

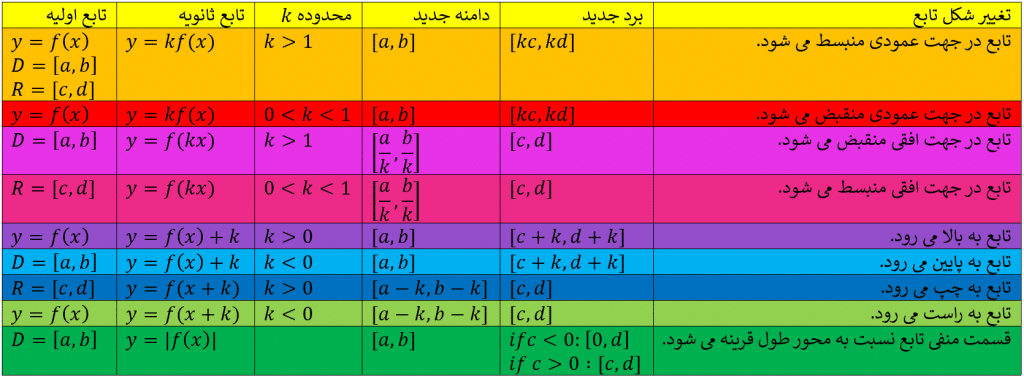
همه ی نکات این مقاله را به طور خلاصه می توانید در جدول زیر ببینید:

جمع بندی

در این مقاله نمودار انواع توابع معروف مثل نمودار سهمی ، قدرمطلق، تابع درجه سه، تابع لگاریتم و تابع نمایی را نشان دادیم سپس با نکاتی که در این مقاله گفته شد آموختیم که با کمک این توابع چطور توابع جدیدی بسازیم چطور در جهت محور عرض ها یک تابع را جابجا کنیم و اگر این کار را کردیم چه تغییری در ضابطه تابع بوجود می آید و بالعکس اگر تغییری در ضابطه تابع بوجود بیاید چه تغییری در نمودار تابع ایجاد می شود آیا در جهت محور عرض ها جابجا می شود ؟ آیا در جهت محور طول ها جابجا می شود؟ اگر بله این جابجایی ها به چه اندازه است؟ آیا نمودار تابع منقبض یا منبسط می شود؟ شرایط انقباض یا انبساط چیست؟ جواب همه ی این سوالات را در این مقاله آموختیم امیدوارم بهره لازم را از خواندن این مقاله برده باشید. اگر تمایل دارید که به صورت جامع و بهمراه نمونه سوالات کنکور و نهایی در سالهای مختلف این مطالب را بیاموزید دوره جبر معادله تابع فرامث را تهیه کنید. لطفا ما را از نظرات ارزشمند خود درباره مقاله رسم نمودار توابع و تبدیل نمودار توابع بهره مند کنید.

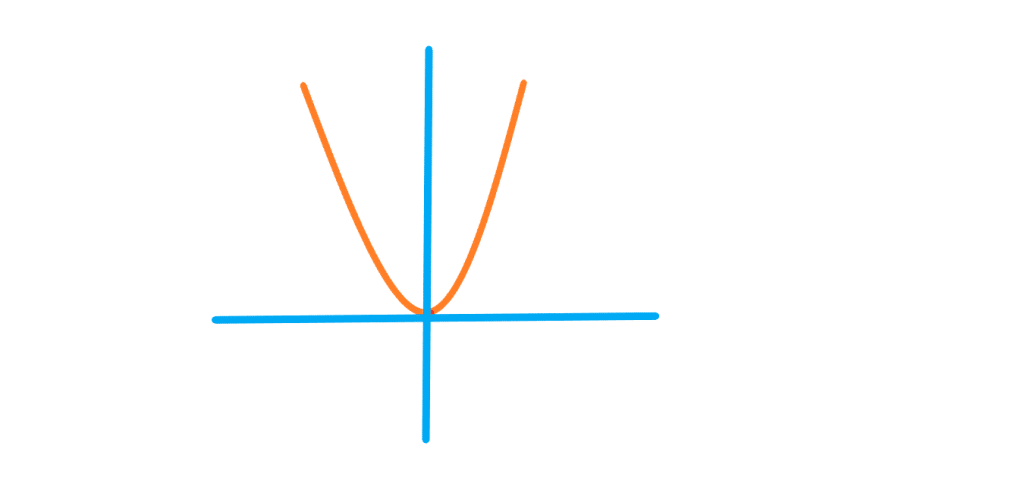
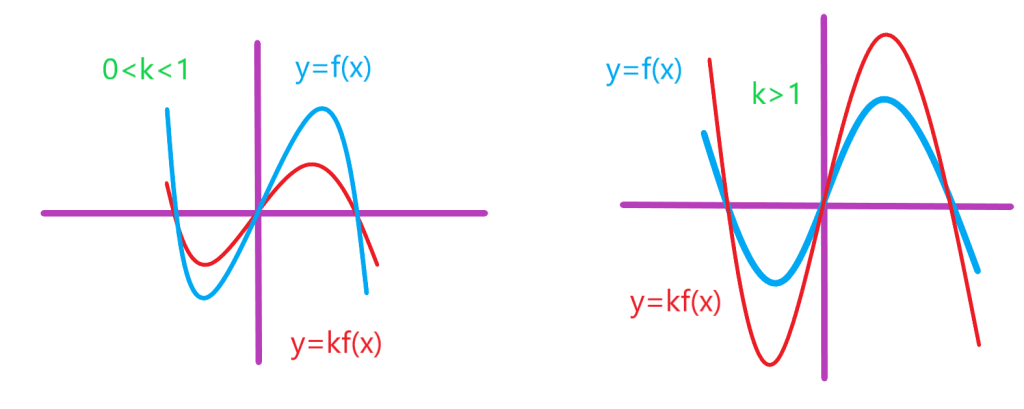
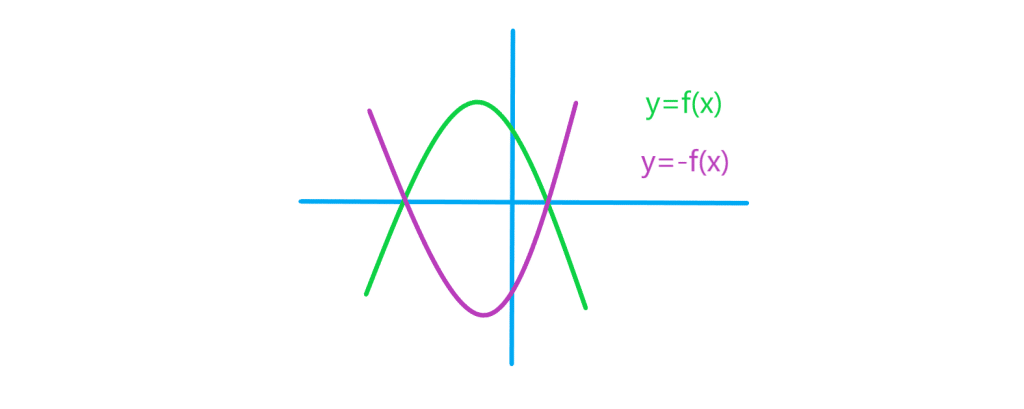
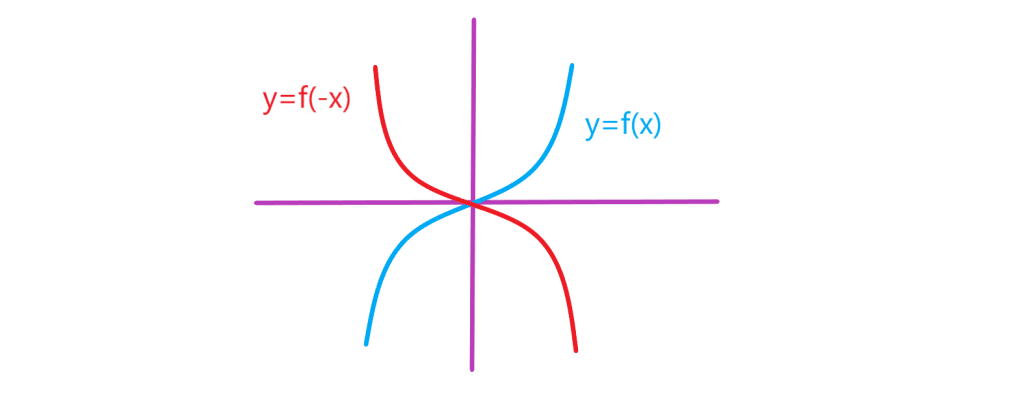
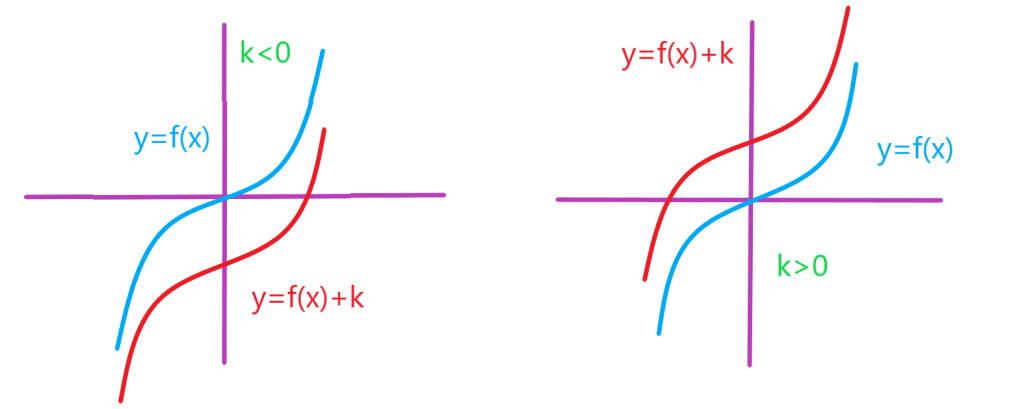
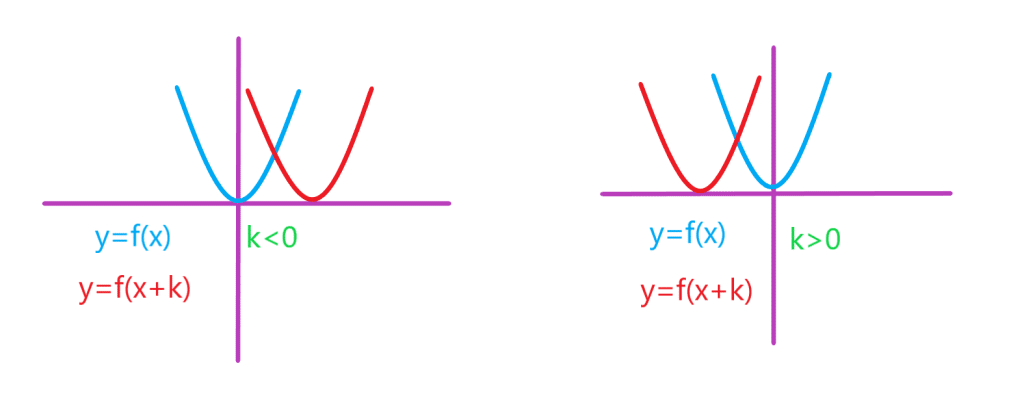
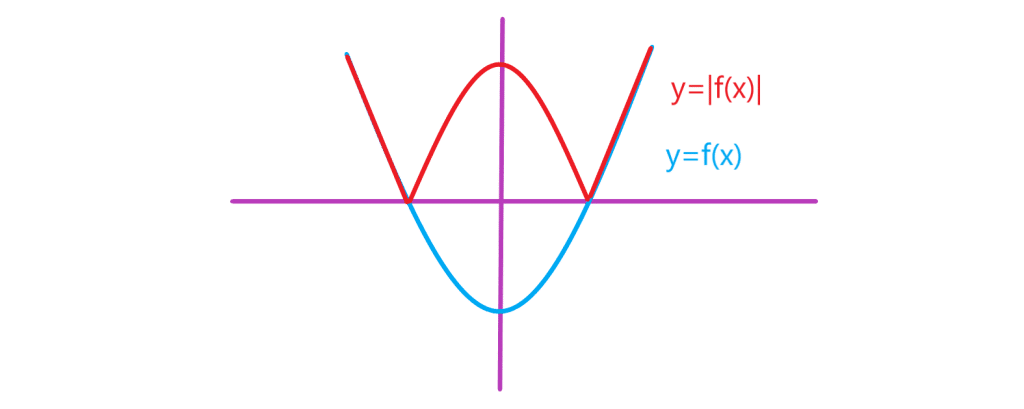
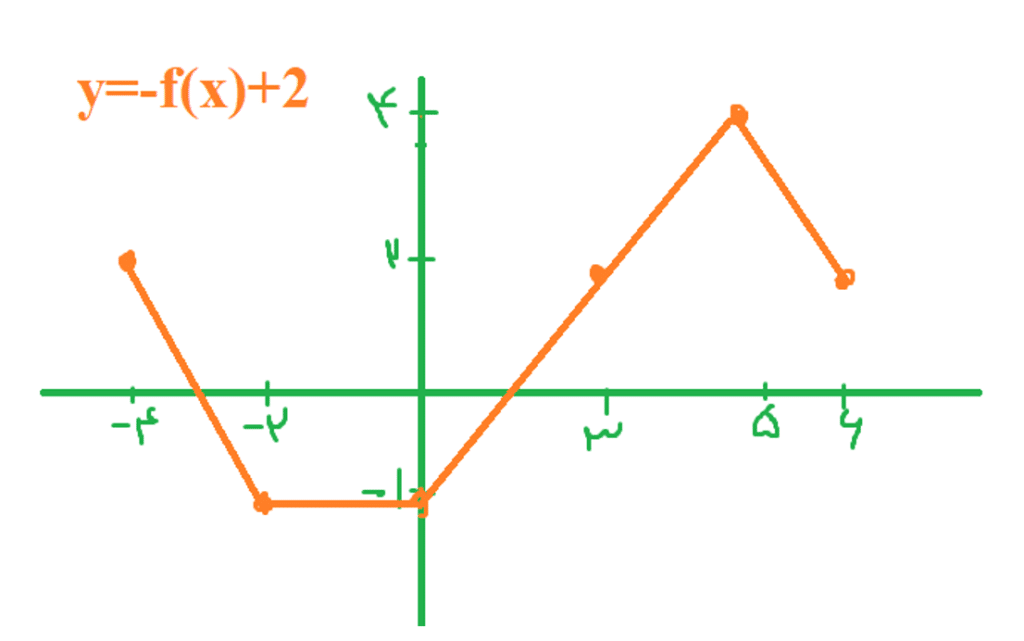
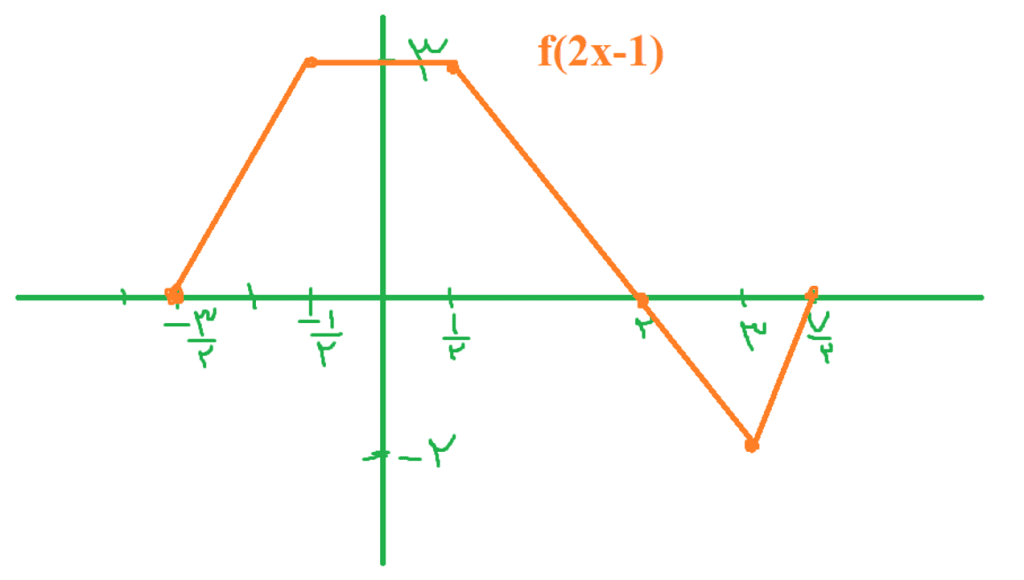
2 پاسخ

امیرحسین گفت:

آوریل 16, 2025 در 07:05

آخیش که همه شکل ها رو گفتید مرسی که همه نکات انتقال نمودار رو گفتید عجب مثالی عجب مثالی دمتون گرم

پاسخ
1. ریحانه حسینی گفت:
  
  آوریل 16, 2025 در 17:25
  
  سلامت باشی عزیزم خوشحالن برات مفید بوده سعی کردیم که از مثال های جامعی استفاده کنیم ممنونم توجه کردی
  
  پاسخ

کامل ترین آموزش رسم نمودار توابع و تبدیل نمودار توابع

چطور نمودار توابع خطی، سهمی، درجه سوم، قدرمطلقی، گویا، رادیکالی، نمایی و لگاریتمی را رسم کنیم؟

همه ی نکات درباره انتقال، انقباض و انبساط افقی و عمودی نمودار توابع

چند نکته جامع درباره ی انتقال نمودار توابع

2 پاسخ

دیدگاهتان را بنویسید لغو پاسخ

آخرین مطالب وبلاگ

دنباله های عددی

تابع خطی و معادله خط

تابع و دامنه و برد آن

تعیین علامت

عبارت و معادله گویا

معادله درجه دوم

معادله

عبارت جبری

قدرمطلق

دوره ها

دسترسی سریع

دسترسی سریع

مقالات مادر