همه چیز درباره توابع یک به یک و وارون ِ یک تابع
وارون یک تابع از جابجایی ورودی و خروجی تابع بدست می آید. در این مقاله ابتدا به بیان نحوه بدست آوردن وارون یک تابع پرداختیم بعد توابع یک به یک را تعریف کردیم و بررسی کردیم که چرا وارون برخی توابع خودشان تابع هستند و وارون برخی توابع خودشان تابع نیستند. همچنین در این مقاله بیان شده است که چطور می توان با محدود کردن دامنه یک تابع غیر یک به یک آن را تبدیل به یک تابع وارون پذیر کرد. اگر می خواهید همه نکات توابع یک به یک و تابع وارون را بدانید این مقاله را از دست ندهید.
وارون یک تابع چگونه تعریف می شود؟
اگر رابطه بین دو مجموعه به صورت زوج های مرتب داده شده باشد رابطه ای را که از جابجایی دو مولفه هر زوج مرتب رابطه بدست می آید وارونِ آن رابطه می نامیم.
اگر یک تابع باشد وارون آن را با
نمایش می دهیم و به صورت زیر تعریف می کنیم :
اگر تابع باشد آن گاه
را وارون پذیر ( معکوس پذیر) و
را وارون تابع
می نامیم.
توجه: را نباید با
اشتباه گرفت.
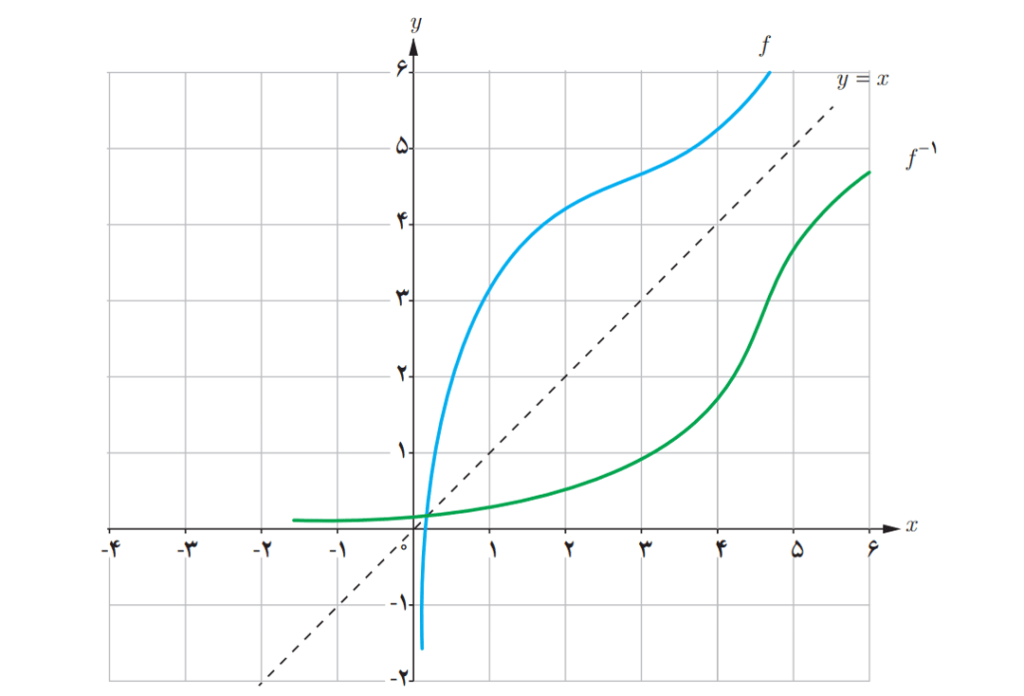
نکته: نمودار تابع و تابع وارون
آن نسبت به خط
(نیمساز ربع اول و سوم ) قرینه اند.
سوال: وارون تابع را بدست آورید.
جواب:
به چه توابعی یک به یک می گوییم؟
اگر یک تابع باشد و به هر عنصر در برد دقیقا یک عنصر از دامنه نظیر شود تابع وارون پذیر است. اگر تابعی چنین ویژگی داشته باشد آن را یک به یک نامیم به عبارت دیگر تابع
یک به یک است هرگاه هر دو عنصر متمایز در دامنه به دو عنصر متمایز در برد نظیر شوند.
نکته: اگر تابعی یک به یک باشد آنگاه وارون پذیر است. وارون هر تابع یک به یک، خود یک تابع است.
نکته: به طور کلی می توان گفت که در نمایش مختصاتی یک تابع، تابع در صورتی یک به یک است که هر خط موازی محور ها، نمودار آن را حداکثر در یک نقطه قطع کند.
نکته: در نمایش پیکانی یک تابع زمانی یک به یک است که به هیچ عنصری از هم دامنه بیشتر از یک پیکان وارد نشود.
نکته: در نمایش زوج مرتبی یک تابع ، زمانی تابع یک به یک است که در هیچ دو زوج مرتب متمایزی مولفه دوم یکسان نباشد.
نکته : در نمایش ضابطه ای تابع باید بررسی شود به ازای هر یک و فقط یک
داشته باشیم.
سوال: آیا رابطه هر شخص با کد ملی اش یک به یک است؟
جواب: بله چون هر شخص فقط یک کد ملی دارد پس رابطه تابع هست و چون هیچ دو نفری کدملی مشترکی ندارند پس تابع یک به یک است.
سوال: بررسی کنید آیا تابع ِ یک به یک هست یا نه؟
جواب: چون مولفه دوم تکراری دارد در حالی که مولفه های اول نظیر برابر نیستند پس تابع یک به یک نیست.
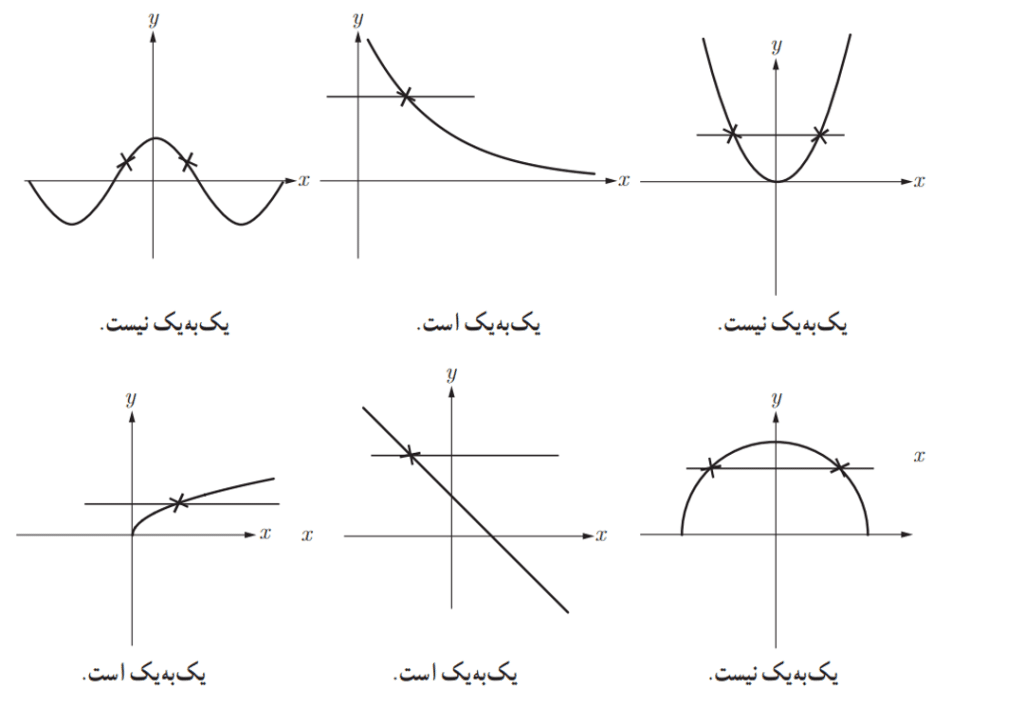
سوال:کدامیک از توابع زیر یک به یک است؟
جواب در کنار هر شکل نوشته شده است:
محدود کردن دامنه برای یک به یک کردن یک تابع غیر یک به یک
اگر تابعی یک به یک نباشد وارون پذیر هم نیست اما گاهی با محدود کردن دامنه یک تابع، می توان تابعی یک به یک بدست آورد. برای محدود کردن دامنه در نوابع درجه دوم به طول سهمی و در توابع قدرمطلقی به ریشه قدرمطلق توجه کنید.
نکته: هر تابع درجه دو تابع یک به یک نیست اما با محدود کردن دامنه می توان آن را یک به یک کرد به این ترتیب که بازه ای که انتخاب می کنیم در یک طرف راس سهمی باشد. یعنی بزرگترین بازه ای که سهمی در آن یک به یک است
یا
می باشد.
سوال: آیا تابع وارون تابع
است؟
جواب: خیر تابع ثابت است و اصلا یک به یک نیست پس وارون پذیر هم نیست پس وارونش نمی تواند یک تابع باشد.
سوال: با محدود کردن دامنه تابع یک تابع یک به یک بدست آورده و دامنه و برد
و وارون آن را بنویسید و این دو تابع را رسم کنید.
جواب:
چطور وارون یک تابع را بدست آوریم؟
*برای بدست آوردن ضابطه تابع وارون یک تابع یک به یک مانند در معادله
در صورت امکان
را برحسب
محاسبه می کنیم سپس با تبدیل
به
،
را بدست می آوریم.
- *در نمایش زوج مرتبی کافیست جای مولفه اول را با مولفه دوم در هر زوج مرتب عوض کنیم.
- *در نمایش پیکانی کافیست جای دو دایره ی دامنه و برد را عوض کنیم.
توجه: ترکیب هر تابع با وارونش برابر با می شود یعنی:
در نتیجه اگر دو تابع و
به گونه ای باشند که:
آنگاه توابع و
وارون یکدیگرند.
تذکر: جای دامنه و برد دو تابع وارون با هم عوض می شود. یعنی دامنه تابع با برد وارونش برابر است و برد تابع با دامنه وارونش برابر است.
نکته: وارون ترکیب دو تابع برابر است با
سوال: تابع با ضابطه را در نظر بگیرید. آیا
یک به یک است؟ وارون آن را بدست آورید.
جواب:
بله یک به یک است.
سوال: اگر مقادیر
و
و
را بدست آورید.
جواب:
جمع بندی
در این مقاله به بیان تعریف وارون تابع و تابع یک به یک پرداخته شده است همچنین بیان شده که چطور با محدود کردن یک تابع وارون ناپذیر آن را تبدیل به یک تابع یک به یک کنیم. در ضمن چندین سوال از موضوعات بحث شده در مقاله حل شده است تا بهتر متوجه اهمیت موضوع در حل مسائل ریاضی شوید. لطفا یک تابع وارون ناپذیر که در زندگی روز مره خود با آن مواجه هستید در قسمت کامنت ها بنویسید. امیدواریم از این مقاله بهره لازم را برده باشید. اگر تمایل دارید که به صورت جامع و بهمراه نمونه سوالات کنکور و نهایی در سالهای مختلف این مطالب را بیاموزید دوره جبر معادله تابع فرامث را تهیه کنید. لطفا ما را از نظرات خود درباره مقاله وارون توابع یک به یک بهره مند کنید.

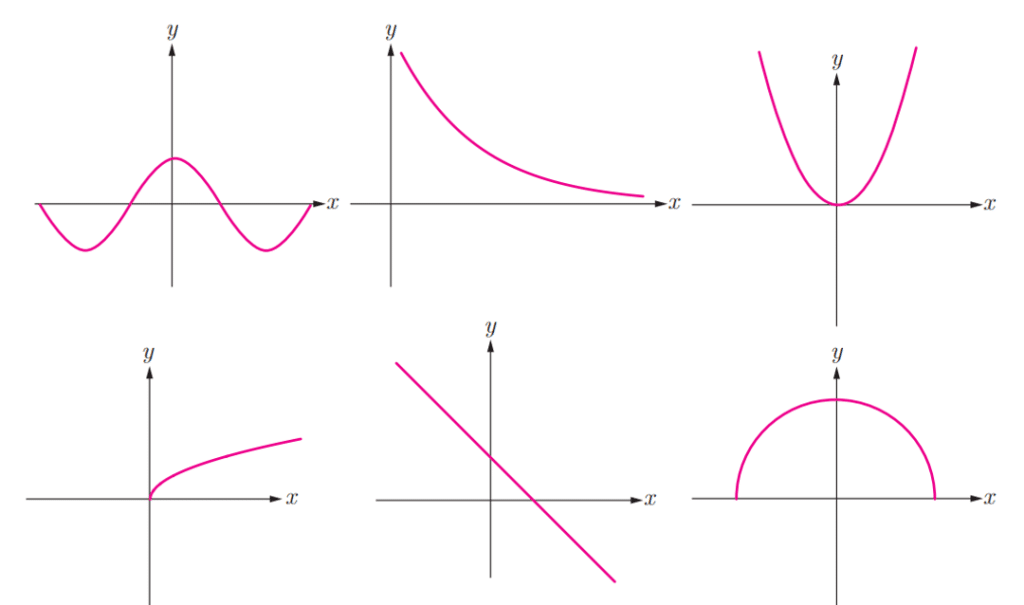
![Rendered by QuickLaTeX.com \[\rightarrow \, \begin{cases} f(x)=(x-2)^{2}+1 & x \ge 2 \\ f(x)=(x-2)^{2}+1 & x \le 2 \end{cases}\]](https://faramath.com/core/ql-cache/quicklatex.com-c6620d75a98782f1de67c1e7f3eabd38_l3.png)
![Rendered by QuickLaTeX.com \[\rightarrow \,\begin{cases} y=(x-2)^{2}+1 & x \ge 2 \\ y=(x-2)^{2}+1 & x \le 2 \end{cases}\]](https://faramath.com/core/ql-cache/quicklatex.com-b66d36af4f67bce639105f04f44e7c90_l3.png)
![Rendered by QuickLaTeX.com \[\rightarrow \, \begin{cases} y-1=(x-2)^{2} & x \ge 2 \\ y-1=(x-2)^{2} & x \le 2 \end{cases}\]](https://faramath.com/core/ql-cache/quicklatex.com-63b7e6c106d653eda6eb8d48a1ece419_l3.png)
![Rendered by QuickLaTeX.com \[\rightarrow \, \begin{cases} x-2=+\sqrt{y-1} & x \ge 2 \\ x-2=-\sqrt{y-1} & x \le 2 \end{cases}\]](https://faramath.com/core/ql-cache/quicklatex.com-c8048d42785d01fbf4d29cc5522f50f8_l3.png)
![Rendered by QuickLaTeX.com \[\rightarrow \, \begin{cases} x=+\sqrt{y-1}+2 & x \ge 2 \\ x=-\sqrt{y-1}+2 & x \le 2 \end{cases}\]](https://faramath.com/core/ql-cache/quicklatex.com-e2ead5e5f4f2979538f8851bb1516335_l3.png)
![Rendered by QuickLaTeX.com \[\rightarrow \, \begin{cases} f^{-1}(x)=+\sqrt{x-1} & y \ge 2 \\ f^{-1}(x)=-\sqrt{x-1} & y \le 2 \end{cases}\]](https://faramath.com/core/ql-cache/quicklatex.com-71db3a6396c601587d2345e6f60cc2e5_l3.png)
![Rendered by QuickLaTeX.com \[\rightarrow \, \begin{cases} D_{f^{-1}}=[1,+\infty) & R_{f^{-1}}=[2,+\infty) \\ D_{f^{-1}}=[1,+\infty) & R_{f^{-1}}=(-\infty, 2] \end{cases}\]](https://faramath.com/core/ql-cache/quicklatex.com-95e5f023ab3b21c922712452b70d7ca1_l3.png)

2 پاسخ
اخ جووووون بالاخره وارون و یک به یک رو یاد گرفتم
مررررسسسسسییییییییی
برات خوشحالم عزیزم . موفق باشی