آموزشی جامع درباره ی انواع خط، معادله خط، رسم خط و حالت های دو خط نسبت به هم
معادله خط روشی برای نشان دادن و معرفی یک خط به صورت منحصربفرد است. معادله یک خط از روی مختصات دو نقطه دلخواه روی آن خط بدست می آید همچنین با کمک دو نقطه روی خط می توان آن را رسم کرد. دلیل آنکه داشتن دو نقطه از خط برای معرفی آن مهم است این است که طبق آنچه در مقاله هندسه تحلیلی خواندیم از هر دو نقطه یک خط منحصربفرد می گذرد. در این مقاله به آموزش شناسایی معادله خط، نوشتن معادله یک خط، رسم یک خط با توجه به معادله آن می پردازیم. در نهایت مقاله را با آموزش حل دستگاه شامل دو معادله خط به پایان می بریم.
یک خط چه شکل هایی می تواند داشته باشد؟ عمودی، افقی و مورب
در این بخش به ارائه چند حالت خاص از خط می پردازیم. خط گذرنده از مبدا، خط افقی و خط عمودی در بخش بعد به طور مفصل تری درباره ی خطوط مورب بحث می شود.
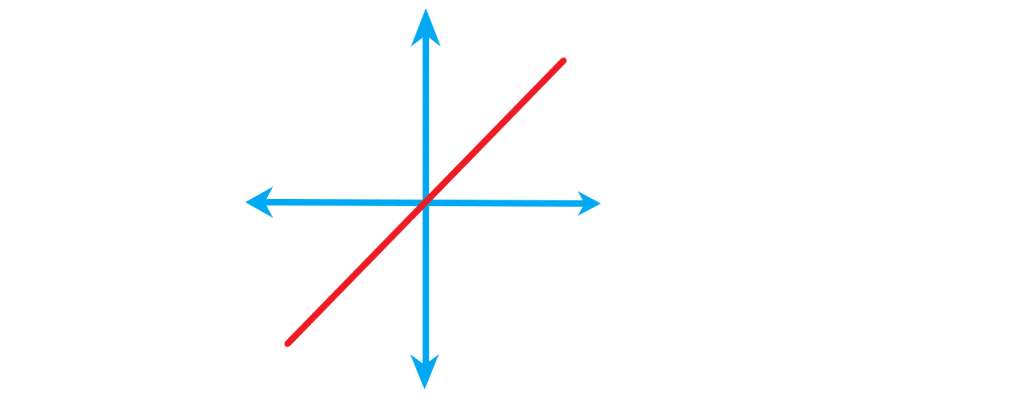
اگر معادله خط به صورت باشد. این خط حتما از مبدا مختصات عبور می کند. در شکل زیر یک نمونه از این خط را می بینید:
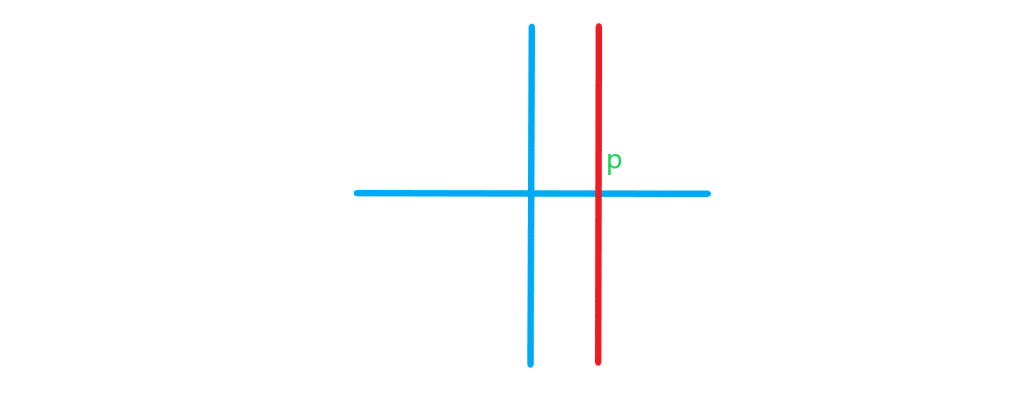
اگر خط به صورت باشد یک خط عمود بر محور طول یا همان موازی با محور عرض را نشان می دهد. این خط شیب بینهایت دارد. همه ی نقاط این خط طول های برابر دارند. در شکل زیر یکی از نمونه های خط عمودی را می بینید:
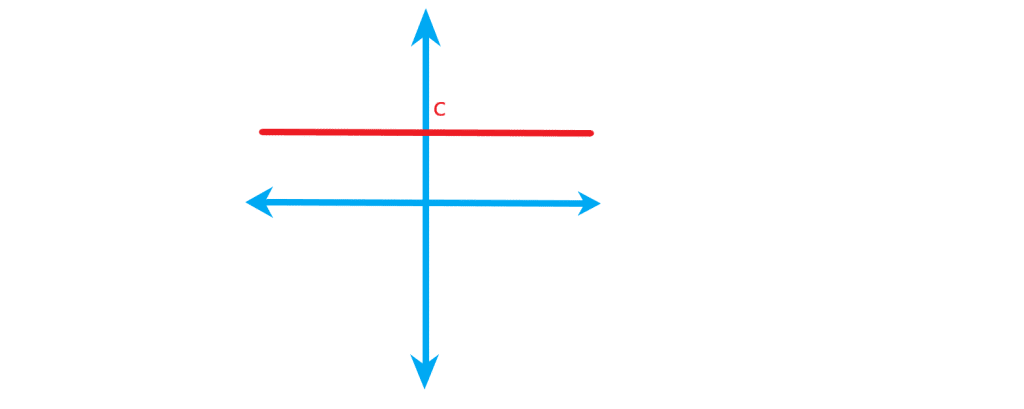
اگر خط به صورت باشد یک خط عمود بر محور عرض یا همان موازی با محور طول را نشان می دهد. این خط شیب صفر دارد. همه ی نقاط این خط عرض های برابر دارند. در شکل زیر یک نمونه از خطوط افقی را می بینید. در بخش انواع توابع می خوانیم که به این دسته از خطوط تابع ثابت می گویند.
چطور معادله یک خط مورب را بنویسیم؟
یک دسته دیگر از خطوط در صفحه وجود دارند که نه افقی اند و نه عمودی به این دسته از خطوط خطوط مورب گویند.
از بخش معادله می دانیم به یک معادله درجه یک می گویند اگر عبارت
الزاما برابر با صفر نباشد و بتواند مقادیر دلخواهی مانند
را بپذیرد، به عبارت
معادله خط می گوییم. چرا که اگر این عبارت را در حالی که
و
دو عدد ثابت حقیقی هستند و
است، به ازای مقادیر مختلفِ
و
که جواب های معادله
هستند در صفحه مختصات رسم کنیم این عبارت یک خط راست را نشان می دهد. در نتیجه می گوییم
و
با هم رابطه خطی دارند. این خط راست همان خط مورب هست.
تذکر: عبارت یک اتحاد نیست چون به ازای هر
و
درست نیست. به این عبارت “معادله خط” می گوییم.
نکته: در معادله خط به
شیب خط می گویند که می تواند زاویه ای که خط با محور طول بسازد را نشان دهد که در بخش مثلثات به آن می پردازیم. و به
عرض از مبدا می گویند که محل برخورد خط به محور عرض ها را نشان می دهد.
برای این دسته از خطوط یعنی خطوط مورب می توانیم معادله خط یا همان ضابطه تابع خطی بنویسیم.برای اینکار باید توجه کنیم که از هر دو نقطه یک خط منحصربفرد می گذرد بنابراین برای اینکه معادله یک خط را داشته باشیم حتما به ما دو نقطه که از آن ها خط موردنظر می گذرد را می دهند و از ما می خواهند که معادله آن خط را بنویسیم. برای این کار باید مراحل زیر را انجام دهیم:
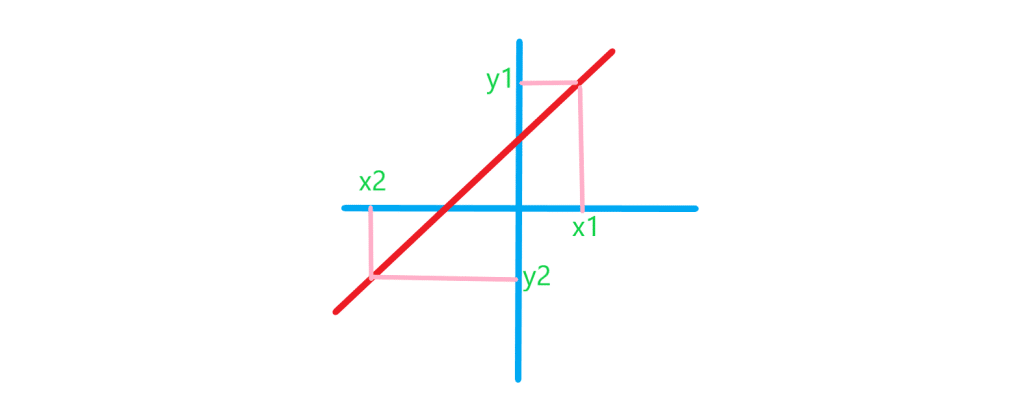
مرحله اول: شیب خط را بدست آورید! برای اینکه شیب خط گذرا از دو نقطه بدست آوریم کافی است از رابطه ی زیر استفاده کنیم:
مرحله دوم: از فرمول زیر برای بدست آوردن معادله خط استفاده کنید:
یا می توان از فرمول زیر استفاده کرد:
که را از جایگذاری یکی از نقاط
یا
در فرمول بالا بدست می آوریم.
چطور یک خط را با توجه به معادله آن رسم کنیم؟
حالا که می دانیم چطور از روی داشتن دو نقطه از یک خط معادله آن را پیدا کنیم می رویم سراغ اینکه پاسخ این سوال را بدهیم که در حالت برعکس چه اتفاقی می افتد. یعنی اگر یک معادله خط را دادند ما چطور آن خط را رسم کنیم. برای این کار دو مقدار دلخواه برای در نظر می گیریم بعد
نظیر هر کدام را بدست می آوریم در نتیجه مختصات دو نقطه که در خط مورد نظر صدق می کنند یعنی
و
را بعنوان دو نقطه روی خط مورد نظر پیدا می کنیم. حالا با پیدا کردن این دو نقطه در صفحه مختصات و وصل کردن این دو نقطه به هم و امتداد آنها از دو طرف خط مورد نظر رسم می شود.
چه موقع دو خط موازی یا عمود یا منطبق اند؟
در حالت کلی می توان معادله خط را به صورت
نوشت.
برای اینکه دو خط بر هم منطبق باشند یا با هم موازی باشند یا بر هم عمود باشند می توان شروط زیر را در نظر گرفت:
*دو خط و
بر هم منطبق اند اگر و فقط اگر ( اگر مفهوم عبارت “اگر و فقط اگر ” برای تان ناآشناست می توانید به مقاله گزاره مراجعه فرمائید) شرط زیر برقرار باشد:
* دو خط و
با هم موازی اند اگر و فقط اگر شرط زیر برقرار باشد:
* دو خط و
بر هم عمودند اگر و فقط اگر شرط زیر برقرار باشد:
اگر معادله دو خط به صورت و
باشد شروط به صورت زیر تغییر می کنند:
*دو خط و
بر هم منطبق اند اگر و فقط اگر شرط زیر برقرار باشد:
* دو خط و
با هم موازی اند اگر و فقط اگر شرط زیر برقرار باشد:
* دو خط و
بر هم عمودند اگر و فقط اگر شرط زیر برقرار باشد:
توجه: اگر تمام ضریب های عددی یک معادله خط را در یک عدد ضرب کنیم خط جدید دقیقا منطبق بر خط قبلی است.
چطور دستگاه با دو معادله خط و دو مجهول را حل کنیم؟
یکی از راه های حل کردن دستگاه های معادله های خطی، حذف کردن یا
است تا به یک معادله یک مجهولی برسیم؛ نام این روش، حذفی است.
برای حل دستگاه دو مجهولی 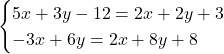
حالا باید معادلات را ساده کنیم:
در مرحله بعد باید کاری کنیم که یکی از متغیر ها یعنی یا
از هر دو معادله حذف شود برای اینکار یکی از معادله ها یا هر دو را در عددی ضرب می کنیم که مجموع ضرایب یکی از متغیرها برابر با صفر شود. مثلا در این دستگاه معادله بالایی را در عدد
ضرب می کنیم تا متغیر
حذف شود:
در ادامه باید دو معادله را با هم جمع کنیم در نتیجه داریم:
در نتیجه جواب هر دو متغیر بدست آمد. .
راه دوم روش جایگزینی است . در این روش برای حل دستگاه 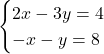
در معادله می توانیم بنویسیم
پس در معادله اول قرار می دهیم
راه سوم روش رسم خطوط هست که هر دو خط را رسم می کنیم و محل برخورد همان جواب هست. فقط در صورتی که خود سوال گفته از این راه دستگاه را حل کنید از این روش استفاده کنید در غیر اینصورت چون ممکن است اشتباه کنید و محل برخورد را درست تشخیص ندهید این روش برای حل دستگاه پیشنهاد نمی شود.
جمع بندی
در این مقاله به آموزش نوشتن معادله خط و رسم یک خط از روی معادله آن پرداختیم. همچنین نشان دادیم که معادلات خطوط عمود بر هم، موازی و منطبق چه رابطه ای با هم دارند. همچنین آموزش دادیم که معادله خط های خاص افقی، عمودی و خط عبوری از مبدا به طور کلی چه شکلی دارند. در نهایت با آموزش دادن حل دستگاه دو مجهولی درجه اول این مقاله را پایان دادیم. اگر علاقمند به یادگیری حل معادله، حل نامعادله و تعیین علامت و حل معادله درجه دوم هستید به مقاله هر کدام مراجعه کنید. اگر تمایل دارید که به صورت جامع و بهمراه نمونه سوالات کنکور و نهایی در سالهای مختلف این مطالب را بیاموزید دوره جبر معادله تابع فرامث را تهیه کنید. لطفا ما را از نظرات خود را در مورد مقاله معادله خط در قسمت کامنت ها بهره مند کنید.

![Rendered by QuickLaTeX.com \[\begin{cases} 5x+3y-2x-2y=+12+3 \\ -3x+6y-2x-8y=8 \end{cases}\]](https://faramath.com/core/ql-cache/quicklatex.com-60402dbfb6ce6e661b623a2998747c81_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} 3x+y=15 \\ -5x-2y=8 \end{cases}\]](https://faramath.com/core/ql-cache/quicklatex.com-9bef543339824ed1ffa226f2ce7c229a_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} 6x+2y=30 \\ -5x-2y=8 \end{cases}\]](https://faramath.com/core/ql-cache/quicklatex.com-19b98d876c2e4ffd8c73926d7bfba44c_l3.png)
