نکات جامع پیرامون برابری دو تابع، اعمال جبری توابع و ترکیب دو تابع
اعمال جبری توابع شامل جمع تفریق ضرب و تقسیم می شود. در این مقاله شرط برابری دو تابع را می آموزیم همچنین یاد می گیریم چه زمان اجازه داریم اعمال جبری بین دو تابع انجام دهیم دامنه های دو تابع باید چه وضعیتی داشته باشند که بتوان اعمال جبری روی دو تابع انجام داد و چطور این عمل باید انجام شود روی اعضای دامنه یا روی اعضای برد؟ برای دانستن جواب این سوالات حتما این مقاله کوتاه اما جامع را از دست ندهید. علاوه بر اعمال جبری روی توابع می توانید ترکیب توابع را هم در این مقاله بخوانید چه موقع می توان دو تابع را ترکیب کرد. ترکیب دو تابع چه تفاوتی با اعمال جبری توابع دارد؟ ترکیب دو تابع چطور انجام می شود؟ آیا می توان هر دو تابعی را با هم ترکیب کرد؟ جواب این سوالات را در این مقاله بخوانید و بدانید!
چه موقع دو تابع با هم برابرند؟
اگر نمودارهای دو تابع در یک دستگاه مختصات داده شده باشند، هنگامی این دو تابع باهم برابرند که نمودارهای آنها کاملا برهم منطبق شوند.
اگر دو تابع به صورت مجموعه زوج های مرتب داده شده باشند، هنگامی باهم برابرند که به عنوان دو مجموعه باهم برابر باشند.
به طور کلی دو تابع و
را برابر نامیم هرگاه:
*دامنه و دامنه
برابر باشند.
*برای هر از این دامنه یکسان داشته باشیم:
سوال: آیا دو تابع با ضابطه و
با هم برابرند چرا؟
جواب: خیر چون دامنه تابع برابر
است اما دامنه تابع
برابر
است در نتیجه دو تابع برابر نیستند.
اعمال جبری توابع: جمع و تفریق و ضرب و تقسیم دو تابع
همانگونه که عمل های ضرب و جمع برای دو عدد یا چند جمله ای امکان پذیر است برای دو تابع هم چنین اعمالی قابل انجام است.
اگر و
دو تابع باشند،
تابعی است که دامنه ی آن مجموعه ی
است و به صورت زیر تعریف می شود:
به طور کلی اگر اگر و
دو تابع باشند توابع
و
و
و
به صورت زیر تعریف می شوند:
توجه: اعمال جبری روی دو تابع برای اعضای مشترکِ دامنه ی دو تابع انجام می شود ولی خود عمل برای اعضای برد انجام می شود.
سوال: اگر و
تابع زوج مرتبی
را بنویسید.
جواب:
ابتدا باید دامنه هر یک از توابع را بدست آوریم:
سپس اشتراک دامنه ها را بدست می آوریم:
پس تابع به صورت زیر مشخص می شود:
می بینیم در این سوال ابتدا اعضای مشترک دامنه ها مشخص شد سپس برد مربوط به هر عضو در دو تابع را با هم جمع کردیم.
ترکیب توابع: چگونه می توان دو تابع را ترکیب کرد؟
اگر یک تابع را ورودی تابع دیگر در نظر بگیریم در واقع دو تابع را ترکیب کردیم. در اعمال جبری بین دو تابع، دو تابع هویت جداگانه ای دارند و اعضای مشترک دامنه شان را با هم جمع یا تفریق یا ضرب یا تقسیم می کنیم اما در ترکیب دو تابع یکی را به عنوان اعضای دامنه دیگری در نظر می گیریم. در ادامه نحوه ساخت ترکیب دو تابع را با هم می بینیم:
مراحل ساخت تابع : مرحله اول
ورودی و
خروجی است. (
باید در دامنه تابع
باشد) مرحله دوم :
ورودی و
خروجی است. (
باید در دامنه تابع
باشد)
اگر و
دو تابع باشند به طوری که برد تابع
و دامنه تابع
اشتراک ناتهی داشته باشند، تابع
را با نماد
نمایش می دهیم و تابع
را تابع مرکب می نامیم به عبارت دیگر:
دامنه تابع مرکب: دامنه تابع مرکب مجموعه
هایی است که هم زمان در دو شرط زیر صدق کنند:
-
در دامنه
قرار داشته باشد.
در دامنه
قرار داشته باشد.
به طور مشابه دامنه برابر است با
تذکر: دامنه توابع مرکب را همیشه با توجه به تعاریف آن به دست می آوریم نه از روی ضابطه آن .
سوال: اگر و
تابع را در صورت امکان بنویسید.
جواب:
N در اینجا به معنای تعریف نشده است.
نکات کلی این مقاله را می توانید در جدول زیر ببینید:
جمع بندی
در این مقاله به بیان برابر دو تابع، اعمال جبری روی دو تابع و ترکیب دو تابع پرداختیم. متوجه شدیم دامنه ی یک تابع جزیی از هویت تابع است که باید در برابر آن تابع با تابع دیگر حتما دامنه را در نظر گرفت همچنین برای انجام اعمال جبری جمع دو تابع تفریق دو تابع ضرب دو تابع و تقسیم دو تابع نیاز داریم به دامنه دو تابع توجه کنیم . ترکیب توابع اما پیچیده تر است و باید برد تابع ورودی با دامنه تابع خروجی با هم اشتراک داشته باشند در غیر اینصورت نمی توان دو تابع را با هم ترکیب کرد. امیدواریم از خواندن این مقاله بهره کافی را برده باشید. اگر تمایل دارید که به صورت جامع و بهمراه نمونه سوالات کنکور و نهایی در سالهای مختلف این مطالب را بیاموزید دوره جبر معادله تابع فرامث را تهیه کنید. لطفا ما را از نظرات خود درباره مقاله اعمال جبری توابع و ترکیب توابع در قسمت کامنت ها بهره مند کنید.

![Rendered by QuickLaTeX.com \[\begin{cases} (gof)(0)=g(f(0))=g(-1)=4\\ (gof)(5)=g(f(5))=g(2)=0\\ (gof)(3)=g(f(3))=g(5)=-7\\ (gof)(-2)=g(f(-2))=g(4)=\text{N } \end{cases}\]](https://faramath.com/core/ql-cache/quicklatex.com-5c0c3e66528c2564e9e4a6cbd7de0cb7_l3.png)
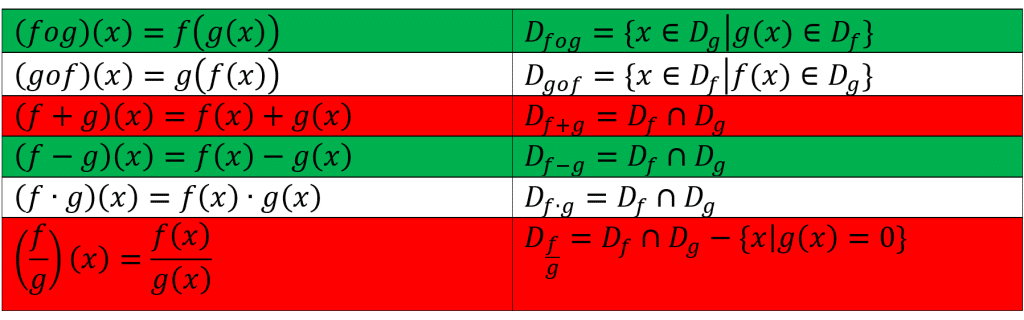

2 پاسخ
وای که چه خوب توضیح می دید می خوام همه ی مقاله ها تون رو بخونم
تو تابستون یه بار دیگه هم می خونم برای سال بعد آماده بشم آخه کنکور دارم …
خوشحالم راضی بودی امیدوارم موفق باشی و نتیجه عالی ای از کنکورت بگیری