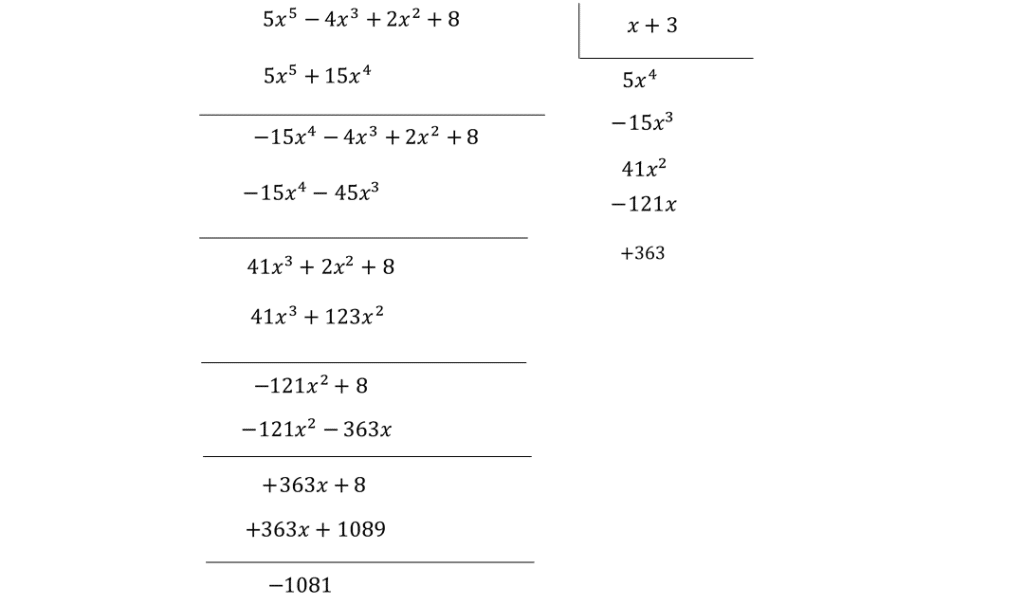جامع ترین آموزش درباب عبارتها وتوابع گویا، معادلات گویا و تقسیم چندجمله ای ها

عبارت گویا نسبت دو چندجمله ای با یکدیگر است و معادله گویا نشان دهنده ی برابری دو عبارت گویاست. برای حل معادله گویا باید بفهمیم که به ازای چه مقادیری از متغیر تساوی برقرار است. در این مقاله به تعریف عبارت گویا می پردازیم و اینکه به ازای چه مقادیری بامعنا هستند. همچنین به آموزش حل معادلات گویا می پردازیم. در میانه ی راه به تقسیم صورت عبارت گویا بر مخرج عبارت گویا که به تقسیم چندجمله ای ها معروف است می پردازیم. در قدم آخر توابع گویا و دامنه ی آنها را تعریف می کنیم. اگر به دنبال آموزشی هستید که هر آنچه که لازم است راجع به عبارت گویا، تقسیم چندجمله ای ها، معادلات گویا و توابع گویا بدانید را به شما آموزش دهد این مقاله بهترین انتخاب است.

به چه عبارت یا تابعی عبارت یا تابع گویا می گویند؟

به طور کلی هر عبارت گویا، کسری است که صورت و مخرج آن چندجمله ای باشد. عبارات گویا به طور کلی به صورت $\frac{P(x)}{Q(x)}$ هستند، که در آن $P(x)$ و $Q(x)$ چندجمله ای هستند و چندجمله ای $Q(x)$ صفر نیست. در واقع برای تعیین همه مقادیری که به ازای آنها یک عبارت گویا تعریف می شود، باید مقادیری از متغیر را حذف کنیم که به ازای آنها مخرج کسر صفر می شود ؛ به عبارت دیگر این مقادیر را نمی توان به جای متغیر در عبارت جبری قرار داد و حاصل را محاسبه کرد.

درواقع هر تابع به شکل $f(x)=\frac{P(x)}{Q(x)}$ را یک تابع گویا می نامیم که در آن $P(x)$ و $Q(x)$ چند جمله ای هستند و چند جمله ای $Q(x)$ صفر نیست.

دامنه یک تابع گویا مجموعه ی همه ی اعدادی است که مخرج آن را صفر نمی کند.

مثال: عبارت های $\frac{9x^{2}+3x-\sqrt[3]{10}}{5x+7}$ و $\frac{9x^{2}+3x-10}{5x^{3}+\sqrt{7}x^{2}-13x+12}$ گویا هستند. اما عبارت $\frac{9x^{2}+3x-10}{5x+7+\sqrt{x}}$ یک عبارت گویا نیست چون مخرج آن چند جمله ای نیست. (در مخرج متغیر زیر رادیکال رفته است)

توجه : وقتی می گوییم یک عبارت چند جمله ای است فقط کافی است متغیر های آن عبارت توان های طبیعی داشته باشند و ضرایب و اعداد ثابت می توانند هر عدد حقیقی ای باشند.

نکته : وقتی حاصل ضرب چند عبارت برابر صفر شود، حداقل یکی از آنها صفر است.

مثلا در $(x+5)(x-7)=0$ می توان گفت که $(x+5)=0$ یا $(x-7)=0$ بنابراین می توان گفت $x=-5$ یا $x=7$ یعنی عبارت $(x+5)(x-7)$ به ازای $x=-5$ یا $x=7$ برابر با صفر می شود.

چطور عبارت های گویا را با هم جمع یا تفریق کنیم؟

جمع و تفریق عبارت های گویا مشابه جمع و تفریق اعداد گویا است. ابتدا باید مخرج مشترک گرفت و بعد از مخرج مشترک گرفتن، صورت کسرها را با هم جمع یا تفریق کرد.

در ادامه چند مثال را با هم حل می کنیم:

$\frac{3x+5}{-2x+7}+\frac{x+4}{-2x-7}$

$=\frac{(3x+5)(-2x-7)}{(-2x+7)(-2x-7)}+\frac{(x+4)(-2x+7)}{(-2x-7)(-2x+7)}$

$=\frac{-6x^{2}-21x-10x-35}{4x^{2}-49}+\frac{-2x^{2}+7x-8x+28}{4x^{2}-49}$

$=\frac{-8x^{2}-32x-7}{4x^{2}-49}$

برای حل این سوال ابتدا مخرج مشترک می گیریم سپس با توجه به علامت جمع یا تفریق صورت کسرهای جدید را با هم جمع و تفریق می کنیم.

$\frac{3x+5}{-2x+7}-\frac{x+4}{-2x-7}$

$=\frac{(3x+5)(-2x-7)}{(-2x+7)(-2x-7)}-\frac{(x+4)(-2x+7)}{(-2x-7)(-2x+7)}$

$=\frac{-6x^{2}-21x-10x-35}{4x^{2}-49}-\frac{-2x^{2}+7x-8x+28}{4x^{2}-49}$

$=\frac{-6x^{2}-21x-10x-35}{4x^{2}-49}+\frac{2x^{2}-7x+8x-28}{4x^{2}-49}$

$=\frac{-4x^{2}-28x-63}{4x^{2}-49}$

توجه کنید که علامت منفی پشت کسر را در همه ی جملات موجود در صورت کسر تاثیر می دهیم.

چطور عبارت های گویا را با هم ضرب و تقسیم کنیم؟

ضرب و تقسیم عبارت های گویا شبیه ضرب و تقسیم اعداد گویا است. عبارت های گویا را با کمک اتحاد ها و فاکتور گرفتن می توان به صورت حاصل ضرب نوشت و در نهایت ساده کرد.

در ادامه چند مثال را با هم میبینیم:

$\frac{-2x+7}{5x-9}\times \frac{x+8}{7x-1}$

$=\frac{(-2x+7)(x+8)}{(5x-9)(7x-1)}$

$=\frac{-2x^{2}-16x+7x+56}{35x^{2}-5x-63x+9}$

$=\frac{-2x^{2}-9x+56}{35x^{2}-68x+9}$

در این مثال می بینیم دو عبارت گویا در هم ضرب شده اند در این حالت باید صورت کسرها را در هم ضرب کنیم و مخرج کسرها را در هم ضرب کنیم.

$\frac{3x-1}{x+5}\div \frac{-6x+2}{2x+20}$

$=\frac{3x-1}{x+5} \times \frac{2x+20}{-6x+2}$

$=\frac{(3x-1)(2)(x+10)}{(x+5)(-2)(3x-1)}$

$=\frac{x+10}{-x-5}$

در این مثال می بینیم دو عبارت گویا را تقسیم می کنیم. مانند آنچه در تقسیم اعداد گویا آموختیم، باید عبارت گویای اول را بنویسیم سپس آن را در معکوس عبارت دوم ضرب کنیم. در این عبارت می بینیم که $(3x-1)$ و $(2)$ هم در صورت و هم در مخرج وجود دارد پس از هر دو صورت و مخرج کسر ساده می شود.

چطور کسرهای مرکب را ساده کنیم؟

هنگام ساده کردن هر عبارت گویای مرکب، همانند کسرهای مرکب می توان صورت و مخرج را جداگانه ساده و سپس آنها را برهم تقسیم کرد و یا از همان ابتدا صورت و مخرج را در عبارتی مناسب و غیرصفر ضرب کرد. ( صورت و مخرج کسر خودش شامل جمع و تفریق عبارات گویا است)

$\frac{ n-\frac{n^{2}}{n-m}}{1+\frac{m^{2}}{n^{2}-m^{2}}}$

$=\frac{\frac{n^{2}-nm}{n-m}-\frac{n^{2}}{n-m}}{\frac{n^{2}-m^{2}}{n^{2}-m^{2}}+\frac{m^{2}}{n^{2}-m^{2}}}$

$=\frac{\frac{-nm}{n-m}}{\frac{n^{2} }{ n^{2}-m^{2}}}$

$\frac{-nm\times (n^{2}-m^{2})}{n^{2}(n-m)}$

$=\frac{-nm\times(n-m)(n+m)}{ n^{2}(n-m)}$

$=\frac{-m(n+m)}{n}$

$\frac{\frac{y}{x+y}-\frac{x}{x-y}}{\frac{x}{x+y}+\frac{y}{x-y}}$

$=\frac{\frac{xy-y^{2}-x^{2}-xy}{x^{2}-y^{2}}}{\frac{x^{2}-xy+xy+y^{2}}{x^{2}-y^{2}}}$

$=\frac{(xy-y^{2}-x^{2}-xy)(x^{2}-y^{2})}{(x^{2}-xy+xy+y^{2})(x^{2}-y^{2})}$

$\frac{(-y^{2}-x^{2})(x^{2}-y^{2})}{(x^{2}+y^{2})(x^{2}-y^{2})}$

$=\frac{-(y^{2}+x^{2})(x^{2}-y^{2})}{(x^{2}+y^{2})(x^{2}-y^{2})}=-1$

چطور مخرج یک کسر را گویا کنیم؟

برای گویا کردن مخرج کسرهایی که شامل یک عبارت رادیکالی هستند، می توانیم آن کسر را دریک عبارت رادیکالی مناسب، ضرب و تقسیم کنیم تا مخرج کسر گویا شود. مثلا برای گویا کردن کسر $\frac{2}{\sqrt{3}}$ کافی است صورت و مخرج کسر را در $\sqrt{3}$ ضرب کنیم. اما در مورد $\frac{2}{\sqrt{3}-\sqrt{5}}$ باید چه کنیم؟ برای گویا کردت این کسر باید از اتحاد ها کمک بگیریم. کدام اتحاد؟ کدام اتحاد است که دو مولفه دارد و هر دو را به توان دوم می رساند؟ آفرین اتحاد مزدوج. در اتحاد مزدوج تساوی $(a+b)(a-b)=a^{2}-b^{2}$ برقرار است در سوال ما $a=\sqrt{3}$ و $b=\sqrt{5}$ در نتیجه می توان نوشت:

$(\sqrt{3}-\sqrt{5})(\sqrt{3}+\sqrt{5})=(\sqrt{3})^{2}-(\sqrt{5})^{2}=3-5=-2$

حالا که متوجه شدیم مخرج کسر ضربدر چه عبارت رادیکالی ای تبدیل به عدد صحیح می شود می توانیم بنویسیم:

$\frac{2}{\sqrt{3}-\sqrt{5}}$

$=\frac{2}{\sqrt{3}-\sqrt{5}}\times \frac{(\sqrt{3}+\sqrt{5}}{(\sqrt{3}+\sqrt{5})}$

$=\frac{2\sqrt{3}+2\sqrt{5}}{-2}$

$=-\sqrt{3}-\sqrt{5}$

چطور چندجمله ای ها را بر هم تقسیم کنیم؟ بخش پذیری چه زمانی اتفاق می افتد؟

تقسیم چند جمله ای ها را در سه قسمت بیان کردیم تقسیم یک جمله ای بر یک جمله ای، تقسیم چندجمله ای بر یک جمله ای و تقسیم چندجمله ای برچند جمله ای. در ادامه هر قسمت را می توانید ببینید.

تقسیم تک جمله ای بر تک جمله ای

برای تقسیم دو تک جمله ای بر یکدیگر از قوانین ساده کردن کسرها و نیز قوانین مربوط به ساده کردن توانها استفاده می کنیم.

مثلا برای تقسیم تک جمله ای $5x^{2}$ بر تک جمله ای $10xy$ ابتدا به این توجه می کنیم که هر کدام حاصل ضرب چه متغیر یا عددی هستند. سپس اعداد و متغیرهای مشترکِ صورت و مخرج را با هم ساده می کنیم:

$\frac{5x^{2}}{10xy}$

$=\frac{5\times x \times x}{2\times 5\times x \times y}$

$=\frac{x}{2y}$

تقسیم چند جمله ای بر تک جمله ای

در این حالت هر جمله صورت را جداگانه بر مخرج تقسیم می کنیم و در نهایت حاصل را با هم جمع می کنیم.

مثلا برای تقسیم چند جمله ای $5x^{2}+10y^{3}-30xy$ بر تک جمله ای $10xy$ هر جمله از چندجمله ای $5x^{2}+10y^{3}-30xy$ را جداگانه بر تک جمله ای $10xy$ با توجه به قانون تقسیم یک جمله ای بر یک جمله ای تقسیم می کنیم.

$\frac{5x^{2}+10y^{3}-30xy}{10xy}$

$=\frac{5x^{2}}{10xy}+\frac{10y^{3}}{10xy}+\frac{-30xy}{10xy}$

$=\frac{x}{2y}+\frac{y^{2}}{x}+(-3)$

تقسیم چند جمله ای بر چند جمله ای

در این حالت صورت و مخرج را به ترتیب درجه مرتب می کنیم و تقسیم را انجام می دهیم باقی مانده حتما درجه ای کمتر از مخرج (یا مقسوم علیه) دارد.

اگر باقی مانده صفر باشد می گوییم مقسوم بر مقسوم علیه بخش پذیر است.

مثلا برای تقسیم چندجمله ای $8-4x^{3}+5x^{5}+2x^{2}$ بر چندجمله ای $x+3$ ابتدا درجه هر کدام را به ترتیب از بزرگتر به کوچکتر مرتب می کنیم. چندجمله ای $8-4x^{3}+5x^{5}+2x^{2}$ به صورت چندجمله ای $5x^{5}-4x^{3}+2x^{2}+8$ نوشته می شود. چند جمله ای $x+3$ که مرتب است. حالا می توانیم تقسیم را انجام دهیم.

همانطور که در تقسیم بالا می بینیم ابتدا بزرگترین درجه مقسیم را بر بزرگترین درجه مقسوم علیه تقسیم می کنیم یعنی $5x^{5}$ را بر $x$ تقسیم می کنیم که حاصل برابر با $5x^{4}$ می شود. حالا حاصلضرب $x+3$ در $5x^{4}$ را بدست می آوریم که برابر با $5x^{5}+15x^{4}$ می شود حالا حاصل تفریق مقسوم و این مقدار را بدست می آوریم. در این مرحله فرآیند تقسیم تکرار می شود و این کار را آنقدر ادامه می دهیم که درجه باقی مانده تفریق از درجه مقسوم علیه کوچکتر باشد. از آنجا که درجه $-15x^{4}-4x^{3}+2x^{2}+8$ برابر 4 است و درجه $x+3$ برابر یک بنابراین باید تقسیم را ادامه دهیم. حالا باید $-15x^{4}$ را بر $x$ تقسیم کنیم. حاصل برابر با $-15x^{3}$ می شود حالا $-15x^{3}$ را در $x+3$ ضرب می کنیم. و حاصل ضرب را از عبارت $-15x^{4}-4x^{3}+2x^{2}+8$ کم می کنیم. حاصل برابر $41x^{3}+2x^{2}+8$ می شود که باز هم درجه بزرگتری از مقسوم علیه دارد بنابراین باید تقسیم را ادامه دهیم. حالا $41x^{3}$ را بر $x$ تقسیم می کنیم حاصل برابر $41x^{2}$ می شود این عبارت یک جمله ای را در مقسوم علیه ضرب می کنیم و عمل تفریق را انجام می دهیم حاصل تفریق $-121x^{2}+8$ می شود حالا جمله با بزرگترین درجه یعنی $-121x^{2}$ را بر $x$ که بزرگترین درجه مقسوم علیه را دارد تقسیم می کنیم که برابر با $-121x$ می شود این عبارت را در مقسوم علیه ضرب می کنیم و حاصل را از $-121x^{2}+8$ کم می کنیم که حاصل تفریق $+363x+8$ می شود که درجه آن با مقسوم علیه برابر است بنابراین باید تقسیم را ادامه دهیم به همین علت $363x$ را بر $x$ تقسیم می کنیم و حاصل برابر با $363$ می شود. این عدد را در مقسوم علیه ضرب می کنیم و حاصل را از $+363x+8$ کم می کنیم باقیمانده برابر با $-1081$ می شود حالا چون درجه باقیمانده درجه صفر است و از درجه مقسوم علیه کمتر است تقسیم را ادامه نمی دهیم. در واقع تقسیم به طور کامل انجام شده است.

در این تقسیم چندجمله ای $5x^{5}-4x^{3}+2x^{2}+8$ مقسوم و چندجمله ای $x+3$ مقسوم علیه و $-1081$ باقی مانده و $5x^{4}-15x^{3}+41x^{2}-121x-1081$ برابر خارج قسمت این تقسیم است.

تقسیم و بخش پذیری

در عبارت گویای $\frac{f(x)}{p(x)}$ اگر $f(x)$ و $p(x)$ چندجمله ای باشند و درجه $p(x)$ از صفر بزرگتر باشد آنگاه چندجمله ای های منحصربفرد $q(x)$ و $r(x)$ وجود دارند به طوری که $f(x)=p(x)q(x)+r(x)$ که در آن $r(x)=0$ (که یعنی چندجمله ای $f(x)$ بر چندجمله ای $p(x)$ بخش پذیر است) یا $r(x)\neq 0$ و درجه $r(x)$ از درجه $p(x)$ کمتر است.

در عبارت $f(x)=p(x)q(x)+r(x)$ که با توجه به تقسیم $f(x)$ بر $p(x)$ با توجه به عبارت گویای $\frac{f(x)}{p(x)}$ نوشته شده است به $f(x)$ مقسوم، به $p(x)$ مقسوم علیه، به $q(x)$ خارج قسمت و به $r(x)$ باقیمانده می گویند. با توجه به آنچه پیشتر خواندیم همواره درجه باقی مانده از مقسوم علیه کمتر است.

قضیه : باقی مانده تقسیم چندجمله ای $f(x)$ بر $ax+b$ عبارت است از $r(x)=f(\frac{-b}{a})$

مثلا برای اینکه باقیمانده تقسیم چند جمله ای $5x^{5}-4x^{3}+2x^{2}+8$ بر چندجمله ای درجه اول $x+3$ را پیدا کنیم می توانیم به جای تقسیم کردن که در بالاتر توضیح داده شد، از قضیه فوق استفاده کنیم برای اینکار ابتدا باید ریشه معادله درجه اول را محاسبه کنیم. داریم: $x+3=0$ پس $x=-3$ در مرحله بعد باید این مقدار بدست آمده را در چندجمله ای مقسوم قرار دهیم. بنابراین داریم:

$5x^{5}-4x^{3}+2x^{2}+8$

$=5(-3)^{5}-4(-3)^{3}+2(-3)^{2}+8$

$=-1215+108+18+8=-1081$

که می بینیم عدد بدست آمده دقیقا برابر با باقیمانده تقسیمی است که در بالاتر محاسبه شده است.

چطور یک معادله گویا را حل کنیم؟

برای حل یک معادله گویا می توان دو طرف تساوی را پس از تجزیه کردن مخرج ها، در کوچکترین مضرب مشترک مخرج ها ضرب کرد تا معادله از شکل کسری خارج شود. بعد از اینکه با توجه به این روش معادله حاصل را حل کردیم ، جواب های بدست آمده نباید مخرج هیچ یک از کسرها را صفر کند. همچنین ممکن است برخی از جواب ها با شرایط مسئله در محیط پیرامونی مطابقت نداشته باشند که این جواب ها نیز مورد قبول نیستند.

برای حل معادله های شــامل عبارتهــای گویا، ابتدا با توجه بــه خاصیت های معادله و مخــرج مشــترک گیری، معادلــه ای نظیر $\frac{P(x)}{Q(x)}=0$ بدست می آید. به شرط اینکه $Q(x)\neq 0$ ، وقتی معادله جواب دارد که $P(x)=0$ است سپس ریشه های معادله را $P(x)=0$ به دست می آوریم. از بین ریشه های به دســت آمده، آنهایی را قبول می کنیم که مخرج کسر $\frac{P(x)}{Q(x)}$ یعنی $Q(x)$ را صفر نکند.

نکته : اگر در یک مستطیل با طول $L$ و عرض $W$ داشته باشیم

$\frac{L}{W}=\frac{L+W}{L}$

آنگاه به این مستطیل، مستطیل طلایی می گوییم.

مثال اول از حل معادله گویا (صورت و مخرج از درجه اول)

مثلا برای حل معادله گویای $\frac{x+10}{-x-5}=0$ ابتدا باید صورت کسر را برابر با صفر قرار دهیم بنابراین قرار می دهیم

$x+10=0\,\,\,\rightarrow\,\,\,x=-10$

حالا باید $x=-10$ را در مخرج قرار می دهیم تا ببینیم صفر می شود یا نه اگر صفر نشد $x=-10$ را به عنوان جواب قبول می کنیم اما اگر این عدد مخرج را صفر کرد می گوییم معادله گویا جواب ندارد. که می بینیم با قرار دادن $x=-10$ در $-x-5$ حاصل برابر با $-(-10)-5=+10-5=5$ می شود که صفر نیست پس $x=-10$ را به عنوان جواب معادله گویا قبول می کنیم.

مثال دیگری که در ادامه می بینیم نیاز به اطلاعات حل معادله درجه دو دارد. برای داشتن این اطلاعات لطفا به مقاله مربوطه مراجعه کنید.

مثال دوم از حل معادله گویا (صورت و مخرج از درجه دوم)

در مثال بعدی یک معادله گویا به صورت $\frac{x^{2}+7x+10}{x^{2}+9x+14}=0$ ابتدا باید ریشه های صورت را بدست آوریم. برای این کار قرار می دهیم: $x^{2}+7x+10=0$ حالا با استفاده از روش دلتا در معادله درجه دو ریشه های این معادله را بدست می آوریم:

$x^{2}+7x+10=0$

$\rightarrow\,\,\,\Delta=7^{2}-4(1)(10)=9$

$\rightarrow\,\,\,x=-2\,\,,\,\,x=-5$

حالا باید بررسی کنیم که این دو ریشه مخرج را صفر می کنند یا نه. برای این کار دو راه داریم یا می توانیم هر کدام از این ریشه های بدست آمده را درون چند جمله ای مخرج قرار دهیم و راه دیگر اینکه ریشه های مخرج را بدست آوریم و بررسی کنیم کدام ریشه ها ریشه های مخرج هم هستند. در ادامه به بررسی هر دو روش می پردازیم. توجه شود که در هر سوال از روشی که محاسباتش آسان تر است استفاده می کنیم.

روش اول: در این روش هر کدام از اعداد بدست آمده را در عبارت چندجمله ای مخرج قرار می دهیم:

$x^{2}+9x+14$

$=(-2)^{2}+9(-2)+14$

$=4-18+14=0$

با توجه به محاسبه انجام شده در می یابیم که عدد $-2$ ریشه مخرج هم هست بنابراین نمی توان آن را به عنوان ریشه معادله گویا در نظر گرفت.

$x^{2}+9x+14$

$=(-5)^{2}+9(-5)+14$

$=25-45+14=-6$

می بینیم که عدد $-5$ مخرج را صفر نمی کند بنابراین می توان آن را به عنوان ریشه معادله گویا در نظر گرفت. بنابراین می توان گفت معادله گویای $\frac{x^{2}+7x+10}{x^{2}+9x+14}=0$ در مجموعه اعداد حقیقی فقط یک ریشه دارد و آن هم عدد $x=-5$ است.

روش دوم: در این روش، ریشه های عبارت مخرج را بدست می آوریم:

$x^{2}+9x+14=0$

$\rightarrow\,\,\,\Delta=9^{2}-4(1)(14)=25$

$\rightarrow\,\,\,x=-2\,\,x=-7$

می بینیم که یکی از ریشه های صورت یعنی $x=-2$ ریشه مخرج نیز هست بنابراین آن را به عنوان جواب معادله گویا نمی پذیریم. و معادله ی گویا فقط یک ریشه قابل قبول یعنی $x=-5$ دارد.

می بینیم هر دو روش به یک نتیجه مشابه می رسند. هر دو روش قابل اعتماد و کاربردی هستند.

نکته: با توجه به اینکه ریشه های صورت و مخرج را بدست آوردیم می توانیم به جای عبارت گویای $\frac{x^{2}+7x+10}{x^{2}+9x+14}$ بنویسیم $\frac{(x+2)(x+5)}{(x+2)(x+7)}$ حالا می توان عبارت $x+2$ را از صورت و مخرج حذف و ساده کرد. در واقع با دیدگاهی که از حل معادله گویا بدست آوردیم می توانیم در ساده کردن عبارت های گویا نیز استفاده کنیم.

جمع بندی

در این مقاله اطلاعات جامعی از عبارت گویا و نحوه حل معادلات گویا و تقسیم چند جمله ای ها دریافت کردیم. همچنین در این مقاله نحوه ضرب و تقسیم و جمع و تفریق عبارت های گویا را آموختیم. ساده کردن عبارت های مرکب از جمله مطالبی است که در این مطلب آموزش داده شده است. اگر به اطلاعات پایه در مورد اعداد گویا، عبارت های جبری، معادله و دامنه و برد توابع نیاز دارید لطفا به هر کدام از این مقالات مراجعه کنید. امیدواریم از خواندن مقاله عبارت ها و معادلات گویا بهره کافی برده باشید. اگر تمایل دارید که به صورت جامع و بهمراه نمونه سوالات کنکور و نهایی در سالهای مختلف این مطالب را بیاموزید دوره جبر معادله تابع فرامث را تهیه کنید. لطفا ما را از نظرات ارزشمند خود درباره این مقاله بهره مند کنید.

جامع ترین آموزش درباب عبارتها وتوابع گویا، معادلات گویا و تقسیم چندجمله ای ها

به چه عبارت یا تابعی عبارت یا تابع گویا می گویند؟

چطور عبارت های گویا را با هم جمع یا تفریق کنیم؟

چطور عبارت های گویا را با هم ضرب و تقسیم کنیم؟

چطور کسرهای مرکب را ساده کنیم؟

چطور مخرج یک کسر را گویا کنیم؟

چطور چندجمله ای ها را بر هم تقسیم کنیم؟ بخش پذیری چه زمانی اتفاق می افتد؟

چطور یک معادله گویا را حل کنیم؟

دیدگاهتان را بنویسید لغو پاسخ

آخرین مطالب وبلاگ

دنباله های عددی

تابع خطی و معادله خط

تابع و دامنه و برد آن

تعیین علامت

عبارت و معادله گویا

معادله درجه دوم

معادله

عبارت جبری

قدرمطلق

دوره ها

دسترسی سریع

دسترسی سریع

مقالات مادر