کاملترین آموزش درمورد الگوهای خطی وغیرخطی، دنباله های حسابی، هندسی و بازگشتی

دنباله، یک سری اعداد پشت سر هم هستند که ممکن است با هم رابطه داشته باشند. در این مقاله به آموزش دنباله هایی که جملات متوالی آنها اختلاف یکسانی دارند (دنباله حسابی)، دنباله هایی که نسبت جملات متوالی آنها ثابت است (دنباله هندسی) و دنباله هایی که هر جمله براساس جملات قبلی خود بدست می آیند (جملات بازگشتی) می پردازیم. هر کدام از این دنباله های قواعدی دارند که در این مقاله به آموزش کامل آن می پردازیم.

الگوهای خطی و غیر خطی

دنیای اطراف ما سرشار از الگوهای مختلفی است. به عنوان نمونه، پیدایش شبانه روز و تغییر فصول مختلف سال جلوهای از الگوی حاکم بر طبیعت است. از سوی دیگر نظم و قانونمندیهای موجود در یک الگو به خودی خود برای ما جذاب است. چه بسا ممکن است طرحهای روی یک گل آفتابگردان، شکلهای هندسی روی یک سطح کاشی کاری شده توجه شما را به خود جلب کرده میوه باشند. به طور کلی می توان گفت الگو یک ساختار منظم از اشکال، تصاویر، صداها، نمادها، وقایع یا اعداد است که ممکن است تکرار شونده یا رشد کننده یا ترکیبی از این دو باشد. مثلا الگوی $10,10,10,…$ یک الگوی تکرار شونده است. الگوی $10,15,20,…$ یک الگوی رشد کننده است. الگوی $5,10,10,20,10,10,80,…$ یک الگوی ترکیبی است.

به طور کلی اگر جمله عمومی یک الگو را داشته باشیم به معنای آگاهی داشتن از تمام جملات آن الگو است.

مثلا اگر یک الگو با جمله عمومی $c_{n}=5n+3$ داشته باشیم یعنی جمله اول دنباله به صورت $c_{1}=5(1)+3=8$ ، جمله دوم دنباله به صورت $c_{2}=5(2)+3=13$ بدست می آید.

یا اگر یک الگو با جمله عمومی $c_{n}=7n^{3}-3n^{2}+2n-5$ داشته باشیم یعنی جمله اول برابر است با $c_{1}=7(1)^{3}-3(1)^{2}+2(1)-5=7-3+2-5=1$ و جمله سوم برابر با $c_{3}=7(3)^{3}-3(3)^{2}+2(3)-5=7(27)-27+6-5=163$ است.

الگو ها را می توان به دو دسته خطی یا غیرخطی تقسیم کرد. در ادامه با هر کدام از آنها آشنا می شویم.

الگوی خطی

به طور کلی الگوهایی را که جمله عمومی آنها به صورت $t_{n}=an+b$ است ( توجه کنید جمله عمومی شبیه به معادله خط است)، الگوهای خطی می نامیم که در آن $a$ و $b$ اعداد حقیقی دلخواه و ثابت هستند. در یک الگوی خطی اختلاف هر دو جمله متوالی برابر ضریب $n$ (در اینجا $a$ ) است.

الگوی خطی همان دنباله حسابی است که در ادامه ی این مقاله به آن می پردازیم.

الگوی غیرخطی

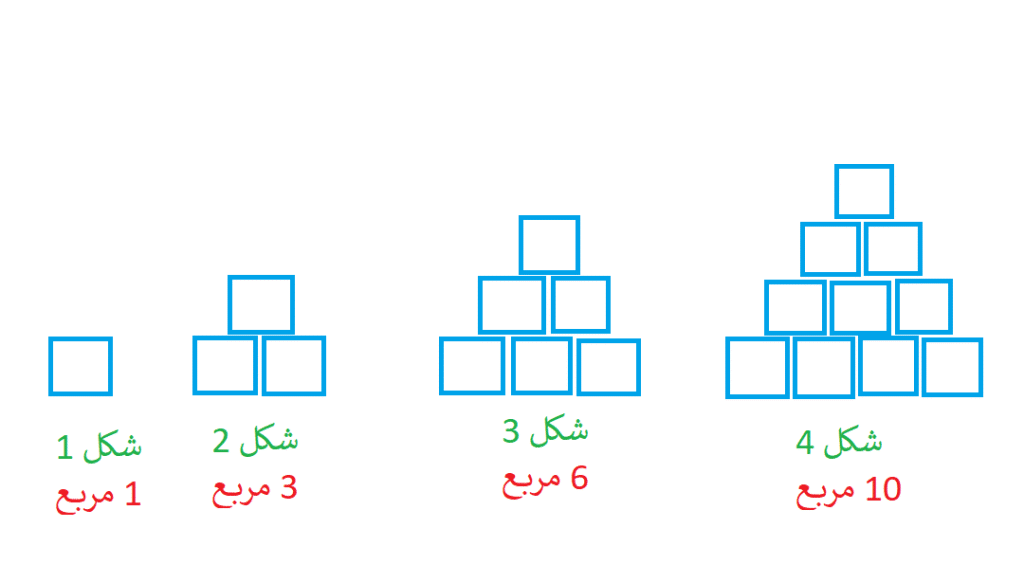
در الگوهایی که شبیه به جمله عمومی دنباله خطی نیست مثلا $n$ توان دو یا بیشتر داشته باشد یا در مخرج یک کسر یا زیر رادیکال باشد آنگاه الگو، غیرخطی است. در ادامه چند دنباله غیرخطی مثال می زنیم.

دنباله شکل بالا یک دنباله مثلثی است. تعداد مربع ها در شکل ها به صورت $1,3,6,10,15,21,…$ است. به طور کلی شکل $n$ ام دنباله دارای $\frac{n(n+1)}{2}$ مربع است.

دنباله شکل بالا یک دنباله مربعی را نشان می دهد چراکه تعداد مربع ها در هر شکل به صورت $1,4,9,16,25,…$ می باشد . در واقع تعداد مربع ها در هر شکل مجذور یا مربع یا توان دوم شماره شکل است که می توان آن را با $n^{2}$ نشان دهیم.

انواع دنباله ها: بازگشتی، حسابی و هندسی

هر تعداد عدد را که پشت سر هم قرار می گیرند، یک دنباله می نامیم این اعداد، جملات دنباله نامیده می شوند. در واقع اگر $a$ تابعی از اعداد طبیعی به اعداد حقیقی باشد اعضای برد این تابع می تواند دنباله ای از اعداد را تولید کند که به ترتیب، جمله اول آن را با $a(1)$ جمله دوم را با $a(2)$ و به همین ترتیب جمله $n$ ام آن را با $a(n)$ در نظر می گیریم.

معمولا جملات دنباله را به جای $a(n)$ با $a_{n}$ نشان می دهند که آن را جمله $n$ ام جمله عمومی دنباله یا ضابطه دنباله می نامند.

مثلا اگر یک دنباله با جمله عمومی $a_{n}=n^{3}+3n^{2}-5n+9$ داشته باشیم. جمله اول این دنباله برابر است با $a_{1}=(1)^{3}+3(1)^{2}-5(1)+9=1+3-5+9=8$ و جمله دوم این دنباله برابر است با $a_{2}=(2)^{3}+3(2)^{2}-5(2)+9=8+12-10+9=19$ به همین ترتیب می توانیم همه جملات دنباله را با استفاده از جمله عمومی داده شده بدست آوریم.

در ادامه سه نوع دنباله را بررسی می کنیم.

دنباله بازگشتی

دنباله بازگشتی دنباله ای است که هر جمله از آن با استفاده از جملات قبلی بدست آید. دنباله فیبوناتچی یک نوع دنباله بازگشتی است. در این دنباله جمله اول و جمله دوم برابر با یک است و از جمله سوم به بعد هر جمله برابر با مجموع دو جمله قبلی است. می توانیم بنویسیم:

$\begin{cases} a_{1}=1 \\ a_{2}=1 \\ a_{n}=a_{n-1}+a_{n-2} & n \ge 3 \end{cases}$

در نتیجه دنباله فیبوناتچی به صورت $1,1,2,3,5,8,13,…$ می باشد.

البته دنباله فیبوناتچی علاوه بر اینکه می توان به صورت دنباله بازگشتی نوشت می توان به صورت یک فرمول کلی هم هر جمله را پیدا کرد. در واقع جمله

عمومی دنباله فیبوناتچی برابر است با $a_{n}=\frac{p^{n}-q^{n}}{\sqrt{5}}$ که در آن $p=\frac{1+\sqrt{5}}{2}$ و $q=\frac{1-\sqrt{5}}{2}$ هستند.

مثلا می توان یک دنباله بازگشتی به صورت زیر تعریف کرد.

$\begin{cases} a_{1}=1 \\ a_{2}=3 \\ a_{n}=a_{n-1}+2a_{n-2} & n \ge 3 \end{cases}$

در این صورت دنباله به صورت $1,3,5,11,21,43,85,…$ بدست می آید. در نتیجه

$a_{3}=a_{2}+2(a_{1})=3+2(1)=5$

به همین ترتیب سایر جملات دنباله را بدست می آوریم.

دنباله حسابی

دنباله ای که در آن هر جمله ( به جز جمله اول) با اضافه شدن عددی ثابت به جمله قبل از خودش به دست می آید، دنباله حسابی نامیده می شود و به آن عدد ثابت، قدرنسبت دنباله می گویند.

نکته1: یک دنباله حسابی دنباله ای به صورت زیر است

$a,a+d,a+2d,a+3d,…$

که در آن $a$ جمله اول و عدد ثابت $d$ اختلاف مشترک جملات دنباله است. جمله $n$ ام این دنباله با رابطه زیر معرفی می شود.

$a_{n}=a_{1}+(n-1)d$

نکته 2: $d$ را اختلاف مشترک دنباله حسابی می نامند زیرا همه جملات دنباله در یک ویژگی مشترک اند و آن اینکه اختلاف هر دو جمله متوالی از آنها مقدار ثابت $d$ است.

نکته 3: اگر جمله عمومی یک دنباله حسابی را بنویسیم، شبیه به یک معادله خط خواهد شد . هر دنباله حسابی یک تابع خطی است که شیب خط، همان اختلاف مشترک جملات دنباله، یعنی $d$ است و به عکس، دنباله ساخته شده از یک تابع خطی نیز جملات یک دنباله حسابی را مشخص می کند.

مثلا دنباله اعداد $-5,-2,1,4,7,10,…$ یک دنباله حسابی یا یک الگوی خطی است. چراکه اختلاف هر دو جمله متوالی برابر با عدد $3$ است و جمله اول این دنباله برابر با $-5$ است. بنابراین می توان جمله عمومی دنباله را به صورت زیر نوشت:

$a_{n}=-5+3(n-1)=3n-8$

بنابراین می بینیم اگر بدانیم یک دنباله حسابی است یا دارای الگوی خطی است با داشتن جمله اول و قدرنسبت دنباله می توانیم جمله عمومی دنباله را بدست آوریم و در نتیجه می توانیم همه ی جملات دنباله را بدست آوریم.

نکته4 : اگر $a,b,c$ سه جمله متوالی از یک دنباله حسابی باشند آنگاه $b$ (جمله وسط) واسطه حسابی دو جمله دیگر یعنی $a,c$ است. این به این معناست که

$2b=a+c$

مثلا در دنباله $-5,-2,1,4,7,…$ جمله دوم بین جمله اول و سوم است پس می توانیم بنویسیم $2\times (-2)=-5+1$ یا چون جمله سوم بین جمله دوم و چهارم است می توانیم بنویسیم $2\times 1=-2+4$ می بینیم نکته 4 برای هر سه جمله متوالی از دنباله حسابی صحیح می باشد.

نکته 5: مجموع $n$ جمله اول یک دنباله حسابی با جمله عمومی $a_{n}=a_{1}+(n-1)d$ از رابطه زیر بدست می آید :

$S=\frac{n(2a_{1}+(n-1)d)}{2}$

$or \,\,\,\,\,S=\frac{n(a_{1}+a_{n})}{2}$

مثلا در دنباله $-5,-2,1,4,7,…$ اگر بخواهیم مجموع 100 جمله اول را بدست آوریم با توجه به نکته 5 از فرمول زیر استفاده می کنیم:

$S=\frac{n(2a_{1}+(n-1)d)}{2}$

$= \frac{100(2(-5)+(100-1)(3))}{2}$

$=\frac{100(-10+297)}{2}=14350$

نکته6: برای بدست آوردن مجموع اعداد طبیعی $1$ تا $n$ باید به این توجه کنیم که فاصله بین هر دو جمله متوالی برابر یک است. بنابراین این دنباله یک دنباله حسابی است. جمله اول برابر $1$ است و جمله آخر برابر $n$ بنابراین طبق نکته 5 مجموع $n$ جمله اول به صورت زیر بدست می آید:

$1+2+3+…+n\,\,\,\,\rightarrow$

$S=\frac{n(a_{1}+a_{n}}{2}=\frac{n(1+n)}{2}$

دنباله هندسی

دنباله ای است که در آن هر جمله ( به جز جمله اول ) از ضرب جمله قبل از خودش در عددی ثابت و غیرصفر به دست می آید. این عدد ثابت را قدرنسبت دنباله می نامیم . جمله اول هم باید غیرصفر باشد.در واقع می توان گفت یک دنباله هندسی، دنباله ای به صورت $a,ar,ar^{2},ar^{3},…$ است که در آن $a\neq 0$ جمله اول و $r\neq 0$ نسبت مشترک دنباله است. جمله $n$ ام این دنباله هندسی از رابطه زیر بدست می آید:

$a_{n}=a_{1}r^{n-1}$

مثلا دنباله اعداد $5,15,45,135,…$ یک دنباله هندسی است. چراکه نسبت هر دو جمله متوالی برابر با عدد $3$ است و جمله اول این دنباله برابر با $5$ است. بنابراین می توان جمله عمومی دنباله را به صورت $a_{n}=5\times 3^{n-1}$ نوشت. بنابراین می بینیم اگر بدانیم یک دنباله هندسی است. با داشتن جمله اول و قدرنسبت دنباله می توانیم جمله عمومی دنباله را بدست آوریم و در نتیجه می توانیم همه ی جملات دنباله را بدست آوریم.

نکته7 : اگر $a,b,c$ سه جمله متوالی از یک دنباله هندسی باشند آنگاه $b$ (جمله وسط) واسطه هندسی دو جمله دیگر یعنی $a,c$ است. این به این معناست که $b^{2}=ac$ .

مثلا دنباله اعداد $5,15,45,135,…$ یک دنباله هندسی است. جمله دوم بین جمله اول و سوم است پس می توانیم بنویسیم $15^{2}=5\times 45$ یا چون جمله سوم بین جمله دوم و چهارم است می توانیم بنویسیم $45^{2}=15\times 135$ می بینیم نکته 7 برای هر سه جمله متوالی از دنباله هندسی صحیح می باشد.

نکته 8: مجموع جملات دنباله هندسی با جمله اول $a$ و قدر نسبت $r$ و تعداد جملات $n$ در واقع مجموع $n$ جمله اول یک دنباله هندسی با جمله عمومی $a_{n}=a_{1}r^{n-1}$ از رابطه زیر بدست می آید :

$S=\frac{a_{1}(1-r^{n})}{1-r}$

مثلا دنباله اعداد $5,15,45,135,…$ یک دنباله هندسی است. برای بدست آوردن مجموع پنج جمله اول این دنباله از نکته 8 استفاده می کنیم.

$S=\frac{a_{1}(1-r^{n})}{1-r}=\frac{5(1-3^{5}}{1-3}$

$=\frac{5(-242)}{-2}=605$

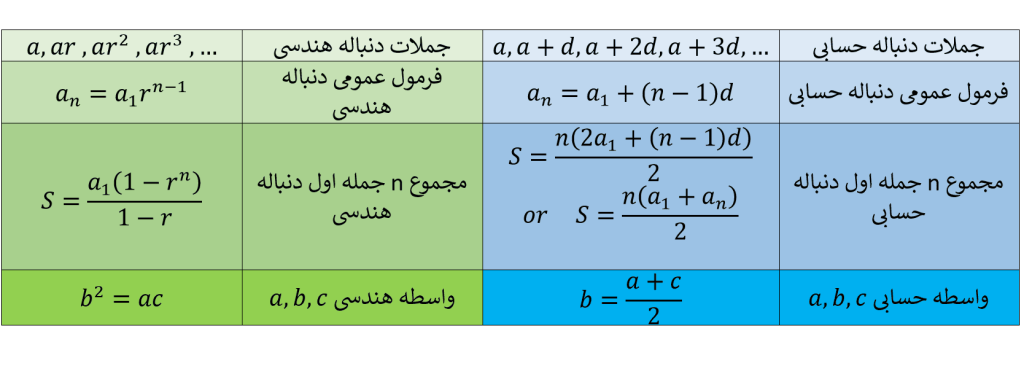
همه ی فرمول های دنباله را به صورت یکجا می توانید در جدول زیر ببینید:

جمع بندی

در این مقاله به آموزش الگوهای خطی و غیر خطی و همچنین دنباله حسابی و هندسی و بازگشتی پرداختیم به طوری که جملات عمومی هر کدام و فرمول جمع جملات هر کدام را بیان کردیم. امیدواریم این مقاله برای شما مفید بوده باشد. اگر تمایل دارید که به صورت جامع و بهمراه نمونه سوالات کنکور و نهایی در سالهای مختلف این مطالب را بیاموزید دوره جبر معادله تابع فرامث را تهیه کنید. لطفا در قسمت کامنت ها نظرات و پیشنهادات خود را در مورد مقاله دنباله های عددی بیان کنید.

کاملترین آموزش درمورد الگوهای خطی وغیرخطی، دنباله های حسابی، هندسی و بازگشتی

الگوهای خطی و غیر خطی

انواع دنباله ها: بازگشتی، حسابی و هندسی

دیدگاهتان را بنویسید لغو پاسخ

آخرین مطالب وبلاگ

دنباله های عددی

تابع خطی و معادله خط

تابع و دامنه و برد آن

تعیین علامت

عبارت و معادله گویا

معادله درجه دوم

معادله

عبارت جبری

قدرمطلق

دوره ها

دسترسی سریع

دسترسی سریع

مقالات مادر