کامل ترین مجموعه از انواع توابع، ضابطه، دامنه، برد، نمودار و ویژگی های آنها
انواع توابع شامل تابع ثابت، تابع همانی، تابع پلکانی، تابع علامت، تابع جز صحیح، تابع خطی، تابع سهمی، تابع درجه سه، تابع چندجمله ای، تابع گویا، تابع هموگرافیک، تابع رادیکالی، تابع نمایی، تابع لگاریتمی و در نهایت تابع چندضابطه ای را در این مقاله آموزش دادیم. این آموزش شامل تعریف این توابع، بیان دامنه و بردشان و همچنین همه ی ویژگی ها و خواص این توابع می باشد. برای اینکه نمودار این توابع را به طور اختصاصی بیاموزید می توانید به مقاله رسم نمودار توابع مراجعه کنید. اما اگر می خواهید همه ی توابعی که در سال های تحصیلی تان در مدرسه در متوسطه اول و در متوسطه دوم رشته های تجربی ریاضی و انسانی می خوانید بیاموزید این مقاله را از دست ندهید تا همه ی اطلاعات لازم را بطور خلاصه از این مقاله یعنی مقاله انواع توابع، دریافت کنید.
انواع توابع: ثابت، همانی، خطی، چندضابطه ای ،پلکانی، جزصحیح، علامت، نمایی، لگاریتمی، قدرمطلقی، گویا، هموگرافیک
انواع توابعی که بهتر است بشناسید را بهمراه نمودار این توابع در ادامه می بینید:
تابع ثابت
تابع 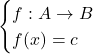
برد تابع است، تابع ثابت می نامند. در تابع ثابت، برد تابع تنها شامل یک عضو است. شکل زیر تابع ثابت را نشان می دهد:
مثال: اگر تابع ثابت باشد مقادیر زیر را بدست آورید.
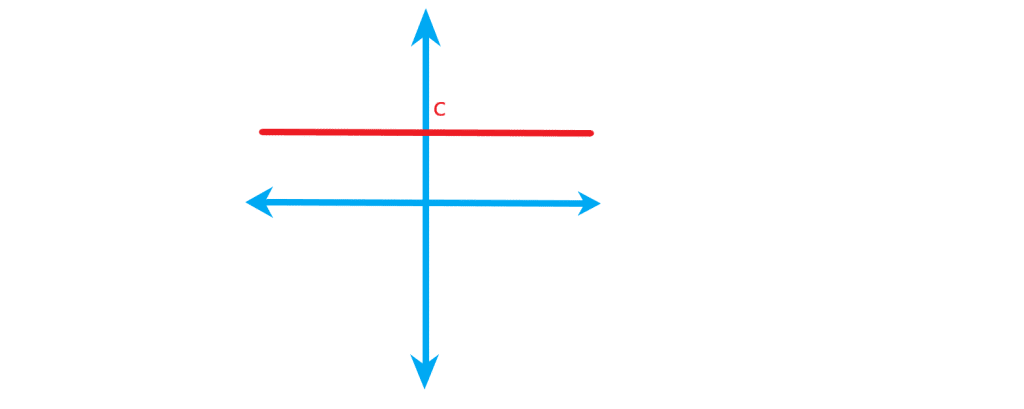
تابع همانی
اگر دامنه و برد تابع برابر باشند و هر عضو از دامنه تابع دقیقا به همان عضو در برد نظیر شود، تابع را همانی می نامند. اگر دامنه تابع همانی را در نظر بگیریم، نمودار آن همان خط
است که با ضابطه
هم نمایش داده می شود. با توجه به ضابطه تابع، در تابع همانی دامنه و برد همواره با یکدیگر برابرند. از لحاظ هندسی نمودار این تابع نیمساز ناحیه اول و سوم مختصات است.
مثال: اگر همانی باشد مقادیر زیر را بدست آورید.
تابع چند ضابطه ای
توابعی که در بخش های مختلف دامنه ، ضابطه های مختلف دارند، توابع چندضابطه ای نامیده می شوند؛ مثلا اگر یک تابع از دو ضابطه پیروی کند، یک تابع دو ضابطه ای نامیده می شود.
پلکانی
در تابع چند ضابطه ای که هر ضابطه مقدار تابع، عددی ثابت است تابع پلکانی می نامند.
به طور کلی توابعی که بتوان دامنه آنها را به تعدادی بازه تقسیم کرد به گونه ای که تابع روی هر کدام از این بازه ها ثابت باشد ، تابع پله ای می نامند.
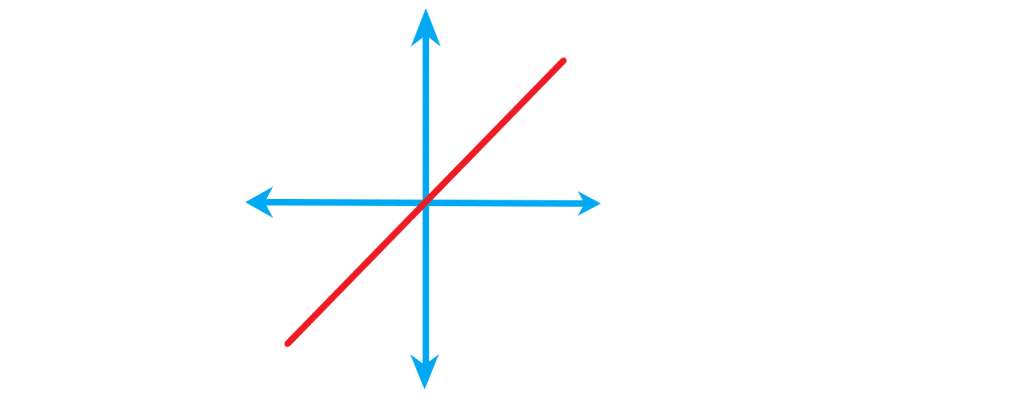
تابع علامت
یک نوع تابع پلکانی تابع علامت یا تابع می نامند.
دامنه تابع علامت شامل همه ی اعداد حقیقی و برد آن فقط شامل سه عدد یعنی می باشد.
مثال: مقادیر زیر را بدست آورید.
جز صحیح
یک نوع تابع پلکانی تابع جز صحیح است. این تابع به هر عدد صحیح خود همان عدد و به تمام اعداد میان دو عدد صحیح متوالی
و
، عدد صحیح
(عدد کوچکتر) را نسبت می دهد. ضابطه این تابع را با
(بخوانید جز صحیح
) معرفی می کنند .
- مشهورترین تابع پله ای تابع جز صحیح است.
- جز صحیح هر عدد غیر صحیح، برابر است با اولین عدد صحیح سمت چپ آن روی محور اعداد.
- گونه خاصی از توابع پله ای که دارای کاربرد های زیادی نیز هست تابع جز صحیح نام دارد.
مثال: مقادیر زیر را بدست آورید.
تابع خطی
هر تابع که در آن
یک تابع خطی نامیده می شود.
اگر دو نقطه از یک خط را داشته باشیم معادله خط از راه حل زیر بدست می آید:
برای رســم نمودار تابع خطی دو نقطه از نمودار تابع را در دســتگاه مختصات مشخص می کنیم و سپس آن دو نقطه رابه وسیله خطی به هم وصل می کنیم.
مثال: اگر یک تابع خطی باشد که از دو نقطه
بگذرد ضابطه تابع خطی را بدست آورید.
برای دانستن اطلاعات کامل از تابع خطی و رسم آن و حل دستگاه با دو تابع خطی به مقاله ی معادله خط و حل دستگاه مراجعه فرمائید.
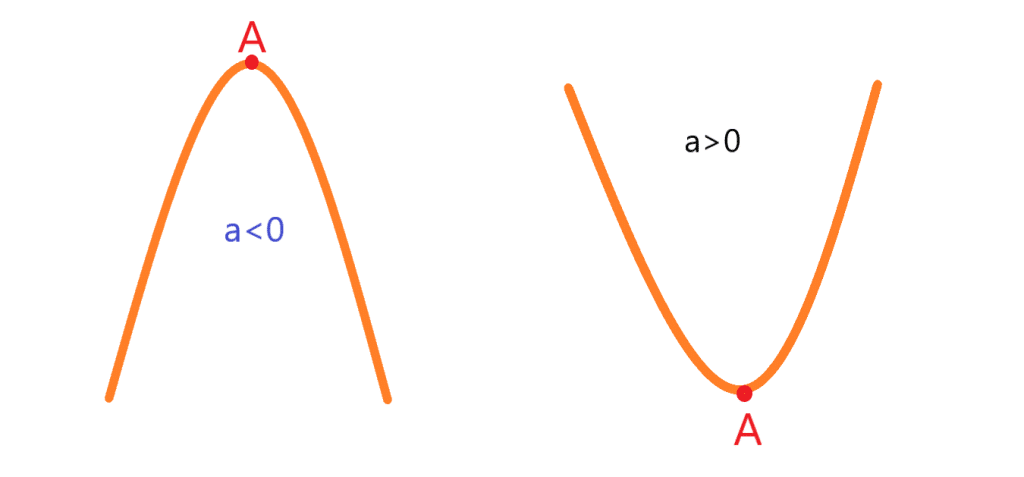
تابع درجه دو یا سهمی
هر تابع که در آن
یک تابع سهمی نامیده می شود.
اگر شکل سهمی رو به بالا است و سهمی در نقطه راس خود کمترین مقدار است.
اگر شکل سهمی رو به پایین است و سهمی در نقطه راس خود بیشترین مقدار است.
شکل سهمی در حالت کلی یکی از دو شکل زیر است:
نقطه در شکل های بالا راس سهمی نام دارد. اگر
باشد نقطه
پایین ترین نقطه سهمی است و مینیممم سهمی نام دارد و اگر
باشد نقطه
بالا ترین نقطه سهمی است و ماکزیمم نام دارد. همچنین خط عمودی که از راس سهمی می گذرد ، خط تقارن سهمی نامیده می شود. طول راس سهمی برابر
است و خط تقارن آن خطی با معادله
هست.
و اگر نمایش جبری سهمی به صورت باشد، مختصات راس سهمی
است و خط تقارنی با معادله
دارد.
مثال: ماکزیمم یا مینیمم تابع با ضابطه را در صورت وجود بدست آورید.
جواب: چون منفی است پس دهانه سهمی رو به پایین است و این سهمی ماکزیمم دارد . از طرفی می دانیم تابع به ازای
بیشترین مقدار خود را خواهد داشت که برابر است با
. پس نقطه
راس سهمی و نقطه ماکزیمم آن است. در نتیجه مقدار ماکزیمم سهمی برابر 4 است.
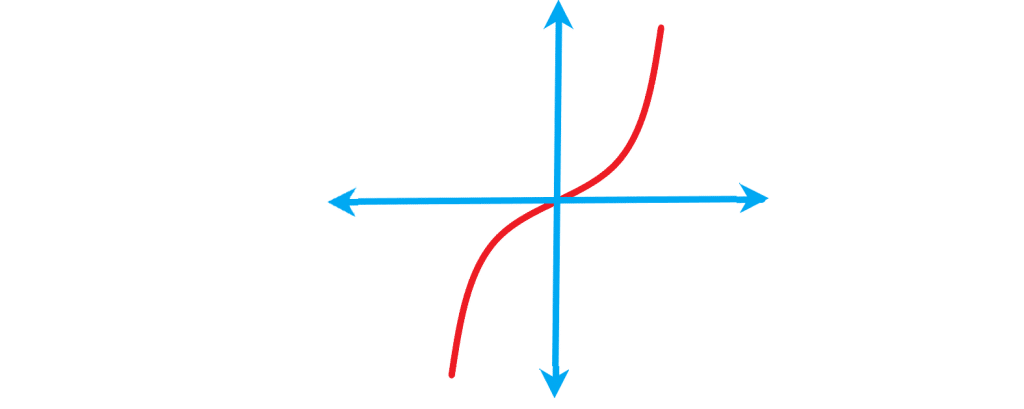
تابع درجه سه
تابع چندجمله ای با ضابطه که
یک تابع درجه 3 است که در اینجا به طور خاص تابع
را نشان می دهیم . دامنه و برد این تابع
است. این تابع یک به یک و وارون پذیر است.
توابع چند جمله ای
هر تابع با ضابطه را یک تابع خطی می نامیم. اگر
تابع به صورت
در می آید که آن را تابع ثابت می نامبم. توابع ثابت و توابع خطی، مثال هایی از توابع چندجمله ای با درجه های صفر و یک هستند.
هر تابع به صورت را که در آن
اعداد حقیقی و
یک عدد صحیح نامنفی و
باشد، یک تابع چندجمله ای از درجه می نامیم. دامنه توابع چند جمله ای مجموعه اعداد حقیقی است.
- تابع ثابت یک تابع چند جمله ای از درجه صفر و تابع همانی از درجه یک است
- تابع خطی
تابع چندجمله ای درجه یک است.
- سهمی به معادله
یک تابع چند جمله ای از درجه دو است.
- برای
درجه تعریف نمی شود.
قضیه تقسیم برای چند جمله ای ها
اگر و
چندجمله ای باشند و درجه
از صفر بزرگتر باشد، آنگاه چندجمله ای های منحصر بفرد
و
وجود دارند به طوری که :
که در آن (که در این صورت چندجمله ای
بر چندجمله ای
بخش پذیر است) یا درجه
از درجه
کمتر است.(تقسیم چندجمله ای ها را به طور کامل تر می توانید در مقاله عبارت و معادله گویا بخوانید)
قضیه : باقی مانده تقسیم جندجمله ای بر
عبارت است از
.
نکته: یک اتحاد داریم که در آن چند جمله ای بر
بخش پذیر است و خارج قسمت برابر است با
.
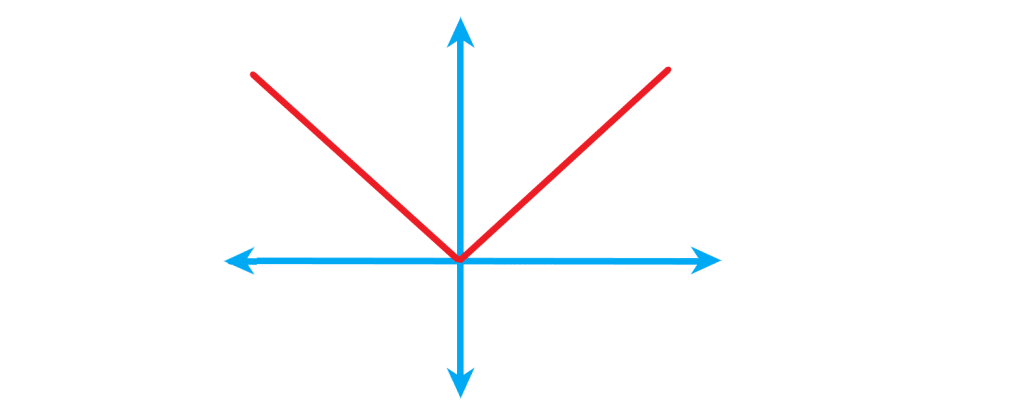
تابع قدرمطلقی
تابعی که هر مقدار در دامنه را به قدر مطلق آن در برد نظیر می کند، تابع قدرمطلق نامیده می شود. تابع قدرمطلق را با نشان می دهند. ( اگر اطلاعات کاملی از تعریف تابع قدرنمطلق حل معادله و نامعادله قدرمطلقی می خواهید دریافت کنید لطفا به مقاله قدرمطلق مراجعه کنید)
تابع با ضابطه ، تابع قدر مطلق نامیده می شود و مطابق تعریف :
دامنه تابع برابر اعداد حقیقی و برد آن برابر اعداد حقیقی نامنفی است.
مثال: تابع را به صورت چند ضابطه ای بنویسید.
توابع گویا
هر تابع به شکل را یک تابع گویا می نامیم که در آن
و
چند جمله ای هستند و چند جمله ای
صفر نیست.
دامنه یک تابع گویا مجموعه ی همه ی اعدادی است که مخرج آن را صفر نمی کند. اما ممکن است دامنه را به مجموعه های دیگری محدود کنیم. دامنه تابع را به
نمایشی می دهیم.
مثلا یک تابع گویاست و
یک تابع گویا نیست.
دامنه توابع گویا
مخرج هیچ کسری نمی تواند صفر باشد. به طور کلی اعدادی که مخرج کسر مربوط به ضابطه ی یک تابع گویا را صفر کنند، عضو دامنه آن تابع نیستند. ( اگر قبل از توابع گویا می خواهید در مورد اعداد گویا و عبارت و معادلات گویا بدانید لطفا به مقاله هر کدام رجوع کنید)
مثلا در تابع گویای دامنه تابع را به این صورت بدست می آوریم که در گام اول می بینیم چه اعدادی مخرج را صفر می کنند برای اینکار از چیزهایی که در مقاله معادله درجه دوم خواندیم استفاده می کنیم.
پس دامنه تابع به صورت بدست می آید.
اگر می خواهید شکل این تابع را ببینید می توانید از سایت با حساب استفاده کنید.
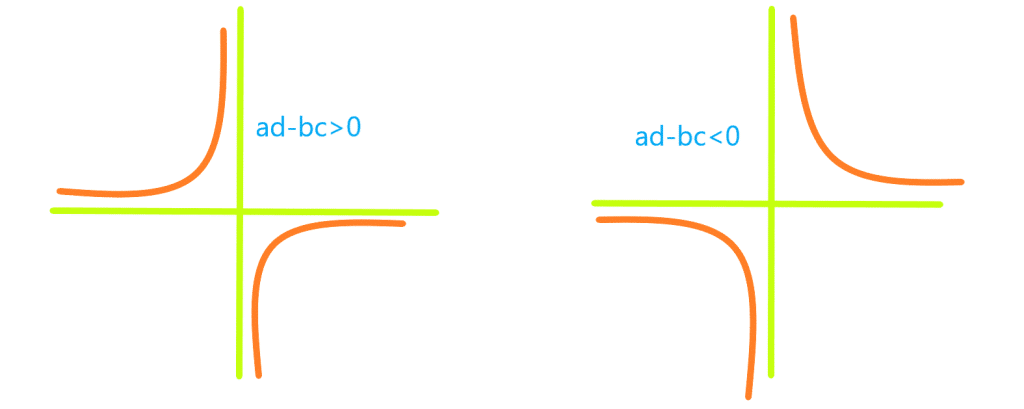
تابع هموگرافیک
تابع هموگرافیک نسبت یک دوجمله ای درجه اول به یک دو جمله ای درجه اول دیگر است. این تابع را به صورت کلی به صورت نشان می دهند که در آن
است. این تابع تحت شرایطی که در ادامه بیان می شود به تابع خط راست یا تابع ثابت تبدیل می شود.
اگر و
باشد تابع به صورت
تبدیل می شود که نشان دهنده ی معادله ی یک خط راست است.
اگر و
و
باشد این تابع به یک تابع ثابت تبدیل می شود.
همچنین مجانب های تابع هموگرافیک به صورت زیر بدست می آید:
بنابراین مجانب افقی این تابع است. و
مجانب قائم این تابع است
نمودار یک تابع هموگرافیک با توجه به مجانب هایش به صورت شکل زیر است:
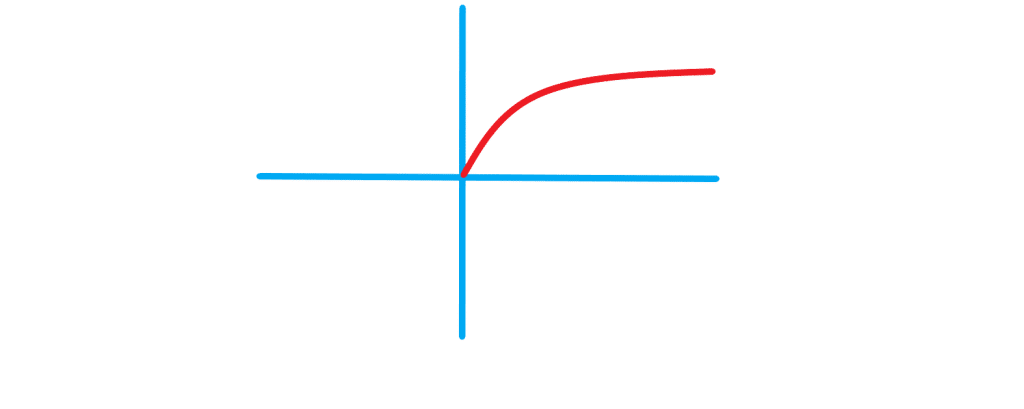
توابع رادیکالی (تابع ریشه دوم)
تابعی را که هر عدد نامنفی را به ریشه دوم نامنفی آن نسبت می دهد تابع ریشه دوم می نامند و به صورت یا
نمایش می دهند.
نمودار تابع به شکل زیر است و دامنه و برد تابع بازه ی می باشد. تابع
یک تابع رادیکالی می باشد.
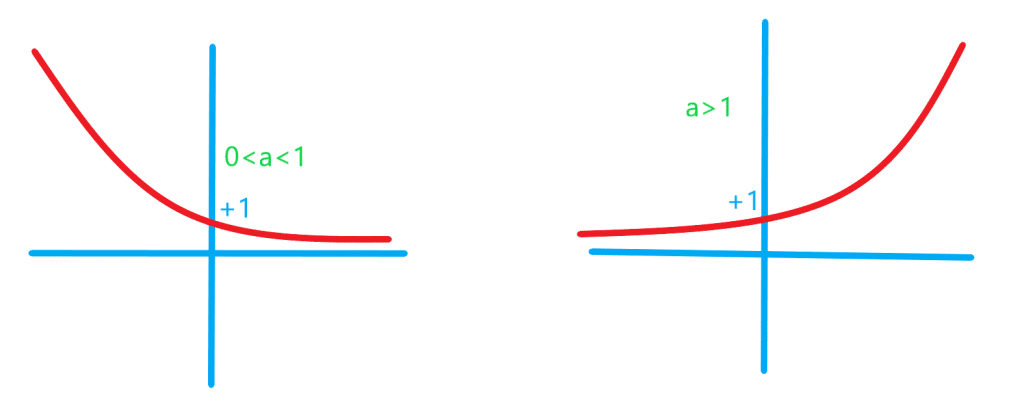
معادله و تابع نمایی
هر تابع با ضابطه که در آن
عددی مثبت و مخالف یک است را یک تابع نمایی می گویند.
در حالت کلی هر تابع با ضابطه رفتار نمایی دارد.
حرف معرف پایه و حرف
معرف نما یا توان است. دامنه و برد تابع نمایی
برای
برابر است با:
در تابع نمایی اگر
باشد، وقتی
بزرگ می شود، مقدار
کم می شود.
نمودار توابع با ضابطه های و
که
نسبت به محور عرض ها قرینه اند. این دو تابع یک به یک اند چون هر خط موازی محور طول ها نمودار آنها را حداکثر در یک نقطه قطع می کند.
رشد نمایی
معادله کلی رشد نمایی، به صورت است که در آن
بیانگر مقدار نهایی ،
بیانگر مقدار اولیه،
بیانگر میزان رشد ( تغییرات بر حسب اعشار) و
بیانگر زمان است.
نرخ رشد: به میزان افزایش یک کمیت )نظیر جمعیت( در واحد زمان، نرخ رشد گفته میشود.
زوال نمایی
معادله کلی زوال نمایی ، به صورت است که در آن
بیانگر مقدار نهایی ،
بیانگر مقدار اولیه،
بیانگر میزان نزول ( تغییرات بر حسب اعشار) و
بیانگر زمان است.
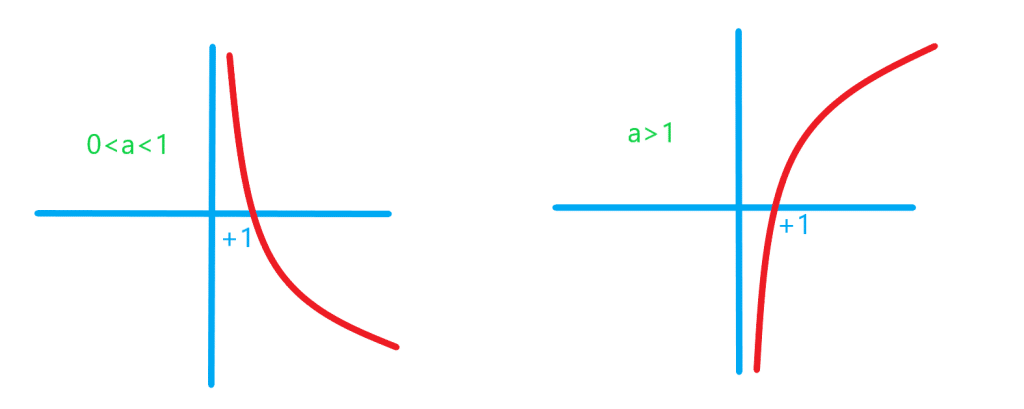
تابع لگاریتمی
اگر عددی مثبت و مخالف یک باشد تابع نمایی
یک به یک است و از این رو دارای تابع وارون
است که تابع لگاریتمی پایه
نامیده می شود و با نماد
نشان داده می شود.
تذکر:
شکل تابع لگاریتمی را در ادامه می توانید ببینید:
ویژگی های لگاریتم را در زیر می توانید ببینید:
نکات لگاریتم :
- لگاریتم اعداد مثبت کمتر از 1 همواره عددی منفی است.
- لگاریتم اعداد منفی تعریف نمی شود.
- تابع لگاریتم تابعی یک به یک است.
- تابع لگاریتم محور عرض ها را قطع نمی کند و محور طول ها را قطع می کند.
جمع بندی
در این مقاله به بیان انواع توابع و دامنه و برد آنها پرداخته شده است. از انواع توابعی که در این مقاله ذکر شده است تابع ثابت، تابع همانی، تابع چند ضابطه ای، تابع پلکانی، تابع علامت، تابع جز صحیح، تابع خطی، تابع سهمی، تابع درجه سه، تابع چند جمله ای، تابع گویا، تابع قدرمطلقی، تابع هموگرافیک، تابع نمایی، رشدو زوال نمایی، تابع لگاریتمی می باشند. برای رسم نمودار این توابع می توانید به مقاله ی نمودار توابع مراجعه کنید. برای خواندن درباره یک به یک و وارون پذیر بودن و ضابطه ی وارون توابع در صورت وجود می توانید به مقاله ی وارون توابع یک به یک مراجعه کنید و برای تشخیص صعودی و نزولی بودن این توابع به مقاله ی توابع صعودی و نزولی مراجعه فرمایید. همچنین می توانید برای اینکه بفهمید با جمع و تفریق یا ضرب و تقسیم توابع به چه توابع جدیدی می رسید و به چه نکاتی باید توجه کنید به مقاله ی اعمال جبری توابع مراجعه کنید. امیدواریم از خواندن این مقاله بهره لازم را برده باشید اگر تمایل دارید که به صورت جامع و بهمراه نمونه سوالات کنکور و نهایی در سالهای مختلف این مطالب را بیاموزید دوره جبر معادله تابع فرامث را تهیه کنید. لطفا ما را از نظرات ارزشمند خودتان درباره مقاله انواع توابع در قسمت کامنت ها بهره مند کنید.

![Rendered by QuickLaTeX.com \[f(x)=\begin{cases}1 & x> 0 \\ 0 & x=0 \\ -1 & x < 0 \end{cases}\]](https://faramath.com/core/ql-cache/quicklatex.com-4aafd3068d9ccafed93b616555817e30_l3.png)
![Rendered by QuickLaTeX.com \[f(x)=\begin{cases} x & x \ge 0 \\ -x & x < 0 \end{cases}\]](https://faramath.com/core/ql-cache/quicklatex.com-27626e9fe158138bbe1d4cdcfc040c3a_l3.png)
![Rendered by QuickLaTeX.com \[f(x)=\begin{cases} -2x+4 & -2x+4 \ge 0 \\ -(-2x+4) & -2x+4 < 0 \end{cases} =\begin{cases} -2x+4 & x \le 2 \\ 2x-4 & x > 2 \end{cases}\]](https://faramath.com/core/ql-cache/quicklatex.com-549e6bb578784c3adf4f0dffd1cd3aab_l3.png)
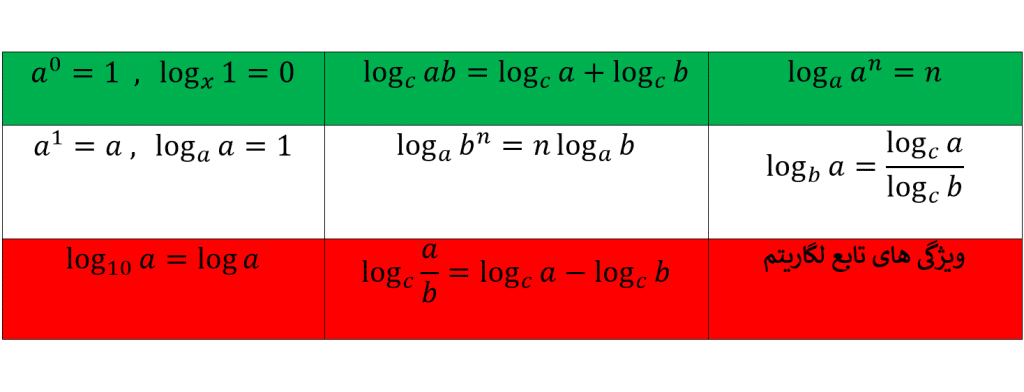

2 پاسخ
سلااااام خیلی ممنونم اصلا باورم نمیشه !!!
چقدر همه چیز اینجا کامله واقعا همه توابع سه سال رو گفتید؟
همه رو با هم می بینم احتمال اینکه با هم قاطی شون کنم خیلی کم میشه
سلام. خوشحالم راضی بودی عزیزم