فرامث دات کام
حساب کاربری تو
برای ورود یا ثبت نام بیا اینجا
سبد خریدت اینجاست

اگر می خواهید همه چیز را در مورد دایره بدانید اصلا این مقاله را از دست ندهید

دایره مجموعه نقاطی در صفحه است که از یک نقطه ثابت به یک فاصله است. در این مقاله در مورد دایره می خوانیم، اینکه یک نقطه در چه وضعیتی نسبت به دایره قرار دارد، یک خط نسبت به دایره در چه وضعیتی قرار دارد، چه زاویه هایی با کمک دایره تعریف می شود، وضعیت دو دایره نسبت بهم چگونه بررسی می شود و در نهایت روابط طولی در دایره را بررسی می کنیم و مقاله را با معادله دایره و نحوه تحلیل و نوشتن آن به پایان می رسانیم.

اگر نیاز به دانستن مطالبی درباره زاویه، صفحه دارید به مقاله هندسه تحلیلی مراجعه کنید و اگر می خواهید همه چیز را درباره خط و معادله خط بدانید ب مقاله مربوطه مراجعه نمایید.

دایره چگونه شکلی است؟

مجموعه ی تمام نقاطی در صفحه  که از نقطه مشخص مثل O فاصله ی R دارند دایره ای به مرکز O و شعاع R را تشکیل می دهند. این دایره را به صورت C(O,R) نشان می دهند.

یک دایره به مرکز O و شعاع R

یک نقطه چه وضعیتی می تواند نسبت به دایره داشته باشد؟

نقطه A روی دایره به مرکز O و شعاع R است اگر وفقط اگر فاصله A از O برابر با R باشد. ( اگر می خواهید بدانید اگر و فقط اگر به چه معناست به مقاله گزاره مراجعه کنید)  به طور کلی می توان گفت:

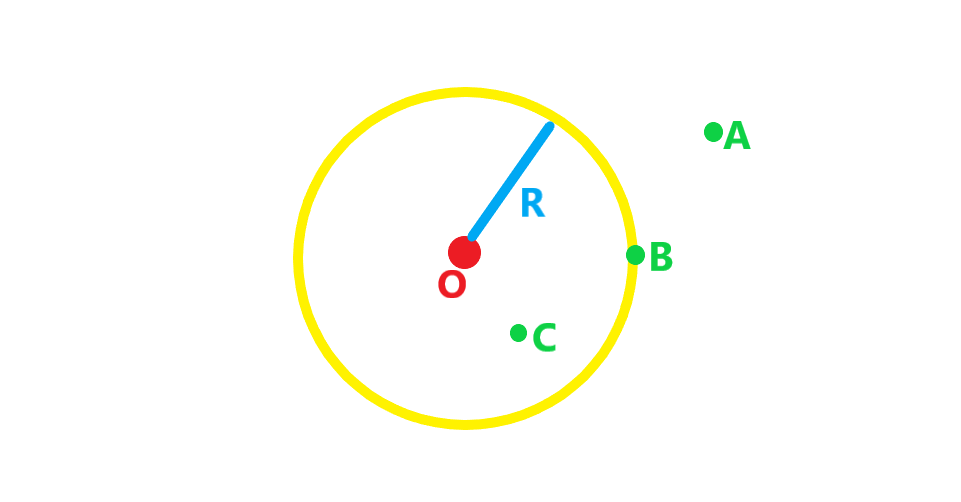
  • اگر نقطه ای روی دایره باشد فاصله آن نقطه تا مرکز دایره برابر شعاع دایره است. مثل B
  • اگر نقطه ای بیرون دایره باشد فاصله آن نقطه تا مرکز دایره از شعاع دایره بزرگتر است. مثل A
  • اگر نقطه ای درون دایره باشد فاصله آن نقطه تا مرکز دایره کمتر از شعاع دایره است. مثل C
  • اگر فاصله نقطه ای تا مرکز دایره به اندازه شعاع باشد آنگاه نقطه روی محیط دایره قرار دارد. مثل B
  • اگر فاصله نقطه ای تا مرکز دایره از شعاع بزرگتر باشد آنگاه نقطه بیرونِ دایره قرار دارد. مثل A
  • اگر فاصله نقطه ای تا مرکز دایره از شعاع کوچکتر باشد آنگاه نقطه درونِ دایره قرار دارد. مثل C
وضعیت نقطه و دایره نسبت به هم

یک نقطه چه وضعیتی می تواند نسبت به دایره داشته باشد؟

خط و دایره سه حالت ممکن است داشته باشند. خط بیرون دایره باشد خط دایره را قطع کند یا خط بر دایره مماس باشد:

  • درحالتی که خط و دایره هیچ نقطه اشتراکی نداشته باشند خط بیرون دایره است. در این حالت فاصله مرکز دایره از خط بیشتر از شعاع است. مثل d^{``}
  • اگر خط و دایره فقط در یک نقطه اشتراک داشته باشند اصطلاحا می گویند خط بر دایره مماس است. در این حالت فاصله مرکز دایره از خط به اندازه شعاع است.  مثل d
  • اگر خط و دایره دو نقطه اشتراک داشته باشند خط و دایره متقاطع اند که اصطلاحا می گوییم که خط نسبت به دایره قاطع است. در این حالت فاصله مرکز دایره از خط کمتر از شعاع است. مثل d^{'}

نکته: یک خط و دایره بر هم مماس اند اگر و تنها اگر این خط در نقطه تماس  با دایره بر شعاع آن نقطه عمود باشد. (برای دانستن مفهوم ” اگر و تنها اگر ” لطفا به مقاله گزاره مراجعه فرمائید.)

حالت های خط و دایره نسبت به هم

دایره شامل چه قسمت هایی است؟

دایره اجزای متفاوتی دارد که در ادامه به معرفی برخی از آنها می پردازیم: 

شعاع دایره: پاره خطی که یک سر آن مرکز دایره و سر دیگر آن نقطه ای روی دایره باشد.

وتر دایره: پاره خطی که دو سر آن روی دایره باشد.

قطر دایره: وتری از دایره که از مرکز دایره می گذرد. 

کمان: کمان دایره شامل دو نقطه روی دایره و تمام نقاط بین آن دو نقطه روی محیط دایره است.

اندازه کمان: همان اندازه زاویه مرکزی مقابل به آن کمان تعریف می شود و واحد آن درجه است.

نکته: نسبت اندازه کمان به 360 برابر است با نسبت طول کمان به محیط دایره. به طور کلی اگر طول کمان را l محیط دایره را P و اندازه کمان را \alpha در نظر بگیریم تساوی زیر همواره برای هر کمان دلخواه برقرار است.

    \[\frac{\alpha}{360}=\frac{l}{P}\]

   

نکته:  اگر اندازه های دو کمان از دایره با هم برابر باشند طول وتر نظیر آنها هم با هم برابر است و بالعکس.

  • کمان های دایره های مختلف می توانند اندازه های برابر و طول های نابرابر داشته باشند.

  •  اگر قطر دایره بر یک وتر عمود باشد پس وتر و کمان متناظر با آن را نصف می کند. و بالعکس اگر قطر دایره یک کمان یا وتر نظیر یک کمان را نصف کرد حتما بر وتر آن عمود است.
  •  اگر وسط یک کمان و وسط وتر نظیرش را به هم وصل کنیم و ادامه دهیم می توانیم قطر عمود بر وتر را رسم کنیم.

با کمک دایره چه زاویه هایی می توانیم داشته باشیم؟

زاویه ها در دایره به سه دسته تقسیم می شوند زاویه مرکزی، زاویه محاطی و زاویه ظلی.

زاویه مرکزی: زاویه ای است که راس آن بر مرکز دایره واقع باشد.

زاویه محاطی: زاویه ای است که راس آن روی دایره و اضلاع آن شامل دو وتر از دایره باشند.

زاویه ظلی: زاویه ای است که در آن راس آن روی محیط دایره و یک ضلع زاویه وتری از دایره و ضلع دیگر مماس بر داره باشند.

تعریف قطاع: ناحیه ای از درون و روی دایره را که به دو شعاع دایره و آن دایره محدود است یک قطاع دایره می نامند. اگر زاویه مرکزی قطاعی از دایره C(O,R) برحسب درجه مساوی \alpha باشد طول کمان AB برابر است با

    \[L=\frac{\pi R}{180}\alpha\]

و مساحت قطاع برابر است با

    \[S=\frac{\pi R^{2}}{360}\alpha\]

 

اندازه ی زاویه مرکزی

زاویه مرکزی

در دایره به زاویه ای که راس آن همان مرکز دایره باشد زاویه مرکزی می گویند. اندازه کمان روبروی زاویه مرکزی دقیقا برابر با اندازه زاویه مرکزی است.

در شکل بالا زاویه AOB یک زاویه مرکزی است که اندازه آن از رابطه زیر بدست می آید:

    \[\alpha=\widehat{AB}\]

 

همانطور که در شکل زیر می بینید اندازه زاویه \alpha دقیقا برابر با کمان روبرویش یعنی کمان AB و کمان CD است. در واقع با اینکه طول دو کمان متفاوت است اما اندازه آنها که برحسب درجه بیان می شود یکسان است. پس می توانیم نکته زیر را داشته باشیم:

نکته: ممکن است دو کمان با اندازه های مساوی، طول های متفاوتی داشته باشند.

دو کمان با اندازه های مساوی می توانند طول های متفاوتی داشته باشند.

زاویه محاطی

اگر در یک دایره راس یک زاویه روی محیط دایره باشد و اضلاع آن زاویه وترهایی از دایره باشند، آنگاه به آن زاویه زاویه محاطی می گویند. اندزاه زاویه محاطی برابر با نصف کمان روبرو اش است.

در شکل زیر زاویه A یک زاویه محاطی است که اندازه آن از رابطه ی زیر بدست می آید:

    \[BAC=\frac{\widehat{BC}}{2}\]

اندازه زاویه محاطی

زاویه ظلی

زاویه ظلی زاویه ای است که راس آن روی دایره قرار دارد و یکی از اضلاع آن مماس بر دایره و ضلع دیگر آن شامل وتری از دایره باشد.

قضیه: اندازه هر زاویه ظلی برابر است با نصف اندازه کمان مقابل به آن زاویه.

در شکل زیر زاویه A یک زاویه ظلی است که اندازه آن از رابطه ی زیر بدست می آید:

    \[BAC=\frac{\widehat{AB}}{2}\]

اندازه زاویه ظلی

نکته: دو وتر که یکدیگر را درون دایره قطع نمی کنند با هم موازی اند اگر و تنها اگر کمان های محدود بین آنها مساوی باشد.

 اندازه زاویه A در شکل زیر برابر است با:

    \[BAC=\frac{DE-BC}{2}\]

اندازه زاویه ای که از برخورد دو وتر در خارج از دایره ایجاد می شود

نکته:  اندازه زاویه A در شکل زیر  برابر است با :

    \[DAE=\frac{DE+BC}{2}\]

اندازه زاویه ای که از برخورد دو وتر دلخواه از دایره ایجاد شده

چطور از یک نقطه خارج از دایره بر آن دایره یک مماس رسم کنیم؟

برای رسم خط مماس بر دایره به مرکز O از نقطه M خارج از دایره، مطابق شکل زیر ابتدا دایره ای به قطر OM رسم می کنیم این دایره، دایره ی اصلی را در دو نقطه قطع می کند این دو نقطه را به نقطه M وصل می کنیم حالا دو خط مماس از نقطه M بر دایره به مرکز O داریم. (چون زاویه محاطی مقابل به قطر، قائمه است)

رسم مماس بر دایره از نقطه ای خارج از دایره

دو دایره چه حالت هایی می توانند نسبت به هم داشته باشند؟

اگر فاصله مرکز دو دایره را d نام گذاری کنیم و شعاع دایره ها را R_{1}\,\,,\,\,R_{2} نام گذاری کنیم می توانیم برای مقادیر مختلف شعاع های دایره و طول خط المرکزین که همان فاصله بین مرکز دو دایره است حالت های زیر را داشته باشیم:

 

دو دایره متخارج

دو دایره بیرون هم (متخارج) هستند اگر رابطه بین خط المرکزین و شعاع دو دایره به صورت

d > R_{1}+R_{2}  باشد. در شکل زیر دو دایره متخارج اند:

دو دایره متخارج و خط المرکزین

هر خط یا پاره خطی که بر هردو دایره مماس باشد، مماس مشترک دو دایره است. اگر دو دایره در یک طرف خط باشند، آن را مماس مشترک خارجی، و اگر دو دایره در دو طرف خط باشند آن را مماس مشترک داخلی می نامند. مثلا در شکل زیر خطوط قرمز مماس مشترک خارجی دو دایره و خطوط آبی مماس مشترک داخلی دو دایره هستند.

دو دایره متخارج و مماس های مشترک شان

اندازه مماس مشترک خارجی با توجه به طول خط المرکزین و اندازه شعاع دو دایره بدست می آید مثلا در شکل زیر اندازه مماس مشترک خارجی برابر است با:

    \[TT^{'}=\sqrt{d^{2}-(R-R^{'})^{2}}\]

اندازه مماس مشترک خارجی دو دایره ی متخارج

اندازه مماس مشترک داخلی با توجه به طول خط المرکزین و اندازه شعاع دو دایره بدست می آید. مثلا در شکل زیر اندازه مماس مشترک داخلی برابر است با:

    \[TT^{'}=\sqrt{d^{2}-(R+R^{'})^{2}}\]

اندازه مماس مشترک داخلی دو دایره متخارج

دو دایره مماس برون

دو دایره مماس برون هستند اگر رابطه بین خط المرکزین و شعاع دو دایره به صورتd=R_{1}+R_{2} باشد. در شکل زیر دو دایره مماس بیرون اند:

دو دایره مماس برون

دو دایره متقاطع

دو دایره متقاطع هستند اگر رابطه بین خط المرکزین و شعاع دو دایره به صورت R_{1}-R_{2} < d < R_{1}+R_{2} باشد. در شکل زیر دو دایره متقاطع اند:

دو دایره متقاطع

دو دایره مماس درون

دو دایره مماس درون هستند اگر رابطه بین خط المرکزین و شعاع دو دایره به صورت d=R_{1}-R_{2} باشد. در شکل زیر دو دایره مماس درون اند:

دو دایره مماس درون

دو دایره متداخل

دو دایره متداخل هستند اگر رابطه بین خط المرکزین و شعاع دو دایره به صورت d < R_{1}-R_{2} باشد. در شکل زیر دو دایره متداخل اند:

دو دایره متداخل

دو دایره هم مرکز

دو دایره هم مرکز هستند اگر رابطه بین خط المرکزین و شعاع دو دایره به صورت  d=0  باشد. در شکل زیر دو دایره هم مرکز را می بینید:

دو دایره هم مرکز

دو دایره را که فقط یک نقطه مشترک داشته باشند، مماس می نامند. در این نقطه مشترک یک خط بر هر دو مماس است. اگر مرکزهای دو دایره در دوطرف این مماس باشند، آن دو دایره، مماس برونی است و اگر هر دو مرکز در یک طرف این مماس باشند، آنها را مماس درونی می نامند.

شکل زیر دو دایره که مماس داخل هستند را نشان می دهد مشاهده می کنید اگر دو دایره مماس داخل باشند فقط یک مماس مشترک دارند. 

دو دایره مماس درون و وتر مشترک شان

شکل زیر دو دایره که مماس برون اند را نشان می دهد همانطور که می بینید اگر دو دایره مماس خارج باشند سه مماس مشترک دارند. و طول خطوط مماس بنفش رنگ برابر است با:

    \[TT^{'}=2\sqrt{RR^{'}}\,\,\,,\,\,\, d=R+R^{'}\]

دو دایره مماس بیرون و وترهای مشترک شان

نکته : دو دایره متقاطع فقط دو مماس مشترک دارند.

نکته : دو دایره متداخل مماس مشترک ندارد.

در دایره چه روابط طولی ای وجود دارد؟

اگر خط های شامل دو وتر از یک دایره، یکدیگر را در درون یا بیرون دایره قطع کنند بین اندازه پاره خط های حاصل روابطی داریم که به بررسی آنها می پردازیم.

قضیه: هرگاه خط های شامل دو وتر دلخواه  AB و CD در نقطه ای مانند M (درون یا بیرون دایره) یکدیگر را قطع کنند آنگاه داریم:

    \[MA.MB=MC.MD\]

 

خطوط شامل وتر های دایره اگر همدیگر را در داخل یا بیرون دایره قطع کنند یک رابطه ی طولی ایجاد می کنند.

قضیه: هرگاه M نقطه ای بیرون دایره باشد و از M مماس و قاطعی نسبت به دایره رسم کنیم مربع اندازه مماس برابر است با حاصل ضرب اندازه های دو قطعه تقاطع. یعنی طول مماس واسطه هندسی بین دو قطعه قاطع است. مثلا در شکل زیر داریم:

    \[MT^{2}=MA.MB\]

اندازه خط مماس بر دابره

چند نکته درباره دایره

چند نکته درباره ی دایره:

  • شعاع دایره در نقطه تماس بر خط مماس عمود است.
  • خطی که از مرکز دایره بر وتر عمود می شود آن وتر را نصف می کند. و برعکس پاره خطی که مرکز دایره را به وسط وتر وصل می کند بر وتر عمود است.
  • اگر در یک دایره اندازه دو وتر با هم برابر باشد حتما اندازه کمان های نظیرشان هم با هم برابر است و برعکس اگر اندازه دو کمان در یک دایره با هم برابر باشد حتما اندازه وتر های نظیرشان با هم برابر است.
  • در یک دایره اگر دو کمان برابر باشند، وتر های نظیر آنها با هم برابرند و اگر دو وتر برابر باشند، کمان های نظیر آنها نیز با هم برابرند.
  • عمودمنصف هر وتر از دایره دلخواه از مرکز آن دایره می گذرد.
  • اگر از هر نقطه خارج دایره دو خط مماس بر دایره رسم کنیم اندازه دو مماس با یکدیگر برابرند.

نکته : هندسه موسوم به “قضیۀ همپیرامونی” می گوید در بین همۀ شکل های هندسی بسته با محیط ثابت، دایره دارای بیشترین مساحت است. این موضوع در طراحی دایره ای شکل قلعه ها اهمیت بسیاری دارد.  

در ادامه چندین رابطه برای زاویه ها در دایره می بینیم:

انئازه زاویه ای که از دو خط مماس بر دایره ایجاد شده

زاویه ای که از برخورد یک مماس و یک وتر دایره بوجود می آید از رابطه ی زیر بدست می آید:

اندازه زاویه ای که از خط مماس بر دایره و وتری از دایره ایجاد شده

کمان های محصور بین دو وتر موازی با هم برابرند.

دو وتر موازی از دایره دو کمان مساوی تولید می کنند.

کمان های محصور بین یک مماس و یک وتر موازی با آن با هم برابرند.

خط مماس بر دایره و وتر موازی با آن دو کمان مساوی تولید می کنند.

چگونه معادله ی یک دایره را بنویسیم؟

معادله دایره را به چند صورت می توان نوشت. معادله دایره می تواند استاندارد یا ضمنی باشد.

معادله استاندارد دایره به مرکز O(\alpha , \beta) و شعاع r  برابر است با:

    \[(x-\alpha)^{2}+(y-\beta)^{2}=r^{2}\]

 

معادله ضمنی دایره به مرکز  O و شعاع r برابر است با:

x^{2}+y^{2}+ax+by+c=0  که مختصات مرکز و اندازه شعاع به ترتیب O(\frac{-a}{2},\frac{-b}{2}) و r=\frac{\sqrt{a^{2}+b^{2}-4c}}{2} هستند.

توجه: به طور کلی معادله x^{2}+y^{2}+ax+by+c=0  اگر و تنها اگر a^{2}+b^{2} > 4c باشد معادله یک دایره را نشان می دهد. اگر   a^{2}+b^{2} < 4c  این معادله هیچ نقطه ای از صفحه را مشخص نمی کند و اگر a^{2}+b^{2} = 4c این معادله یک نقطه به مختصات (\frac{-a}{2},\frac{-b}{2}) را مشخص می کند.

در نتیجه با داشتن مختصات مرکز و طول شعاع دایره، می توان معادلۀ آن را تعیین کرد و برعکس با داشتن معادلۀ دایره می توان مختصات مرکز و طول شعاع آن را به دست آورد.

جمع بندی

در این مقاله به بررسی دایره پرداختیم. اوضاع نقطه و خط را با دایره بررسی کردیم. انواع زاویه ها را در دایره بیان کردیم و نحوه بدست آوردن هر نوع از زاویه را بررسی کردیم. حالت های دو دایره را با هم با رسم شکل و بیان روابط مربوطه بیان کردیم. روابط طولی در دایره را بررسی کردیم و در نهایت معادله دایره را به دو صورت استاندارد و ضمنی آموزش دادیم. لطفا نظرات خود را در مورد مقاله ی دایره در قسمت کامنت ها بیان کنید. 

2 پاسخ

    1. سلامت باشی عزیزم مرسی از توجهت چشم عزیزم در بروزسانی بعدی در صورت امکان جدولی تعبیه می کنیم مربوط به این مقاله

      پاسخ

دیدگاهتان را بنویسید

نشانی ایمیل شما منتشر نخواهد شد. بخش‌های موردنیاز علامت‌گذاری شده‌اند *

آخرین مطالب وبلاگ

دوره ها

دوره جبر معادله تابع فرامث

دسترسی سریع

دوره ها
آموزش های رایگان
درباره فرامث
تماس با فرامث
حریم خصوصی
قوانین سایت

دسترسی سریع

دوره ها
آموزش های رایگان
درباره فرامث
تماس با فرامث
حریم خصوصی
قوانین سایت

مقالات مادر

اعداد
جبر
مثلثات
دیفرانسیل
آمار
احتمال
هندسه
گسسته