همه چیز درباره ی پیوستگی تابع در نقطه، در بازه و تعریف تابع پیوسته
پیوستگی یک تابع در یک نقطه دلخواه پیش زمینه ای برای یادگیری مشتق، کاربرد مشتق در اکسترمم توابع و بهینه سازی است اما نیازمند داشتن اطلاعات کاملی درباره ی حد می باشد. در این مقاله به آموزش همه چیز درباره ی پیوستگی می پردازیم. ابتدا پیوستگی تابع در یک نقطه را بررسی می کنیم. سپس پیوستگی چپ و راست تابع در یک نقطه را آموزش می دهیم. بعد از آن سراغ آموزش پیوستگی تابع در یک بازه می پردازیم. در نهایت بیان می کنیم که ناپیوستگی تابع در یک نقطه در چه مواقعی اتفاق می افتد. در آخر تابع پیوسته را تعریف کردیم.
چه موقع یک تابع در یک نقطه پیوسته است؟
تعریف پیوستگی : گوییم تابع در نقطه
پیوسته است هر گاه:
بنابراین برای پیوسته بودن تابع در نقطه
باید سه شرط زیر برقرار باشند:
- * تابع
در نقطه
تعریف شده باشد.
- * حد تابع
در نقطه
موجود باشد.
- *مقدار حد تابع
در نقطه
با مقدار
برابر باشد.
چه موقع یک تابع در یک نقطه پیوسته نیست؟
هنگامی که تابع در نقطه
پیوسته نیست می گوییم تابع
در نقطه
ناپیوسته است.
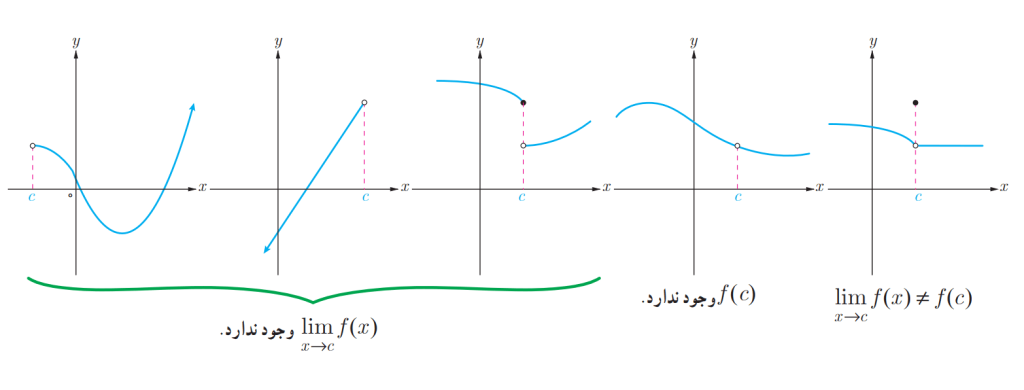
تابع در نقطه
پیوسته نیست اگر یکی از شرایط زیر را داشته باشد:
- *نقطه
در دامنه تابع
نباشد.
- * تابع
در نقطه
تعریف شده باشد ولی در همسایگی اش تعریف نشده باشد.
- * تابع
در نقطه
و همسایگی اش تعریف شده باشد اما تابع
در نقطه
حد نداشته باشد.
- * تابع
در نقطه
و همسایگی اش تعریف شده باشد و تابع
در نقطه
حد داشته باشد اما مقدار حد تابع
در نقطه
با مقدار تابع
در نقطه
برابر نباشد.
پیوستگی چپ و راست یک نقطه چگونه تعریف می شود؟
گوییم تابع در نقطه
از راست پیوسته است (پیوستگی راست دارد) هرگاه:
گوییم تابع در نقطه
از چپ پیوسته است (پیوستگی چپ دارد) هرگاه:
بنابراین هرگاه تابع در یک همسایگی دو طرفه
تعریف شده باشد:
در
پیوسته است اگر و تنها اگر
در
هم از راست و هم از چپ پیوسته باشد.
چه موفع یک تابع در یک بازه پیوسته است؟
تابع را بر بازه باز
پیوسته گوییم هرگاه در هر نقطه
پیوسته باشد.
- تابع
را بر بازه بسته
پیوسته گوییم هرگاه تابع
در هر نقطه
پیوسته باشد و در
از راست پیوسته و در
از چپ پیوسته باشد.
- تابع
را بر بازه باز
پیوسته گوییم هرگاه در هر نقطه
پیوسته باشد.
- تابع
را بر بازه بسته
پیوسته گوییم هرگاه تابع
در هر نقطه
پیوسته باشد و در
پیوسته راست و در
پیوسته چپ باشد.
- تابع
بر بازه
پیوسته است هرگاه تابع
در هر نقطه
پیوسته باشد و در
پیوسته راست باشد.
- اگر تابع
بر بازه
پیوسته باشد و
، یعنی تابع
در
پیوستگی راست دارد و در تمام نقاط بزرگتر از
پیوسته است.
- تابع
را بر بازه
پیوسته گوییم هرگاه تابع
در هر نقطه
پیوسته باشد و در
پیوسته چپ باشد.
- اگر تابع
را بر بازه
پیوسته باشد و
، یعنی تابع
در
پیوستگی چپ دارد و در تمام نقاط کوچکتر از
پیوسته است.
اگر و
در هر نقطه از دامنه اش پیوسته باشد، می گوییم
روی بازه
پیوسته است.
چه موقع یک تابع را پیوسته می نامیم؟
تابعی پیوسته است که در تمام نقاط ورودی شامل اعداد حقیقی، پیوسته باشد. به این معنا که اگر بخواهیم نمودار تابع را رسم کنیم اصلا قلم را از روی کاغذ برنداریم. تابع پیوسته با پیوستگی تابع متفاوت است. پیوستگی تابع برای یک نقطه یا بازه مشابه آنچه در بالاتر آموزش دیدیم تعریف می شود اما وقتی می گوییم یک تابع پیوسته است به این معناست که تابع در همه ی نقاط حقیقی پیوسته است.
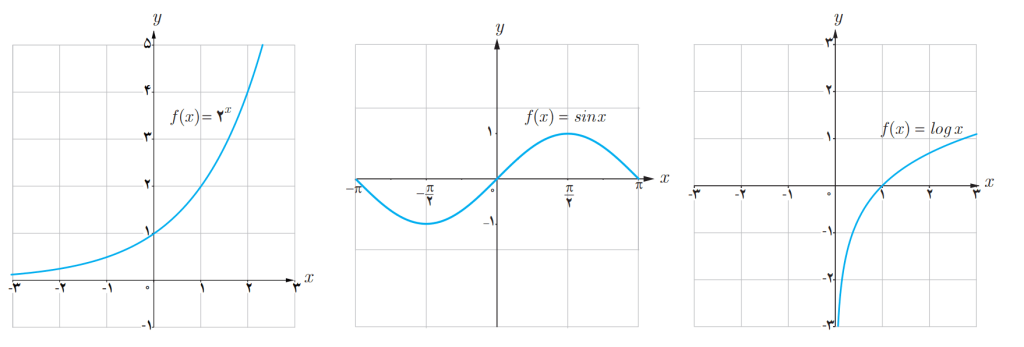
- توابعی مانند سینوس و کسینوس که توابعی مثلثاتی هستند توابعی پیوسته اند. اما تابع تانژانت و کتانژانت توابعی ناپیوسته اند. یعنی برای اینکه نمودار آنها را رسم کنیم باید در برخی نقاط که به ترتیب کسینوس و سینوس را صفر می کنند قلم را از روی کاغذ برداریم.
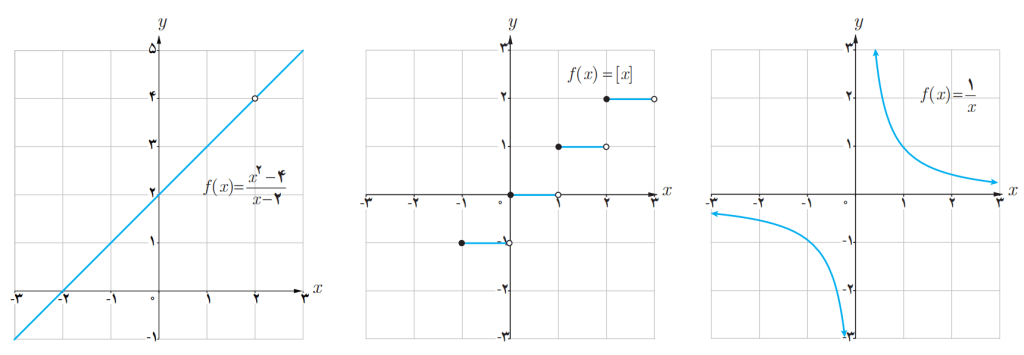
- به طور کلی در توابع گویا به ازای مقادیری که مخرج کسر گویا را صفر می کنند تابع ناپیوسته است. از تعریفی که از توابع ناپیوسته یاد گرفتیم می دانیم که اگر یک نقطه در دامنه تابع نباشد آنگاه تابع در آن نقطه ناپیوسته است. بنابراین توابع گویا در ریشه مخرج ناپیوسته اند.
- می توان گفت توابع گویا تنها در صورتی توابعی پیوسته اند که مخرج آنها ریشه حقیقی نداشته باشد.
- تابع جزصحیح (نمونه ای توابع پلکانی )
یک تابع ناپیوسته است.
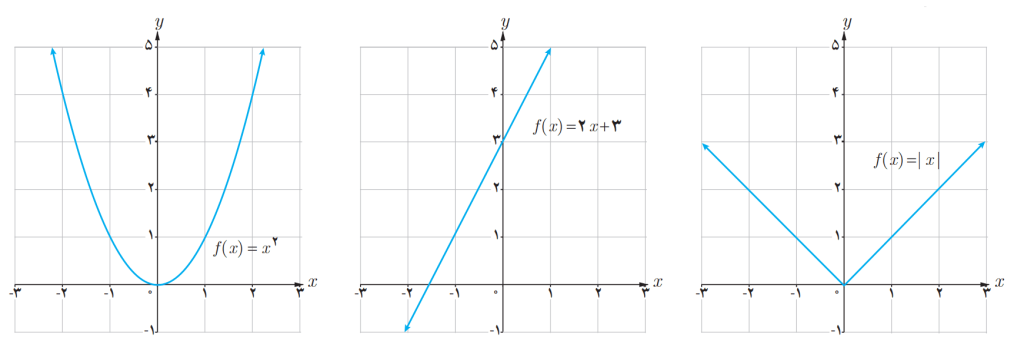
- تابع قدرمطلق
یک تابع پیوسته است.
در حالت کلی برای اینکه بگوییم یک تابع پیوسته است باید بتوانیم پیوستگی آن تابع را در هر نقطه دلخواه تضمین کنیم.
نمودار های زیر توابعی را نشان می دهند که در دامنه شان پیوسته اند:
نمودارهای زیر توابعی را نشان می دهند که در دامنه شان نقطه ناپیوستگی دارند:
جمع بندی
در این مقاله به تعریف پیوستگی تابع در یک نقطه بیان کردیم سپس پیوستگی تابع در یک بازه را بیان کردیم پیوستگی چپ و راست هم در این مقاله بیان شده است. ناپیوستگی یک تابع که به معنای پیوسته نبودن تابع است هم در این مقاله تعریف شده و همه ی شرایط آن آموزش داده شده است. در نهایت بیان کردیم چطور یک تابع پیوسته است و این موضوع با پیوستگی تابع در یک نقطه فرق دارد. برای این که از این آموزش بهره بهتری ببینید حتما قبل از این که این مقاله را بخوانید به مقاله حد و مجانب مراجعه کنید. برای تکمیل کردن اطلاعات خود می توانید به سراغ مقالات مشتق، کاربرد مشتق در یافتن اکسترمم توابع و بهینه سازی بروید. لطفا ما را از نظرات ارزشمند خود در مورد مقاله پیوستگی در قسمت کامنت ها بهره مند کنید.


2 پاسخ
عهههه تازه فهمیدم همش پیوستگی در نقطه رو با پیوستگی بازه اشتباه می گرفتم همه چی درهم میشد
مرسیییی
خوشحالم گره ذهنی ات بازه شده موفق باشی عزیزم