فرامث دات کام
حساب کاربری تو
برای ورود یا ثبت نام بیا اینجا
سبد خریدت اینجاست

آموزش جامعی در باب اینکه مشتق چیست و چگونه می توان مشتق یک تابع را بدست آورد؟

مشتق یک تابع در یک نقطه را می توان شیب خط مماس بر آن تابع در نقطه مورد نظر تعریف کرد. در این مقاله مشتق تابع را با کمک شیب خط تعریف کردیم. سپس مماس بر منحنی را تعریف کرده و شیب خط مماس بر منحنی را تعریف کرده و با توجه به شیب خط مماس بر منحنی مشتق در یک نقطه را تعریف کردیم. سپس فرمول مشتق برخی از توابع را با ذکر مثال هایی بیان کردیم. روابط جبری در توابع و قاعده ی زنجیره ای توابع مرکب را آموزش دادیم. آهنگ متوسط و آهنگ لحظه ای تغییر یک تابع را بیان کردیم. نحوه بدست آوردن مشتق دوم یک تابع را آموزش دادیم. در نهایت با مثال هایی در مورد آهنگ رشد و سرعت متوسط و لحظه ای کاربردهایی از آهنگ متوسط و لحظه ای تغییر یک تابع را آموزش دادیم. اگر به دنبال یک آموزش جامع درباره ی مشتق هستید هرگز این مقاله را از دست ندهید. پیشنهاد می کنیم قبل از خواندن این مقاله پیش زمینه ای از حدو مجانب، پیوستگی، تابع، انواع توابع و مثلثات داشته باشید. با ما در این آموزش همراه باشید.

چگونه با کمک شیب خط مشتق را تعریف کنیم؟

تابع مشتق یک خط در واقع شیب آن خط است. در یک خط شیب آن خط همان مشتق تابع خط است. در معادله خط y=mx+b که می توان آن را به صورت تابع خطی f(x)=mx+b نوشت، شیب خط برابر با m می باشد. چون مشتق براساس شیب خط تعریف می شود بنابراین f^{'}(x)=m می باشد. علامتی که بالای f(x) که خروجی تابع است قرار می دهیم ” پیریم” خوانده می شود. می گوییم ” اِف پیریم برابر است با اِم “.

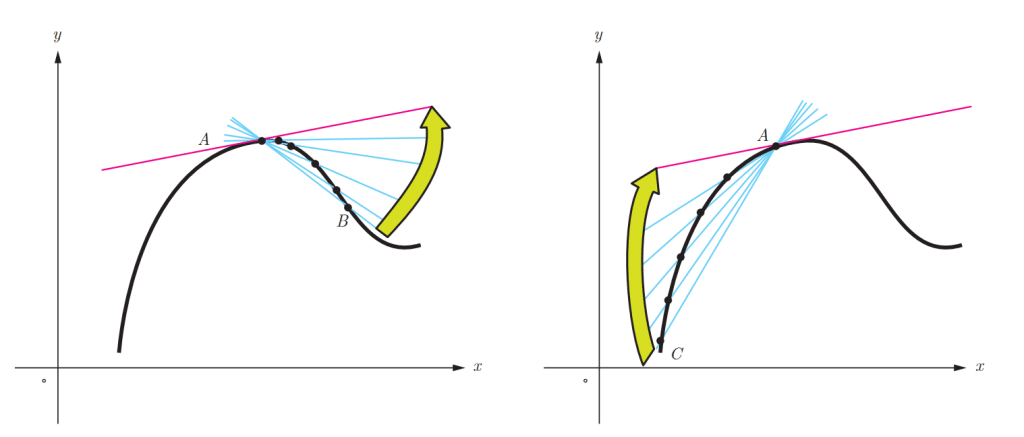
چگونه مشتق منحنی در یک نقطه را بدست آوریم؟

برای اینکه مشتق یک منحنی را در یک نقطه بدست آوریم باید شیب خط مماس بر آن نقطه را بدست آوریم. برای اینکار باید با چند اصطلاح زیر آشنا شویم:

 

تعریف مماس بر منحنی

خط مماس بر دایره، خطی است که با دایره یک و فقط یک نقطه مشترک داشته باشد. این تعریف در حالت کلی برای همه منحنی ها صادق نیست.

شیب خط مماس بر منحنی در نقطه A حد شیبِ خط های قاطع گذرنده از A است به شرطی که نقطه ها به قدر کافی به A نزدیک شوند.

خطوط مماس بر منحنی از سمت چپ و سمت راست یک نقطه روی منحنی

شیب منحنی در نقطه

ابتدا ما شیب خط گذرنده از دو نقطه A(a,f(a)) و B(a+h,f(a+h)) را بدست می آوریم. از تعریف شیب خط می دانیم:

    \[m=\frac{y_{B}-y_{A}}{x_{B}-x_{A}}=\]

    \[\frac{f(a+h)-f(a)}{a+h-a}=\frac{f(a+h)-f(a)}{h}\]

سپس با کمک حد در نظر می گیریم این دو نقطه بسیار به هم نزدیک اند. در نتیجه داریم:

    \[m=\lim_{h \to 0}{\frac{f(a+h)-f(a)}{h}}\]

در نتیجه می توان گفت که شیب خط مماس بر منحنی تابع  f در نقطه A(a,f(a)) را به صورت زیر بدست می آید:

    \[m_{A}=\lim_{h \to 0}{\frac{f(a+h)-f(a)}{h}}\]

به شرط آنکه این حد موجود و متناهی باشد.

حد بالا را در صورت وجود مشتق تابع f در نقطه a می نامند و با f^{'}(a) نمایش می دهند یعنی:

    \[f^{'}(a)=\lim_{h \to 0}{\frac{f(a+h)-f(a)}{h}}\]

می توان مختصات این دو نقطه بسیار نزدیک به هم را به صورت A(a,f(a)) و B(x,f(x)) را در نظر بگیریم. باز هم با توجه به تعریف شیب خط داریم:

    \[m=\frac{y_{B}-y_{A}}{x_{B}-x_{A}}=\frac{f(x)-f(a)}{x-a}\]

در نتیجه تعریف دیگری برای مشتق به صورت زیر بدست می آید:

    \[f^{'}(a)=\lim_{x \to a }{\frac{f(x)-f(a)}{x-a}}\]

که به طور کلی در تعریف مشتق یک تابع در نقطه A(a,f(a)) می توان نوشت:

    \[f^{'}(a)=\lim_{h \to 0}{\frac{f(a+h)-f(a)}{h}}\]

    \[=\lim_{x \to a }{\frac{f(x)-f(a)}{x-a}}\]

رابطه ی مشتق پذیری با پیوستگی چیست؟

قضیه: اگر تابع f در x=a مشتق پذیر باشد آن گاه f در a پیوسته است.

اگر تابع f در x=a پیوسته نباشد آن گاه f در a مشتق پذیر هم نیست.

یادآوری: دو گزاره بالا دو گزاره هم ارزش اند و در اینجا ارزش هر دو درست است چراکه عکس نقیض یکدیگرند.

 

تعریف: مشتق راست و مشتق چپ تابع f در x=a را با f_{+}^{'}(a) و f_{-}^{'}(a) نمایش می دهیم و آن را با کمک حد راست و چپ بصورت زیر تعریف می کنیم:

    \[$f_{+}^{'}(a)$=\lim_{h \to 0^{+}}{\frac{f(a+h)-f(a)}{h}}\]

    \[=\lim_{x \to a^{+}}{\frac{f(x)-f(a)}{x-a}}\]


    \[$f_{-}^{'}(a)$=\lim_{h \to 0^{-}}{\frac{f(a+h)-f(a)}{h}}\]

    \[=\lim_{x \to a^{-}}{\frac{f(x)-f(a)}{x-a}}\]

 

نکته : اگر تابع f در x=a پیوسته باشد و در این نقطه مشتق چپ و راست نامتناهی داشته باشد در این صورت خط  x=a را مماس قائم بر منحنی  f در نقطه (a,f(a)) می نامیم. بدیهی است f^{'}(a) در این حالت وجود ندارد.

چه زمانی یک تابع مشتق پذیر نیست؟

اگر تابع f در x=a هر یک از شرایط زیر را داشته باشد در این صورت در این نقطه مشتق پذیر نیست.

*تابع f در a پیوسته نباشد.

*تابع f در a پیوسته باشد و مشتق راست و مشتق چپ در x=a یکی از سه حالت زیر را داشته باشد:

  • -هر دو موجود و متناهی ولی نابرابر باشند.(نقطه گوشه ای)
  • -یکی متناهی و دیگری نامتناهی باشد (نقطه گوشه ای)
  • -هر دو نامتناهی باشند.

تابع مشتق را چگونه تعریف می کنیم؟

تاکنون با مفهوم مشتق تابع در یک نقطه معین آشنا شده اید. حال به دنبال یافتن رابطه ای بین مجموعه نقاط متعلق به دامنه یک تابع و مشتق تابع در آن نقاط هستیم.

تعریف: اگر x عضوی از دامنه  fباشد تابع مشتق f در x را با f^{'}(x) نمایش می دهیم و آن را به صورت زیر تعریف می کنیم:

    \[f^{'}(x)=\lim_{h \to 0}{\frac{f(x+h)-f(x)}{h}}\]

مشروط بر آنکه حد فوق موجود باشد. مجموعه تمام نقاطی از دامنه  fکه برای آنها  f^{'} موجود باشد را دامنه ی  f^{'}می نامیم.

مشتق توابع ثابت، رادیکالی، خطی، توانی، لگاریتمی، مثلثاتی چگونه بدست می آید؟

در این بخش به بررسی تابع مشتق برخی از انواع تابع می پردازیم:

 

مشتق تابع ثابت

 اگر f(x)=c آن گاه f^{'}(x)=0 به عبارت دیگر مشتق تابع ثابت در هر نقطه برابر صفر است.

مثلا مشتق تابع f(x)=\sqrt{3}  برابر است با f^{'}(x)=0 می باشد.

 

مشتق تابع خطی

مشتق تابع خطی f(x)=ax+b برابر است با f^{'}(x)=a    

مثلا مشتق تابع f(x)=-3x+\frac{2}{7} برابر است با f^{'}(x)=-3.

 

مشتق تابع توانی f(x)=x^{n}\,\,,\,\,n \in \Bbb{R} بصورت f^{'}(x)=nx^{n-1} می باشد.

 

مشتق تابع رادیکالی f(x)=\sqrt{x} و x > 0  بصورت f^{'}(x)=\frac{1}{2\sqrt{x}} می باشد.

نکته: اگر f(x)=\sqrt{ax+b} و ax+b > 0  آنگاه f^{'}(x)=\frac{a}{2\sqrt{ax+b}}.

مثلا اگر f(x)=\sqrt[3]{x}  آنگاه f^{'}(x)=\frac{1}{3\sqrt[3]{x^{2}}} .

مثلا برای بدست آوردن مشتق تابع g(x)=\sqrt[5]{(7x-8)^{2}} ابتدا باید تابع را به صورت یک عبارت توان دار بنویسیم g(x)=\sqrt[5]{(7x-8)^{2}}=(7x-8)^{\frac{2}{5}} حالا با توجه به فرمول f^{'}(x)=nx^{n-1} بعنوان مشتق ِ تابع f(x)=x^{n} می نویسیم:

    \[g^{'}(x)=\frac{2}{5}(7x-8)^{\frac{2}{5}-1}(7x-8)^{'}\]

    \[=\frac{2}{5}(7x-8)^{\frac{-3}{5}}(7)=\frac{14}{5\sqrt[5]{(7x-8)^{3}}}\]

 

مشتق تابع نمایی f(x)=a^{x} برابر با f^{'}(x)=a^{x}\ln{a} می باشد.

مثال: مشتق تابع f(x)=7^{x}  برابر است با f^{'}(x)=7^{x} \ln{7}  

مشتق تابع لگاریتمی f(x)=\log_{a}{x} برابر با f^{'}(x)=\frac{1}{x\ln{a}} می باشد.

مثال: مشتق تابع f(x)=\log_{8}{x} برابر است با f^{'}(x)=\frac{1}{x\ln{8}} 

 

مشتق توابع مثلثاتی

مشتق تابع مثلثاتی سینوسf(x)=\sin{x} برابر است با f^{'}(x)=\cos{x}  

مشتق تابع مثلثاتی کسینوس f(x)=\cos{x} برابر است با f^{'}(x)=-\sin{x}  

مشتق تابع مثلثاتی تانژانت f(x)=\tan{x} برابر است با f^{'}(x)=1+\tan^{2}{x}  

مشتق تابع مثلثاتی کتانژانت f(x)=\cot{x} برابر است با f^{'}(x)=-(1+\cot^{2}{x})  

روابط جبری در مشتق توابع

اگر توابع f و g در x=a مشتق پذیر باشند آنگاه توابع kf ،f \pm g ،fg و \frac{f}{g}\, , \,\, g(a) \neq 0 نیز در x=a مشتق پذیرند و داریم:

    \[(f \pm g)^{'}(a)=f^{'}(a)\pm g^{'}(a)\]

    \[(kf)^{'}(a)=kf^{'}(a)\]

    \[(fg)^{'}(a)=f^{'}(a)g(a)+f(a)g^{'}(a)\]

    \[(\frac{f}{g})^{'}(a)=\frac{f^{'}(a)g(a)-f(a)g^{'}(a)}{(g(a))^{2}}\]

مثال: مشتق تابع f(x)=(\sin{x}+\cos{x})\tan{x} را بدست آورید؟

ابتدا به این توجه می کنیم که تابع f(x) حاصل ضرب دو تابع (\sin{x}+\cos{x}) و \tan{x} می باشد. بنابراین مشتق آن برابر است با مجموع مشتق یکی در دیگر و بالعکس آن. بنابراین داریم:

    \[f^{'}(x)=(\sin{x}+\cos{x})^{'}\tan{x}\]

    \[+(\sin{x}+\cos{x})(\tan{x})^{'}\]


    \[=(\cos{x}-\sin{x})\tan{x}\]

    \[+(\sin{x}+\cos{x})(1+\tan^{2}{x})\]

مشتق توابع مرکب: قاعده ی زنجیره ای

اگر  f و g دو تابع مشتق پذیر باشند در این صورت تابع مرکب fog مشتق پذیر است و داریم:

    \[(fog)^{'}(x)=g^{'}(x)f^{'}(g(x))\]

اگر  f تابعی برحسب  u و u تابعی از x باشد:

    \[y=f(u) \,\,\,,\,\,\, y^{'}=u^{'}f^{'}(u)\]

 

مثال: مشتق تابع h(x)=a^{\sin{x}} را بدست آورید.

برای حل این سوال ابتدا در نظر می گیریم f(x)=a^{x} و g(x)=\sin{x} حالا می توانیم سوال را به صورت زیر بازنویسی کنیم: h(x)=f(g(x)) بنابراین می توانیم مشتق تابع h(x)  را بدست آوریم:

    \[h^{'}(x)=g^{'}(x)f^{'}(g(x))=\cos{x} \, a^{\sin{x}}\ln{a}\]

مشتق پذیری روی یک بازه چگونه تعریف می شود؟

تابع f روی بازه ی (a,b) مشتق پذیر است هرگاه، در هر نقطه این بازه مشتق پذیر باشد.

تابع f روی بازه ی [a,b]   مشتق پذیر است هرگاه f در بازه ی (a,b) مشتق پذیر باشد و در نقطه a مشتق راست و در  b مشتق چپ داشته باشد.

مشتق مرتبه دوم یک تابع چگونه بدست می آید؟

برای محاسبه مشتق دوم از مشتق اول ِ تابع یک بار دیگر مشتق می گیریم.

مثال: مشتق دوم تابع g(x)=\sin{x} را بدست آورید.

    \[g^{``}=(\sin{x})^{``}=(\cos{x})^{'}=-\sin{x}\]

آهنگ متوسط تغییر و آهنگ لحظه ای تغییر چگونه تعریف می شود؟

به طور کلی آهنگ متوسط تغییر یک تابع در بازه [a,a+h] به شکل زیر تعریف می شود:

    \[\frac{f(a+h)-f(a)}{h}\]

آهنگ متوسط تغییر در بازه [a,a+h] با شیب خط قاطع ِ دو سر بازه با هم برابرند.

همچنین آهنگ تغییر لحظه ای تابع f در نقطه x=a بصورت زیر تعریف می شود:

    \[\lim_{h \to 0}{\frac{f(a+h)-f(a)}{h}}=f^{'}(a)\]

آهنگ لحظه ای تابع در یک نقطه با مقدار مشتق و شیب خط مماس در آن نقطه برابرند.

مثال: در تابع f(x)=x^{2}+5x-7  

الف) آهنگ متوسط تابع در بازه [1,3]  را بدست آورید.

ب) آهنگ لحظه ای تابع در نقطه x=-1  بدست آورید.

ج) شیب خط مماس بر تابع در نقطهx=0  را بدست آورید.

جواب:

الف) برای بدست آوردن آهنگ متوسط تابع در بازه [1,3]  باید از فرمول شیب خط که در قسمت های قبل به آن اشاره شده بود استفاده کنیم در نتیجه داریم:

    \[\frac{f(3)-f(1)}{3-1}=\]

    \[\frac{(9+15-7)-(1+5-7)}{2}\]

    \[=\frac{17-(-1)}{2}=\frac{18}{2}=9\]

ب) برای بدست آوردن آهنگ لحظه ای تابع در نقطه x=-1 باید مشتق تابع در این نقطه را بدست آوریم. بنابراین ابتدا مشتق تابع را با کمک فرمول هایی که در بالاتر گفته شد بدست می آوریم:

    \[f^{'}(x)=2x+5\]

حالا کافی است مقدار تابع را به ازای نقطه مورد نظر بدست آوریم:

    \[f^{'}(-1)=2x+5=-2+5=3\]

ج) برای بدست آوردن شیب خط مماس بر تابع در نقطه x=0  باید مشتق تابع در این نقطه را بدست آوریم. بنابراین ابتدا مشتق تابع را با کمک فرمول هایی که در بالاتر گفته شد بدست می آوریم:

    \[f^{'}(x)=2x+5\]

حالا کافی است مقدار تابع را به ازای نقطه مورد نظر بدست آوریم:

    \[f^{'}(0)=2x+5=0+5=5\]

کاربردهایی از آهنگ متوسط تغییر تابع و آهنگ لحظه ای یک تابع

در این بخش از مقاله آهنگ متوسط و لحظه ای را از دید مفهوم سرعت و آهنگ رشد بررسی می کنیم. هر مورد را در ادامه می بینید.

 

سرعت متوسط و سرعت لحظه ای

سرعت متوسط یک متحرک برابر است با میزان جابجایی متحرک تقسیم بر مدت زمان جابجایی متحرک. سرعت لحظه ای یک متحرک، سرعت آن متحرک در لحظه ی مورد نظر است.

برای بدست آوردن سرعت متوسط و سرعت لحظه ای به ترتیب می توانیم از آهنگ تغییر متوسط تابع و آهنگ تغییر لحظه ای تابع که همان مشتق تابع است استفاده کنیم.

برای یادگیری بهتر و فهمِ این موضوع به مثال ساده ی زیر توجه کنید:

خودرویی در امتداد خط راست طبق معادله d(t)=-5t^{2}+20t حرکت می کند، که در آن 0 \le t \le 5 بر حسب ثانیه است. الف) سرعت متوسط خودرو را در بازه زمانی [1,2] بدست آورید. ب) سرعت لحظه ای خودرو را در زمان های t=1 و t=2 و t=3 بدست آورید.

جواب:

الف) برای بدست آوردن سرعت متوسط خودرو در بازه زمانی [1,2] باید از فرمول شیب خط که در قسمت های قبل به آن اشاره شده بود استفاده کنیم در نتیجه داریم:

    \[\frac{d(2)-d(1)}{2-1}=\]

    \[\frac{(-20+40)-(-5+20)}{1}=\]

    \[\frac{20-15}{1}=\frac{5}{1}=5\]

ب) برای بدست آوردن سرعت لحظه ای خودرو را در زمان هایt=1 و t=2 و t=3 باید مشتق تابع در این نقاط بدست آوریم. بنابراین ابتدا مشتق تابع را با کمک فرمول هایی که در بالاتر گفته شد بدست می آوریم:

    \[d^{'}(t)=-10t+20\]

حالا کافی است مقدار مشتق تابع را به ازای نقاط مورد نظر بدست آوریم:

    \[d^{'}(1)=-10+20=10\]

    \[d^{'}(2)=-20+20=0\]

    \[d^{'}(3)=-30+20=-10\]

سرعت صفر یعنی خودرو در آن لحظه یعنی لحظه t=2 ساکن است.

سرعت منفی یعنی خودرو در آن لحظه در خلاف جهت مورد نظر حرکت می کند. (جهت ها در فیزیک قراردادی اند. کسی که معادله حرکت خودرو را نوشته یک جهت مثبت را برای حرکت در نظر گرفته و براساس آن معادله را نوشته است. وقتی سرعت خودرو مثبت است یعنی در همان جهتی که طراح سوال مثبت درنظر گرفته حرکت می کند. اگر سرعت منفی شود یعنی در خلاف جهتی که طراح سوال در نظر گرفته حرکت می کند.)

نکته دیگر اینکه همانطور که در مورد سهمی قائم خواندیم می دانیم در راس سهمی شیب خط مماس صفر است. همانطور که در مورد معادله خط خواندیم می دانیم که وقتی شیب خط صفر باشد خط به صورت افقی هست. بنابراین می توان گفت در معادله جابجایی درجه دویی که سوال به ما داده است. یک سهمی داریم که راس آن در t=2 قرار دارد و خط مماس بر منحنی در این نقطه یک خط افقی است که شیب آن صفر است. همچنین از آنجا که ضریب  t^{2} یک عدد منفی است پس سهمی رو به پایین است و شیب خطوط مماس بر منحنی در  tهای کوچکتر از  2 مثبت و در  tهای بزرگتر از 2 منفی است.

 

 

آهنگ رشد

آهنگ رشد قد کودکان برحسب سانتی متر تا حدود 60 ماهگی را می توان با تابع f(x)=7\sqrt{x}+50 نشان داد که در آن x مدت زمان پس از تولد برحسب ماه است. آهنگ متوسط رشد در بازه زمانی  [0,60] به صورت زیر بدست می آید:

    \[\frac{f(60)-f(0)}{60-0}=\]

    \[\frac{(7\sqrt{60}+50)-(7\sqrt{0}+50)}{60}\]

    \[=\frac{7\sqrt{60}}{60}\cong 0.9\]

 یعنی در طی این 5 سال رشد متوسط قد حدود 0.9 سانتی متر در هر ما است.

آهنگ متوسط رشد در بازه زمانی [0,25] به صورت زیر بدست می آید:

    \[\frac{f(25)-f(0)}{25-0}=\]

    \[\frac{(7\sqrt{25}+50)-(7\sqrt{0}+50)}{25}=\]

    \[\frac{85-50}{25}=\frac{35}{25}=1.4\]

آهنگ لحظه ای تغییر قد کودک در 25 ماهگی و 49 ماهگی را با هم مقایسه کنید کدامیک بیشتر است؟

برای بدست آوردن آهنگ لحظه ای تابع در نقاط موردنظر باید مشتق تابع را در این نقاط بدست آوریم. بنابراین ابتدا مشتق تابع را با کمک فرمول هایی که در بالاتر گفته شد بدست می آوریم:

    \[f(x)=7\sqrt{x}+50\,\,\,\rightarrow \,\,\,f^{'}(x)=\frac{7}{2\sqrt{x}}\]

حالا کافی است مقدار مشتق تابع را به ازای نقاط مورد نظر بدست آوریم:

    \[f^{'}(25)=\frac{7}{2\sqrt{25}}=0.7\]

    \[f^{'}(49)=\frac{7}{2\sqrt{49}}=0.5\]

می بینیم آهنگ رشد لحظه ای در 25 ماهگی بیشتر از 49 ماهگی است. بچه ها هرچه کوچکترند سرعت رشدشان بیشتر است.

اگر قد علی در 16 ماهگی ، 80 سانتی متر و در 36 ماهگی، 95 سانتی متر باشد، آهنگ متوسط تغییر رشد او را در این فاصله حساب کنید.

    \[\frac{f(36)-f(16)}{36-16}=\frac{95-80}{20}=\frac{15}{20}=0.75\]

اگر بخواهیم آهنگ متوسط رشد علی را با تابع رشد کودکان مقایسه کنیم باید ببینیم به طور کلی کودکان در از 16 تا 36 ماهگی آهنگ متوسط رشدشان چقدر است. داریم:

    \[\frac{f(36)-f(16)}{36-16}=\]

    \[\frac{(7\sqrt{36}+50)-(7\sqrt{16}+50)}{20}=\]

    \[\frac{92-78}{20}=\frac{14}{20}=0.7\]

متوجه می شویم آهنگ رشد علی از سایر کودکان در این بازه زمانی بیشتر است.

 

 

به پایان این مقاله رسیدیم بعنوان برگه فرمول و خلاصه نکات همه ی فرمول ها و نکات مشتق را در جدول های زیر آماده کردیم:

همه ی فرمول های مشتق

جمع بندی

در این مقاله به آموزش مشتق پرداختیم به گونه ای که ابتدا ارتباط آن با شیب خط را بیان کردیم سپس مفهوم شیب خط مماس بر منحنی و ارتباط آن با مشتق منحنی را بیان کردیم. مشتق پذیری و شروط مشتق داشتن یک تابع با توجه به پیوستگی آن تابع را بیان کردیم. نحوه محاسبه مشتق برخی از انواع توابع مانند تابع ثابت، تابع خطی، توابع توان دار و رادیکالی، توابع نمایی و لگاریتمی و توابع مثلثاتی را بیان کردیم. مشتق را وقتی اعمال جبری روی توابع انجام شد بیان کردیم. همچنین به بیان قاعده ای زنجیره ای که قانونی است برای یافتن مشتق ترکیب توابع را بیان کردیم. مشتق مرتبه دوم و نحوه بدست آوردن آن را نشان دادیم. آهنگ متوسط تغییر و آهنگ لحظه ای تغییر یک تابع را آموزش دادیم و کاربردهایی از آن را در بدست آوردن سرعت متوسط و سرعت لحظه ای و همچنین آهنگ رشد کودکان بیان کردیم. اگر علاقمند به دانستن چیزهای بیشتری درباره ی مشتق و کاربرد آن در بدست آوردن اکسترمم یک تابع و بهینه سازی توابع با کمک مشتق هستید لطفا به مقاله کاربرد مشتق در اکسترمم توابع و بهینه سازی مراجعه کنید. لطفا ما را از نظرات خود درباره ی مقاله مشتق در قسمت کامنت ها بهره مند کنید.

 

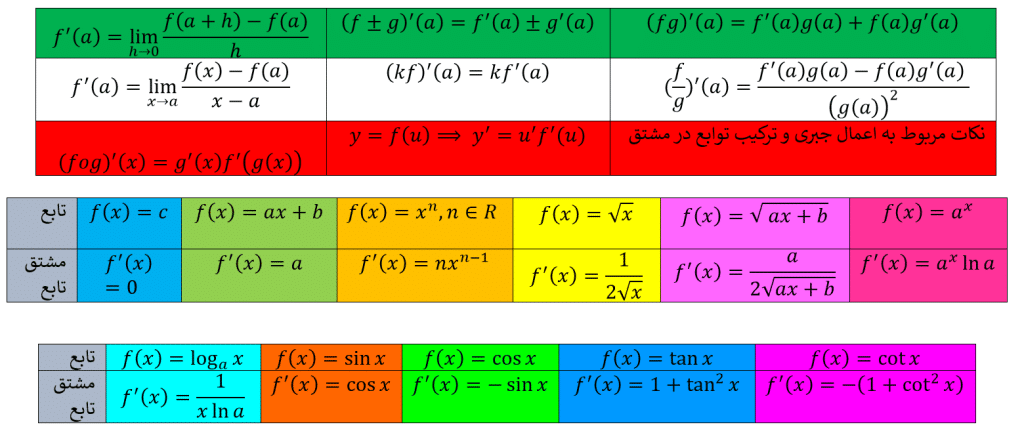
2 پاسخ

  1. عاشق این جدول های آخر مقالات تونم عجب برگه فرمول های خوش رنگ و کاملی😁😇🙏🌺

    پاسخ

دیدگاهتان را بنویسید

نشانی ایمیل شما منتشر نخواهد شد. بخش‌های موردنیاز علامت‌گذاری شده‌اند *

آخرین مطالب وبلاگ

دوره ها

دوره جبر معادله تابع فرامث

دسترسی سریع

دوره ها
آموزش های رایگان
درباره فرامث
تماس با فرامث
حریم خصوصی
قوانین سایت

دسترسی سریع

دوره ها
آموزش های رایگان
درباره فرامث
تماس با فرامث
حریم خصوصی
قوانین سایت

مقالات مادر

اعداد
جبر
مثلثات
دیفرانسیل
آمار
احتمال
هندسه
گسسته