کاربرد مشتق در بهینه سازی و بدست آوردن اکسترمم توابع، نقاط بحرانی و رسم توابع

کاربرد مشتق در بهینه سازی و بدست آوردن اکسترمم و رسم توابع در این مقاله آموزش داده می شود. ولی قبل از اینکه به این موضوع بپردازیم شما نیاز به دانستن همه چیز در مورد مشتق دارید. بنابراین اگر لازم می دانید به مقاله مشتق مراجعه کنید. در ضمن برای اینکه کاربرد مشتق در تشخیص صعودی یا نزولی بودن یک تابع یا همان آزمون یکنوایی، فهمیدن جهت تقعر یک تابع و بدست آوردن نقطه عطف یک تابع، رسم نمودار توابع و بهینه سازی توابع دارید هرگز این مقاله را از دست ندهید. چرا که علاوه بر آموزش جامع و جمع و جور این مطالب، در این مقاله به آموزش پیش نیازهای آنها یعنی اکسترمم نسبی، اکسترمم های مطلق، نقطه بحرانی و آزمون مشتق اول نیز می پردازیم. اگر علاقمند به دانستن همه چیز راجع به کاربرد مشتق هستید اگر می خواهید برای کنکور آماده شوید و نیاز به آموزش جمع و جوری درباره کاربرد مشتق دارید که خیالتان را از دانستن همه ی سرفصل های کاربرد مشتق راحت کند این مقاله همان چیزی است که نیاز دارید.

چگونه اکسترمم نسبی یک تابع را بدست آوریم؟

اگر $f$ یک تابع و $I \subseteq D_{f}$ یک همسایگی از نقطه $c$ (بازه ی باز شامل نقطه $c$ ) باشد که:

*به ازای هر $x$ متعلق به $I$ داشته باشیم $f(x) \le f(c )$ . در این صورت $f(c )$ را یک ماکزیمم نسبی تابع $f$ می نامیم.

*به ازای هر $x$ متعلق به $I$ داشته باشیم $f(x) \ge f(c )$ ، در این صورت $f(c )$ را یک مینیمم نسبی تابع $f$ می نامیم.

تذکر : گوییم تابع $f$ در $x=c$ اکسترمم نسبی دارد هرگاه تابع در این نقطه ماکزیمم نسبی یا مینیمم نسبی داشته باشد.

چگونه نقطه بحرانی یک تابع را بدست آوریم؟

برای تعریف نقطه بحرانی می گوییم نقطه به طول $c$ را یک نقطه بحرانی برای تابع $f$ می نامیم که $c \in D_{f}$ هرگاه $f^{'}(c )$ برابر صفر یا $f^{'}(c )$ ناموجود باشد.

قضیه: اگر تابع $f$ در نقطه به طول $c$ ماکزیمم یا مینیمم نسبی داشته باشد و $f^{'}(c )$ موجود باشد، آنگاه $f^{'}(c )=0$ . به عبارت دیگر، هر نقطه اکسترمم نسبی تابع، یک نقطه بحرانی آن است.

آزموش مشتق اول: تشخیص ماکزیمم نسبی یا مینیمم نسبی بودن یک نقطه بحرانی

فرض کنیم تابع $f$ بر بازه ای باز مانند $I (I \subseteq D_{f}$ پیوسته باشد و $c \in I$ یک نقطه بحرانی تابع $f$ باشد. هرگاه $f$ بر این بازه به جز احتمالا در نقطه $c$ مشتق پذیر باشد در این صورت:

*اگر به ازای تمام مقادیر $x$ در بازه ای مانند $(a,c)$ ، $f^{'}(x) > 0$ و به ازای تمام مقادیر $x$ در بازه ای مانند $(c,b)$ ، $f^{'}(x) < 0$ در این صورت $f(c )$ یک مقدار ماکزیمم نسبی $f$ است.

*اگر به ازای تمام مقادیر $x$ در بازه ای مانند $(a,c)$ ، $f^{'}(x) < 0$ و به ازای تمام مقادیر $x$ در بازه ای مانند $(c,b)$ ، $f^{'}(x) > 0$ در این صورت $f(c )$ یک مقدار مینیمم نسبی $f$ است.

*اگر $f^{'}$ در نقطه $c$ تغییر علامت ندهد به طوری که $f^{'}$ در هر دو طرف $c$ مثبت یا هر دو طرف آن منفی باشد، آنگاه $f(c )$ نه مینیمم و نه ماکزیمم نسبی است.

چطور اکسترمم مطلق یک تابع را بدست آوریم؟

*به بزگترین مقدار تابع در یک بازه، ماکزیمم مطلق ِ تابع در این بازه می گویند. (بالاترین نقطه نمودارتابع)

*به کوچکترین مقدار تابع در یک بازه، مینیمم مطلقِ تابع در این بازه می گویند. (پایین ترین نقطه نمودارتابع)

وقتی می گوییم تابع $f$ در $a$ مینیمم مطلق دارد یعنی $f(a)$ مقدار مینیمم مطلق تابع و $(a,f(a))$ نقطه مینیمم مطلق است.

تذکر: اگر تابع $f$ در $x=c$ ماکزیمم مطلق یا مینیمم مطلق داشته باشد می گوییم در آن نقطه اکسترمم مطلق دارد.

قضیه: اگر تابع $f$ در بازه ی بسته $[a,b]$ پیوسته باشد آن گاه تابع در این بازه هم ماکزیمم مطلق و هم مینیمم مطلق دارد.

تعریف: با فرض $c \subseteq D_{f}$ ، نقطه $(c,f(c ))$ ، یک نقطه ماکزیمم مطلق برای تابع $f$ نامیده می شود، هرگاه به ازای هر $x$ از $D_{f}$ داشته باشیم $f(c ) \ge f(x)$ . در این حالت عدد $f(c )$ را مقدار ماکزیمم مطلق $f$ روی $D_{f}$ می نامیم.

تعریف: با فرض $c \subseteq D_{f}$ ، نقطه $(c,f(c ))$ ، یک نقطه مینیمم مطلق برای تابع $f$ نامیده می شود، هرگاه به ازای هر $x$ از $D_{f}$ داشته باشیم $f(c ) \le f(x)$ . در این حالت عدد $f(c )$ را مقدار مینیمم مطلق $f$ روی $D_{f}$ می نامیم.

قضیه: فرض کنیم تابع $f$ در بازه بسته $[a,b]$ پیوسته باشد. در این صورت $f$ در این بازه هم ماکزیمم مطلق دارد و هم مینیمم مطلق.

مراحل یافتن اکسترمم مطلق تابع پیوسته $f$ در بازه بسته $[a,b]$ به شرح زیر است:

1-مشتق تابع را بدست آورده و نقاط بحرانی $f$ را می یابیم.

2-مقدار تابع را در هر یک از نقاط بحرانی و همچنین در نقاط انتهایی بازه محاسبه می کنیم.

3-در مرحله 2 ، بزرگترین عدد بدست آمده، مقدار ماکزیمم مطلق تابع و کوچکترین آنها مینیمم مطلق تابع در بازه $[a,b]$ است.

آزمون یکنوایی تابع: تشخیص صعودی یا نزولی بودن یک تابع

قضیه : فرض کنیم تابع $f$ بر بازه $[a,b]$ پیوسته و بر بازه $(a,b)$ مشتق پذیر باشد. در این صورت:

*اگر به ازای هر $x$ در بازه $(a,b)$ ، $f^{'}(x) > 0$ ، آن گاه تابع $f$ بر $]a,b]$ صعودی اکید است.

*اگر به ازای هر $x$ در بازه $(a,b)$ ، $f^{'}(x) < 0$ ، آن گاه تابع $f$ بر $[a,b]$ نزولی اکید است.

*اگر به ازای هر $x$ در بازه $(a,b)$ ، $f^{'}(x)=0$ ، آن گاه تابع $f$ بر $[a,b]$ یک تابع ثابت است.

چطور جهت تقعر یک تابع و نقطه عطف آن را بدست آوریم؟

در یک منحنی در هر قسمت که خطوط مماس بر منحنی زیر منحنی بودند تقعر منحنی رو بالاست. و در هر قسمت که خطوط مماس بر منحنی بالای منحنی باشند تقعر رو به پایین است.

قضیه : فرض کنیم $f^{``}(x)$ به ازای هر نقطه $x$ از بازه باز $I$ موجود باشد.

*اگر به ازای هر $x$ از $I$ ، $f^{``}(x) > 0$ آنگاه نمودار $f$ روی بازه $I$ تقعر رو به بالا دارد.

*اگر به ازای هر $x$ از $I$ ، $f^{``}(x) < 0$ آنگاه نمودار $f$ روی بازه $I$ تقعر رو به پایین دارد.

*اگر به ازای هر $x$ از $I$ ، $f^{``}(x)=0$ آنگاه آزمون بی نتیجه است.

تعریف : فرض کنیم تابع $f$ در نقطه $x=c$ پیوسته است. در این صورت نقطه $(c,f(c ))$ نقطه عطف تابع $f$ است هرگاه دو شرط زیر برقرار باشند:

*نمودار $f$ در نقطه $(c,f(c ))$ خط مماس داشته باشد.

*جهت تقعر $f$ در نقطه $(c,f(c ))$ تغییر کند.

برای بدست آوردن نقطه عطف کافی است قرار دهید $f^{``}(x)=0$ و بررسی کنید کدام ریشه های این معادله هر دو شرط نقطه عطف بودن را دارد.

چطور با توجه به مشتق و کاربرد مشتق یک تابع را رسم کنیم؟

برای رسم نمودار یک تابع مراحل زیر را انجام می دهیم:

*دامنه ی تابع را مشخص می کنیم.
*محل تلاقی نمودار با محورهای مختصات را مشخص می کنیم (در صورت وجود)
* $f^{'}$ را به دست می آوریم و با تعیین علامت آن بازه هایی که $f$ بر آنها صعودی یا نزولی است را مشخص می کنیم.
*نقاط بحرانی و اکسترمم های نسبی تابع را به دست می آوریم (در صورت وجود)
* $f^{``}$ را به دست می آوریم و با تعیین علامت آن جهت تقعر تابع در بازه های مختلف را مشخص می کنیم.
*نقطه عطف تابع را مشخص می کنیم. (در صورت وجود)
*رفتار تابع را برای مقادیر بسیار بزرگ $x$ و بسیار کوچک $x$ مشخص می کنیم (در صورت وجود)
*معادله مجانب های تابع را به دست می آوریم (در صورت وجود)
*تنظیم یک جدول که با خلاصه کردن اطلاعات توابع $f$ و $f^{'}$ و $f^{``}$ در آن تشخیص چگونگی شکل نمودار آسان تر شود.
*رسم نمودار تابع با استفاده از اطلاعات قسمت های قبل.
*در صورت نیاز از نقاط کمکی هم استفاده می کنیم.

بهینه سازی: چطور با کمک کاربرد مشتق بهینه ترین حالت یک تابع را بدست آوریم؟

بهینه سازی مسائلی را با هدف ماکزیمم کردن مساحت، حجم، سود یا مینیمم کردن فاصله، زمان و هزینه حل می کند.

برای حل سوالات بهینه سازی ابتدا با کمک اطلاعات مسئله همه ی متغیرها را براساس یک متغیر می نویسیم و در گام بعد با توجه به آنچه در مورد اکسترمم ها آموختیم به حل مسئله می پردازیم و می گوییم به ازای چه مقداری از متغیر، ماکزیمم و یا مینیمم ِ خواسته ی مسئله اتفاق می افتد.

مثال: در بین تمام مستطیل های با محیط ثابت 14 سانتی متر، کدام مستطیل بیشترین مساحت را دارد؟

جواب: یک مستطیل به طول $l$ و عرض $x$ را در نظر میگیریم. می دانیم که محیط و مساحت مستطیل به صورت زیر بدست می آید:

$P=2(x+l) \,\,\,\,,\,\,\,\, S=xl$

که در این سوال آورده شده $P=14$ بنابراین می توان گفت:

$2(x+l)=14 \rightarrow x+l=7 \rightarrow l=7-x$

در نتیجه می توانیم مساحت را بصورت زیر بازنویسی کنیم:

$S=xl=x(7-x)=-x^{2}+7x$

حالا برای اینکه مساحت ماکزیمم شود از مطالبی که در مورد اکسترمم نسبی که در بالاتر آموختیم استفاده می کنیم. یعنی از رابطه ی بدست آمده برای مساحت مشتق می گیریم تا نقطه بحرانی آن را بدست آوریم:

$S^{'}=-2x+7\rightarrow -2x+7=0\rightarrow x=3.5$

برای اینکه حل سوال کامل و دقیق انجام شود باید به این توجه کنیم که طول نمی تواند منفی باشد. پس داریم:

$x,l \ge 0\,\,\,\rightarrow \,\,\, 7-x \ge 0$

$\rightarrow x \le 7\rightarrow 0 \le x پle 7$

بنابراین با توجه به آنچه درباره نقطه بحرانی خواندیم نقاط بحرانی تابع مساحت عبارتند از

$x=0\,\,\,,\,\,\, x=3.5\,\,\,,\,\,\, x=7$

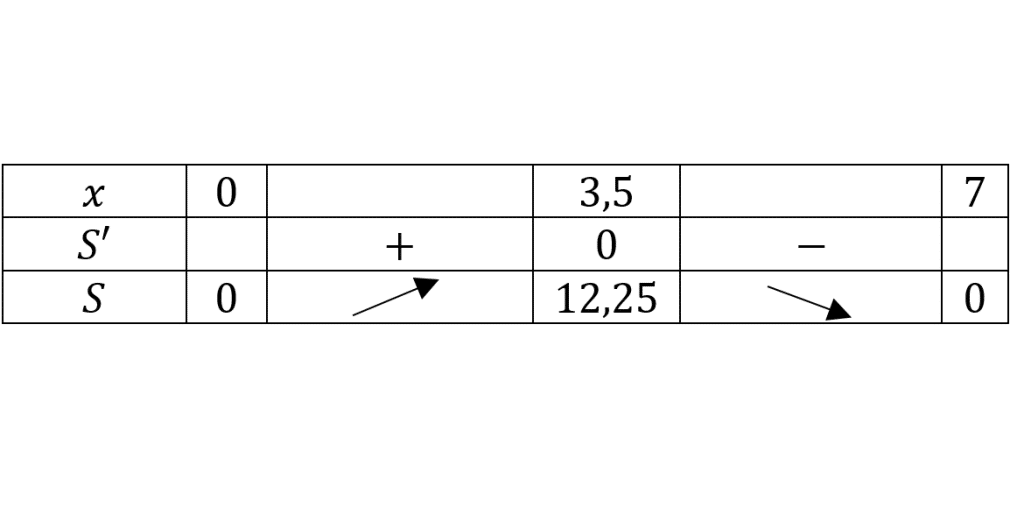
در مرحله بعد باید جدول آزمون مشتق اول را با توجه به نقاط بحرانی رسم کنیم.

با توجه به جدول بالا می بینیم که ماکزیمم مساحت برابر 12.25 است و در $x=3.5$ اتفاق می افتد.

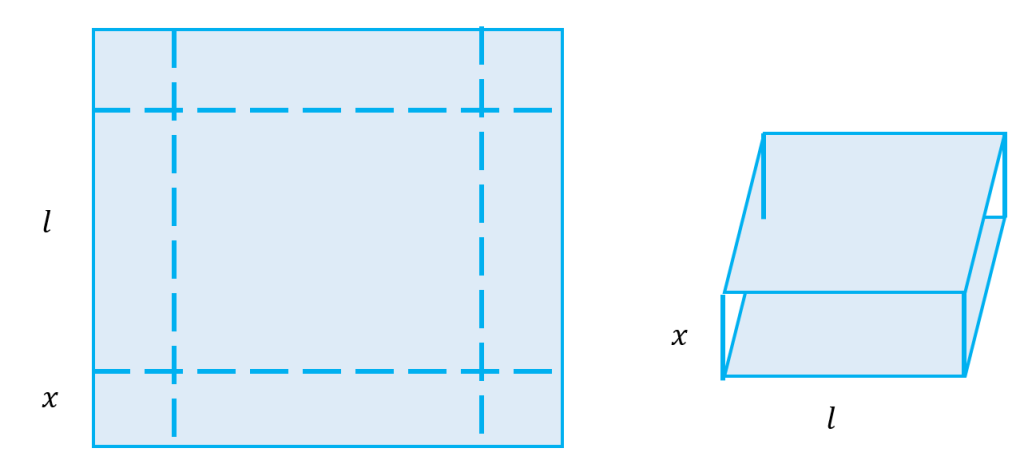
مثال: ورق فلزی مربع شکلی به طول ضلع ٣٠سانتی متر را درنظر بگیرید. مطابق شکل میخواهیم از چهارگوشه آن مربع های کوچکی به ضلع $x$ برش بزنیم و آنها را کنار بگذاریم. سپس با تا کردن ورق در امتداد خط چین های مشخص شده در شکل، یک جعبه درباز بسازیم. مقدار $x$ چقدر باشد تا حجم قوطی، حداکثر مقدار ممکن گردد؟

جواب: یک مکعب مستطیل داریم که سطح قاعده آن یک مربع به ضلع $l$ است و ارتفاع مکعب مستطیل برابر $x$ است. سوال از ما خواسته حجم قوطی ماکزیمم شود در حالی که طول ضلع ورق فلزی 30 سانتی متر است. در نتیجه اطلاعات مسئله را به صورت جدول زیر می نویسیم. که میبینیم که به ازای $x=5$ حجم مقدار ماکزیمم خود را دارد که این مقدار ماکزیمم برابر 2000 است.

$x+l+x=30\,\,\,\,,\,\,\,\, V=xl^{2}$

در گام بعد باید همه ی متغیرها را براساس یک متغیر تعریف کنیم. در نتیجه داریم:

$l=30-2x$

$\rightarrow V=x(30-2x)^{2}=4x^{3}-120x^{2}+900x$

از طرفی چون طول نمی تواند منفی باشد داریم:

$x,l \ge 0 \,\,\,\rightarrow \,\,\, 30-2x \ge 0 \,\,\,\rightarrow \,\,\, 0 \le x \le 15$

در گام بعد باید نقاط بحرانی یعنی نقاطی که مشتق تابع حجم را صفر می کنند یا تابع در آنها مشتق ندارد را بدست آوریم. از آنجاکه تابع حجم یک تابع درجه سه است بنابراین مشتق تابع حجم یک تابع درجه دو یا سهمی است. تابع درجه سه یک چندجمله ای است و در همه نقاط مشتق دارد. بنابراین برای بدست آوردن نقاط بحرانی آن کافیست نقاطی که مشتق آن ها صفر است را بدست آوریم. در نتیجه مشتق تابع حجم را بدست می آوریم:

$V=4x^{3}-120x+900x$

$\rightarrow V^{'}=12x^{2}-240x+900$

$\rightarrow V^{'}=0\,\,\,\rightarrow \,\,\, 12x^{2}-240x+900=0$

$\overset{\div 12}{\rightarrow}\,\,\,x^{2}-20x+75=0$

$\rightarrow (x-5)(x-15)=0\rightarrow x=5\,,\,x=15$

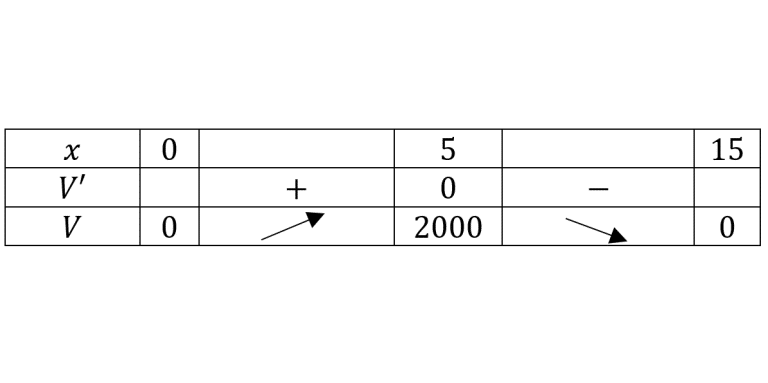
در گام بعد باید نقاط بحرانی که نقاط مرزی و نقاطی که مشتق را صفر می کنند هستند را بدست آوریم:

$x=0\,\,\,\,,\,\,\,\,x=5\,\,\,\,,\,\,\,\,x=15$

با توجه به جدول بالا می بینیم که $x=5$ منجربه ماکزیمم شدن تابع می شود که مقدار ماکزیمم تابع برابر 2000 است.

جمع بندی

در این مقاله به آموزش کاربرد مشتق در حل مسائل ریاضی پرداختیم. مسائلی از قبیل تشخیص صعودی یا نزولی بودن یک تابع، جهت تقعر یک تابع، رسم نمودار تابع و بهینه سازی یک تابع. اما برای حل این مسائل نیاز به دانستن یکسری پیش نیاز داریم از جمله اکسترمم های نسبی، اکسترمم های مطلق، نقاط بحرانی و آزمون مشتق اول. همه ی این موارد در این مقاله به طور کامل آموزش داده شده است. اگر نیاز به دانستن همه چیز در مورد مشتق دارید به مقاله مربوطه ارجاع کنید و اگر می خواهید بدانید کاربرد مشتق در حل مسائل چیست و چگونه می توان مسائل ریاضی را با کمک مشتق حل کرد این مقاله را از دست ندهید. در ضمن مارا از نظرات خود در مورد مقاله کاربرد مشتق در بهینه سازی و بدست آوردن اکسترمم و رسم توابع بهره مند کنید.

2 پاسخ

مریم گفت:

آوریل 16, 2025 در 07:11

سلام مرسی که فقط چیزهای اصلی رو گفتید گاهی کتاب ها آدم رو گیج می کنن وقتی کوتاه هست گیج نمیشم

پاسخ
1. ریحانه حسینی گفت:
  
  آوریل 16, 2025 در 17:23
  
  سلام عزیزم خوشحالم از مطالب راضی بودی
  
  پاسخ

کاربرد مشتق در بهینه سازی و بدست آوردن اکسترمم توابع، نقاط بحرانی و رسم توابع

چگونه اکسترمم نسبی یک تابع را بدست آوریم؟

چگونه نقطه بحرانی یک تابع را بدست آوریم؟

آزموش مشتق اول: تشخیص ماکزیمم نسبی یا مینیمم نسبی بودن یک نقطه بحرانی

چطور اکسترمم مطلق یک تابع را بدست آوریم؟

آزمون یکنوایی تابع: تشخیص صعودی یا نزولی بودن یک تابع

چطور جهت تقعر یک تابع و نقطه عطف آن را بدست آوریم؟

چطور با توجه به مشتق و کاربرد مشتق یک تابع را رسم کنیم؟

بهینه سازی: چطور با کمک کاربرد مشتق بهینه ترین حالت یک تابع را بدست آوریم؟

2 پاسخ

دیدگاهتان را بنویسید لغو پاسخ

آخرین مطالب وبلاگ

دنباله های عددی

تابع خطی و معادله خط

تابع و دامنه و برد آن

تعیین علامت

عبارت و معادله گویا

معادله درجه دوم

معادله

عبارت جبری

قدرمطلق

دوره ها

دسترسی سریع

دسترسی سریع

مقالات مادر