همه چیز را درباره ی حد و مجانب را در این آموزش رایگان بیاموزید.
مفهوم حد در ریاضیات برای بیان رفتار یک تابع، دنباله ای از اعداد یا یک سری مورد استفاده قرار می گیرد بررسی این رفتار در نقاط روی صفحه یا در بی نهایت صورت می گیرد. حد همچنین در حساب دیفرانسیل و انتگرال و نیز در آنالیز ریاضی برای تعریف پیوستگی، مشتق و انتگرال گیری مورد استفاده قرار می گیرد. در این مقاله به تعریف حد پرداختیم سپس حدهای یک طرفه را بررسی کردیم. همچنین در این مقاله به بررسی حدهای نامتناهی و حد در بینهایت پرداختیم. در اخر نکاتی درباره حد بیان کردیم تا از اشتباهات رایجی که ممکن است برای شما هم اتفاق بیفتد جلوگیری کنیم. اگر می خواهید همه چیز را درباره حد از تعریف و مفهوم آن در ریاضی تا همه ی قضایای مربوط به آن، حد توابع مثلثاتی، محاسبات حد درشرایط مختلف از جمله ایجاد شدن کسر صفر صفرم و مجانب ها بدانید هرگز این مقاله را از دست ندهید.
حد چیست؟ حد در زبان ریاضی چگونه تعریف می شود؟
حد و فرآیند حدی
مساحت چندضلعی های منتظم درون دایره محیطی را به هر اندازه که بخواهیم، می توانیم به مساحت دایره نزدیک کنیم، به شرط آنکه تعداد اضلاع را به اندازه کافی زیاد کنیم. عبارات به اندازه دلخواه و به اندازه کافی کلمات کلیدی در تعریف حد هستند. در این مثال باید تعداد اضلاع به حد کافی زیاد شوند تا مساحت به اندازه دلخواه به مساحت دایره نزدیک شود. در ادامه به تعریف مفهوم حد به زبان ریاضی می پردازیم.
مفهوم حد به زبان ریاضی
با توجه به مفهوم حد برای آنکه بتوان مقادیر متغیر را از دو طرف (چپ و راست) به عددی مانند نزدیک نمود کافی است تابع مورد نظر در یک بازه باز شامل
تعریف شده باشد. در محاسبات حد تابع در نقطه
، رفتار تابع در دو طرف نقطه
اهمیت دارد پس لزومی ندارد خود
در دامنه تابع باشد. برای این کار باید به تعریف همسایگی یک نقطه بپردازیم.
تعریف همسایگی یک نقطه
اگر یک عدد حقیقی باشد، هر بازه ی باز شامل
را یک همسایگی
می نامیم. بنابراین اگر
آنگاه بازه ی
یک همسایگی
است. اگر نقطه
را از این بازه حذف کنیم مجموعه
را همسایگی محذوف
می نامیم. به همین ترتیب اگر
در این صورت بازه
را یک همسایگی راست و بازه
را یک همسایگی چپ
می نامیم.
حد یک تابع چگونه تعریف می شود؟
فرض کنیم تابع در یک همسایگی عدد
به جز احتمالا در خود
تعریف شده باشد. می گوییم ” حد تابع
وقتی
به
نزدیک می شود برابر عدد حقیقی
است” هرگاه مقادیر تابع
را به هر اندازه ی دلخواه بتوان به
نزدیک کرد، به شرط آنکه متغیر
با مقادیر مخالف
از دو طرف به قدر کافی به
نزدیک شود. در این صورت می نویسیم
. عدد
را حد تابع
در نقطه
می نامیم.
حد های یکطرفه چگونه تعریف می شوند و بدست می آیند؟
تعریف حد راست
اگر تابع در یک همسایگی راست نقطه ای مانند تعریف شده باشد می گوییم ” حد راست تابع
در نقطه
برابر عدد حقیقی
است” هرگاه مقادیر تابع
را به هر اندازه ی دلخواه بتوان به
نزدیک کرد، به شرط آنکه متغیر
از سمت راست به قدر کافی به
نزدیک شود. در این صورت می نویسیم
تعریف حد چپ
اگر تابع در یک همسایگی چپ نقطه ای مانند
تعریف شده باشد می گوییم ” حد چپ تابع
در نقطه
برابر عدد حقیقی
است” هرگاه مقادیر تابع
را به هر اندازه ی دلخواه بتوان به
نزدیک کرد، به شرط آنکه متغیر
از سمت راست به قدر کافی به
نزدیک شود. در این صورت می نویسیم
تعریف حد به طور کلی و با توجه به حد چپ و راست
اگر تابع در همسایگی محذوف نقطه ای مانند
تعریف شده باشد آن گاه با توجه به مفهوم حد راست و حد چپ می توان گفت حد تابع
در نقطه
وجود دارد اگر و تنها اگر حد چپ و راست تابع
در
موجود و با هم برابر باشند.
در نتیجه اگر حد چپ و راست در نقطه
دو مقدار متمایز باشند آن گاه
در نقطه
حد ندارد.
نکته: اگر دو تابع و
در یک همسایگی راست نقطه ای مانند
با هم برابر باشند و حد راست یکی از آنها در
وجود داشته باشد آن گاه حد راست تابع دیگر نیز در
وجود دارد و مقدار این دو حد با هم برابرند یعنی: اگر
آن گاه
به طریق مشابه دو تابعی که در یک همسایگی چپ نقطه با هم برابرند مقدار حد چپ آن ها در نقطه
در صورت وجود در صورت وجود یکسان است.
بنابراین دو تابع که در یک همسایگی نقطه به جز احتمالا خود
با هم برابر باشند مقدار حد آنها در نقطه
در صورت وجود یکسان است.
قضایای حد: حد توابع مختلف چگونه بدست می آیند؟
حد تابع ثابت در هر عدد دلخواه
برابر مقدار ثابت
است یعنی :
حد تابع همانی در هر عدد دلخواه
برابر خود
است یعنی :
قضیه: برای هر عدد حقیقی ، داریم
قضیه : اگر دو تابع و
در نقطه
حد داشته باشند و
و
، آنگاه تعریف می کنیم:
*حد مجموع : مجموع این دو تابع در حد دارد و داریم :
*حد تفاضل: تفاضل این دو تابع در حد دارد و داریم :
*حد حاصل ضرب : حاصل ضرب این دو تابع در حد دارد و داریم:
*حد خارج قسمت: به شرط آنکه ، تابع
در
حد دارد و داریم :
تذکر : گاهی صورت یا مخرج تابع شامل یک عبارت رادیکالی است و
در این حالت برای محاسبه حد در نقطه
لازم است ابتدا صورت و مخرج را در یک عبارت رادیکالی ضرب کنیم تا عامل
یا عبارتی که موجب صفر شدن
و
شده است، در صورت و مخرج ظاهر شود تا با ساده کردن آن از صورت و مخرج، بتوانیم مقدار حد را در صورت وجود به دست آوریم.
توجه: در این موارد حالت برعکس الزاما صادق نیست مثلا اگر جمع یا تفاضل یا ضرب یا تقسیم دو تابع حد داشته باشند الزاما خود تابع ها حد ندارند.
قضیه : هر چند جمله ای مانند در هر نقطه دلخواه
حد دارد و مقدار حد با مقدار چند جمله ای در نقطه
برابر است. یعنی :
توجه: برای استفاده از قضیه حد مجموع حد تفاضل و … ابتدا باید توجه کنیم که حد توابع و
در نقطه
موجود باشند.
قضیه : فرض کنید تابع در نقطه
حد دارد. اگر تابع
در یک همسایگی محذوف
نامنفی باشد آنگاه داریم:
به طور کلی برای هر عدد طبیعی ، اگر
در یک همسایگی
تعریف شده باشد آنگاه داریم:
تذکر : همه ی قضایای بیان شده درباره حد (دوطرفه) برا ی حد چپ و حد راست نیز برقرارند.
حد توابع کسری وقتی کسر به صورت صفر صفرم است چگونه بدست می آید؟
برای محاسبه حد توابع کسری در حالت صفر تقسیم بر صفر دو راه داریم که در ادامه می بینیم:
راه اول : استفاده از اتحاد ها (اتحاد ها را می توانید در مقاله عبارت جبری بیاموزید) بخصوص مزدوج و چاق و لاغر و روابط مثلثاتی
راه دوم : استفاده از هوپیتال (مشتق از صورت و مخرج)
نکته: اگر در محاسبه که
و
دو چندجمله ای هستند، داشته باشیم:
دیگر با قانون اخیر نمی توان حد را محاسبه کرد. در این حالت به روش زیر عمل می کنیم:
اگر پس
و
بر
بخش پذیرند. ابتدا
را با تقسیم
و
بر
ساده می کنیم و سپس امکان استفاده از قانون تقسیم حد ها را بررسی می کنیم.
مثال: برای تعیین حد تابع هر دو راه حل را امتحان می کنیم. ابتدا از روش استفاده از اتحاد ها سعی به حل این حد کسری می کنیم. ابتدا مقدار صورت و مخرج کسر را به ازای
محاسبه می کنیم و می بینیم به کسر
می رسیم. حالا باید یک سری مرحله برای بدست آوردن مقدار حد طی کنیم. در مرحله اول صورت کسر را تجزیه می کنیم:
سپس مخرج کسر را تجزیه می کنیم:
حالا به مقداری که حد باید در آن محاسبه شود نگاه می کنیم:
پس حالا می دانیم عامل صفر کننده صورت و مخرج که در هر دو وجود دارد چیست :
. بنابراین با ساده کردن عامل صفر کننده می توانیم مقدار حد را حساب کنیم.
راه دوم استفاده از روش هوپیتال است. در این روش از مشتق برای بدست آوردن مقدار حد تابع استفاده می کنیم.
می بینیم در هر دو روش مقدار حد تابع کسری یکسان شد. اگر می توانید از اتحادها برای حل سوالات کمک بگیرید می توانید از هر دو روش استفاده کنید اما در بعضی سوالات استفاده از اتحادها زمانبر است در نتیجه بهتر است که حتما روش هوپیتال که بدست آوردن مشتق صورت به صورت جداگانه و نوشتن آن در صورت کسر جدید و بدست آوردن مشتق مخرج به صورت جداگانه و نوشتن آن در مخرج کسر جدید و بدست آوردن حد کسر جدید به جای کسر قبلی احتمالا روش بهتر و ساده تری خواهد بود.
حدهای نامتناهی: وقتی مقدار تابع از هر مقداری بزرگتر یا کوچکتر می شود.
اگر تابع در یک همسایگی عدد
به جز احتمالا در خود
تعریف شده باشد، آنگاه با به اندازه کافی نزدیک شدن
به
مقدار تابع
به اندازه دلخواه بزرگ شده باشد به این معنا که مقدار تابع از هر مقدار دلخواهی بزرگتر یا از هر مقدار دلخواهی کوچکتر باشد آنگاه می گوییم تابع
حد نامتناهی دارد. در ادامه به تعریف حدهای نامتناهی یکطرفه و ذکر نکاتی در این مورد می پردازیم.
تعریف: فرض کنید تابع در همسایگی محذوف
تعریف شده باشد در این صورت
یعنی اینکه می توانیم
را به میزان دلخواه از هر عدد مثبت بزرگتر کنیم به شرطی که
را به اندازه کافی به
نزدیک کرده باشیم.
تعریف: فرض کنید تابع در همسایگی محذوف
تعریف شده باشد در این صورت
یعنی اینکه می توانیم
را به میزان دلخواه از هر عدد منفی کوچکتر کنیم به شرطی که
را به اندازه کافی به
نزدیک کرده باشیم.
تعریف حدهای یکطرفه نامتناهی
حدهای یکطرفه نامتناهی چهار حالت دارند که در ادامه بررسی می کنیم:
*فرض کنیم تابع در یک همسایگی راست نقطه ای مانند
تعریف شده باشد در این صورت
بدین معنی است که می توانیم
را به دلخواه هر قدر بخواهیم از هر عدد مثبتی بزرگتر کنیم به شرطی که
را از سمت راست به اندازه کافی به
نزدیک کرده باشیم.
* فرض کنیم تابع در همسایگی چپ نقطه ای مانند
تعریف شده باشد در این صورت
بدین معنی است که می توانیم
را به دلخواه هر قدر بخواهیم از هر عدد مثبتی بزرگتر کنیم به شرطی که
را از سمت چپ به اندازه کافی به
نزدیک کرده باشیم.
*فرض کنیم تابع در یک همسایگی راست نقطه ای مانند
تعریف شده باشد در این صورت
بدین معنی است که می توانیم
را به دلخواه هر قدر بخواهیم از هر عدد منفی کوچکتر کنیم به شرطی که
را از سمت راست به اندازه کافی به
نزدیک کرده باشیم.
* فرض کنیم تابع در همسایگی چپ نقطه ای مانند
تعریف شده باشد در این صورت
بدین معنی است که می توانیم
را به دلخواه هر قدر بخواهیم از هر عدد منفی کوچکتر کنیم به شرطی که
را از سمت چپ به اندازه کافی به
نزدیک کرده باشیم.
- نماد
نشان می دهد که حد فوق موجود نیست. چون مقدار تابع به عدد خاصی نزدیک نمی شود و مثبت بینهایت فقط یک نماد است که نشان می دهد مقدار تابع از هر عدد مثبتی می تواند بزرگتر باشد.
تذکر: تعریف حدهای یک طرفه نامتناهی و
نیز مشابه تعاریف فوق است.
حالت های مختلف حدهای یک طرفه نامتناهی در شکل های زیر آمده است:
برخی از قضایای حدهای بینهایت
قضیه 1: اگر یک عدد طبیعی باشد آن گاه
قضیه 2: اگر و
آن گاه
و برعکس.
همچنین اگر و
آن گاه
و برعکس.
قضیه 3: اگر و
آن گاه:
*اگر و مقادیر
در همسایگی محذوف
مثبت باشد آن گاه:
*اگر و مقادیر
در همسایگی محذوف
مثبت باشد آن گاه:
*اگر و مقادیر
در همسایگی محذوف
منفی باشد آن گاه:
*اگر و مقادیر
در همسایگی محذوف
منفی باشد آن گاه:
تذکر : قضیه 3 در حالتی که یا
نیز برقرار است.
قضیه 4: اگر و
و یا
آن گاه:
تذکر : قضیه 4 در حالتی که یا
نیز برقرار است.
قضیه 5: اگر و
آن گاه:
*اگر آنگاه
*اگر آن گاه
تذکر : قضیه 5 در حالتی که یا
نیز برقرار است.
حد در بینهایت چگونه تعریف می شود و بدست می آید؟
تعریف : اگر تابع در بازه ای مانند
تعریف شده باشد گوییم حد
وقتی
به سمت مثبت بینهایت میل می کند برابر
است و می نویسیم
هرگاه بتوان با اختیار
های به قدر کافی بزرگ فاصله
را از
را به هر اندازه کوچک کرد.
اگر تابع در بازه ای مانند
تعریف شده باشد گوییم حد
وقتی
به سمت منفی بینهایت میل می کند برابر
است و می نویسیم
هرگاه بتوان با اختیار
های به قدر کافی کوچک فاصله
را از
را به هر اندازه کوچک کرد.
قضیه 6: اگر عددی حقیقی و
عددی طبیعی باشد آنگاه:
قضیه 7 : اگر و
اعداد حقیقی و
و
آنگاه :
تذکر : قضیه 7 وقتی هم برقرار است.
حد نامتناهی در بی نهایت
قضیه 8: اگر عددی طبیعی باشد آن گاه:
قضیه 9: اگر عددی حقیقی (ناصفر) و
و
آن گاه:
تذکر: قضیه 9 در حالتی که نیز به طرق مشابه است.
قضیه 10: اگر عددی حقیقی (ناصفر) و
و
آن گاه :
تذکر: قضیه 10 در حالتی که نیز به طرق مشابه است.
نکته: به طور کلی حد هر چند جمله ای بصورت در
برابر حد جمله ای از آن است که دارای بزرگترین درجه است یعنی :
نکته: به طور کلی هر چند جمله ای بصورت حد دارد و مقدار حد با مقدار چند جمله ای در نقطه
برابر است. یعنی:
برای استفاده از قضیه حد مجموع حد تفاضل و … ابتدا باید توجه کنیم که حد توابع و
در نقطه
موجود باشند.
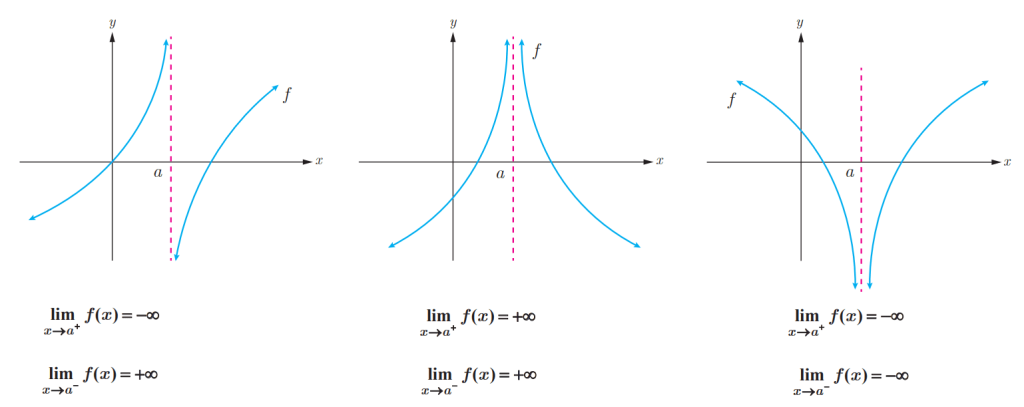
چطور مجانب قائم یک تابع را بدست آوریم؟
خط را مجانب قائم نمودار تابع
می گویند هرگاه حداقل یک از شرایط زیر برقرار باشد.
در شکل های زیر خط مجانب قائم منحنی است.
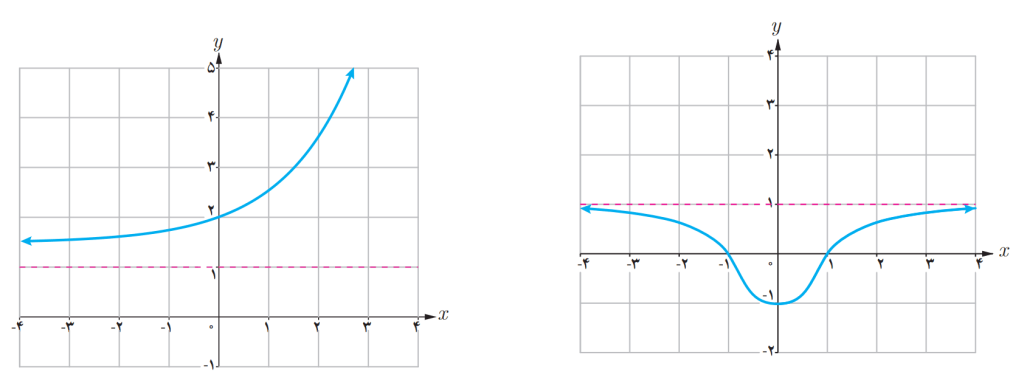
چطور مجانب افقی یک تابع را بدست آوریم؟
خط را مجانب افقی نمودار
می نامیم به شرطی که حداقل یکی از دو شرط زیر برقرار باشد:
در شکلهای زیر خط مجانب افقی منحنی است.
چند نکته برای فهم بهتر حد توابع
چند نکته در باره حد توابع
- تابع لازم نیست که در نقطه حدی خود تعریف شده باشد.
- لازم نیست مقدار تابع در نقطه حدی با مقدار حدش در آن نقطه برابر باشد.
- حد تابع، همان مقدار تابع در آن نقطه نیست.
- حد به عنوان مقداری غیرقابل دسترس محسوب نمی شود بلکه کاملا قابل محاسبه است.
- حد، یک نقطه مرزی نیست و مقدار تابع به ازای تمامی مقادیر تعریف شده در دامنه آن می تواند از حد تابع کوچکتر یا بزرگتر یا مساوی باشد.
- حد، مقدار تقریبی نیست بلکه یک مقدار دقیق است که می توان آن را بدست آورد.
- هر تابعی در هر نقطه ای می تواند حد داشته باشد لازم نیست تابع الزاما پیوسته باشد کافی است که شرایط داشتن حد وجود داشته باشد.
جمع بندی
در این مقاله به بیان مفهوم حد در ریاضی پرداختیم در این بین به بیان حدهای یک طرفه، حد در بینهایت، حد های مثلثاتی، قضایای حد و حد نامتناهی پرداختیم. در ضمن به بیان یکی از چالش های کسر یعنی صفر صفرم پرداختیم و دو راه حل برای آن بیان کردیم. همچنین در ادامه ی حدِ بینهایت و حد در بینهایت به بیان مجانب افقی و مجانب قائم پرداختیم. در ادامه ی حد بهتر است سراغ پیوستگی، مشتق و کاربرد مشتق در بهینه سازی و اکسترمم توابع بروید تا علم خود را در حوزه دیفرانسیل بیشتر کنید. لطفا نظرات خود را درباره مقاله حد و مجانب در قسمت کامنت ها بیان کنید.

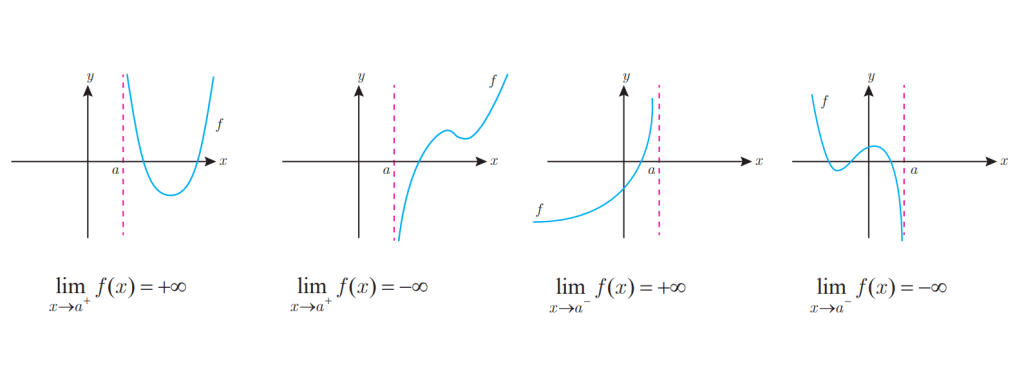
![Rendered by QuickLaTeX.com \[\lim_{x \to 0^{-}}{\frac{1}{x^{n}}}=\begin{cases} +\infty & n \in \Bbb{E} \\ -\infty & n \in \Bbb{O} \end{cases}\]](https://faramath.com/core/ql-cache/quicklatex.com-a0833f30b9f2798222040b75c0b4a1b1_l3.png)
![Rendered by QuickLaTeX.com \[n \in \Bbb{O} \,\,\,\rightarrow \,\,\, \begin{cases} \lim_{x \to +\infty}{x^{n}}=+\infty \\ \lim_{x \to -\infty}{x^{n}}=-\infty \end{cases}\]](https://faramath.com/core/ql-cache/quicklatex.com-56757eebd79de72177b6e7b44c7fb679_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{x \to +\infty}{f(x)}.\lim_{x \to +\infty}{g(x)}=\begin{cases} +\infty & l > 0 \\ -\infty & l < 0 \end{cases}\]](https://faramath.com/core/ql-cache/quicklatex.com-d3a8f7a0ff1ec23e3c58393088c461c0_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{x \to -\infty}{f(x)}.\lim_{x \to -\infty}{g(x)}=\begin{cases}+\infty & l > 0 \\ -\infty & l < 0 \end{cases}\]](https://faramath.com/core/ql-cache/quicklatex.com-c8a53b7576a449850e0156c7723b2bc1_l3.png)

2 پاسخ
اقا خیلی ممنونم جدا حد رو یاد گرفتم فقط مونده چند تا چیز رو از مقاله حفظ کنم
خوشحالم یاد گرفتی موفق باشی عزیزم