کامل ترین و بهترین آموزش درمورد گزاره ها (هرآنچه لازم است درباره گزاره ها بدانید)

گزاره ها یک سری عبارت خبری هستند که ممکن است درست یا نادرست باشند. در این مقاله آموزش می دهیم که گزاره چیست. جدول ارزش گزاره چطور رسم می شود. نقیض گزاره ، ترکیب فصلی دو گزاره ، ترکیب عطفی دو گزاره ، گزاره شرطی و گزاره دو شرطی در این مقاله آموزش داده می شود. همچنین این مقاله قوانین هم ارزی مانند قوانین دمورگان، جذب، جابجایی، شرکت پذیری و توزیع پذیری را آموزش داده است. سورها مبحث دیگری در گزاره ها هستند که در آخر توضیح داده شده اند. امیدواریم از خواندن این مقاله لذت ببرید و این مقاله برای شما مفید واقع شود.

گزاره چیست؟

منطق ریاضی که عده ای به آن منطق نمادین ـ $Symbolic-Logic$ نیز می گویند، دستور زبان ریاضی، یا مطالعه ساختار جمله هایی است که در ریاضی به کار برده می شود. این شاخه از ریاضیات به بررسی دقیق استدلال ها می پردازد و اعتبار یک استدلال را مشخص می کند.

در منطق ریاضی به جملات خبری نخست، مفروضات استدلال و به جمله خبری آخر، نتیجه استدلال گفته می شود. یک استدلال می تواند از چندین جمله خبری تشکیل شود که یکی از آنها نتیجه استدلال و بقیه، مفروضات استدلال اند.

به جمله خبری که درحال حاضر یا آینده، دارای ارزش درست یا نادرست (راست یا دروغ) باشد، گزاره می گویند. معمولا گزاره ها $p,q,r,…$ نشان می دهند. جمله های پرسشی، امری و عاطفی (نشان دهنده احساسات) گزاره محسوب نمی شوند؛ زیرا خبری را بیان نمی کنند.

درست یا نادرست بودن یک گزاره را ارزش گزاره می گوییم. ارزش گزاره درست را با $T$ و گزاره نادرست را با حرف $F$ نشان می دهند.

یک گزاره نمی تواند هم درست و هم نادرست باشد؛ یعنی هر گزاره فقط یک ارزش دارد.

جدول ارزش گزاره ها چگونه رسم می شود؟

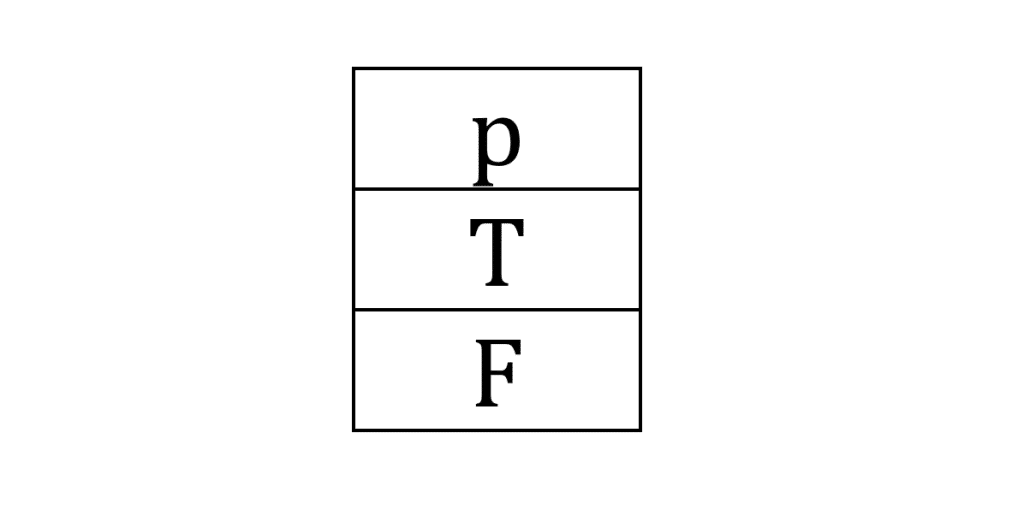
هر گزاره دارای ارزش درست یا نادرست است؛ بنابراین، هر گزاره مانند $p$ فقط یکی از دو حالت ارزش گزاره را طبق جدول روبه رو می گیرد.

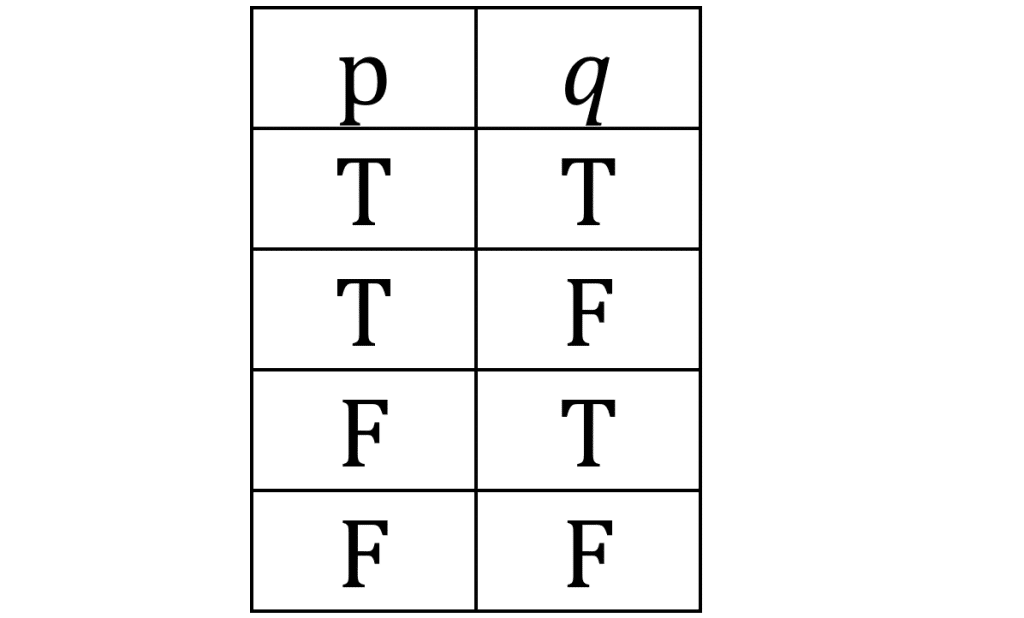
ارزش های دو گزاره به صورت زیر است:

ارزش های $n$ گزاره برابر با $2^{n}$ حالت دارد.

هر جمله خبری که شامل یک یا چند متغیر است و با جایگذاری مقادیری به جای متغیر به یک گزاره تبدیل شود، گزاره نما نامیده می شود. گزاره نماها را برحسب تعداد متغیر به کار رفته در آنها، یک متغیره، دو متغیره و … می نامیم.

در هر گزاره نما به مجموعه ی مقادیری که می توان آنها را به جای متغیرهای آن قرار داد، تا اینکه گزاره نما به گزاره تبدیل شود، دامنۀ متغیر $Domain-of-Variable$ گزاره نما می گویند و آن را با حرف $D$ نمایش می دهند.

در هر گزاره نما، به مجموعه عضوهایی از دامنه متغیر که به ازای آنها، گزاره نما تبدیل به گزاره ای با ارزشِ درست شود، مجموعه جواب $Answer-Set$ گزاره نما می گویند و آن را با حرف $S$ نمایش می دهند و همواره داریم $S \subseteq D$ .

از ترکیب دو یا چند گزاره به وسیله رابط های گزاره ای (ادات ربط)، گزاره های مرکب به دست می آیند. در ادامه گزاره های مرکب عطفی ، فصلی، شرطی و دو شرطی را بیان می کنیم.

نقیض گزاره چگونه بدست می آید؟

نقیض گزارە $p$ به صورت $\sim p$ نوشته می شود و آن را “چنین نیست که $p$ ” می خوانیم. اگر ارزش گزاره $p$ درست باشد آنگاه ارزش $\sim p$ غلط است. اگر ارزش گزاره $p$ غلط باشد $\sim p$ درست است.

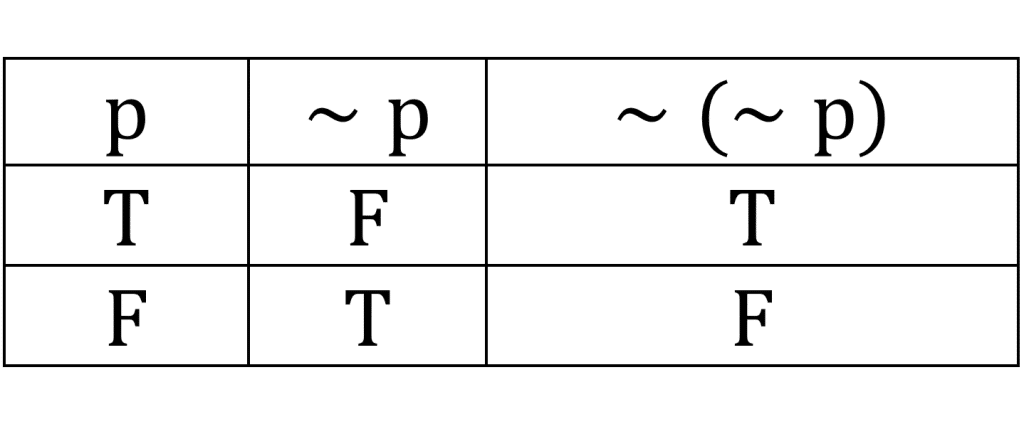
به علامت $\sim$ ناقض می گویند و “چنین نیست که” خوانده می شود.

همانطور که از جدول بالا مشخص است $\sim(\sim p)\equiv p$ می باشد. می خوانیم نقیض نقیض $p$ هم ارز منطقی با $p$ .

در حالت کلی اگر دو گزاره $p$ و $q$ هم ارزش باشند می نویسیم $p \equiv q$ و می خوانیم $p$ هم ارز است با $q$ .

ترکیب فصلی دو گزاره چگونه بدست می آید؟

هر گاه $p$ و $q$ دو گزاره باشند، به گزاره مرکب $p$ یا $q$ را که به صورت $p \lor q$ می نویسند ترکیب فصلی دو گزاره می گوییم.

در اینجا به رابط منطقی $\lor$ فاصل گفته می شود. ارزش گزاره $p \lor q$ فقط وقتی نادرست است که ارزش هر دو گزاره ی $p$ و $q$ نادرست باشند. جدول زیر ارزش گزاره $p \lor q$ را نشان می دهد.

ترکیب عطفی دو گزاره چگونه بدست می آید؟

هر گاه $p$ و $q$ دو گزاره باشند، به گزاره مرکب $p$ و $q$ را که به صورت $p \land q$ می نویسند ترکیب عطفی دو گزاره می گوییم.

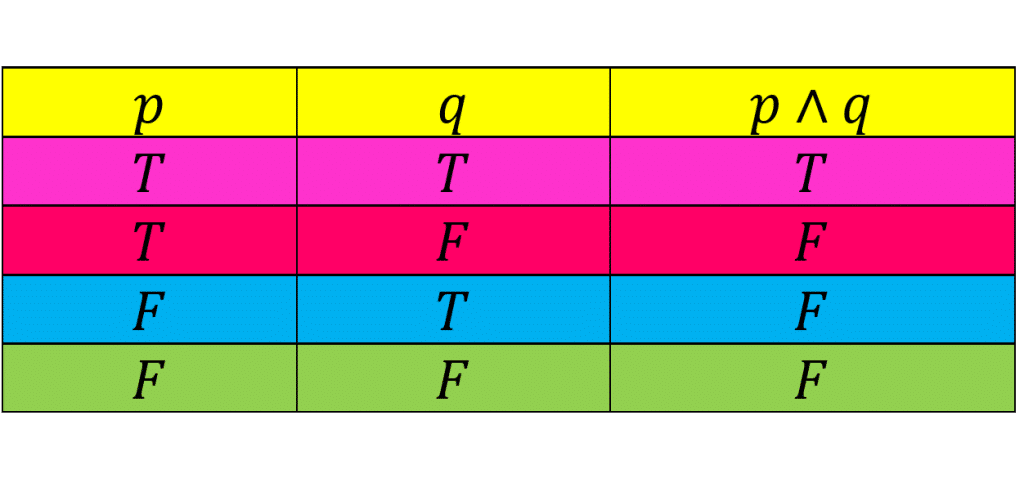
در اینجا به رابط منطقی $\land$ عطف گفته می شود. ارزش گزاره $p \land q$ فقط وقتی درست است که ارزش هر دو گزاره ی $p$ و $q$ درست باشند. جدول زیر ارزش گزاره $p \land q$ را نشان می دهد.

ترکیب شرطی دو گزاره چیست؟

هر گاه $p$ و $q$ دو گزاره باشند، به گزاره مرکب ” اگر $p$ آنگاه $q$ ” را که به صورت $p \Rightarrow q$ می نویسند ترکیب شرطی دو گزاره می گوییم. در این ترکیبِ شرطی $p$ را مقدم (فرض) و $q$ را تالی (حکم ) می نامیم.

گزاره مرکب $p \Rightarrow q$ را به صورت های $p$ شرط کافی برای $q$ است و $q$ شرط لازم برای $p$ است نیز می خوانیم.

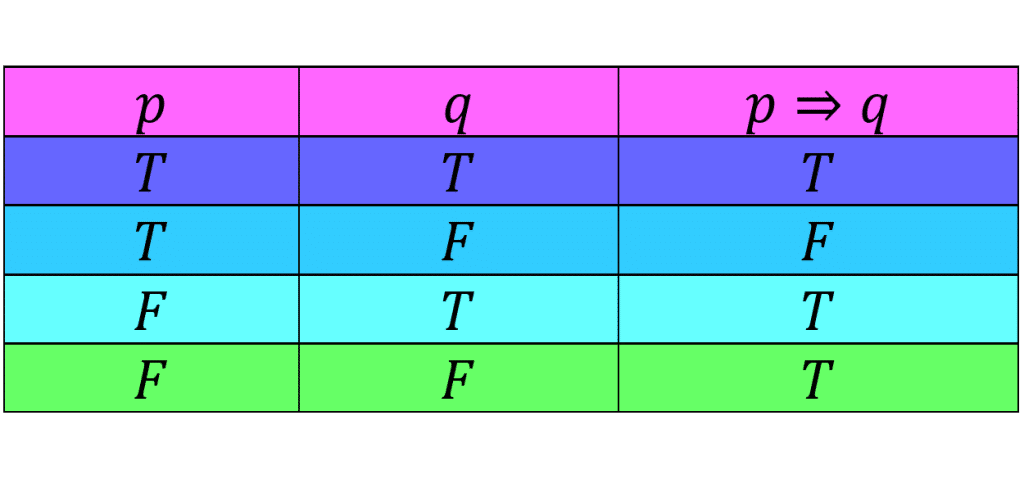
اگر ارزش $p$ (مقدم) نادرست باشد آنگاه ارزش گزاره مرکب $p \Rightarrow q$ همواره درست است و ارزش آن به $q$ بستگی ندارد. در این حالت می گویند ارزش $p \Rightarrow q$ به انتفای مقدم درست است. ارزش $p \Rightarrow q$ وقتی نادرست است که $p$ درست و $q$ نادرست باشد. جدول زیر ارزش گزاره $p \Rightarrow q$ را نشان می دهد.

نکته: باید بدانیم ارزش گزاره شرطی معادل با یک ترکیب فصلی از تالی و نقیض مقدم است.

$p \Rightarrow q \equiv \sim p \lor q$

توجه: گزاره $q \Rightarrow p$ عکس ترکیب شرطی $p \Rightarrow q$ و گزاره $\sim q \Rightarrow \sim p$ عکس نقیض ترکیب شرطی $p \Rightarrow q$ است. عکس نقیض گزاره شرطی با خودش هم ارزش است.

در بعضی از اثبات ها که مشکل هستند بهتر است از اثباتِ ” عکس نقیض عبارت شرطی سوال” که راحت تر است استفاده کنیم و از درستی آن درستی حکم اصلی را نتیجه بگیریم.

مثال: اثبات کنید اگر $n^{2}$ زوج باشد آنگاه $n$ زوج است.

جواب: در این سوال یک گزاره شرطی در سوال مطرح شده که مقدم آن ” $n^{2}$ زوج است” و تالی آن ” $n$ زوج” است. اثبات این سوال سخت است بنابراین به جای این گزاره شرطی از عکس نقیض آن استفاده می کنیم. یعنی نقیض مقدم برابر است با ” $n^{2}$ فرد است” و نقیض تالی برابر است با ” $n$ فرد است” پس صورت سوال به عکس نقیض سوال تغییر می کند:

اثبات کنید اگر $n$ فرد باشد آنگاه $n^{2}$ فرد است. حالا این سوال جدید را حل می کنیم:

اگر یک عدد فرد باشد یعنی باقی مانده آن در تقسیم بر دو برابر با یک است پس می توان عدد فرد را به صورت $n=2k+1$ نشان می دهیم بنابراین $n^{2}$ را با جایگذاری عبارت $2k+1$ به جای $n$ بدست می آوریم. داریم:

$n^{2}=(2k+1)^{2}=4k^{2}+4k+1$

$=2(2k^{2}+2k)+1=2r+1$

اگر به جای عبارت $2k^{2}+2k$ قرار دهیم $r$ می توانیم بنویسیم: $n^{2}=2r+1$ بنابراین $n^{2}$ به صورت یک عدد فرد نمایش داده می شود. بنابراین اثبات انجام شد.

چند نکته درباره گزاره های مرکب

در ادامه چند نکته راجع به انواع گزاره های مرکب بیان می کنیم:

عکس نقیض هر گزاره شرطی با خودش هم ارزش است.

$p \Rightarrow q \equiv \sim q \Rightarrow \sim p$

در گزاره شرطی اگر تالی حاصل ترکیب فصلی مقدم با گزاره دلخواه دیگر باشد حاصل گزاره شرطی حتما درست است چرا که اگر مقدم درست باشد تالی هم درست می شود چون ترکیب فصلی گزاره درست با هر گزاره دلخواه درست است:

$p \Rightarrow (p \lor q) \equiv T$

در گزاره شرطی اگر مقدم ترکیب عطفی تالی با هر گزاره دلخواه باشد حتما ارزش گزاره شرطی درست می شود چون تنها در صورتی مقدم درست است که تالی هم درست باشد. چون ترکیب عطفی دو گزاره تنها زمانی درست است که هر دو گزاره درست باشد:

$(p \land q) \Rightarrow p \equiv T$

در گزاره شرطی اگر مقدم و تالی ارزش یکسان داشته باشند حتما ارزش گزاره شرطی درست است:

$p \Rightarrow p \equiv T$

ترکیب فصلی هر گزاره با نقیضش حتما درست است چراکه یا خود گزاره درست است یا نقیض اش و از آنجا که در ترکیب فصلی کافیست که یکی از دو گزاره درست باشد تا ارزش گزاره فصلی درست شود.

$p \lor \sim p \equiv T$

ترکیب عطفی هر گزاره با نقیضش حتما نادرست است چراکه یا خود گزاره نادرست است یا نقیض اش و از آنجا که در ترکیب عطفی کافیست که یکی از دو گزاره نادرست باشد تا ارزش گزاره عطفی نادرست شود.

$p \land \sim p \equiv F$

ترکیب دوشرطی دو گزاره چگونه انجام می شود؟

هر گاه $p$ و $q$ دو گزاره باشند، گزاره مرکب $(p \Rightarrow q ) \land (q \Rightarrow p)$ را به صورت $p \Leftrightarrow q$ می نویسیم و آن را ترکیب دو شرطی $p$ و $q$ می نامیم. گزاره مرکب $p \Leftrightarrow q$ را به صورت ” اگر $p$ آنگاه $q$ و برعکس ” ، ” $p$ شرط لازم و کافی برای $q$ است” یا” $p$ اگر و تنها اگر $q$ ” می خوانیم.

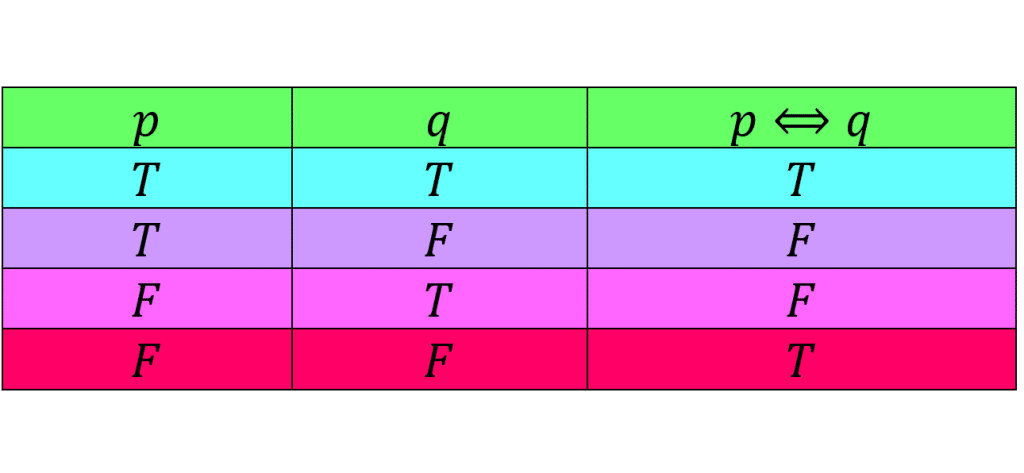
جدول زیر ارزش گزاره $p \Leftrightarrow q$ را نشان می دهد.

می بینیم ارزش گزاره دو شرطی در زمان هایی که دو گزاره هم ارزش اند ( فارغ از اینکه دو گزاره هر دو درست یا هر دو نادرست باشند) درست است و اگر دو گزاره ارزش های متفاوتی با هم داشته باشند آنگاه ارزش گزاره دو شرطی نادرست است.

قوانین هم ارزی

در این بخش به بررسی برخی از قوانین هم ارزی در گزاره ها می پردازیم:

قانون دمورگان: طبق این قانون می توان از علامت نقیض فاکتور گرفت. البته توجه به این نکته حائز اهمیت است که نقیض ترکیب فصلی، ترکیب عطفی است و بالعکس.

$\sim p \land \sim q \equiv \sim (p \lor q )$

$\sim p \lor \sim q \equiv \sim (p \land q)$

قانون جابجایی: طبق این قانون در ترکیب فصلی و عطفی فرقی نمی کند که کدام گزاره را اول بنویسیم.

$p \lor q \equiv q \lor p$

$p \land q \equiv q \land p$

قانون شرکت پذیری: طبق این قانون اگر سه گزاره داشته باشیم که بین شان دو به دو ترکیب فصلی ( یا عطفی) انجام شده باشد فرقی نمی کند که اول نتیجه ترکیب کدام دو گزاره را حساب کنیم.

$(p \lor q) \lor r \equiv q \lor (p \lor r)$

$(p \land q) \land r \equiv q \land (p \land r)$

قوانین توزیع پذیری: طبق این قانون اگر سه گزاره داشتیم و دو تایشان با هم ترکیب فصلی (یا عطفی) شدند و قرار بر این شد که حاصل این ترکیب که در پرانتز نمایش داده می شود با گزاره دیگری ترکیب عطفی (یا فصلی) پیدا کند آنگاه می توانیم از روابط زیر برای ساده سازی استفاده کنیم.

$p \land ( q \lor r ) \equiv (p \land q) \lor ( p \land r)$

$p \lor ( q \land r ) \equiv (p \lor q) \land ( p \lor r)$

چه نوع سورهایی داریم؟

عبارتهای “به ازای هر” و “به ازای بعضی مقادیر” به سور معروف اند. این عبارت ها می توانند قبل از گزاره نماها قرار گیرند و به این وسیله گزاره هایی با ارزش درست یا نادرست ایجاد کنند.

برای بیان عبارت ها با استفاده از نمادهای ریاضی به جای “به ازای هر”، یا “به ازای جمیع مقادیر”یا ” All ” از نماد $\forall$ استفاده می شود. به $\forall$ سور عمومی می گویند.

به جای “وجود دارد”، یا “به ازای بعضی مقادیر” یا ” Exist ” از نماد $\exists$ استفاده می شود. به $\exists$ سور وجودی می گویند.

یادآوری: مجموعه اعداد زوج را با $\Bbb{E}$ و مجموعه اعداد فرد را با $\Bbb{O}$ و مجموعه اعداد اول را با $\Bbb{P}$ نمایش داده می شوند.

گزاره نمای شامل متغیر $x$ که با سور عمومی همراه می شود وقتی به یک گزاره درست تبدیل می شود که هر عضو از دامنه متغیر در گزاره نما صدق کند به عبارت دیگر هیچ مثال نقضی نداشته باشد.

گزاره نمای شامل متغیر $x$ که با سور وجودی همراه می شود وقتی به یک گزاره درست تبدیل می شود که مجموعه جواب آن تهی نباشد.

نقیض ” هر عدد فرد مجذور کامل است” را به کمک سورها بنویسید؟ اول خود عبارت را به زبان ریاضی می نویسیم: $\forall x \in \Bbb{O} ; F(x)$ و تعریف می کنیم که $F(x)$ مجذور کامل بودن $x$ را نشان می دهد.

برای اینکه نقیض آن را بدست آوریم کافی است ثابت کنیم برای همه ی $x$ ها این گزاره غلط است کافی است یک مثال نقض (در مقاله استدلال ریاضی می توانید راجع به مثال نقض بخوانید) برای این موضوع وجود دارد. بنابراین می توان نوشت ” وجود دارد $x$ ای که مجذور کامل نباشد” به زبان ریاضی می توان نوشت: $\exists x \in \Bbb{O}; \sim F(x)$ .

جمع بندی

در این مقاله گزاره ها و ترکیب فصلی، عطفی، شرطی و دو شرطی آموزش داده شده است. نکاتی در مورد هر کدام از این ترکیب ها بیان شده است و همچنین قوانین هم ارزی مانند دمورگان، جذب و … بیان شده. سورها نیز در این مقاله آموزش داده شده. امیدواریم از مقاله گزاره که به آموزش رایگان مبحث گزاره ها پرداخته است لذت برده باشید. لطفا در قسمت کامنت ها نظرات و پیشنهادات خود را بیان کنید.

کامل ترین و بهترین آموزش درمورد گزاره ها (هرآنچه لازم است درباره گزاره ها بدانید)

گزاره چیست؟

جدول ارزش گزاره ها چگونه رسم می شود؟

نقیض گزاره چگونه بدست می آید؟

ترکیب فصلی دو گزاره چگونه بدست می آید؟

ترکیب عطفی دو گزاره چگونه بدست می آید؟

ترکیب شرطی دو گزاره چیست؟

چند نکته درباره گزاره های مرکب

ترکیب دوشرطی دو گزاره چگونه انجام می شود؟

قوانین هم ارزی

چه نوع سورهایی داریم؟

دیدگاهتان را بنویسید لغو پاسخ

آخرین مطالب وبلاگ

دنباله های عددی

تابع خطی و معادله خط

تابع و دامنه و برد آن

تعیین علامت

عبارت و معادله گویا

معادله درجه دوم

معادله

عبارت جبری

قدرمطلق

دوره ها

دسترسی سریع

دسترسی سریع

مقالات مادر