جامع ترین آموزش در حوزه هندسه تحلیلی، خط، نقطه، زاویه صفحه و فضا

هندسه تحلیلی علمی در حوزه خط، نقطه، زاویه، نیمساز، عمود منصف، خطوط موازی، خطوط عمود بر هم، صفحه، روابط خطوط با صفحه، فاصله دو نقطه و فاصله یک نقطه از خط می باشد. در این مقاله به بررسی هر کدام از این بخش ها پرداختیم. اگر علاقمند به دانستن همه چیز در مورد انواع خط، انواع زاویه، نیمساز و عمود منصف هستید اگر می خواهید بدانید خطوط با یکدیگر و با صفحات چه روابطی می توانند داشته باشند و اگر می خواهید بدانید چطور فاصله دو نقطه از هم و فاصله یک نقطه از خط را بدست آورید هرگز این مقاله را از دست ندهید.

هندسه ترسیمی چیست؟

هندسه ترسیمی عبارت است از نمایش یک نقطه، خط، سطح یا جسم با تصاویر دو بعدی از آن. در این مقاله به نمایش خط و زاویه می پردازیم. همچنین نحوه رسم نیمساز و عمود منصف را بیان می کنیم.

خطوط چند دسته اند؟

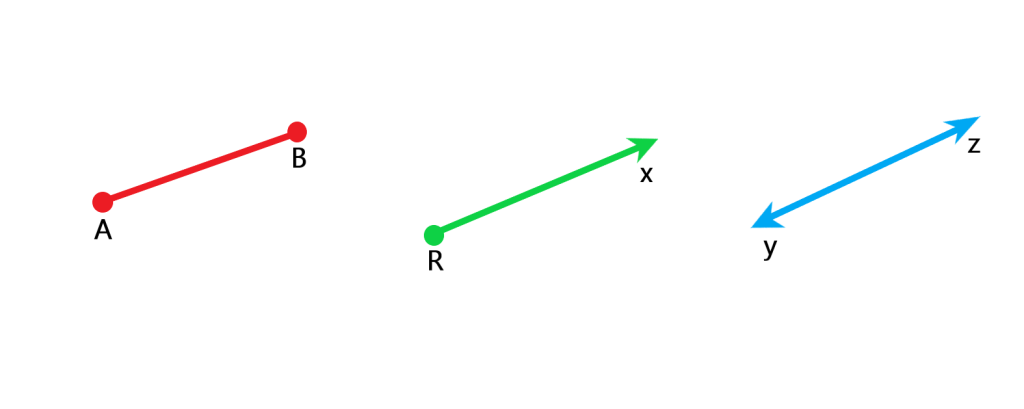
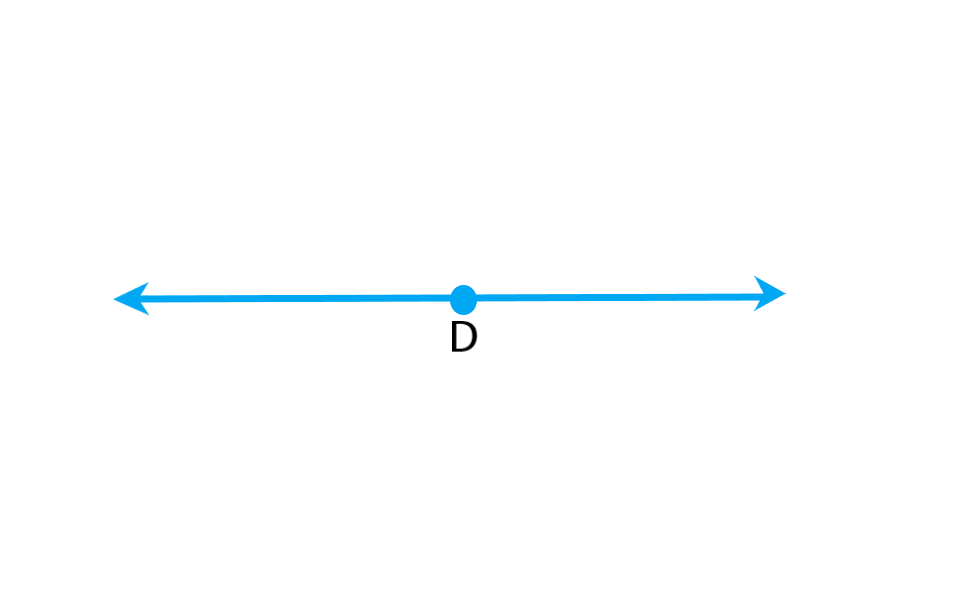
به طور کلی سه نوع خط داریم. اگر خطی را بتوان از دو طرف ادامه داد به آن “خط” می گوییم. اگر یک طرف خط با یک نقطه بسته شده باشد به آن “نیم خط” می گوییم. اگر هر دو طرف خط با نقطه بسته شده باشد به آن “پاره خط” می گوییم.

در شکل های زیر شکل آبی یک خط را نشان می دهد شکل سبز رنگ یک نیم خط را نشان می دهد و شکل قرمز رنگ یک پاره خط را نشان می دهد. البته باید بدانیم در ریاضیات برای نام گذاری شکل ها از حروف انگلیسی استفاده می کنیم. به طور معمول نقطه را با حروف بزرگ انگلیسی نام گذاری می کنیم و برای نام گذاری امتداد خط که در شکل با پیکان نشان می دهیم از حروف کوچک استفاده می کنیم.

طول یک پاره خط را با قرار دادن یک پاره خط کوچک در بالای نام آن نمایش می دهیم. مثلا $\overline{AB}$ یعنی طول پاره خط $AB$ . در پاره خط $AB$ به نقاط $A$ و $B$ دو سر پاره خط یا نقاط انتهایی پاره خط می گویند.

نکته: اگر سه نقطه $A$ و $B$ و $C$ روی یک خط قرار نداشته باشند یعنی می توان با وصل کردن آنها بهم یک مثلث ساخت. این مثلث $ABC$ نام دارد و آن را به صورت $\triangle ABC$ نمایش می دهیم. همیشه در هر مثلث مجموع اندازه های دو ضلع دلخواه از ضلع سوم بزرگتر است.

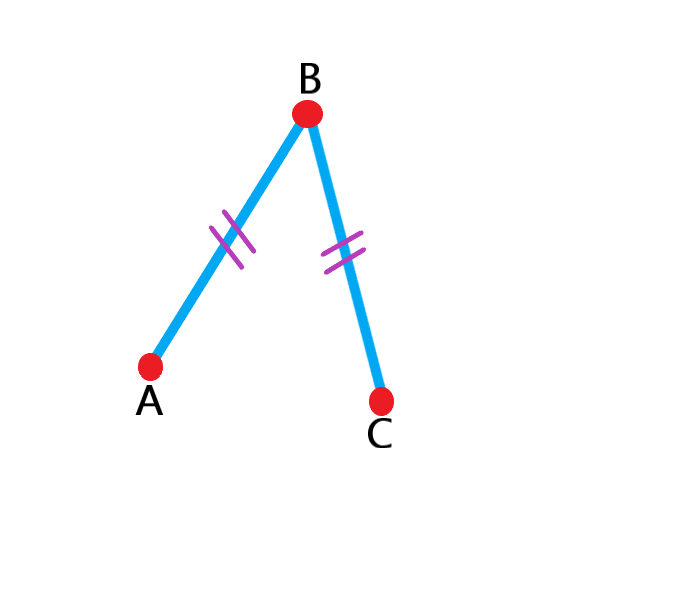
توجه: پاره خط های مساوی را به صورت زیر نشان می دهند در این شکل

$\overline{AB}=\overline{AC}$

باید چند نکته در مورد خطوط بدانید:

از یک نقطه بیشمار خط می گذرد.
از دو نقطه فقط یک خط در صفحه می گذرد.
برای اینکه یک خط در صفحه مشخص باشد باید حداقل دو نقطه از آن خط مشخص باشد.
خط راست از هر دو طرف نامحدود است.

زاویه چیست و چه انواعی دارد؟

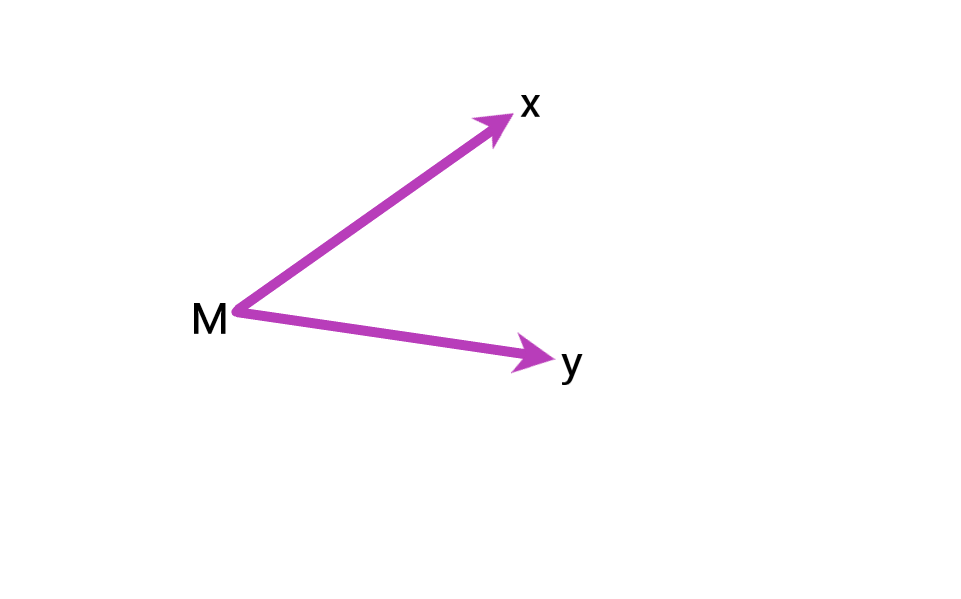
هر زاویه یک راس و دو ضلع (نیم خط) دارد. زاویه ها را به سه صورت نام می برند. مثلا به زاویه زیر می توان گفت زاویه $xMy$ یا زاویه $yMx$ یا زاویه $M$ .

اندازه گیری یک زاویه

نقاله وسیله ای است که زاویه ها را اندازه گیری می کند. نیم دایره ی نقاله به 180 قسمت مساوی تقسیم شده است. به هر کدام از این قسمت های کوچک (یعنی $\frac{1}{180}$ نیم دایره) یک درجه می گویند. ده درجه را بصورت $10^\circ$ می نویسیم. توجه کنید که یکی از واحدهای اندازه گیری زاویه درجه است واحد دیگر رادیان است که در بخش مثلثات می توانید با آن آشنا شوید.

اندازه یک زاویه به طول نیم خط های زاویه ربطی ندارد فقط به میزان بازشدگی دو نیم خط بستگی دارد که این میزان ِ بازشدگی به وسیله ی نقاله اندازه گیری می شود.

زوایای معروف

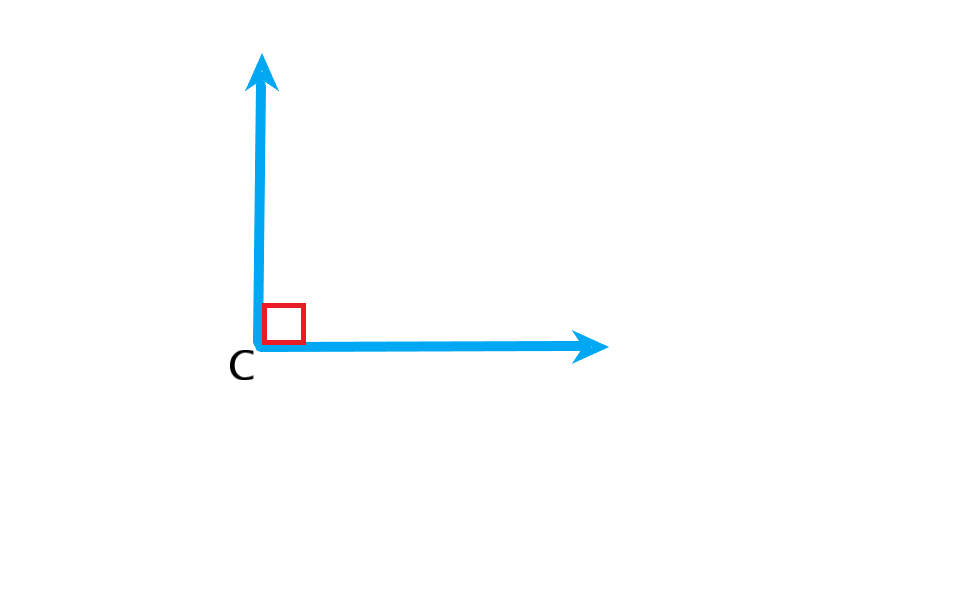
زاویه راست: زاویه ای که شبیه گوشه ی کتاب یا گوشه ی گونیاست، اگر با نقاله اندازه گیری شود زاویه 90 درجه را نشان می دهد. به این زاویه زاویه راست یا قائمه می گویند.

زاویه $C$ زاویه راست یا قائمه است. یک زاویه راست 90 درجه است. به کمک گونیا می توان زاویه راست رسم کرد.

زاویه نیم صفحه: زاویه نیم صفحه شبیه به یک خط راست است و اگر با نقاله اندازه گیری شود اندازه آن 180 درجه می باشد. زاویه نیم صفحه به اندازه دو زاویه راست یعنی 180 درجه است.

نکته: زاویه های کمتر از نیم صفحه به سه دسته تقسیم می شوند:

1-به زاویه 90 درجه زاویه راست یا قائمه می گویند.

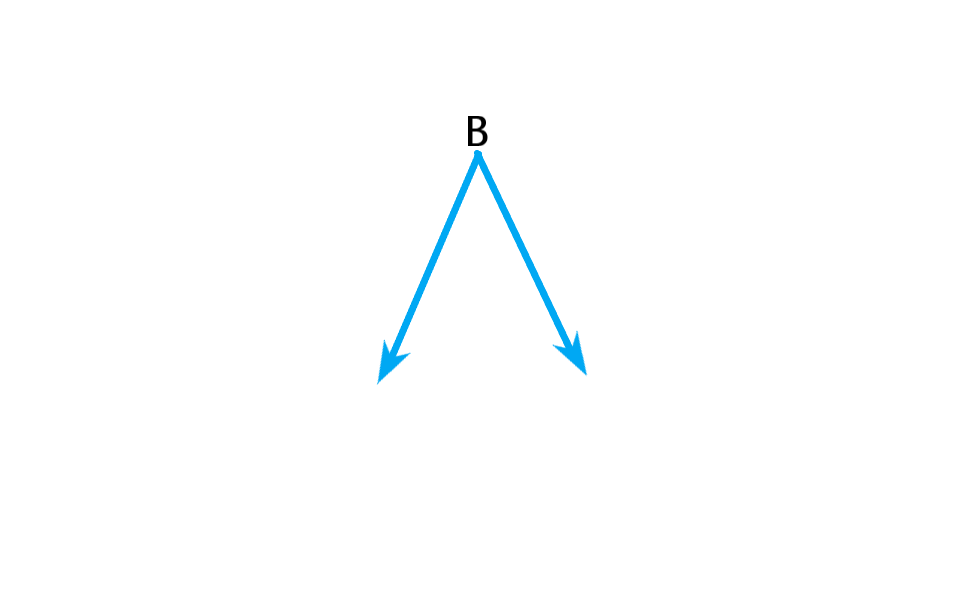
2-به زاویه هایی که از زاویه راست کوچکتر باشند، زاویه تند یا حاده می گویند. مثلا زاویه B زاویه تند است. زاویه های تند کمتر از 90 درجه هستند.

3-به زاویه هایی که از زاویه راست بزرگتر باشند و از زاویه نیم صفحه کوچکتر باشند، زاویه باز یا منفرجه می گویند. مثلا زاویه $A$ زاویه باز است. زاویه های باز بیشتر از 90درجه و کمتر از 180 درجه هستند.

دو زاویه چه روابطی می توانند با هم داشته باشند؟

در این بخش به برخی از روابطی که دو زاویه ممکن است با هم داشته باشند اشاره می شود:

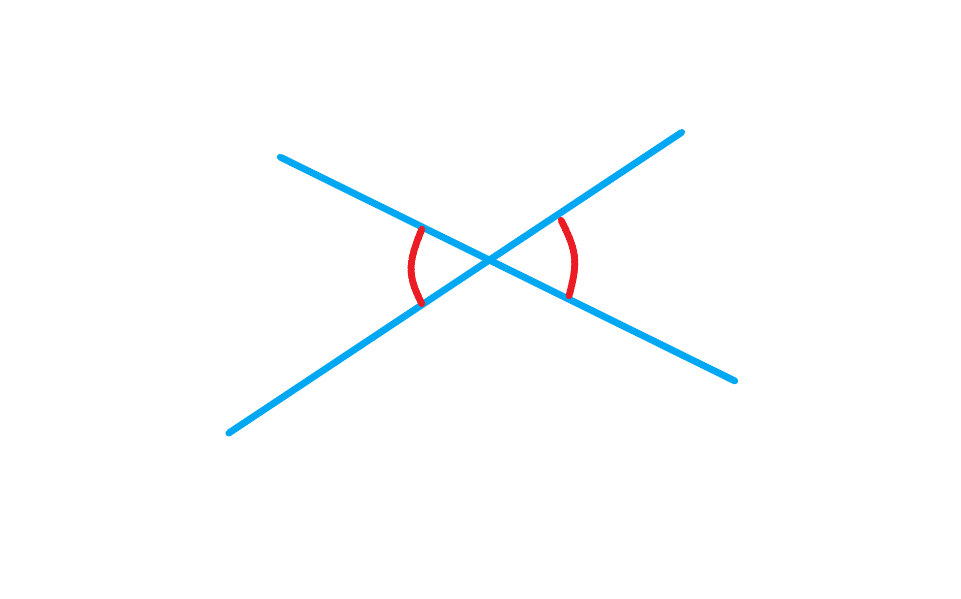
دو زاویه متقابل به راس: در شکل زیر دو زاویه متقابل به راس مشخص شدند. در واقع اگر راس دو زاویه برهم منطبق باشند و اضلاع این دو زاویه در امتداد یکدیگر باشند به این دو زاویه زوایای متقابل به راس می گویند. دو زاویه ی متقابل به راس همواره با هم برابرند.

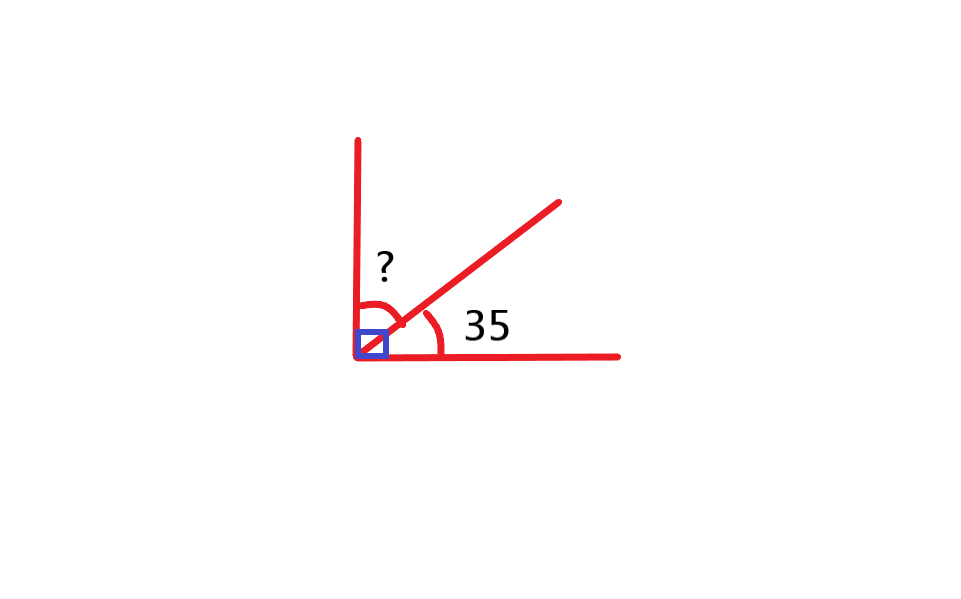
دو زاویه متمم: به هر دو زاویه که مجموع آنها 90 درجه باشد، دو زاویه متمم گویند.

مثلا در زاویه بالا برای اینکه زاویه مجهول را بدست آوریم باید به علامت مربع کنار زاویه بزرگتر توجه کنیم که نشان می دهد زاویه ی بزرگتر 90 درجه است. در نتیجه زاویه 35 درجه و زاویه مجهول متمم یکدیگرند. در نتیجه می توان نوشت:

$x+35=90$

$\rightarrow x=90-35=55$

$\rightarrow \,\,\, x=55$

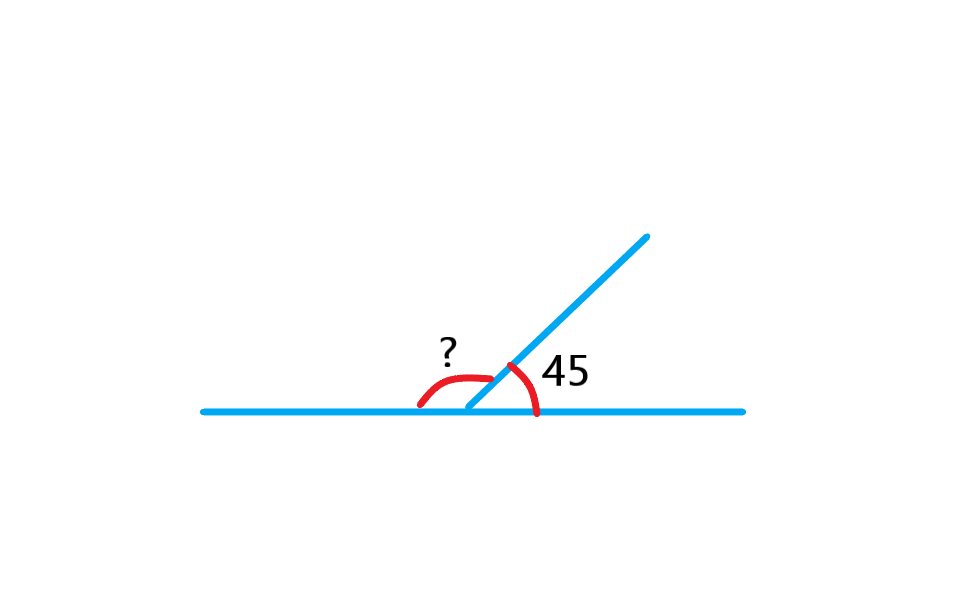
دو زاویه مکمل: به هر دو زاویه که مجموع آنها 180 درجه باشد، دو زاویه مکمل گویند.

در شکل بالا زاویه مجهول و زاویه 45 درجه با هم زاویه نیم صفحه که برابر با 180 درجه است می سازند. پس می توان گفت زاویه 45 درجه و زاویه مجهول مکمل یکدیگرند. در نتیجه می توان نوشت:

$x+45=180$

$\rightarrow x=180-45=135$

$\rightarrow \,\,\, x=135$

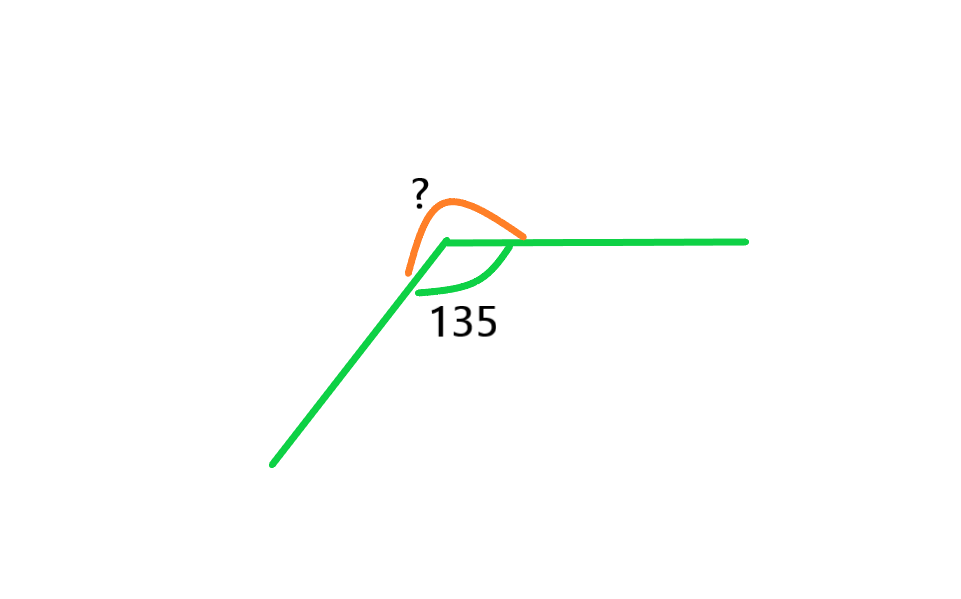
زاویه 360 درجه: یک دایره 360 درجه است بنابراین در شکل زیر می توان گفت که کل دایره 360 است و زاویه مجهول 135 درجه کمتر از این 360درجه است. داریم :

$x+135=360$

$\rightarrow x=360-135=225$

$\rightarrow \,\,\, x=225$

نیمساز یک زاویه چیست و چگونه بدست می آید؟

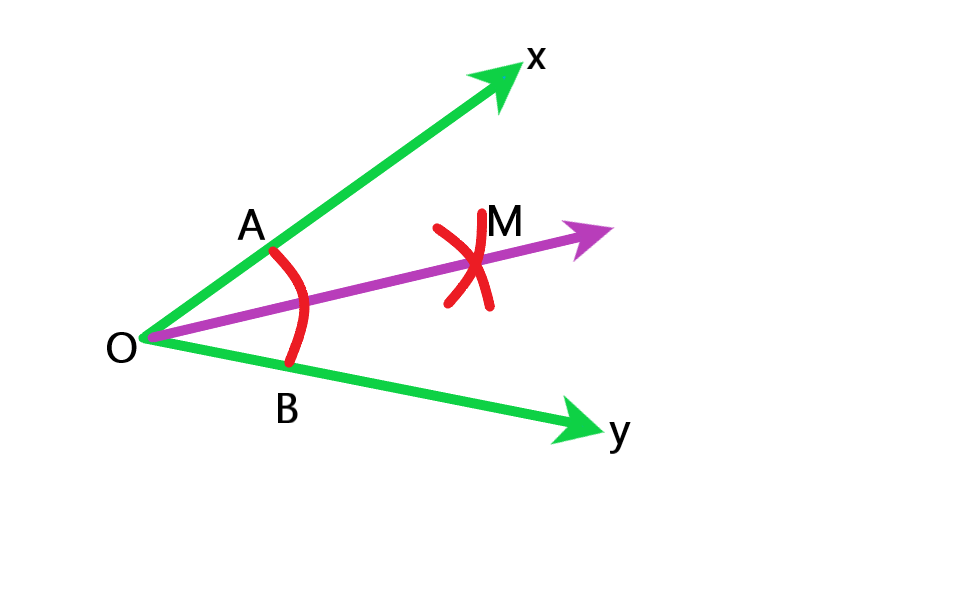
نیم خطی که زاویه را به دو زاویه ی مساوی تقسیم می کند نیمساز نامیده می شود.

برای رسم نیمساز یک زاویه مانند $xOy$ ابتدا سوزن پرگار را روی نقطه $O$ قرار می دهیم تا کمان اضلاع زاویه را در نقاط $A$ و $B$ قطع کند بعد دهانه پرگار را بیشتر از نصف $AB$ باز می کنیم و سوزن را روی $A$ می گذاریم و کمان می زنیم و یک بار دیگر همین کار را برای نقطه $B$ تکرار می کنیم محل برخورد دو کمان را به نقطه $O$ وصل می کنیم این خط همان نیمساز زاویه است. در نتیجه طبق $OM$ نیمساز زاویه $xOy$ است.

نکته: هر نقطه روی نیمساز زاویه از دو ضلع زاویه به یک فاصله است. و هر نقطه که از دو ضلع زاویه به یک فاصله باشد حتما روی نیمساز زاویه قرار می گیرد.

تعامد چیست؟ خطوط عمود برهم چه شرایطی دارند؟

تعامد (خطوط عمود بر هم): هرگاه دو خط با هم زاویه راست بسازند، می گوییم آن دو خط بر هم عمودند.

چند نکته درباره خطوط عمود بر هم:

در حالت کلی دو خط عمود بر یک خط با هم موازی اند.
عمود بودن خط $a$ بر $e$ را به صورت $a \perp e$ نشان می دهیم.
از یک نقطه خارج از یک خط نمی توان بیش از یک عمود بر آن خط رسم کرد.

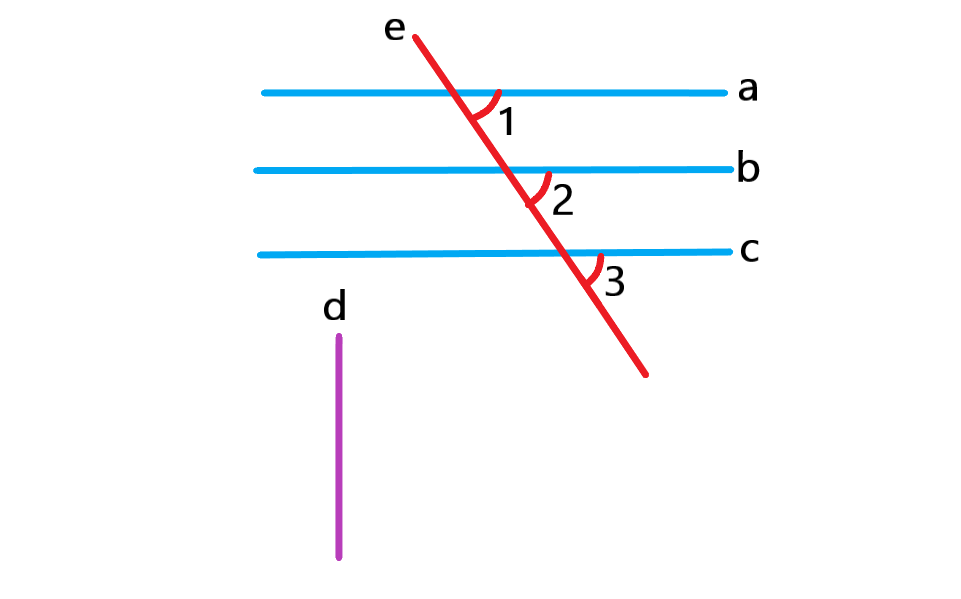
چه موقع دو خط با هم موازی اند؟

اگر زاویه 1 و 2 و 3 با هم برابر باشند آنگاه سه خط $a$ و $b$ و $c$ با هم موازی اند. و اگر سه خط با هم موازی باشند آنگاه سه زاویه 1 و 2 و 3 با هم برابرند. در واقع این عبارات یک گزاره ی دو شرطی هستند.

اگر خط $d$ بر یکی از خطوط $a$ یا $b$ یا $c$ عمود باشد بر دو خط دیگر هم عمود است به خط $e$ خط مورب می گویند.

توجه: موازی بودن دو خط $a$ و $b$ را به صورت $a \parallel b$ نشان می دهیم و موازی نبودن $b$ و $d$ را به صورت $b \nparallel d$ نشان می دهیم.

نکته: دو خط عمود بر یک خط با هم موازی اند. مثلا در اینجا $a$ و $b$ بر $d$ عمودند. پس با یکدیگر موازی اند.

نکته: اگر خطی بر یکی از دو خط موازی، عمود شود بر خط دوم هم عمود است. مثلا در شکل بالا $d$ بر $a$ عمود شده در حالی که $a$ و $b$ با هم موازی اند. پس می توان نتیجه گرفت که $d$ بر $b$ نیز عمود است.

نکته : دو خط موازی با یک خط خودشان با هم موازی اند. مثلا در شکل بالا اگر هم $a \parallel b$ و هم $c \parallel b$ پس می توان نتیجه گرفت $a \parallel c$ .

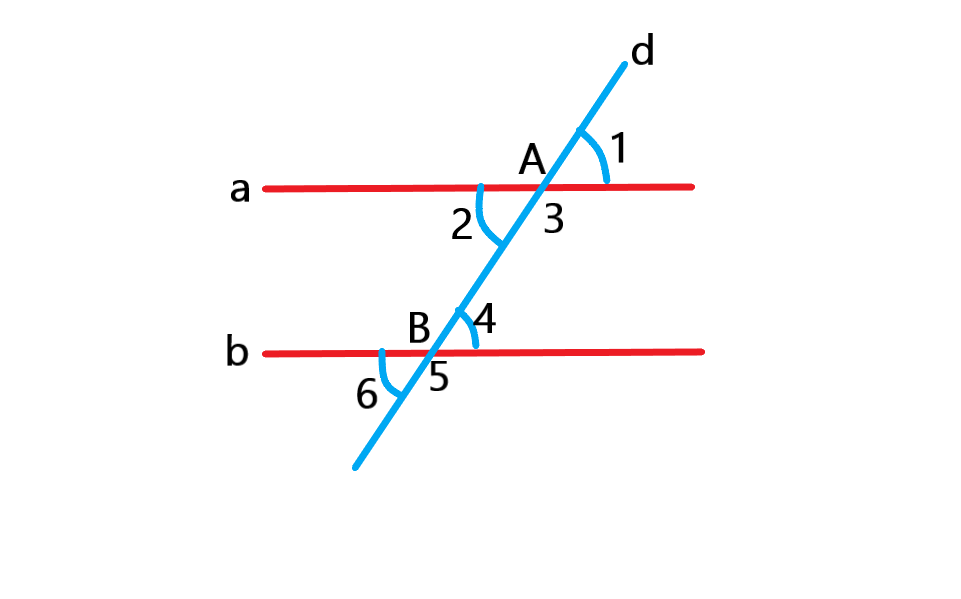
نکته: اگر خطی مانند $d$ خطوط $a$ و $b$ را با زاویه های مساوی قطع کند خطوط $a$ و $b$ با هم موازی هستند و $d$ مورب است.

در این حالت تساوی های زیر برقرارند:

$\hat{1}=\hat{2}=\hat{4}=\hat{6}\,\,\,,\,\,\,\hat{3}=\hat{5}$

به طور کلی هر گاه یک خط مورب دو خط موازی را قطع کند هشت زاویه ایجاد می کند که چهار تای آن ها تند و چهار تا باز هستند چهار زاویه تند با هم برابر هستند و چهار زاویه باز با هم برابر هستند. در این حالت هر زاویه تند مکمل هر زاویه باز می باشد.

توجه: در صورتی که خط مورب به صورت عمود باشد هر هشت زاویه برابر و قائمه هستند.

نکته: خطی که یکی از دو خط موازی را قطع کند حتما خط دوم را قطع می کند. مثلا اگر در شکل بالا می دانستیم که $d$ خط $a$ را قطع می کند و $a$ با $b$ موازی است می فهمیدیم اگر $d$ را به اندازه کافی امتداد دهیم، حتما $b$ را نیز قطع می کند.

نکته: از یک نقطه خارج یک خط فقط یک خط موازی با آن می توان رسم کرد.

نکته: مجموعه نقاطی که از یک خط مشخص مانند $d$ فاصله $h$ دارند دو خط موازی با خط $d$ در دو طرف این خط را تشکیل می دهند.

چه خطی عمودمنصف یک پاره خط است؟

عمود منصف خطی است که از وسط یک پاره خط بگذرد و بر آن عمود باشد.

هر نقطه روی عمودمنصف ِ یک پاره خط از دو سر آن پاره خط به یک فاصله است. و هر نقطه که از دو سر پاره خط به یک فاصله باشد حتما روی عمود منصف پاره خط قرار دارد. در شکل زیر $xy$ عمود منصف پاره خط $AB$ است.

چطور عمودمنصف یک پاره خط را رسم کنیم؟

برای رسم عمود منصف یک پاره خط باید پرگار را بیشتر از نصف طول پاره خط باز کنیم و سوزن پرگار را روی یک سر پاره خط بگذاریم و کمان بزنیم و یکبار دیگر برای سر دوم پاره خط تکرار می کنیم محل برخورد کمان ها دو نقطه هستند اگر این دو نقطه را به هم وصل کنیم عمود منصف پاره خط مذکور رسم می شود.

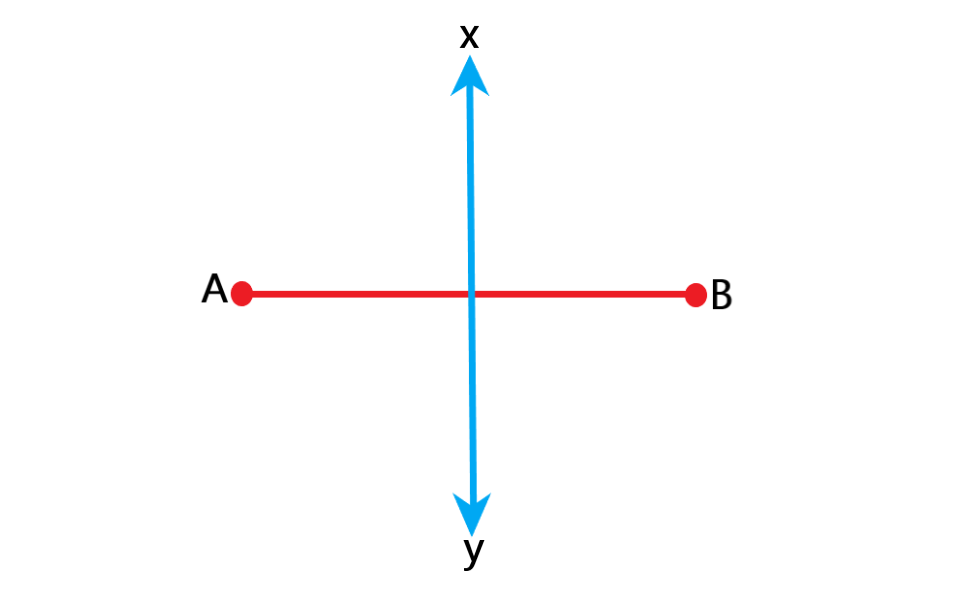
چطور فاصله دو نقطه را بدست آوریم؟

فاصله ی دو نقطه، طول کوتاهترین پاره خطی است که دو نقطه را به هم وصل می کند.

اگر $A$ و $B$ دو نقطه هم عرض در صفحه باشند آنگاه فاصله بین این دو نقطه برابر است با:

$AB=| x_{A} - x_{B} |$

اگر $C$ و $D$ دو نقطه هم طول در صفحه باشند آنگاه فاصله بین این دو نقطه برابر است با:

$CD=| y_{A}- y_{B}|$

به طور کلی فاصله دو نقطه $A(x_{A},y_{A})$ و $B(x_{B},y_{B})$ برابر است با:

$AB=\sqrt{( x_{A} - x_{B})^{2}+( y_{A}- y_{B})^{2}}$

مختصات نقطه وسط دو نقطه دلخواه را چگونه بدست آوریم؟

مختصات نقطه وسط دو نقطه $A(x_{A},y_{A})$ و $B(x_{B},y_{B})$ برابر است با :

$M(\frac{ x_{A}+ x_{B}}{2},\frac{ y_{A}+ y_{B}}{2})$

فاصله یک نقطه از یک خط چگونه بدست می آید؟

فاصله یک نقطه از یک خط، برابر طول پاره خطی است که از آن نقطه بر آن خط عمود می شود.

فاصله نقطه $A(x_{0},y_{0})$ از خط به معادله $ax+by+c=0$ برابر است با

$d=\frac{| ax_{0}+by_{0}+c | }{\sqrt{a^{2}+b^{2}}}$

صفحه چیست؟

صفحه از هر دو طرف ادامه دارد و ضخامتی ندارد.

نمایش صفحه: شکلهای مختلف نمایش صفحه عبارتند از صورت هایی که از اصول هندسه فضایی و تعریف دو خط موازی می توان نتیجه گرفت. این صورتها به شرح زیر هستند: ١-سه نقطه غیرواقع بر یک خط. ٢-یک خط و نقطه ای در خارج آن. ٣-دو خط متقاطع. 4- دو خط موازی

در واقع اگر سه نقطه غیر واقع بر یک خط داشته باشیم حتما یک صفحه از آن ها می گذرند.

اگر یک خط و یک نقطه خارج از آن داشته باشیم حتما یک صفحه از آن خط و نقطه می گذرد.

از دو خط متقاطع حتما یک صفحه می گذرد.

از دو خط موازی حتما یک صفحه می گذرد.

دو خط در فضا چه وضعیتی نسبت به هم می توانند داشته باشند؟

دو خط در فضا نسبت به هم یا متقاطع اند یا موازی اند یا متنافرند.

وقتی دو خط بر هم منطبق می شوند آنها را یک خط در نظر می گیریم.

اگر دو خط هیچ نقطه اشتراکی نداشته باشند و صفحه ای وجود داشته باشد که شامل هر دوی آنها باشد آن دو خط موازی اند.

اگر دو خط هیچ نقطه اشتراکی نداشته باشند و صفحه ای وجود نداشته باشد که شامل هر دوی آنها باشد آن دو خط متنافرند.

در یک صفحه دو خط موازی با یک خط با هم موازی اند.

در فضا دو خط موازی با یک خط با هم موازی اند.

در صفحه دو خط عمود بر یک خط با هم موازی اند.

نقطه و صفحه چه وضعیتی نسبت به هم می توانند داشته باشند؟

در این بخش وضعیت نقطه با خط، صفحه و فضا را بررسی می کنیم:

نکته: در صفحه از هر نقطه بی شمار خط می گذرد.

نکته: در فضا از هر نقطه بی شمار خط می گذرد.

اگر دو نقطه از خطی در صفحه ای باشد، تمام آن خط در آن صفحه قرار خواهد داشت.

از سه نقطه که روی یک خط راست نباشند یک و تنها یک صفحه می گذرد.

لاقل سه نقطه وجود دارد که بر یک خط راست واقع نیستند.
حداقل چهار نقطه وجود دارد که بر یک صفحه واقع نیستند.

خط نقطه صفحه و فضا چه وضعیتی نسبت به هم دارند؟

اصل پنجم اقلیدس: از هر نقطه فضا تنها یک خط موازی با خط مفروض می گذرد.

نکته: در صفحه از یک نقطه بیرون خط فقط یک خط می توان موازی با آن خط رسم کرد.

نکته: در فضا از یک نقطه بیرون خط فقط یک خط می توان موازی با آن خط رسم کرد.

نکته: از یک نقطه غیر واقع بر یک صفحه بیشمار خط موازی با صفحه می توان رسم کرد.

خط و صفحه چه وضعیتی نسبت به هم دارند؟

در این بخش به بررسی وضعیت خط و صفحه نسبت به هم در فضا را بررسی می کنیم:

نکته: اگر یک خط با یک صفحه متقاطع باشند خطوط صفحه نسبت به آن خط متقاطع یا متنافرند.

نکته: اگر خط و صفحه نسبت بهم هیچ نقطه اشتراکی نداشته باشند نسبت بهم موازی اند.

نکته: اگر خط و صفحه در یک نقطه مشترک باشند نسبت بهم متقاطع اند.

نکته: اگر خط و صفحه بیشمار نقطه مشترک داشته باشند خط بر صفحه واقع است.

نکته: از یک خط در فضا بیشمار صفحه می گذرد.

نکته: از دو خط متقاطع فقط یک صفحه می گذرد.

نکته: از دو خط موازی فقط یک صفحه می گذرد.

نکته: اگر دو خط در فضا با هم موازی باشد و یک صفحه با یکی از این خطوط موازی باشد خط دوم ممکن است روی اسن صفحه باشد یا ممکن است با این صفحه موازی باشد.

نکته: اگر دو خط در فضا با هم موازی باشد و یک صفحه شامل یکی از این خطوط باشد یا شامل خط دوم هم هست یا موازی با آن است.

نکته: اگر دو خط در فضا با هم موازی باشد و یک صفحه با یکی از این خطوط متقاطع باشد نسبت به خط دوم هم متقاطع است.

نکته: اگر دو خط در فضا با هم متنافر باشند و یک صفحه با یکی از این خطوط موازی باشد صفحه ممکن است شامل خط دوم باشد یا موازی یا متقاطع با خط دوم باشد.

نکته: اگر دو خط در فضا با هم متنافر باشند و یک صفحه شامل یکی از این خطوط باشد یا شامل خط دوم هم هست یا متقاطع با آن است.

نکته: اگر دو خط در فضا با هم متنافر باشند و یک صفحه با یکی از این خطوط متقاطع باشد ممکن است نسبت به خط دوم هم متقاطع باشد یا با خط دوم موازی باشد یا شامل آن باشد.

نکته: خط و صفحه در فضا نسبت به هم یا متقاطع اند یا موازی یا خط بر صفحه واقع است.

نکته: اگر دو صفحه متمایز یک نقطه مشترک داشته باشند در یک خط راست مشترک خواهند بود.

دو صفحه چه وضعیتی نسبت به هم دارند؟

در این بخش به بررسی وضعیت دو صفحه نسبت به هم در فضا می پردازیم:

نکته: اگر دو صفحه با هم نقطه اشتراکی نداشته باشند نسبت بهم موازی اند.

نکته: اگر دو صفحه در یک خط راست مشترک باشند نسبت به هم متقاطع اند خط راستی که اشتراک دو صفحه متقاطع است فصل مشترک آن دو صفحه نامیده می شود.

نکته: دو صفحه در فضا موازی یا متقاطع اند وقتی دو صفحه بر هم منطبق می شوند آنها را یک صفحه در نظر می گیریم.

چه خطی بر یک صفحه عمود است؟

تعریف: فرض کنید خط $L$ در نقطه $A$ صفحه $P$ را قطع می کند. خط $L$ بر صفحه $P$ عمود است هرگاه بر تمام خطوط صفحه $P$ که از نقطه A می گذرند عمود باشد.

نکته: اگر خطی بر دو خط متقاطع از صفحه ای در محل تقاطع عمود باشد بر آن صفحه عمود است.

نکته: اگر خطی بر یک خط از صفحه عمود باشد الزاما بر صفحه عمود نیست.

تعریف: دو صفحه بر هم عمودند هرگاه هر کدام شامل خطی باشد که بر دیگری عمود است.

نکته: دو خط عمود بر یک صفحه همیشه با هم موازی اند.

نکته: دو صفحه عمود بر یک صفحه الزاما با هم موازی نیستند. ممکن است بر هم عمود باشند.

نکته: دو صفحه عمود بر یک خط با هم موازی اند.

نکته: اگر خطی بر یکی از دو صفحه موازی عمود باشد بر صفحه دوم هم عمود است.

جمع بندی

در این مقاله به توضیح مفصلی در مورد انواع خطوط، انواع زاویه، روابط زوایا با همدیگر پرداختیم. همچنین نیمساز، عمودمنصف خطوط موازی و خطوط عمود بر هم را بررسی کردیم. فرمول های فاصله بین دو نقطه و فاصله یک نقطه از خط را بیان کردیم. به بیان وضعیت بین دو خط بین دو صفحه و بین یک خط و یک صفحه پرداختیم. این مقاله توضیح کاملی درباره ی هندسه تحلیلی و همه ی زیرمجموعه های آن است. اگر علاقمند به دانستن اطلاعاتی در مورد رسم عمودمنصف و نیمساز هستید حتما به مقاله مکان هندسی مراجعه کنید. اگر می خواهید بدانید معادله یک خط چطور بدست می آید که بتوان فاصله هر نقطه دلخواه از خط مورد نظر را پیدا کنید حتما به مقاله تابع خطی مراجعه کنید. لطفا ما را از نظرات ارزشمند خود درباره مقاله هندسه تحلیلی در قسمت کامنت ها بهره مند کنید.

جامع ترین آموزش در حوزه هندسه تحلیلی، خط، نقطه، زاویه صفحه و فضا

هندسه ترسیمی چیست؟

خطوط چند دسته اند؟

زاویه چیست و چه انواعی دارد؟

دو زاویه چه روابطی می توانند با هم داشته باشند؟

نیمساز یک زاویه چیست و چگونه بدست می آید؟

تعامد چیست؟ خطوط عمود برهم چه شرایطی دارند؟

چه موقع دو خط با هم موازی اند؟

چه خطی عمودمنصف یک پاره خط است؟

چطور عمودمنصف یک پاره خط را رسم کنیم؟

چطور فاصله دو نقطه را بدست آوریم؟

مختصات نقطه وسط دو نقطه دلخواه را چگونه بدست آوریم؟

فاصله یک نقطه از یک خط چگونه بدست می آید؟

صفحه چیست؟

دو خط در فضا چه وضعیتی نسبت به هم می توانند داشته باشند؟

نقطه و صفحه چه وضعیتی نسبت به هم می توانند داشته باشند؟

خط نقطه صفحه و فضا چه وضعیتی نسبت به هم دارند؟

خط و صفحه چه وضعیتی نسبت به هم دارند؟

دو صفحه چه وضعیتی نسبت به هم دارند؟

چه خطی بر یک صفحه عمود است؟

دیدگاهتان را بنویسید لغو پاسخ

آخرین مطالب وبلاگ

دنباله های عددی

تابع خطی و معادله خط

تابع و دامنه و برد آن

تعیین علامت

عبارت و معادله گویا

معادله درجه دوم

معادله

عبارت جبری

قدرمطلق

دوره ها

دسترسی سریع

دسترسی سریع

مقالات مادر