کامل ترین آموزش در باب مساحت و محیط اشکال هندسی در صفحه

مساحت و محیط هر شکل هندسی به ترتیب نشان دهنده سطحی که آن شکل هندسی اشغال می کند و اندازه دور آن شکل هندسی است. در این مقاله به آموزش مساحت و محیط شکل های هندسی مختلف می پردازیم از جمله دایره، مثلث،همچنین چهارضلعی هایی مانند مربع ، لوزی ، مستطیل ، متوازی الاضلاع و ذوزنقه. در آخر مقاله را با آموزش نقاط شبکه ای و بیان ارتباط آن با مساحت به پایان می رسانیم.

مساحت و محیط دایره

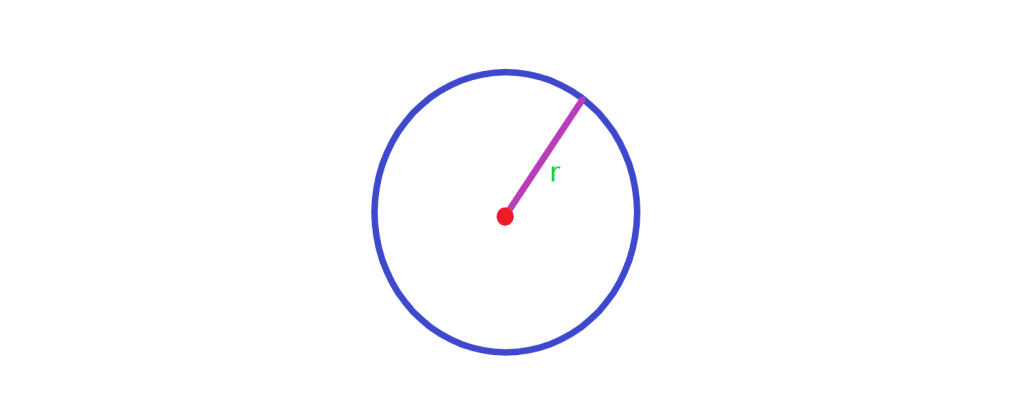
دایره یک شکل هندسی به صورت زیر است که محیط و مساحت آن بر حسب شعاع آن بدست می آید. اگر علاقمند به اطلاعات بیشتری درباره ی دایره هستید لطفا به مقاله مربوطه مراجعه فرمایید.

محیط دایره به شعاع $r$ برابر حاصلضرب دو برابر شعاع در عدد پی است. $P=2r\pi$

مساحت دایره به شعاع $r$ برابر حاصلضرب شعاع در شعاع در عدد پی است. $S=\pi r^{2}$

مساحت و محیط مثلث

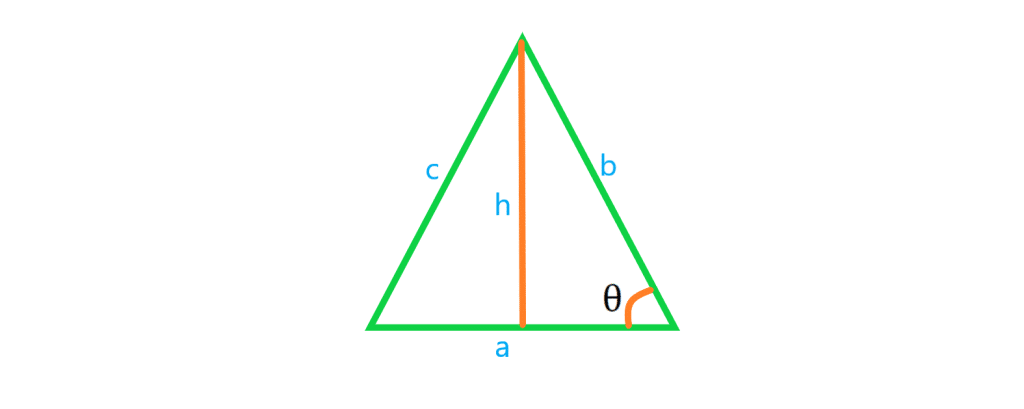
همانطور که در مقاله مثلث خواندیم به هر سه ضلعی بسته، مثلث می گویند. در حالت کلی مساحت مثلث برابر نصف حاصلضرب ارتفاع مثلث $(h)$ در قاعده ی نظیرش $a$ است. $S=\frac{ha}{2}$ و محیط مثلث برابر مجموع اندازه سه ضلع آن است. $P=a+b+c$

البته مساحت مثلث را با کمک مثلثات می توان از رابطه ی $S=\frac{ab\sin\theta}{2}$ نیز بدست آورد.

همچنین در مقاله مثلث روش هرون را می خوانیم.

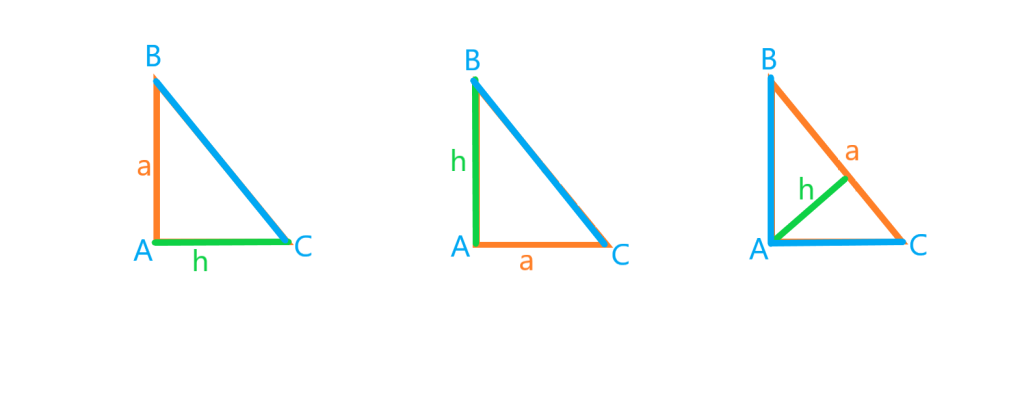
در مثلث قائم الزاویه به سه حالت می توان ارتفاع رسم کرد که دو حالت از آن ارتفاع یکی از اضلاع مثلث است. در هر سه حالت $S=\frac{ha}{2}$ می باشد. این سه حالت را در شکل زیر می توان دید:

در هر مثلث متساوی الاضلاع به ضلع دلخواه $a$ اندازه ارتفاع رادیکال سه دوم ضلع یعنی $\frac{\sqrt{3}}{2} a$ و اندازه مساحت برابر $\frac{\sqrt{3}}{4} a^{2}$ است.

نکته: در دو مثلث اگر اندازه قاعده ها با هم برابر باشند نسبت مساحت ها برابر نسبت اندازه ارتفاع های متناظر با این دو قاعده است.

نکته: در دو مثلث که اندازه دو ارتفاع برابر باشد نسبت مساحت ها برابر نسبت اندازه های قاعده های متناظر با این دو ارتفاع است.

نکته: اگر وسط های سه ضلع هر مثلث را به هم متصل کنیم چهار مثلث هم نهشت و درنتیجه هم مساحت هستند.

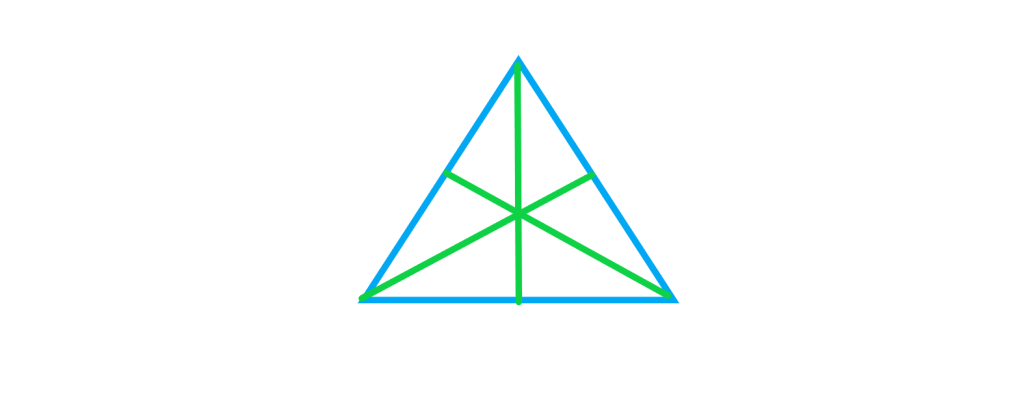
نکته: میانه های هر مثلث آن را به شش قسمت با مساحت های برابر تقسیم می کند.

نکته: اگر دو مثلث در یک راس مشترک بوده و قاعده مقابل به این راس آنها روی یک خط راست باشد نسبت مساحت های آنها برابر با نسبت اندازه قاعده های آنهاست. چون ارتفاع هایشان برابرند.

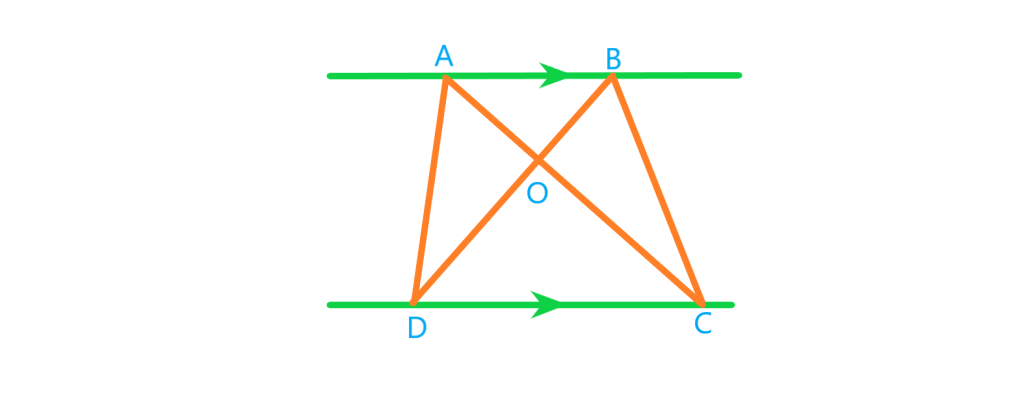
نکته: اگر دو مثلث قاعده مشترکی داشته باشند و راس های روبرو این قاعده آنها روی یک خط موازی باشند این مثلث ها هم مساحت اند (مساحت هایشان با هم برابر است).

نکته: فرض کنیم دو خط $AB$ و $CD$ موازی باشند به طوری که دو خط $AC$ و $BD$ در نقطه ای مانند $O$ متقاطع باشند می توان نتیجه گرفت :

$S_{ADC}=S_{BCD}\,\,\, ,\,\,\, S_{OAD}=S_{OBC}$

مساحت و محیط مربع

مربع یک چهارضلعی با ضلع ها و زاویه های برابر است. اگر علاقمند به دانستن مطالب بیشتری راجع به مربع هستید لطفا به مقاله چندضلعی ها مراجعه کنید. مساحت مربع برابر مجذور اندازه یک ضلع آن است. یعنی مساحت مربع به ضلع $a$ برابر $S=a^{2}$ است.

مساحت مربعی به ضلع یک سانتی متر برابر با یک سانتی متر مربع است.

محیط مربع به ضلع $a$ برابر $P=4a$ است.

مساحت و محیط لوزی

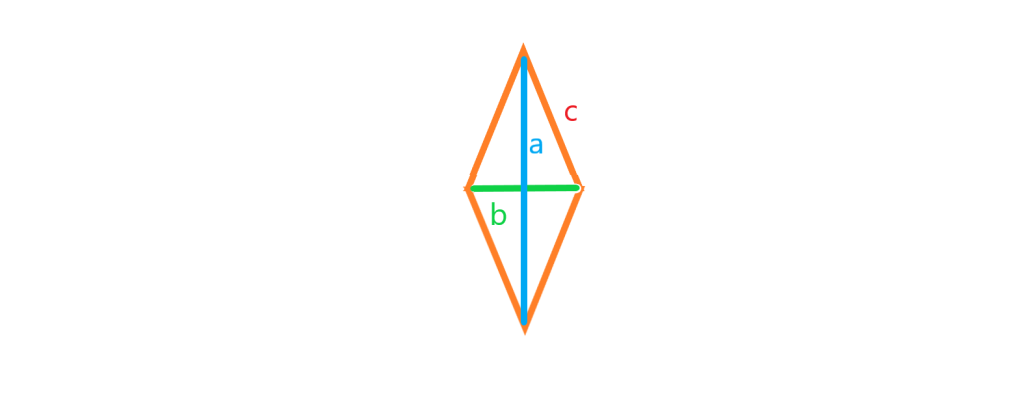
لوزی یک چهارضلعی با اضلاع برابر است. اگر علاقمند به دانستن مطالب بیشتری راجع به لوزی هستید لطفا به مقاله چندضلعی ها مراجعه کنید. مساحت مربع برابر مجذور اندازه یک ضلع آن است. یعنی مساحت لوزی برابر نصف حاصل ضرب قطرهاش هست یعنی مساحت لوزی به قطر $a$ و $b$ برابر $S=\frac{ab}{2}$ است.

محیط لوزی به ضلع $c$ برابر $P=4c$ است.

نکته: به طور کلی در هر چهارضلعی با قطرهای عمود بر هم، مساحت برابر با نصف حاصل ضرب قطرهاست.

مساحت و محیط مستطیل

مستطیل یک چهارضلعی با زاویه های برابر است. اگر علاقمند به دانستن مطالب بیشتری راجع به مستطیل هستید لطفا به مقاله چندضلعی ها مراجعه کنید. با رسم قطر مستطیل دو مثلث با مساحت های برابر بدست می آید.

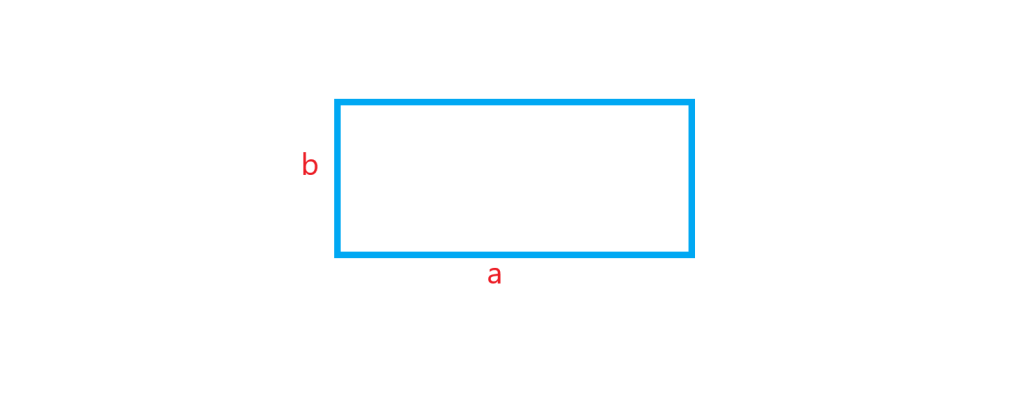
مساحت مستطیل برابر حاصلضرب طول در عرض آن است .

$S=ab$

محیط مستطیل برابر است با مجموع اندازه ی هر چهارضلع که چون اضلاع روبرو دو به دو با هم برابرند می توان نوشت

$P=2(a+b)$

مساحت و محیط متوازی الاضلاع

متوازی الاضلاع یک چهارضلعی است که ضلع های روبرویش دو به دو با هم موازی اند. اگر علاقمند به دانستن مطالب بیشتری راجع به متوازی الاضلاع هستید لطفا به مقاله چندضلعی ها مراجعه کنید.

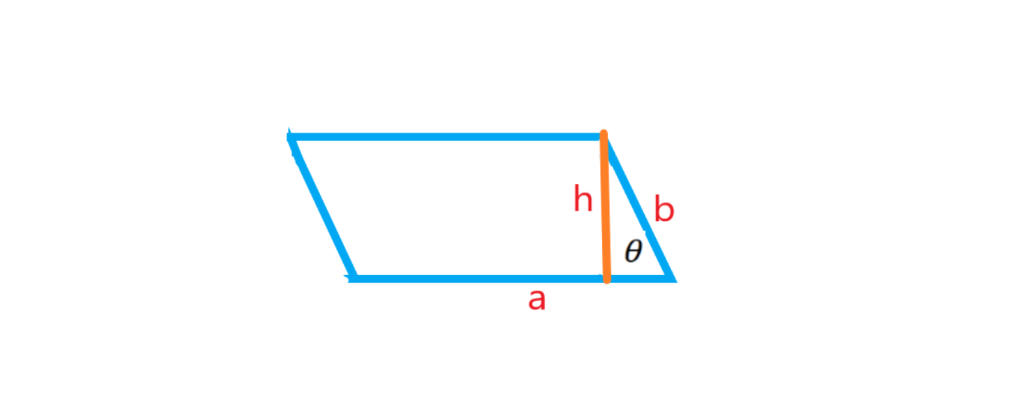
مساحت متوازی الاضلاع برابر حاصل ضرب اندازه ارتفاع در قاعده آن است.

$S=ha$

نکته : مساحت هر متوازی الاضلاع برابر است با حاصل ضرب دو ضلع مجاور در سینوس زاویه بین آن دو ضلع . $S=ab \sin \theta$ ( برای یادگیری سینوس زاویه های مختلف به مقاله معرفی نسبت های مثلثاتی مراجعه کنید)

محیط متوازی الاضلاع برابر است با مجموع اندازه ی هر چهارضلع که چون اضلاع روبرو دو به دو با هم برابرند می توان نوشت

$P=2(a+b)$

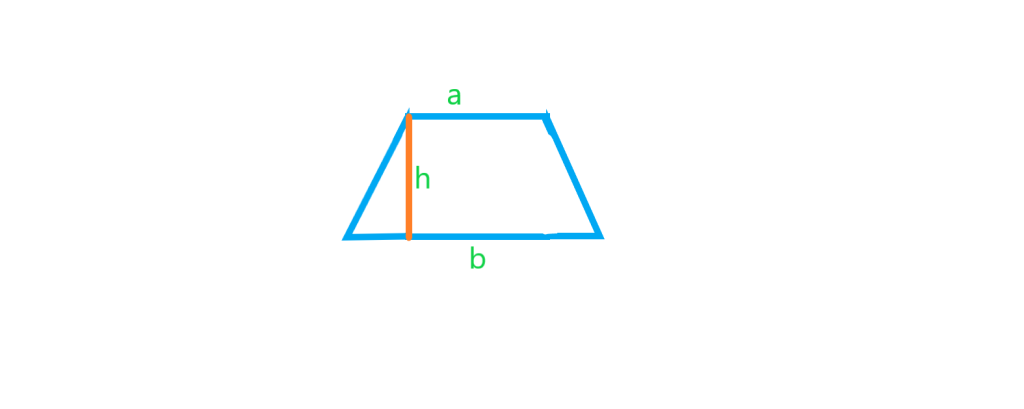
مساحت و محیط ذوزنقه

ذوزنقه یک چهارضلعی با فقط دو ضلع موازی است. اگر علاقمند به دانستن مطالب بیشتری راجع به ذوزنقه هستید لطفا به مقاله چندضلعی ها مراجعه کنید.

مساحت ذوزنقه برابر نصف حاصلضرب مجموع دو قاعده در ارتفاع یعنی برابر است با $S=\frac{h(a+b)}{2}$

محیط ذوزنقه برابر با حاصل جمع همه ی چهار ضلع آن است.

نقاط شبکه ای و مساحت

اگر صفحه را با خطوط موازی افقی و عمودی که به انaدازه واحد از هم فاصله دارند پر کنیم و محل برخورد خطوط افقی و عمود را نقطه شبکه ای در نظر بگیریم به چندضلعی هایی که تمام راس هایشان روی این نقاط قرار می گیرند چندضلعی شبکه ای می گویند.

نقاط مرزی شبکه ای: نقاط شبکه ای روی راس ها و ضلع های چندضلعی را نقاط مرزی شبکه ای می گویند. تعداد نقاط مرزی شبکه ای را با $b$ نشان می دهند.

نقاط درونی شبکه ای: نقاط شبکه ای درون چندضلعی ها را نقاط درونی شبکه ای برای چندضلعی می گویند. تعداد نقاط درونی شبکه ای را با $i$ نشان می دهند.

نکته: برای رسم یک چندضلعی شبکه ای حداقل به سه نقطه مرزی نیاز داریم.

نکته:: برای رسم یک چندضلعی شبکه ای حداقل به صفر نقطه درونی نیاز داریم.

نکته: مساحت چند ضلعی های شبکه ای به صورت $S=\frac{b}{2}-1+i$ بدست می آید.

نکته: در هر مربع شبکه ای مساحت صحیح و مثبت است.

نکته: هیچ مثلث متساوی الاضلاعی وجود ندارد که مختصات تمام راس هایش اعداد صحیح باشند.

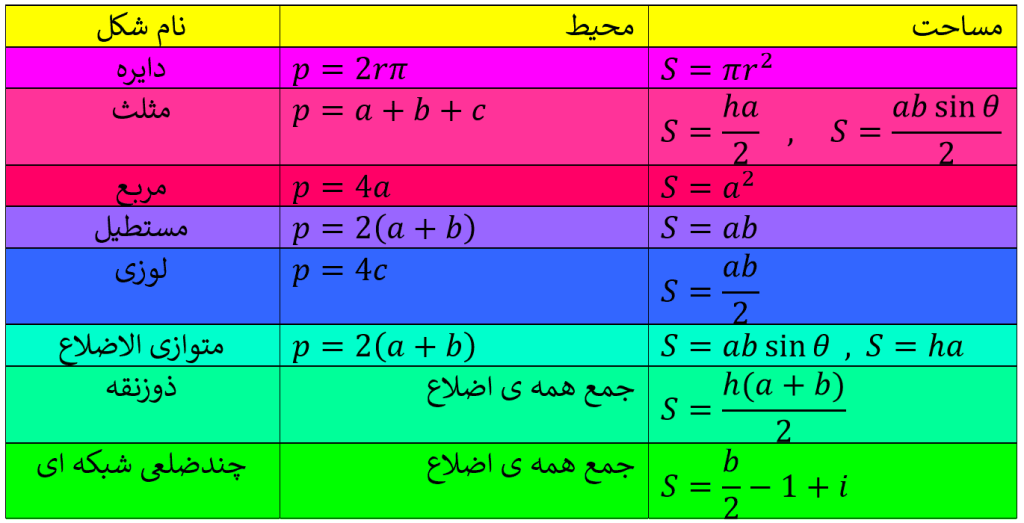
نکات این مقاله را به صورت خلاصه می توانید در جدول زیر ببینید:

جمع بندی

در این مقاله به آموزش مساحت و محیط اشکال هندسی مانند دایره، مثلث و چندضلعی ها (شامل متوازی الاضلاع، مربع، ذوزنقه، مستطیل و لوزی) پرداختیم. متوجه شدیم با این که تعریف محیط اندازه دور شکل است می توان برای بعضی از اشکال فرمولی برای محیط تعریف کرد. مساحت برخی اشکال هندسی مانند مثلث و متوازی الاضلاع دو فرمول دارد که همه ی این مباحث را با رسم اشکال هندسی مناسب در مقاله محیط و مساحت بیان کردیم و در آخر به تعریف نقاط شبکه ای و رابطه آن با مساحت پرداختیم. لطفا نظرات خود را درباره ی مقاله محیط و مساحت در قسمت کامنت ها بیان کنید.

کامل ترین آموزش در باب مساحت و محیط اشکال هندسی در صفحه

مساحت و محیط دایره

مساحت و محیط مثلث

مساحت و محیط مربع

مساحت و محیط لوزی

مساحت و محیط مستطیل

مساحت و محیط متوازی الاضلاع

مساحت و محیط ذوزنقه

نقاط شبکه ای و مساحت

دیدگاهتان را بنویسید لغو پاسخ

آخرین مطالب وبلاگ

دنباله های عددی

تابع خطی و معادله خط

تابع و دامنه و برد آن

تعیین علامت

عبارت و معادله گویا

معادله درجه دوم

معادله

عبارت جبری

قدرمطلق

دوره ها

دسترسی سریع

دسترسی سریع

مقالات مادر