آموزش جامع صفحه مختصات و نقاط روی آن

صفحه مختصات یک صفحه قرارداری است که از چهار ناحیه تشکل شده است. این چهار ناحیه توسط دو خط عمود برهم که به محور افقی محور طول و به محور عمودی که بر محور افقی عمود است محور عرض می گویند در این مقاله به آموزش مختصات می پردازیم. در این مقاله یاد می گیریم که چطور به هر نقطه در صفحه یک مختصات نسبت دهیم، چطور قرینه هر نقطه نسبت به محور طول ، نسبت به محور عرض و نسبت به مبدا مختصات بدست آوریم.

دستگاه مختصات و چهار ناحیه آن

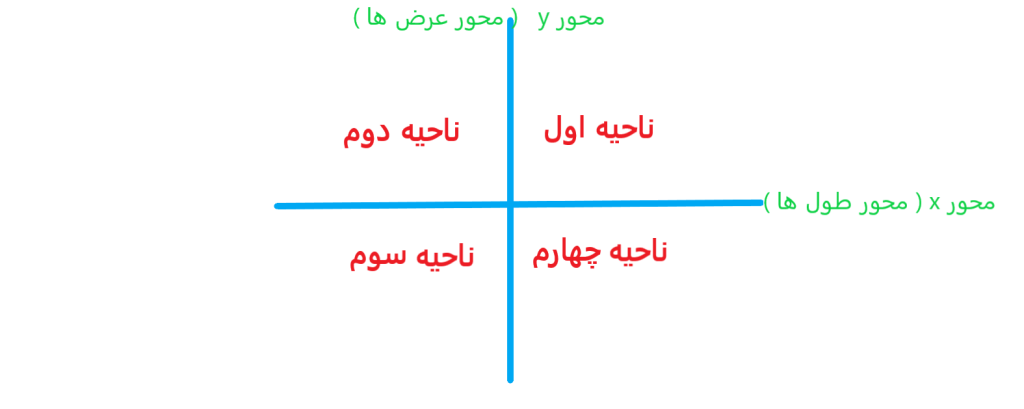
صفحه مختصات از دو محور افقی (محور طول) و عمودی(محور عرض) تشکیل شده است. محور های مختصات صفحه را به چهار قسمت مطابق شکل زیر تقسیم می کنند.

اگر از نقطه ای که می خواهیم مختصات آن را بدست آوریم بر محور طول ها عمودی رسم کنیم نقطه ای روی محور طول ایجاد می شود که نشان دهنده ی عدد $x$ است. اگر از نقطه موردنظر بر محور عرض ها عمودی رسم کنیم نقطه ای روی محور عرض ایجاد می شود که نشان دهنده ی عدد است. در اینصورت می توان مختصات نقطه مورد نظر را به صورت $\begin{bmatrix} x \\ y \end{bmatrix}$ نشان داده می شود.

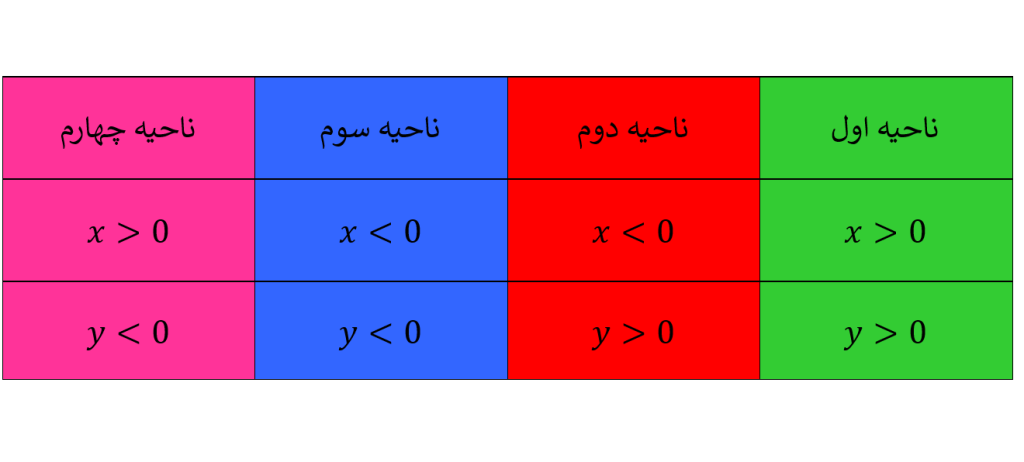
توجه1: در ناحیه اول هم مقدار طول و هم مقدار عرض هر نقطه مثبت است. یعنی $x > 0 , y > 0$

توجه2: در ناحیه دوم مقدار طول هر نقطه منفی و مقدار عرض هر نقطه مثبت است. یعنی $x < 0 , y > 0$

توجه3: در ناحیه سوم هم مقدار طول و هم مقدار عرض هر نقطه منفی است. یعنی $x < 0 , y < 0$

توجه4: در ناحیه چهارم مقدار طول هر نقطه مثبت و مقدار عرض هر نقطه منفی است. یعنی $x > 0 , y < 0$ .

به طور کلی می توان گفت:

مختصات یک نقطه در صفحه مختصات چگونه بدست می آید؟

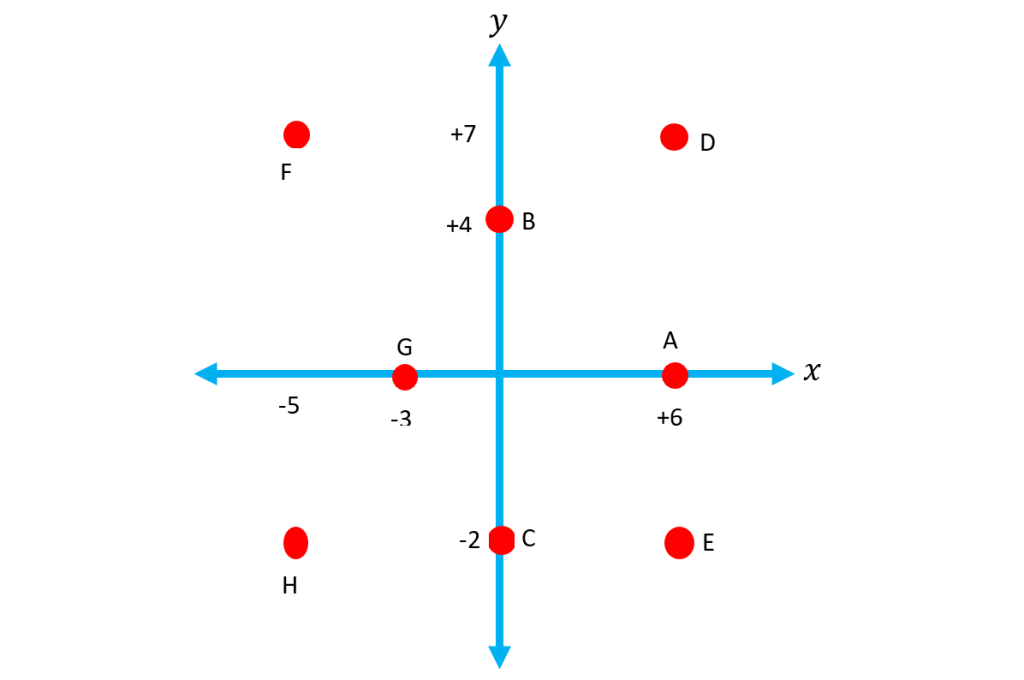
برای اینکه متوجه شوید مختصات هر نقطه چطور بدست می آید صفحه مختصات زیر را در نظر بگیرید. در این صفحه مختصات هشت نقطه مشخص شده چهار نقطه در چهار ناحیه قرار دارند و چهار نقطه در نقاط مرزی بین ناحیه ها. مختصات این هشت نقطه به صورت زیر بدست می آید:

$D=\begin{bmatrix} +6 \\ +7 \end{bmatrix} \,\,\, ,\,\,\, E=\begin{bmatrix} +6 \\ -2 \end{bmatrix}$

$F=\begin{bmatrix} -5 \\ +7 \end{bmatrix} \,\,\, ,\,\,\, H=\begin{bmatrix} -5 \\ -2 \end{bmatrix}$

$A=\begin{bmatrix} +6 \\ 0 \end{bmatrix} \,\,\, ,\,\,\, B=\begin{bmatrix} 0 \\ +4 \end{bmatrix}$

$C=\begin{bmatrix} 0 \\ -2 \end{bmatrix} \,\,\, ,\,\,\, G=\begin{bmatrix} -3 \\ 0 \end{bmatrix}$

می بینیم که $A$ بین ناحیه اول و چهارم قرار دارد. در نتیجه مقدار عرض آن صفر است و مقدار طول آن مثبت است. نقطه $B$ بین ناحیه اول و دوم قرار دارد. در نتیجه مقدرا طول آن صفر است و مقدار عرض آن یک عدد مثبت است. نقطه $G$ بین ناحیه دوم و سوم قرار دارد. در نتیجه مقدرا عرض آن صفر است و مقدار طول آن یک عدد منفی است. نقطه $C$ بین ناحیه سوم و چهارم قرار دارد. در نتیجه مقدار طول آن صفر است و مقدار عرض آن منفی است.

نقطه $D$ در ناحیه اول قرار دارد در نتیجه مقدار طول و عرض آن مثبت است. نقطه $F$ در ناحیه دوم قرار دارد در نتیجه مقدار طول آن منفی است و مقدار عرض آن مثبت است. نقطه $H$ در ناحیه سوم قرار دارد در نتیجه مقدار طول و عرض آن منفی است. نقطه $E$ در ناحیه چهارم قرار دارد در نتیجه مقدرا طول آن مثبت و مقدار عرض آن منفی است.

چطور قرینه یک نقطه را نسبت به محورهای مختصات و مبدا آن بدست آوریم؟

برای اینکه قرینه یک نقطه نسبت به محور طول ها را بدست آوریم باید عرض آن را قرینه کنیم.

مثلا قرینه نقاط $D=\begin{bmatrix} +6 \\ +7 \end{bmatrix} \, ,\,\, E=\begin{bmatrix} +6 \\ -2 \end{bmatrix}\, ,\,\, F=\begin{bmatrix} -5 \\ +7 \end{bmatrix}\, ,\,\, H=\begin{bmatrix} -5 \\ -2 \end{bmatrix}$ نسبت به محور طولها برابر است با

$D^{'}=\begin{bmatrix} +6 \\ -7 \end{bmatrix} \, ,\,\, E^{'}=\begin{bmatrix} +6 \\ +2 \end{bmatrix}$

$F^{'}=\begin{bmatrix} -5 \\ -7 \end{bmatrix} \, ,\,\, H^{'}=\begin{bmatrix} -5 \\ +2 \end{bmatrix}$

قرینه نقاط $A=\begin{bmatrix} +6 \\ 0 \end{bmatrix} \, ,\,\, B=\begin{bmatrix} 0 \\ +4 \end{bmatrix} \, ,\,\, C=\begin{bmatrix} 0 \\ -2 \end{bmatrix} \, ,\,\, G=\begin{bmatrix} -3 \\ 0 \end{bmatrix}$ نسبت به محور طول ها برابر است با

$A^{'}=\begin{bmatrix} +6 \\ 0 \end{bmatrix} \, ,\,\, B^{'}=\begin{bmatrix} 0 \\ -4 \end{bmatrix}$

$C^{'}=\begin{bmatrix} 0 \\ +2 \end{bmatrix} \, ,\,\, G^{'}=\begin{bmatrix} -3 \\ 0 \end{bmatrix}$

برای اینکه قرینه یک نقطه نسبت به محور عرض ها را بدست آوریم باید طول آن را قرینه کنیم.

مثلا قرینه نقاط $D=\begin{bmatrix} +6 \\ +7 \end{bmatrix} \, ,\,\, E=\begin{bmatrix} +6 \\ -2 \end{bmatrix} \, ,\,\, F=\begin{bmatrix} -5 \\ +7 \end{bmatrix} \, ,\,\, H=\begin{bmatrix} -5 \\ -2 \end{bmatrix}$ نسبت به محور عرضها برابر است با

$D^{'}=\begin{bmatrix} -6 \\ +7 \end{bmatrix} \, ,\,\, E^{'}=\begin{bmatrix} -6 \\ -2 \end{bmatrix}$

$F^{'}=\begin{bmatrix} +5 \\ +7 \end{bmatrix} \, , \,\, H^{'}=\begin{bmatrix} +5 \\ -2 \end{bmatrix}$

قرینه نقاط $A=\begin{bmatrix} +6 \\ 0 \end{bmatrix} \, ,\,\, B=\begin{bmatrix} 0 \\ +4 \end{bmatrix} \, ,\,\, C=\begin{bmatrix} 0 \\ -2 \end{bmatrix} \, , \,\, G=\begin{bmatrix} -3 \\ 0 \end{bmatrix}$ نسبت به محور عرض ها برابر است با

$A^{'}=\begin{bmatrix} -6 \\ 0 \end{bmatrix} \, , \,\, B^{'}=\begin{bmatrix} 0 \\ +4 \end{bmatrix}$

$C^{'}=\begin{bmatrix} 0 \\ -2 \end{bmatrix} \, , \,\, G^{'}=\begin{bmatrix} +3 \\ 0 \end{bmatrix}$

برای اینکه قرینه یک نقطه نسبت به مبدا مختصات را بدست آوریم باید طول و عرض آن را قرینه کنیم.

مثلا قرینه نقاط $D=\begin{bmatrix} +6 \\ +7 \end{bmatrix} \, ,\,\, E=\begin{bmatrix} +6 \\ -2 \end{bmatrix} \, ,\,\, F=\begin{bmatrix} -5 \\ +7 \end{bmatrix} \, , \,\, H=\begin{bmatrix} -5 \\ -2 \end{bmatrix}$ نسبت به مبدا مختصات برابر است با

$D^{'}=\begin{bmatrix} -6 \\ -7 \end{bmatrix} \,\,\, ,\,\,\, E^{'}=\begin{bmatrix} -6 \\ +2 \end{bmatrix}$

$F^{'}=\begin{bmatrix} +5 \\ -7 \end{bmatrix} \,\,\, ,\,\,\, H^{'}=\begin{bmatrix} +5 \\ +2 \end{bmatrix}$

قرینه نقاط $A=\begin{bmatrix} +6 \\ 0 \end{bmatrix} \, ,\,\, B=\begin{bmatrix} 0 \\ +4 \end{bmatrix} \, ,\,\, C=\begin{bmatrix} 0 \\ -2 \end{bmatrix} \, , \,\, G=\begin{bmatrix} -3 \\ 0 \end{bmatrix}$ نسبت به مبدا مختصات برابر است با

$A^{'}=\begin{bmatrix} -6 \\ 0 \end{bmatrix} \,\,\, ,\,\,\, B^{'}=\begin{bmatrix} 0 \\ -4 \end{bmatrix}$

$C^{'}=\begin{bmatrix} 0 \\ +2 \end{bmatrix} \,\,\, ,\,\,\, G^{'}=\begin{bmatrix} +3 \\ 0 \end{bmatrix}$

جمع بندی

در این مقاله به آموزش صفحه مختصات پرداختیم بعد از خواندن این مقاله می توانید مختصات هر نقطه ای در صفحه مختصات را پیدا کنید. و برای هر مختصاتی یک نقطه در صفحه مختصات پیدا کنید همچنین می توانید قرینه یک نقطه را نسبت به مبدا مختصات محور طول و محور عرض پیدا کنید. لطفا نظرات خود را در مورد مقاله مختصات در قسمت کامنت ها بیان کنید.

آموزش جامع صفحه مختصات و نقاط روی آن

دستگاه مختصات و چهار ناحیه آن

مختصات یک نقطه در صفحه مختصات چگونه بدست می آید؟

چطور قرینه یک نقطه را نسبت به محورهای مختصات و مبدا آن بدست آوریم؟

دیدگاهتان را بنویسید لغو پاسخ

آخرین مطالب وبلاگ

دنباله های عددی

تابع خطی و معادله خط

تابع و دامنه و برد آن

تعیین علامت

عبارت و معادله گویا

معادله درجه دوم

معادله

عبارت جبری

قدرمطلق

دوره ها

دسترسی سریع

دسترسی سریع

مقالات مادر