آموزش کامل مقاطع مخروطی و انواع آن

مقاطع مخروطی حاصل برخورد یک صفحه با رویه مخروطی است. دایره، بیضی، خط، سهمی و هذلولی مقاطع مخروطی هستند. همه ی این اشکال حاصل برخورد صفحه با زوایای مختلفی با یک رویه مخروطی است. در این مقاله به بررسی نحوه بوجود آمدن مقاطع مخروطی می پردازیم. همچنین به آموزش نکاتی درمورد بیضی می پردازیم. از آنجا که نکات مربوط به دایره، سهمی و خط بسیار مفصل می باشد هر کدام را در مقاله ای جداگانه بررسی کرده ایم. اگر علاقمند به یادگیری مقاطع مخروطی و همه ی انواع آن هستید این مقاله را از دست ندهید.

رویه مخروطی چیست؟

برای اینکه به آموزش مقاطع مخروطی بپردازیم ابتدا باید بدانیم که رویه مخروطی چیست. در ادامه به تعرویف رویه مخروطی می پردازیم:

رویه مخروطی: فرض کنید دو خط $d$ و $l$ در نقطه $A$ مانند شکل متقاطع (غیرعمود) باشند. سطح حاصل از دوران $d$ حول $l$ را یک رویه مخروطی (سطح مخروطی) می نامیم. در این حالت خط $l$ را محور، نقطه $A$ را راس وخط $d$ را مولد این سطح مخروطی می نامیم .

از برخورد یک صفحه با رویه مخروطی چه شکل هایی بوجود می آید؟

حالا که فهمیدیم رویه مخروطی چیست می توانیم فصل مشترک یک صفحه با رویه مخروطی را در حالات مختلف بررسی کنیم. در ادامه فصل مشترک صفحه و رویه مخروطی و مقاطع مخروطی حاصل را بررسی می کنیم.

اگر صفحه بر محور سطح مخروطی عمود باشد و از راس آن عبور نکند شکل حاصل یک دایره است.

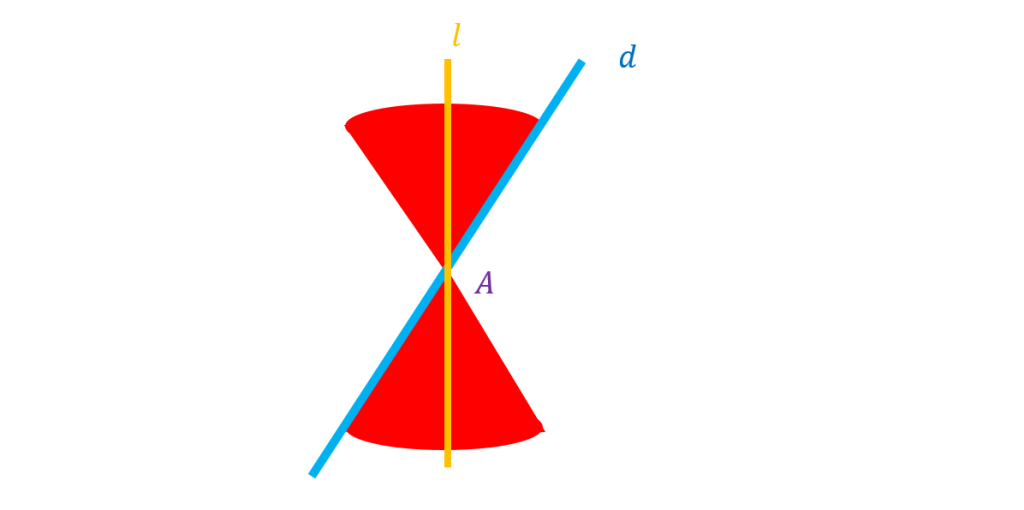
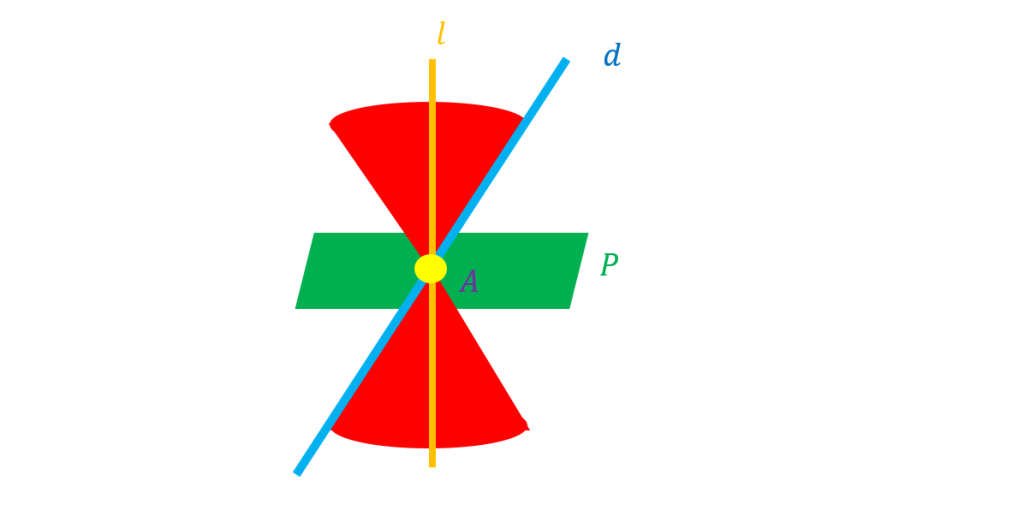
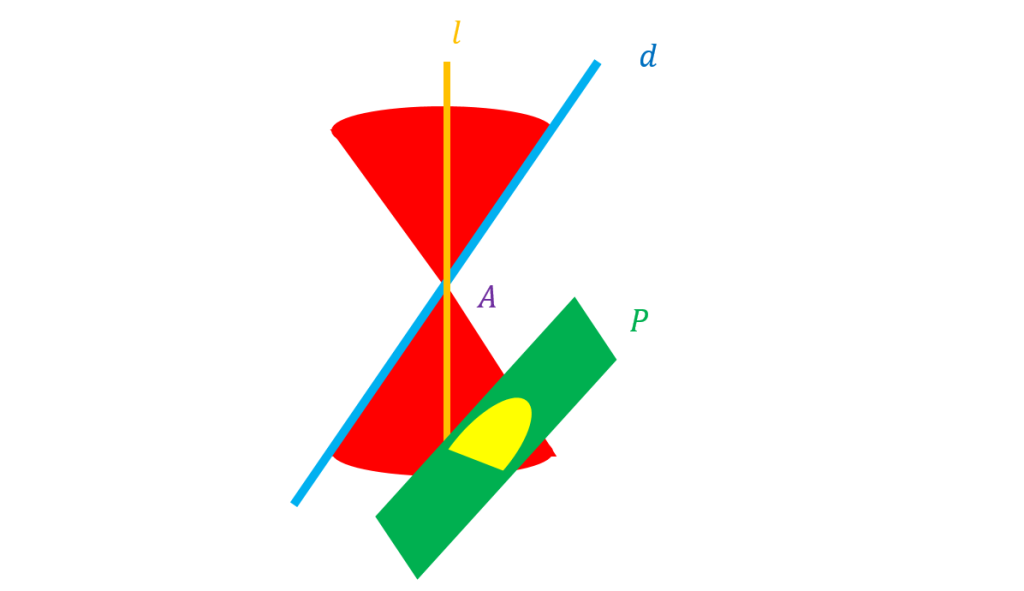
اگر صفحه بر محور سطح مخروطی عمود باشد و از راس آن عبور کند شکل حاصل یک نقطه است.

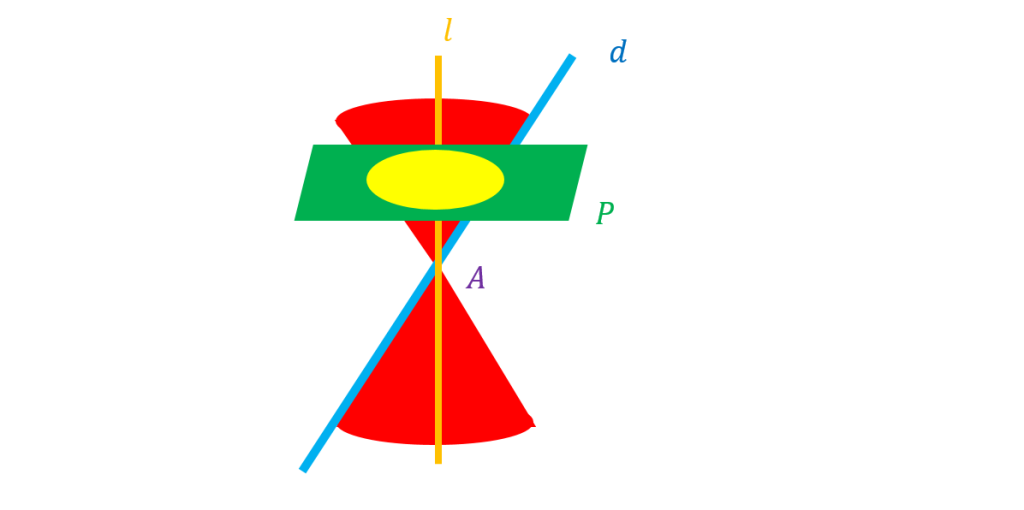
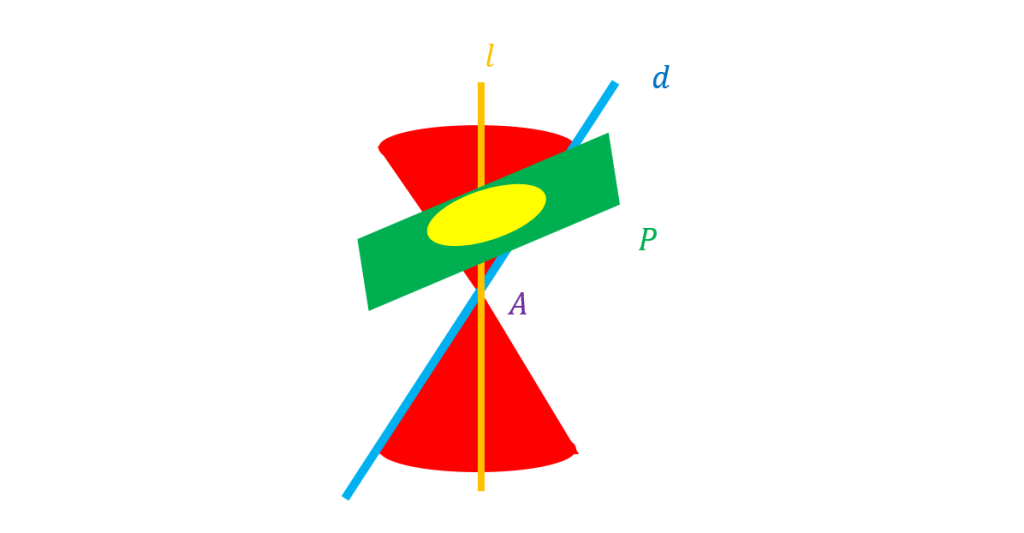
اگر صفحه بر محور سطح مخروطی عمود نباشد و با مولد موازی نباشد و فقط یکی از دو نیمه مخروط را قطع کند سطح حاصل یک بیضی خواهد بود.

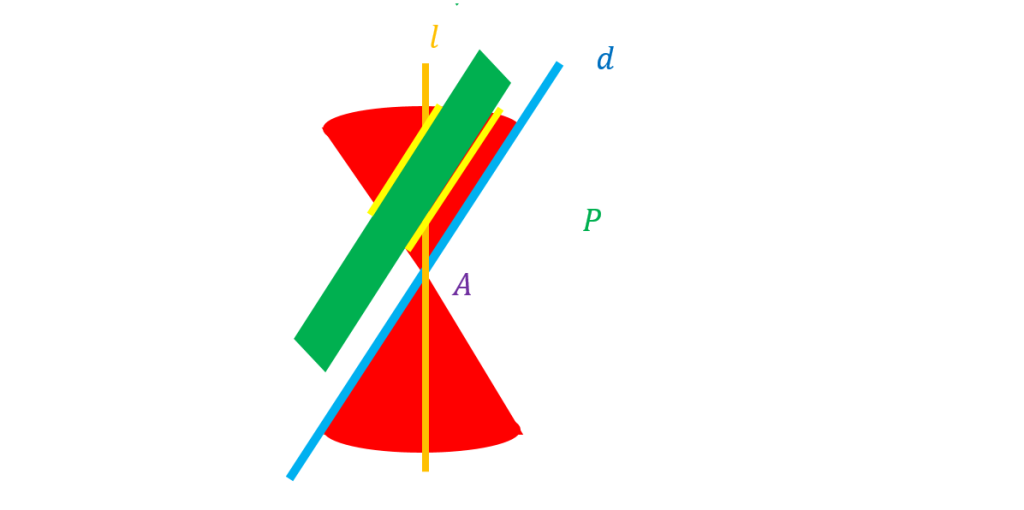
اگر صفحه با مولد موازی باشد و از راس عبور نکند سطح حاصل یک سهمی است.

اگر صفحه با مولد موازی باشد و از راس عبور کند سطح حاصل یک خط است.

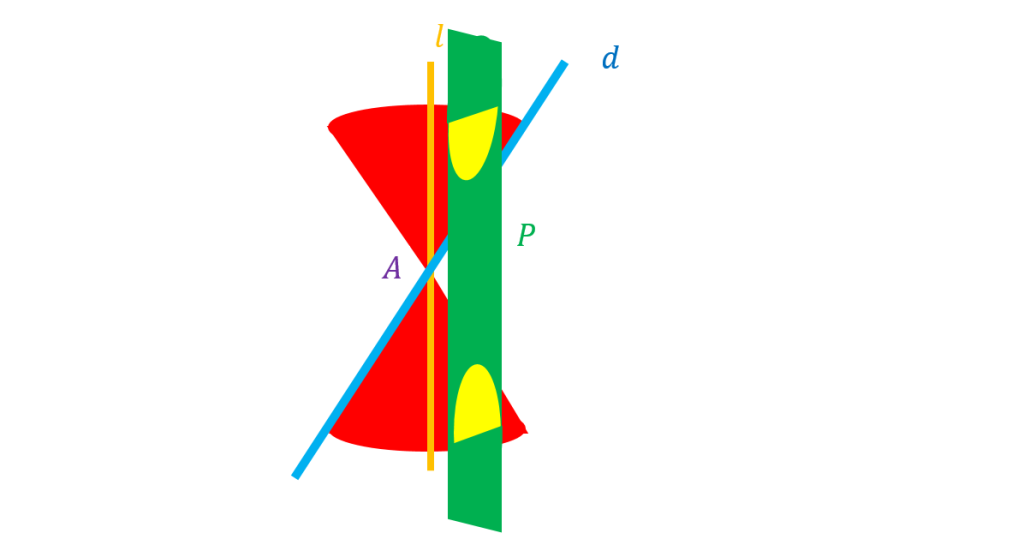
اگر صفحه طوری باشد که هر دو تکه بالایی و پایینی سطح مخروطی را قطع کند و شامل محور نباشد سطح بدست آمده یک هذلولی است .

بیضی مکان هندسی نقاطی از صفحه است که مجموع فاصله شان از دو نقطه $F$ و $F^{'}$ ثابت است. به نقطه $F$ و $F^{'}$ کانون های بیضی می گویند.

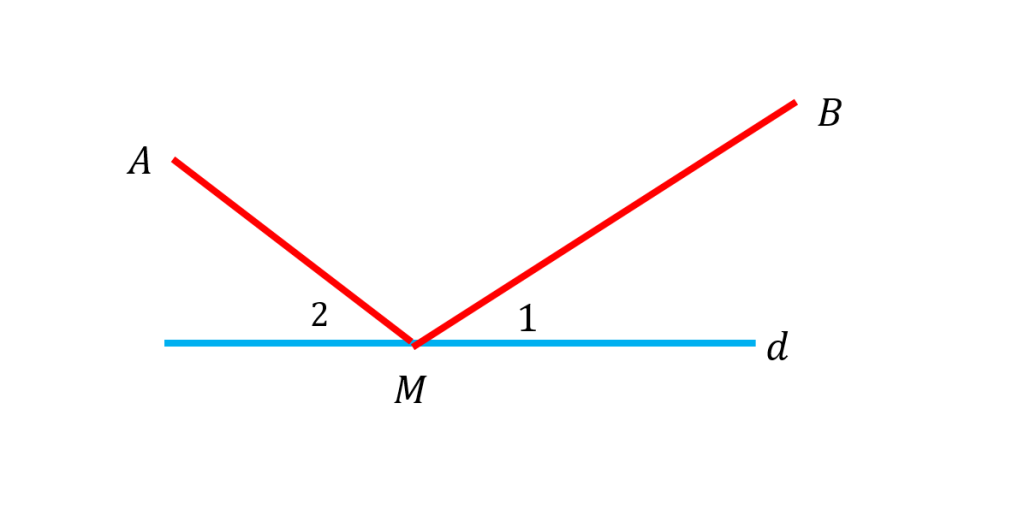
نکته: کوتاهترین مسیر از نقطه $A$ به نقطه $B$ و با عبور از نقطه ای دلخواه از خط $d$ از نقطه ای مانند $M$ روی خط $d$ می گذرد به گونه ای که دو زاویه ایجاد شده $M_{1}$ و $M_{2}$ با هم برابرند.

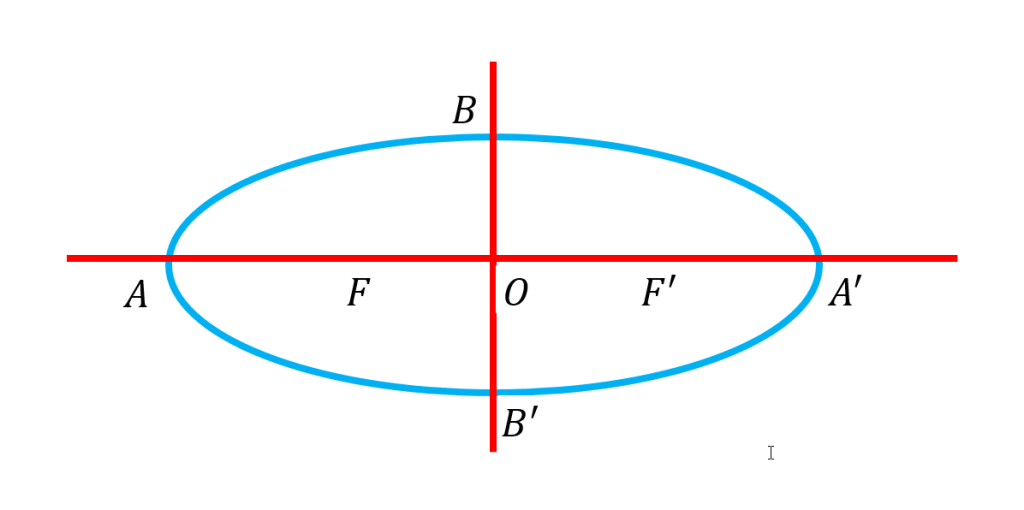
شکل زیر یک بیضی را نشان می دهد $AA^{'}$ قطر بزرگ (قطر کانونی) و $BB^{'}$ قطر کوچک بیضی هستند. $FF^{'}$ فاصله کانونی بیضی است.

در این شکل $F$ و $F^{'}$ کانون های بیضی و $O$ وسط پاره خط های $ff^{'}$ و $AA^{'}$ و $BB^{'}$ مرکز بیضی است.

اگر $OA=a\,\,\,,\,\,\,OB=b\,\,\,,\,\,\,OC=c$ در نظر بگیریم. فاصله کانونی برابر $FF^{'}=2c$ اندازه قطر بزرگ برابر $AA^{'}=2a$ و اندازه قطر کوچک برابر $BB^{'}=2b$ می باشد.

توجه: بین $A\,\,\,,\,\,\,b\,\,\,,\,\,\,c$ رابطه ی زیر برقرار است:

$b^{2}+c^{2}=a^{2}$

از آنجا که همواره $0 \le \frac{c}{a} \le 1$ اگر $e=\frac{c}{a}$ را خروج از مرکز بیضی معرفی کنیم، می توان گفت هر چه $e$ به $1$ نزدیک تر باشد شکل بیضی کشیده تر و بیشتر شبیه به خط می شود. و هر چه $e$ به $0$ نزدیکتر باشد شکل بیضی به دایره شبیه تر می شود.

جمع بندی

در مقاله حاضر توضیحاتی راجع به مقاطع مخروطی و نحوه بوجود آمدن هر کدام از مقاطع مخروطی کردیم. همچنین ذکر کردیم خط، سهمی و دایره که از مقاطع مخروطی هستند را در مقاله های جداگانه بررسی کردیم چرا که نکات زیادی در مورد هر کدام قابل بحث می باشد. در این مقاله فقط به بررسی بیضی پرداختیم. اگر علاقمند به یادگیری هر کدام از مباحث دایره، سهمی و خط هستید لطفا به مقالات مربوطه مراجعه کنید. اما اگر علاقمند به نکات کاملی از بیضی هستید این مقاله را از دست ندهید و مارا از نظرات ارزشمندتان در مورد مقاله مقاطع مخروطی در قسمت کامنت ها بهره مند کنید.

آموزش کامل مقاطع مخروطی و انواع آن

رویه مخروطی چیست؟

از برخورد یک صفحه با رویه مخروطی چه شکل هایی بوجود می آید؟

دیدگاهتان را بنویسید لغو پاسخ

آخرین مطالب وبلاگ

دنباله های عددی

تابع خطی و معادله خط

تابع و دامنه و برد آن

تعیین علامت

عبارت و معادله گویا

معادله درجه دوم

معادله

عبارت جبری

قدرمطلق

دوره ها

دسترسی سریع

دسترسی سریع

مقالات مادر