جامع ترین آموزش در مورد تبدیل های هندسی(تقارن، انتقال، دوران)
تبدیل های هندسی به تبدیل هایی می گویند که یک شکل را تبدیل به یک شکل دیگر می کند. تقارن، دوران، انتقال، بازتاب و تجانس از جمله تبدیل های هندسی هستند که در این مقاله مورد بررسی قرار گرفتند. در هر مورد شکل هایی برای فهم بیشتر رسم شده اند و تاثیر هر تبدیل بر شیب خط، طول پاره خط، اندازه زاویه، مساحت شکل و جهت شکل بررسی شده است.
تفکر تجسمی چیست؟
در تفکر تجسمی از عبارات و جملات و شیوه های زبانی برای تفکر استفاده نمی شود؛ بلکه این تصاویر هستند که در ذهن ما نقش می بندند و به ما کمک می کنند دربارۀ موضوع مورد نظر فکر کنیم.
مثلا اینکه نمای بالا یا پایین یا چپ یا راست یک حجم را بخواهیم رسم کنیم نیاز به تفکر تجسمی داریم یعنی باید در ذهن خود تجسم کنیم که آن نما چگونه است.
تبدیل های هندسی هر شکل را چگونه تبدیل می کنند؟
تبدیلهای هندسی مطرح شده در این مقاله می تواند موقعیت و جایگاه شکل در صفحه یا اندازۀ شکل را تغییر دهد. تبدیل یافتۀ یک شکل را، تصویر آن می نامیم.
انتقال، تقارن، بازتاب، دوران و تجانس را تبدیل های هندسی می نامیم.
به طور شهودی می توان دید که بازتاب، انتقال و دوران، می توانند موقعیت شکل را تغییر دهند ولی اندازه پاره خط ها و زاویه ها را تغییر نمی دهند.
تبدیل: تبدیل 
در صفحه 
تابعی است که به هر نقطه 
از صفحه دقیقا یک نقطه مانند 
را از همان صفحه نظیر می کند و برعکس؛ هر نقطه ی از صفحه تصویر دقیقا یک نقطه از همان صفحه است. اگر تبدیل را با حرف نمایش دهیم به اختصار می نویسیم:
![\[T\,\,:\,\,P\,\,\rightarrow\,\,P\,\,\,\,,\,\,\,\,T(A)=A^{'}\]](https://faramath.com/core/ql-cache/quicklatex.com-2e97afba694e329366ca785a8e191f1a_l3.png "Rendered by QuickLaTeX.com")
تبدیل طولپا: تبدیل هایی که طول پاره خط را حفظ می کنند تبدیلات طولپا (ایزومتری) نامیده می شوند. به عبارتی اگر داشته باشیم : 
و 
آنگاه داریم 
هر تبدیل طولپا اندازه زاویه را حفظ می کند. مثلا بازتاب تقارن انتقال و دوران تبدیل های طولپا هستند.
قضیه: در هر تبدیل طولپا تبدیل یافته ی هر زاویه، زاویه ای هم اندازه با آن است.
تعریف: در هر تبدیل، نقطه ای را که تبدیل یافتۀ آن بر خود آن نقطه منطبق می شود، نقطۀ ثابت تبدیل می نامند.
بنابراین بازتاب نسبت به خط، بیشمار نقطه ثابت تبدیل دارد.
در ادامه به توضیح هر کدام از تبدیل ها می پردازیم.
تبدیل تقارن چه نوع تبدیلی است؟
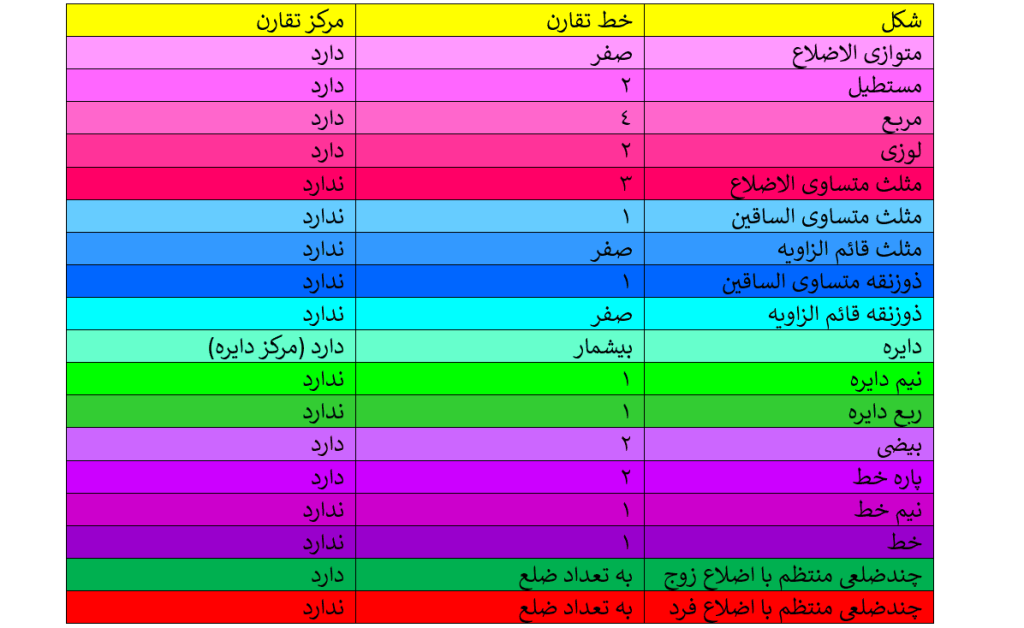
خطی که یک شکل را دو قسمت می کند و دو طرف این خط قرینه ی یکدیگرند را خط تقارن می گویند. به شکل هایی که خط تقارن دارند می گویند شکل، تقارن محوری دارد.
تعریف: تبدیل طولپای را تبدیل تقارنی شکل 
می نامیم به شرط اینکه تبدیل یافتۀ شکل ، تحت آن تبدیل بر خود شکل منطبق شود؛ یعنی داشته باشیم:
![\[T(F)=F\]](https://faramath.com/core/ql-cache/quicklatex.com-0ed485cdaebe7939e00d6cd7366a9a0a_l3.png "Rendered by QuickLaTeX.com")
به طور کلی اگر شکلی به اندازه ی 180 بچرخد تصویری که ایجاد می شود قرینه شکل اصلی است.
اگر شکلی را حول یک نقطه، 180 درجه دوران دهیم و نتیجه دوران، روی خودش منطبق شود، می گوییم شکل مرکز تقارن دارد و نقطه مورد نظر، مرکز تقارن شکل است.
وقتی قرینه شکلی را نسبت به یک خط پیدا می کنیم، تصویر به دست آمده مساوی با آن شکل است اما جهت آن تغییر می کند.
در جدول زیر اشکال و تعداد خط تقارن و نقطه تقارن آنها در صورت وجود بیان شده است:
دوران چگونه تبدیلی است؟
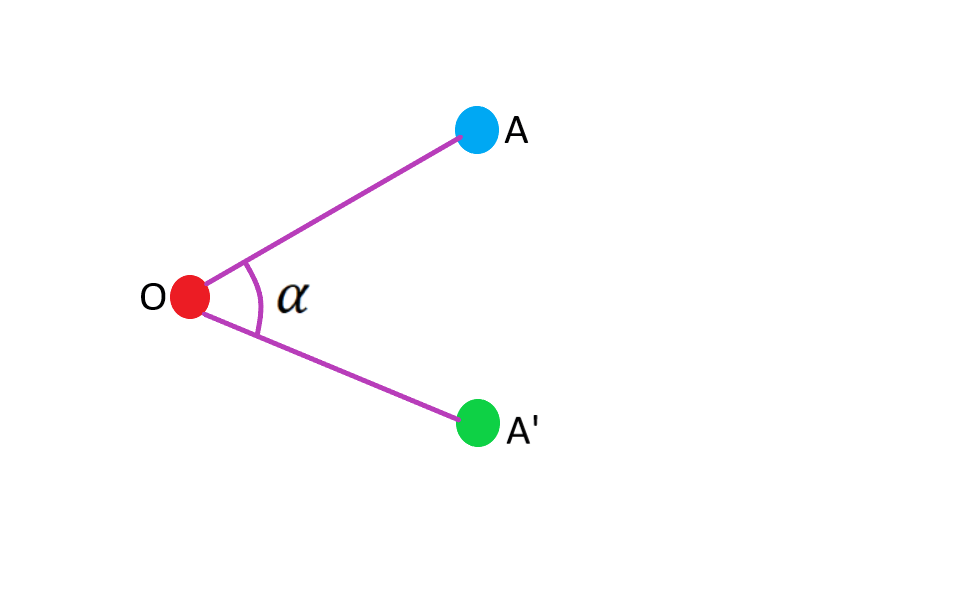
چرخیدن حول یک نقطه را دوران می گویند و آن نقطه را مرکز دوران می گویند.
تعریف : دوران 
به مرکز نقطه ثابت 
و زاویه 
تبدیلی از صفحه است که در آن اگر تصویر نقطه باشد داریم :
![\[OA=OA^{'} \,\,\,,\,\,\, \widehat{AOA^{'}}=\alpha\]](https://faramath.com/core/ql-cache/quicklatex.com-7a6f1856be15a921e31ceb09054dbab6_l3.png "Rendered by QuickLaTeX.com")
قضیه : در هر دوران اندازه هر پاره خط و تصویر آن با هم برابرند.
وقتی شکلی را حول یک نقطه به اندازه 180 درجه یا کمتر در جهت عقربه های ساعت می چرخانیم و شکل روی خودش می افتد می گوییم شکل، تقارن چرخشی دارد.
تعریف: تقارن دورانی با زاویه 
را تقارن مرکزی نیز می نامند. در این حالت مرکز دوران را مرکز تقارن شکل می گویند.
دوران حول یک محور
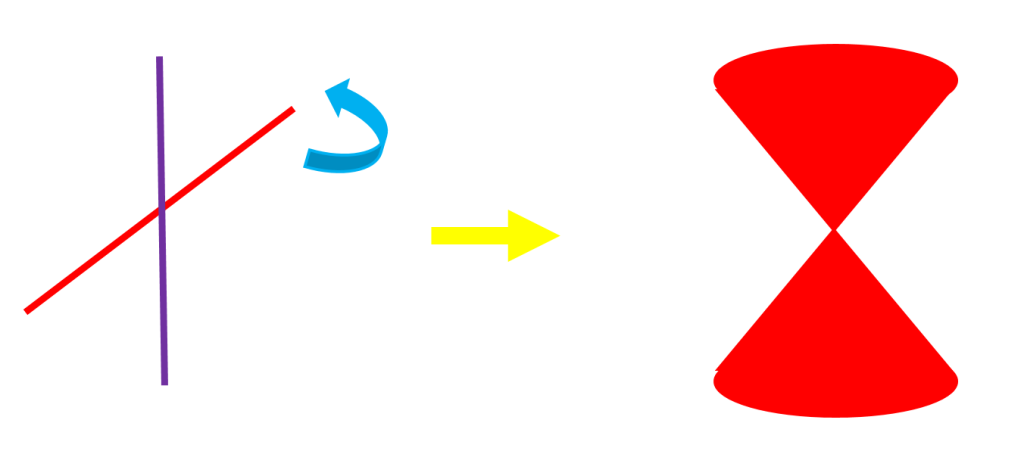
اگر به جای اینکه دوران را حول یک نقطه انجام دهیم، حول یک خط انجام دهیم می گوییم دوران محوری انجام داده ایم.
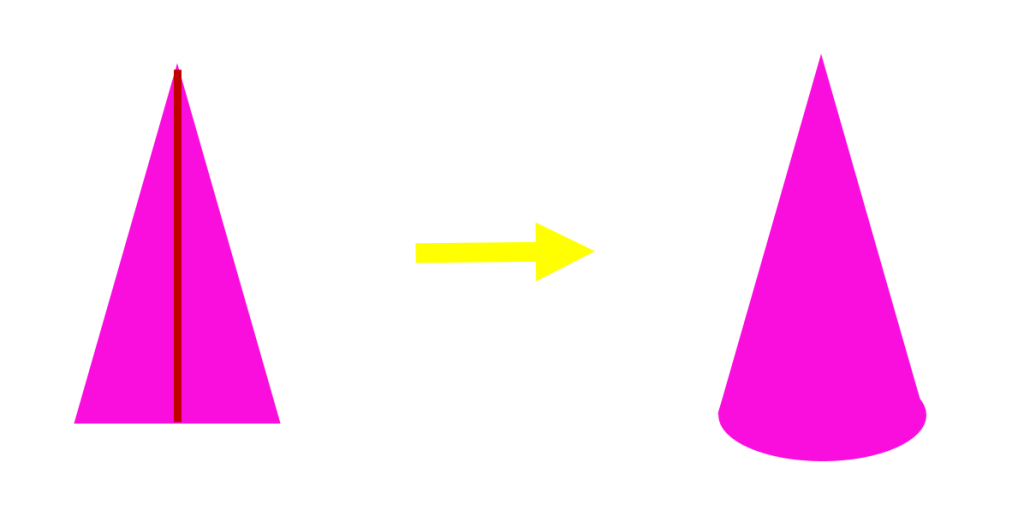
دوران یک مثلث متساوی الساقین حول ارتفاع وارد بر قاعده تشکیل یک مخروط می دهد.
دوران یک مثلث قائم الزاویه حول یک ضلع زاویه قائمه تشکیل مخروط می دهد.
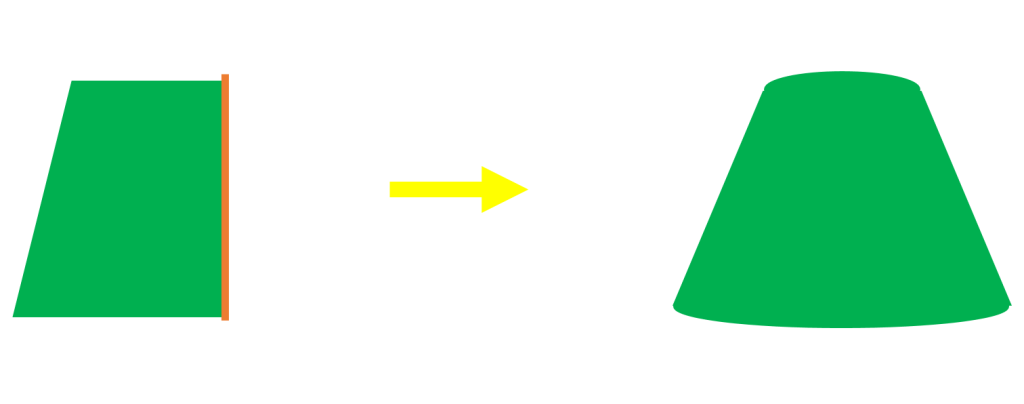
دوران یک ذوزنقه قائم الزاویه حول ضلع عمود بر قاعده ها تشکیل مخروط ناقص می دهد.
بازتاب چه نوع تبدیلی است؟
برای پیدا کردن بازتاب یک نقطه مثل نسبت به خط 
کافی است از نقطه به خط داده شده عمودی وارد کنیم و پای عمود را 
بنامیم حال 
را از سمت به اندازه خودش امتداد می دهیم تا بدست آید. در این صورت را بازتاب یا قرینه نسبت به خط می نامیم و می نویسیم 
در چنین حالتی خط عمودمنصف پاره خط 
خواهد بود. خط خط بازتاب یا محور بازتاب نامیده می شود.
اگر نقطه ای روی خط بازتاب باشد تصویر آن بر خودش منطبق می شود.
تعریف : در هر تبدیل نقطه ای را که تبدیل یافته آن بر خود آن نقطه منطبق می شود نقطه ثابت تبدیل می نامند. بنابراین بازتاب نسبت به خط بیشمار نقطه ثابت تبدیل دارد.
قضیه : در هر بازتاب اندازه هر پاره خط و اندازه تصویر آن با هم برابرند.
در حالت کلی بازتاب شیب خط را حفظ نمی کند.
طولپاها اندازه زاویه را هم حفظ می کنند. بنابراین به طور کلی هر چندضلعی و تصویر آن تحت تأثیر یک طولپا از جمله بازتاب با هم همنهشت هستند.
تعریف: اگر شکلی تحت یک بازتاب بر خودش منطبق شود، گوییم آن شکل تقارن بازتابی خطی دارد و اگر آن شکل تحت دورانی با زاویۀ 
بر خودش منطبق شود، گوییم تقارن دورانی چرخشی دارد.
انتقال چه نوع تبدیلی است؟
اگر شکلی را بدون تغییر جهت روی صفحه حرکت دهیم یعنی عمل انتقال را انجام دادیم.
وقتی شکلی را روی صفحه انتقال می دهیم، تصویر بدست آمده مساوی و هم جهت شکل اولیه است.
تعریف : انتقال T تحت بردار v تبدیلی از صفحه است که در آن تصویر هر نقطه از صفحه نقطه ای مانند در همان صفحه است که 
قضیه : در هر انتقال اندازه هر پاره خط و اندازه تصویر آن با هم برابرند.
تجانس چه نوع تبدیلی است؟
تعریف : اگر نقطه ای ثابت در صفحه و 
یک عدد حقیقی باشد نقطه 
را مجانس نقطه 
در تجانس به مرکز و نسبت تجانس (مقیاس تجانس) 
گوییم هرگاه سه شرط زیر برقرار باشد:
شرط 1: سه نقطه و و روی یک خط راست باشند.
شرط 2: 
شرط 3 : اگر مثبت باشد روی نیم خط 
و نقاط و در یک طرف قرار دارند. در این حالت تجانس را مستقیم گوییم.
توجه: اگر منفی باشد نقطه بین و قرار می گیرد. در این حالت تجانس را معکوس گوییم.
نکته : در تجانس مساحت شکل جدید 
برابر شکل اول است.
نکته : در تجانس شیب خط و جهت شکل و اندازه زاویه حفظ می شود.
نکته تجانس فقط به ازای 
و 
طولپاست و مساحت را حفظ می کند.
نکته : در تجانس خطوطی که هر نقطه را به تصویرش وصل می کنند در مرکز تجانس همرسند.
نکته در تجانس اگر 
تصویر شکل کوچک می شود و آن را انقباض می نامیم.
نکته: در تجانس اگر 
تصویر شکل بزرگ می شود و آن را انبساط می نامیم.
نکته : دو شکل متشابه الزاما متجانس نیستند. دو شکل متجانس الزاما متشابه هستند.
تبدیل همانی چه نوع تبدیلی است؟
تعریف : تبدیل را تبدیل همانی گوییم هرگاه به ازای هر نقطه از صفحه داشته باشیم:
![\[T(A)=A\]](https://faramath.com/core/ql-cache/quicklatex.com-f8ac19707c95801ecb63db011a9824c3_l3.png "Rendered by QuickLaTeX.com")
معمولا تبدیل های همانی را با 
نشان می دهند پس 
- بازتاب نقاط ثابت دارد اما هیچ گاه همانی نیست.
- انتقال زمانی تبدیل همانی است که بردار انتقال برابر با بردار صفر باشد.
- دوران زمانی تبدیل همانی است که زاویه دوران 360 درجه باشد
- تجانس زمانی تبدیل همانی است که در آن
باشد.
باشد.- تبدیل همانی طولپا است.
- در انتقال غیر همانی نقطه ثابت نداریم
- در دوران غیر همانی مرکز دوران همان نقطه ثابت است.
- در تجانس غیر همانی مرکز تجانس همان نقطه ثابت است.
نکاتی در مورد تبدیل های هندسی
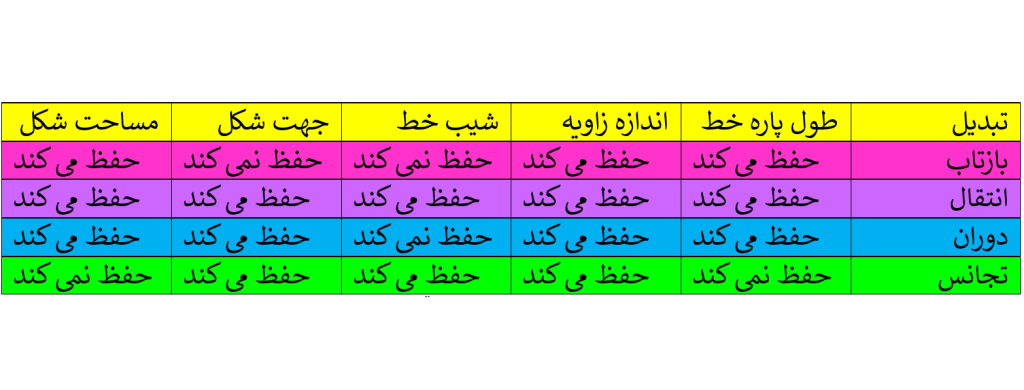
بازتاب طول پاره خط و اندازه زاویه و مساحت شکل را حفظ می کند اما شیب خط و جهت شکل را حفظ نمی کند.
انتقال طول پاره خط و اندازه زاویه و شیب خط و جهت شکل و مساحت شکل را حفظ می کند.
دوران طول پاره خط و اندازه زاویه و جهت شکل و مساحت شکل را حفظ میکند ولی شیب خط را حفظ نمی کند.
تجانس اندازه زاویه و شیب خط و جهت شکل را حفظ می کند اما طول پاره خط و مساحت شکل را حفظ نمی کند.
در همه ی تبدیل های بررسی شده در این مقاله، تبدیل هر خط یک خط است پس می توان تبدیل دو نقطه از خط را پیدا کرد و آن دو نقطه را به هم وصل کنیم تا خط تبدیل یافته را پیدا کنیم .
جمع بندی
در این مقاله به بررسی انواع تبدیل های هندسی پرداختیم. تقارن، دوران، بازتاب، انتقال، تجانس و تبدیل همانی از جمله تبدیل هایی بودند که در این مقاله بررسی شدند همچنین در این مقاله بررسی کردیم هر کدام از این موارد چه تاثیری بر شیب خط، طول پاره خط، اندازه زاویه، جهت شکل و مساحت شکل دارند. لطفا نظرات خود را در مورد مقاله تبدیل های هندسی در قسمت کامنت ها بیان کنید.
