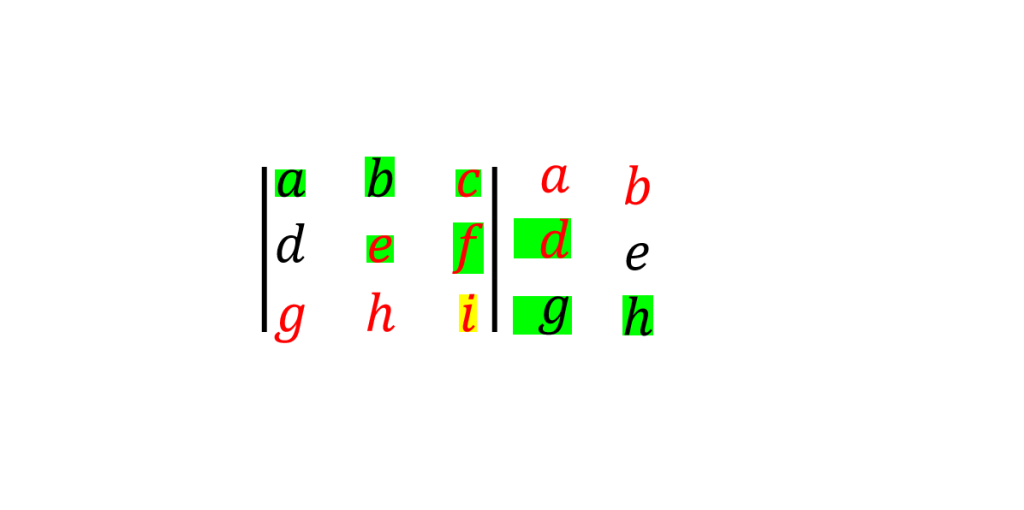همه چیز درباره ماتریس ها

ماتریس ها یک آرایش مستطیلی از اعداد حقیقی هستند که در این مقاله به معرفی آنها پرداختیم. ماتریس های خاصی مانند ماتریس مربعی سطری ستونی قطری اسکالر و صفر را معرفی کردیم. اعمال جبری بین ماتریس ها مانند جمع بین دو ماتریس تفریق بین دو ماتریس ضرب عدد در ماتریس ضرب بین دو ماتریس قرینه یک ماتریس را بیان کردیم. شرایط لازم برای مساوی بودن دو ماتریس و ضرب دو ماتریس در هم را بیان کردیم. نحوه بدست آوردن دترمینان یک ماتریس دو در دو و یک در یک را آموزش دادیم و در نهایت نحوه بدست آوردن وارون یک ماتریس و حل دستگاه معادلات با کمک آن را بیان کردیم. اگر می خواهید همه نکات در مورد ماتریس را برای کنکور یکجا یاد بگیرید این آموزش را از دست ندهید.

ماتریس چیست و چگونه نمایش داده می شود؟

تعریف: هر آرایش مستطیلی از اعداد حقیقی شامل تعدادی سطر و ستون یک ماتریس نامیده می شود. هر عدد حقیقی واقع در هر ماتریس را درایه ی آن ماتریس می نامیم.

معمولا ماتریس ها را با نام بزرگ مانند $A,B,C,…$ نام گذاری می کنیم.

در حالت کلی اگر ماتریسی مانند $A$ دارای $m$ سطر و $n$ ستون باشد می نویسیم $A_{m \times n}$ و می خوانیم ” $A$ ماتریسی از مرتبه $m$ در $n$ است. ” برای هر درایه ی ماتریس برای مشخص کردن جایگاه آن دو اندیس در نظر می گیریم که اندیس چپ جای سطر و سمت راست جای ستون آن درایه را مسخص می کند. $a_{ij}$ یعنی درایه روی سطر $i$ ام و ستون $j$ ام قرار دارد.

درایه $a_{ij}$ که $1 \le i \le m \,\,\,,\,\,\, 1 \le j \le n$ درایه عمومی نام دارد. همه ی درایه های ماتریس $A$ را می توان توسط درایه عمومی نشان داد و برای اختصار می نویسیم

$A=[a_{ij}]_{m \times n}$

ماتریس ها چه انواعی دارند؟

در ادامه ماتریس های مربعی، سطری، ستونی، اسکالر و صفر معرفی می شوند.

ماتریس مربعی

اگر در ماتریس $A$ تعداد سطرها با تعداد ستون ها برابر و مساوی $n$ باشد $A$ را ماتریس مربعی از مرتبه $n$ می نامیم.

در ماتریس $A=\begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix}$ درایه های $a_{11},a_{22},a_{33}$ را قطر اصلی می نامیم. به طور کلی اگر $i=j$ در این صورت درایه $a_{ij}$ روی قطر اصلی قرار دارد.

ماتریس سطری

اگر ماتریس فقط دارای یک سطر باشد به آن ماتریس سطری می نامیم.

ماتریس ستونی

اگر ماتریس فقط دارای یک ستون باشد آن را ماتریس ستونی می نامیم.

ماتریس قطری

ماتریسی است که تمام درایه های غیر واقع بر قطر اصلی آن صفر باشند. درایه های قطر اصلی می تواند صفر باشد یا نه.

ماتریس اسکالر

ماتریس قطری که تمام درایه های قطر اصلی آن با هم برابر باشند آن را ماتریس اسکالر می نامیم.

ماتریس صفر

ماتریسی که همه ی درایه های آن صفر باشد ماتریس صفر می نامیم و با $\overline{O}$ نشان می دهیم.

اعمال جبری در ماتریس ها چگونه انجام می شود؟

در ادامه شرایط تساوی دو ماتریس و شربیط و نحوه جمع و تفریق دو ماتریس، ضرب عدد در ماتریس، قرینه یک ماتریس و در نهایت ضرب ماتریس ها را بیان می کنیم.

تساوی بین دو ماتریس

دو ماتریس هم مرتبه، مساوی اند اگر تمام درایه های نظیر با هم برابر باشند.

جمع و تفریق دو ماتریس

برای جمع یا تفریق دو ماتریس هم مرتبه $A$ و $B$ کافی است درایه های نظیر به نظیر با هم جمع یا از هم کم کنیم که حاصل ماتریسی از همان مرتبه $A$ و $B$ است.

$A=[a_{ij}]_{m \times n} \,\,,\,\,B=[b_{ij}]_{m \times n}$

$A \pm B =[a_{ij}]\pm [b_{ij}]=[a_{ij}\pm b_{ij}]$

ضرب عدد حقیقی در یک ماتریس

تعریف: برای ضرب یک عدد حقیقی در ماتریسی چون $A$ آن عدد را در تمام درایه های ماتریس ضرب می کنیم، به عبارت دیگر می توان نوشت:

$A=[a_{ij}]_{m \times n} \,\,,\,\, r \in \Bbb{R}$

$\rightarrow rA=r[a_{ij}]_{m \times n}=[ra_{ij}]_{m \times n}$

قرینه یک ماتریس

اگر $A=[a_{ij}]_{m \times n}$ ماتریسی دلخواه باشد قرینه ماتریس $A$ را با $-A$ نمایش داده و از ضرب $(-1)$ در ماتریس $A$ به دست می آید. واضح است که

$A+(-A)=\overline{O}$

ویژگی های جمع و ضرب ماتریس ها

خواص مهم جمع ماتریس ها و ضرب عدد در ماتریس را در ادامه می بینید:

اگر $A , B, C$ ماتریس هایی $m \times n$ (هم مرتبه) و $r,s$ اعدادی حقیقی باشند داریم:

$A+B=B+A$
$A+(B+C)=(A+B)+C$
$A+\overline{O}=\overline{O}+A$
$A+(-A)=\overline{O}$
$(-A)+A=\overline{O}$
$r(A \pm B)=rA \pm rB$
$(r \pm s)A=rA\pm sA$
$rA=rB \,\, \text{and} \,\, r\neq 0 \Rightarrow A=B$
$A=B \,\,\Rightarrow \,\, rA=rB$

ضرب ماتریس سطری در ماتریس ستونی

اگر ماتریس $A$ سطری و ماتریس $B$ ستونی باشد و تعداد ستون های ماتریس $A$ با تعداد سطر های $B$ برابر باشد. حاصل ضرب $A \times B$ برابر یک ماتریس $1 \times 1$ یا یک عدد حقیقی می شود.

ضرب دو ماتریس در حالت کلی

اگر $A$ ماتریسی $m \times p$ و $B$ ماتریسی $p \times n$ باشد (تعداد ستون های ماتریس $A$ با تعداد سطرهای $B$ برابر باشد) در این صورت $A_{mp} \times B_{pn}$ قابل تعریف بوده و اگر فرض کنیم $A_{mp} \times B_{pn}=C_{mn}=[c_{ij}]$ ، ماتریس $C$ ماتریسی $m \times n$ بوده که درایه ی روی سطر $i$ ام $A$ در ستون $j$ ام $B$ در آن یعنی $c_{ij}$ از ضرب سطر $i$ ام $A$ در ستون $j$ ام $B$ بدست می آید.

ویژگی ضرب ماتریس ها

در این بخش خواص ضرب ماتریس هایی که امکان ضرب شدن را دارند می بینیم.

نکته: در حالت کلی ضرب ماتریس ها خاصیت جابجایی ندارد.

ماتریس اسکالر $I_{n}=\begin{bmatrix} 1&0&…&0 \\ 0 & 1 &…&0 \\ …& …&…&… \\ 0&0&…&1\end{bmatrix}$ که آن را ماتریس واحد یا همانی مرتبه $n$ می نامیم عضو خنثی برای عمل ضرب ماتریس های مربعی مرتبه $n$ است یعنی:

$A_{n\times n}\times I_{n}=I_{n} \times A_{n \times n}=A_{n \times n}$

اگر بتوان ماتریس ها را در هم ضرب کرد خواص زیر برقرار است:

$A\times (B+C)=(A \times B)+(A \times C)$

$A\times (B \times C)=(A \times B) \times C$

در ضرب ماتریس ها برخلاف ضرب اعداد اگر حاصلضرب دو ماتریس صفر شود الزاما یکی از آنها صفر نیست می توانند هر دو ماتریس صفر نباشند اما حاصل ضرب شان صفر باشد. یعنی اگر $A\times B=\overline{O}$ الزاما $A=\overline{O}$ یا $B=\overline{O}$ برقرار نیست.

دترمینان یک ماتریس چگونه بدست می آید؟

اگر $A$ ماتریس مربعی از مرتبه $n$ باشد $(1 \le n \le 3)$ در اینصورت دترمینان ماتریس $A$ را با نماد $det(A)=|A|$ نمایش می دهیم و داریم :

$|A|=[k]_{1 \times 1 } \,\rightarrow \,|A|=k$

$A=\begin{bmatrix} a & b \\ c & d \end{bmatrix}\,\rightarrow \,|A|=ad-bc$

$A=\begin{bmatrix} a_{11} & a_{12}& a_{13} \\ a_{21}& a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix}$

$\rightarrow\,\,\,|A|=a_{11}\times (-1)^{1+1} \times \begin{vmatrix} a_{22} & a_{23} \\ a_{32} & a_{33} \end{vmatrix}$

$+ a_{12}\times (-1)^{1+2} \times \begin{vmatrix} a_{21} & a_{23} \\ a_{31} & a_{33} \end{vmatrix}$

$+ a_{13}\times (-1)^{1+3} \times \begin{vmatrix} a_{21} & a_{22} \\ a_{31} & a_{32} \end{vmatrix}$

برای هر ماتریس $3 \times 3$ دلخواه می توان دترمینان $A$ را بر حسب هر سطر یا ستونی بدست آورد که در همه حالت ها مقدار دترمینان یکسان است.

دستور ساروس برای محاسبه دترمینان ماتریس سه در سه

دستور ساروس برای محاسبه دترمینان ماتریس های $3 \times 3$ در این روش دو ستون اول و دوم ماتریس را کنار آن می نویسیم. یعنی به شکل زیر عمل می کنیم:

دترمینان $A$ برابر است با مجموع حاصل ضرب های درایه های واقع بر قطر اصلی و دو قطر موازی آن (درایه های سبز رنگ) منهای مجموع حاصلضرب های درایه های واقع بر قطر فرعی $A$ و دو قطر موازی آن (درایه های قرمز رنگ )

$|A|=(aei+bfg+cdh)-(ceg+afh+bdi)$

نکته : دترمینان هر ماتریس قطری برابر است با حاصل ضرب اعداد روی قطر اصلی.

نکته: دترمینان ماتریس مربعی صفر، صفر است.

دترمینان ماتریس چه کاربردی در هندسه دارد؟

دترمینان در هندسه برای مساحت مثلث و متوازی الاضلاع ِ(در مورد متوازی الاضلاع می توانید در مقاله چندضلعی ها بخوانید) پدید آمده توسط دو بردار به کار می رود. با کمک محسابه دترمینان ماتریس های سه در سه می توان حجم متوازی السطوح حاصل از سه بردار را به دست آورد و نیز در محاسبه ضرب خارجی دو بردار استفاده کرد.

وارون یا معکوس یک ماتریس چگونه بدست می آید؟

برای هر ماتریس مربعی مانند $A$ وارون ماتریس $A$ در صورت وجود ماتریسی است چون $B$ به طوری که $A \times B =B \times A=I$ . در این صورت $B$ را وارون $A$ می نامیم و با $A^{-1}$ نشان می دهیم.

اگر $A=\begin{bmatrix}a & b \\ c & d \end{bmatrix}$ در این صورت وارون ماتریس $A$ یعنی $A^{-1}$ از تساوی زیر بدست می آید:

$A^{-1}=\frac{1}{|A|}\begin{bmatrix} d & -b \\ -c & a \end{bmatrix}$

نکته: اگر $|A|=0$ ماتریس $A$ وارون پذیر نیست و وارون ش وجود ندارد.

نکته: اگر وارون یک ماتریس مربعی وجود داشته باشد حتما منحصربفرد است.

چگونه دستگاه معادلات را با استفاده از ماتریس وارون حل کنیم؟

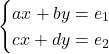
در حالت کلی اگر $A=\begin{bmatrix}a& b \\ c &d\end{bmatrix}$ ماتریس ضرایب و $B=\begin{bmatrix} e_{1} \\ e_{2} \end{bmatrix}$ ماتریس مقادیر معلوم و $X=\begin{bmatrix} x \\ y \end{bmatrix}$ ماتریس مجهولات دستگاه دو معادله و دو مجهول ِ $\begin{cases} ax+by=e_{1} \\ cx+dy=e_{2}\end{cases}$ باشند در این صورت دستگاه مذکور به شکل معادله ماتریسی $AX+B$ نوشته شده و در صورتی که ماتریس $A$ وارون پذیر باشد یا $|A| \neq 0$ با ضرب $A^{-1}$ از چپ در معادله فوق می توان مجهول ها را بصورت زیر بدست آورد:

$AX=B$

$\rightarrow \,A^{-1}(AX)=A^{-1}B$

$\rightarrow \,\,\,(A^{-1}A)X=A^{-1}B$

$\rightarrow\,\,\, IX=A^{-1}B$

$\rightarrow \,\,\,X=A^{-1}B$

نکته: هدف از حل یک دستگاه دو معادله و دو مجهول، پیدا کردن $x$ و $y$ ای است که در هر دو معادلۀ دستگاه که هرکدام معادلۀ یک خط هستند، صدق کند و تعبیر هندسی حل دستگاه دو معادله و دو مجهول پیدا کردن مختصات محل برخورد دو خط است.

در دستگاه معادله 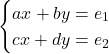$\begin{cases}ax+by=e_{1} \\ cx+dy=e_{2}\end{cases}$ داریم:

اگر $\frac{a}{c} \neq \frac{b}{d}$ در اینصورت دو خط متقاطع اند و دستگاه یک جواب یکتا دارد.

اگر $\frac{a}{c}=\frac{b}{d}\neq \frac{e_{1}}{e_{2}}$ در اینصورت دو خط موازی اند و هیچ نقطه مشترکی ندارند و دستگاه هیچ جوابی ندارد.

اگر $\frac{a}{c}=\frac{b}{d}= \frac{e_{1}}{e_{2}}$ در اینصورت دو خط بر هم منطبق اند و دستگاه بیشمار جواب دارد.

اگر ماتریس $A=\begin{bmatrix} a & b \\ c & d \end{bmatrix}$ ماتریس ضرایب یک دستگاه معادله باشد می توان گفت اگر $|A| \neq 0$ آنگاه دستگاه دارای یک جواب منحصربفرد است. و اگر $|A|=0$ در اینصورت دستگاه یا جواب ندارد (دو خط موازی اند) یا بیشمار جواب دارد.(دو خط منطبق اند)

جمع بندی

در این مقاله به آموزش ماتریس پرداختیم. انواع ماتریس را نام بردیم و به بررسی اعمال جبری مانند جمع و تفریق و ضرب بین ماتریس ها پرداختیم. شرایط تساوی بین ماتریس ها و شرایط ضرب بین ماتریس ها را بیان کردیم و خواص جمع و تفریق و ضرب ماتریس ها را بیان کردیم. در نهایت گفتیم که چه راه هایی برای بدست آوردن دترمینان ماتریس های دو در دو و سه در سه وجود دارد. در آخر مقاله را بیان نحوه بدست آوردن وارون یک ماتریس و حل دستگاه معادلات به کمک آن به پایان رساندیم. امیدواریم از خواندن این مقاله لذت و استفاده لازم را برده باشید. لطفا نظرات خود را در مورد مقاله ماتریس بیان کنید.

همه چیز درباره ماتریس ها

ماتریس چیست و چگونه نمایش داده می شود؟

ماتریس ها چه انواعی دارند؟

اعمال جبری در ماتریس ها چگونه انجام می شود؟

دترمینان یک ماتریس چگونه بدست می آید؟

وارون یا معکوس یک ماتریس چگونه بدست می آید؟

چگونه دستگاه معادلات را با استفاده از ماتریس وارون حل کنیم؟

دیدگاهتان را بنویسید لغو پاسخ

آخرین مطالب وبلاگ

دنباله های عددی

تابع خطی و معادله خط

تابع و دامنه و برد آن

تعیین علامت

عبارت و معادله گویا

معادله درجه دوم

معادله

عبارت جبری

قدرمطلق

دوره ها

دسترسی سریع

دسترسی سریع

مقالات مادر