همه چیز درمورد چندضلعی ها (تعریف و انواع چندضلعی ها)
چندضلعی ها به هر خط شکسته بسته گفته می شوند به شرط آنگه ضلع ها همدیگر را قطع نکنند مگر در راس ها. در این مقاله به بیان تعریف چندضلعی و انواع آن یعنی چندضلعی محدب، چندضلعی مقعر و چندضلعی منتظم می پردازیم. مثلث، مربع، مستطیل، لوزی، متوازی الاضلاع و ذوزنقه از چندضلعی هایی هستند که در این مقاله آنها را معرفی کردیم. اگر خواهان دانستن محیط و مساحت هر کدام از اشکال هندسی هستید یا می خواهید از تعداد خطوط تقارن یا داشتن مرکز تقارن هر کدام از اشکال با خبر شوید به ترتیب به مقالات محیط و مساحت و تبدیل های هندسی مراجعه کنید. برای خواندن این مقاله نیاز به دانستن تعاریف پاره خط ، زاویه ، نیمساز و عمومنصف دارید در صورت لزوم لطفا به مقاله هندسه تحلیلی مراجعه نمایید.
به چه شکلی چندضلعی می گویند؟
به هر خط شکسته بسته چندضلعی گفته می شود به شرط آنکه ضلع ها همدیگر را قطع نکنند؛ مگر در راس ها که دو ضلع به هم می رسند.
تعریف: 
ضلعی شکلی است شامل 
پاره خط متوالی که:
1)هر پاره خط دقیقا دو پاره خط دیگر را در نقاط انتهایی خودش قطع کند.
2)هر دو پاره خط که در یک انتها مشترک اند، روی یک خط نباشند.
*در هر ضلعی، هر پاره خط را که دو انتهای آن، دو راس غیر مجاور باشند قطر می نامند.
* هر دو ضلع چندضلعی را که در یک انتها مشترک اند، دو ضلع مجاور و نقطه مشترک آن دو را راس می نامند.
هر دو زاویه چندضلعی که هر دو در یک ضلع ِ چندضلعی مشترک اند دو زاویه مجاور به آن ضلع در چندضلعی می نامند.
نکته: در هر ضلعی تعداد قطرها برابر 
است.
چند ضلعی ها بر چند نوع اند؟
چندضلعی ها به دو دسته محدب و مقعر تقسیم می شوند.
تعریف: یک ضلعی را محدب می گوییم هرگاه با در نظر گرفتن خط شامل هر ضلع آن، بقیه نقاط چندضلعی در یک طرف آن خط واقع شوند. یا یک چندضلعی محدب است؛ اگر هر پاره خطی که دو نقطه ی دلخواهِ درون آن چندضلعی را به هم وصل می کند، به طور کامل درون آن چندضلعی قرار بگیرد. هر چندضلعی که محدب نباشد، مقعر است.
به طور کلی به چند ضلعی هایی که هیچ زاویه بزرگتر از 180 درجه ندارند، محدب (کوژ) می گوییم و به چند ضلعی هایی که دست کم یک زاویه بزرگتر از 180 درجه داشته باشند، چندضلعی مقعر(کاو) می گوییم.
چندضلعی منتظم: به چندضلعی هایی که همه ی اضلاع و زاویه هایشان با هم مساوی است، چندضلعی منتظم گفته می شود.
زوایای داخلی و خارجی چندضلعی ها چند درجه اند؟
زاویه هایی که درون یک چندضلعی قرار دارند، زاویه های داخلی آن چند ضلعی نامیده می شوند.
- مجموع زوایای داخلی یک سه ضلعی ( مثلث) 180 درجه است.
- مجموع زوایای داخلی یک چهارضلعی 360 درجه است.
- هر
ضلعی را با رسم قطرهایش از یکی از راس ها می توان به 
مثلث تقسیم کرد.
مثلث تقسیم کرد.نکته: مجموع زوایای یک ضلعی برابر است با : 
نکته: اندازه هر زاویه داخلی یک ضلعی منتظم برابر است با 
- مجموع زوایای خارجی همه ی چند ضلعی ها 360 درجه است.
- اندازه هر زاویه خارجی یک ضلعی منتظم برابر است با
.
.نکته: زاویه ای که در هر راس یک چندضلعی محدب، بین یک ضلع و امتداد ضلع دیگر تشکیل می شود، زاویه خارجی آن راس نامیده می شود.
- در هر مثلث اندازه زاویه خارجی برابر با مجموع دو زاویه داخلی غیرمجاور آن است.
- اگر اندازه سه زاویه از یک چهارضلعی نامشخص را بدانیم زاویه چهارم هم بدست می آید.
- اگر اندازه یک زاویه از یک لوزی را بدانیم اندازه سه زاویه دیگر هم بدست می آید. (زاویه روبروی آن زاویه برابر با زاویه مورد نظر و دو زاویه دیگر مکمل آن زاویه است.)
- اگر اندازه یک زاویه از متوازی الاضلاع را بدانیم اندازه سه زاویه دیگر هم بدست می آید. (زاویه روبروی آن زاویه برابر با زاویه مورد نظر و دو زاویه دیگر مکمل آن زاویه است.)
مثلث
به هر سه ضلعی مثلث می گویند. هر مثلث سه زاویه دارد که مجموع زوایای آن برابر با 180 درجه است.
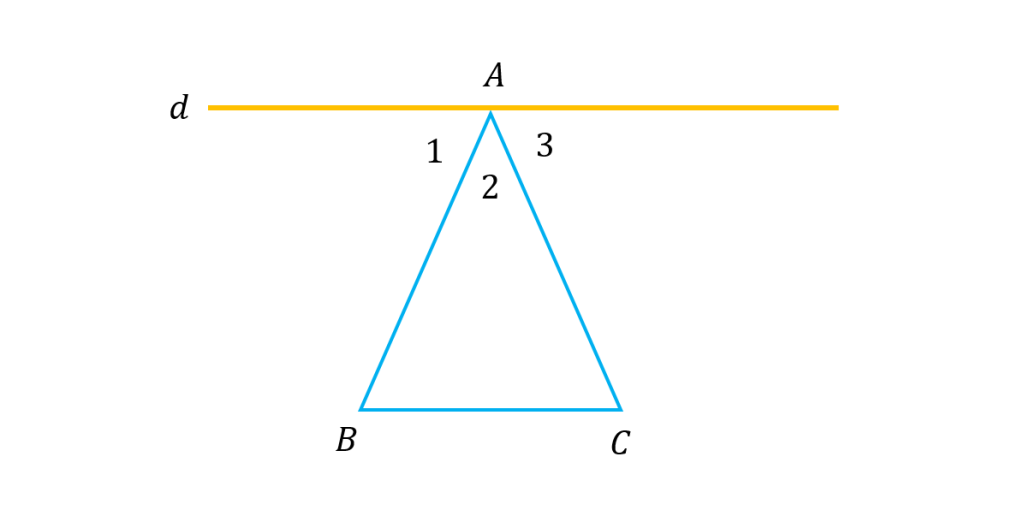
همانطور که در شکل زیر می بینیم اثبات می شود مجموع زوایای داخلی مثلث برابر 180 است.
![\[d\parallel BC\,\, \rightarrow\,\, A_{1}=B\,\,\,,\,\,\,A_{3}=C\]](https://faramath.com/core/ql-cache/quicklatex.com-a822f90ddc3d9b068970df8a539c8ece_l3.png "Rendered by QuickLaTeX.com")
![\[A_{1}+A_{2}+A_{3}=180\]](https://faramath.com/core/ql-cache/quicklatex.com-a45b9d67d1db5f15fc6ba6770f954af9_l3.png "Rendered by QuickLaTeX.com")
![\[\Rightarrow\,B+A_{2}+C=180\]](https://faramath.com/core/ql-cache/quicklatex.com-474dd98dbc233b841577d5506962b89f_l3.png "Rendered by QuickLaTeX.com")
اگر می خواهید همه چیز را در مورد مثلث بدانید به مقاله مربوطه مراجعه کنید.
مربع
تعریف: مربع چهارضلعی ای است که، هر چهار ضلع آن هم اندازه و حداقل یک زاویه آن قائمه باشد.
نکته: در مربع همه زاویه ها با هم برابرند و همه ی ضلع ها با هم برابرند.
نکته: قطرهای مربع با هم برابر و عمودمنصف یکدیگرند.
مستطیل
تعریف: مستطیل چهارضلعی ای است که همه ی زاویه های آن قائمه باشند.
- در مستطیل همه ی زاویه ها با هم برابر و قائمه اند ضلع های رو به رو با هم برابر و موازی اند.
- قطر ها در مستطیل با هم برابرندو همدیگر را نصف می کنند.
- هر چهارضلعی که قطرهایش با هم برابر و منصف هم باشد مستطیل است.
لوزی
تعریف : لوزی چهارضلعی ای است که هر چهار ضلع آن هم اندازه باشند.
- در لوزی زاویه های روبرو با هم برابرند و همه ی ضلع های آن برابرند.
- در هر لوزی قطرها عمودمنصف یکدیگرند. و قطرها همان نیمساز زوایا هستند.
- هر چهارضلعی که قطرهایش عمودمنصف یکدیگر باشند لوزی است.
کایت یا شبه لوزی: کایت چهارضلعی، شامل فقط دوجفت متمایز، از ضلع های مجاور با اندازه های برابر است. در واقع کایت چهارضلعی محدبی است که دارای دو قطر عمود بر هم است و فقط یکی از قطرهای منصف قطر دیگر می باشد. قطری که منصف قطر دیگر است محور تقارن کایت و همچنین نیمساز دو زاویه مقابل است. مساحت کایت مانند مساحت لوزی محاسبه می شود. در واقع کایت اجتماع دو مثلث متساوی الساقین است که قاعده های آنها مشترک و دو رأس دیگر دو مثلث در دو طرف خطی باشند که قاعده مشترک روی آن واقع است. سپس قاعده مشترک را حذف کرده باشیم
متوازی الاضلاع
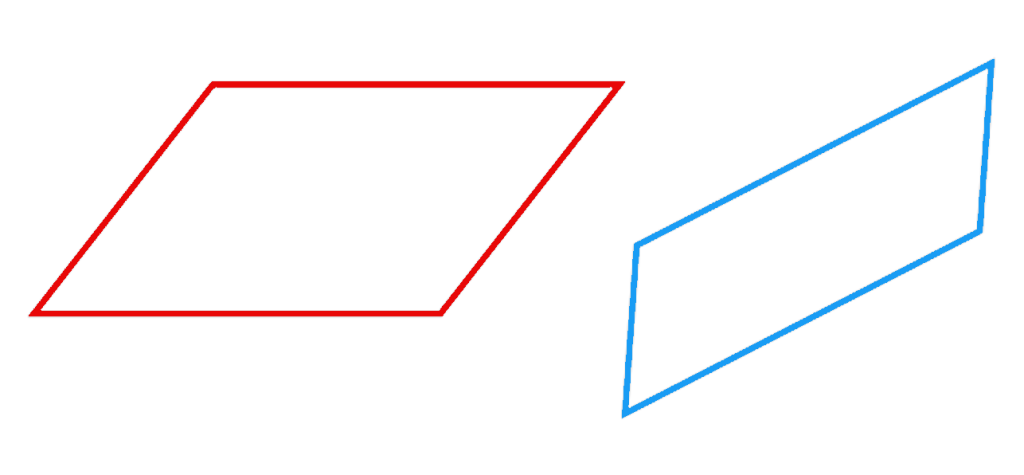
تعریف : متوازی الاضلاع چهارضلعی ای است که ضلع های روبرویش دو به دو موازی باشند.
قضیه 1: در هر متوازی الاضلاع هر دو ضلع مقابل هم اندازه اند.
عکس قضیه 1: اگر در یک چهارضلعی ، ضلع های مقابل دو به دو هم اندازه باشند، چهارضلعی متوازی الاضلاع است.
قضیه 2: در متوازی الاضلاع هر دو زاویه مجاور مکمل اند.
عکس قضیه 2: هر چهارضلعی که هر دو زاویه مجاور آن مکمل باشند، متوازی الاضلاع است.
قضیه 3: در هر متوازی الاضلاع هر دو زاویه مقابل هم اندازه اند.
عکس قضیه 3: اگر در یک چهارضلعی هر دو زاویه مقابل هم اندازه باشند چهارضلعی متوازی الاضلاع است
قضیه 4: در هر متوازی الاضلاع قطرها همدیگر را نصف می کنند.
عکس قضیه 4: هر چهار ضلعی که قطرهایش منصف یکدیگرند متوازی الاضلاع است.
- اگر در یک چهارضلعی دو ضلع موازی و مساوی باشند چهارضلعی متوازی الاضلاع است.
- در هر متوازی الاضلاع زاویه های روبرو با هم برابرند و زاویه های مجاور مکمل اند.
- در هر متوازی الاضلاع ضلع های رو برو دو به دو با هم برابرند.
- در هر متوازی الاضلاع قطرها همدیگر را نصف می کنند.
- هر چهارضلعی که قطرهایش منصف هم باشند متوازی الاضلاع است. و برعکس
- هر چهارضلعی که دو ضلع مقابل آن هم اندازه و موازی باشند متوازی الاضلاع است.
ذوزنقه
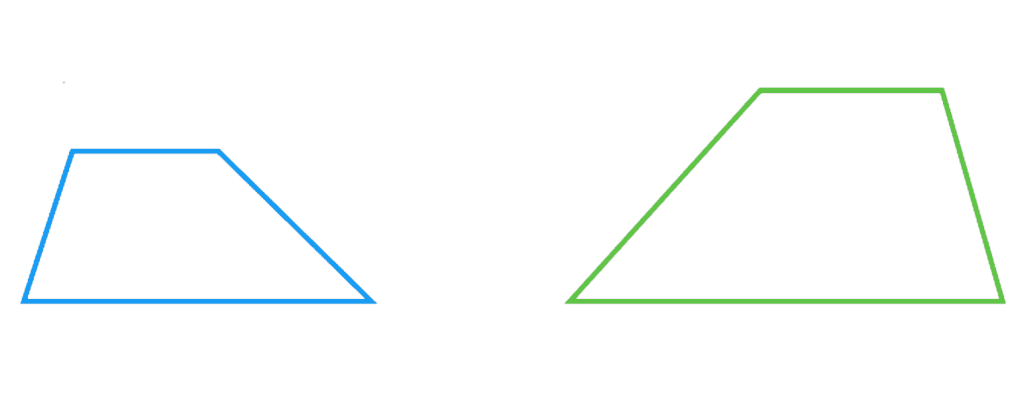
به چهارضلعی ای که فقط دو ضلع موازی دارد ذوزنقه می گویند.
- به دو ضلع موازی ذوزنقه قاعده می گویند و به دو ضلع غیرموازی ساق می گویند.
- اگر در یک ذوزنقه دو ساق با هم برابر باشند آن ذورنقه یک ذوزنقه متساوی الساقین است.
- در هر مستطیل قطرها با هم برابرند. اما اگر یک چهارضلعی قطرهایش برابر باشند الزاما مستطیل نیست می تواند ذوزنقه متساوی الساقین باشد.
- اگر در یک ذوزنقه یک ساق بر یک قاعده عمود باشد مسلما بر قاعده دیگر هم عمود است و به آن ذوزنقه قائم الزاویه می گویند.
- در هر ذوزنقه متساوی الساقین زاویه های مجاور به یک قاعده هم اندازه اند.
- اگر در یک ذوزنقه دو زاویه مجاور به یک قاعده هم اندازه باشند، ذوزنقه متساوی الساقین است.
- در هر ذوزنقه متساوی الساقین قطرها اندازه های مساوی دارند و برعکس اگر در یک ذوزنقه قطرها مساوی بودند ذوزنقه متساوی الساقین است.
بین چهارضلعی ها چه رابطه ای وجود دارد؟
مستطیل متوازی الاضلاعی است که زاویه های قائمه دارد.
لوزی متوازی الاضلاعی است که چهار ضلع برابر دارد.
مربع متوازی الاضلاعی است که چهار ضلع مساوی و زاویه های قائمه دارد.
همه خواص متوازی الاضلاع برای لوزی مستطیل و مربع برقرار است.
اگر وسط های اضلاع یک چندضلعی را به هم وصل کنیم چه شکلی ایجاد می شود؟
اگر وسط های اضلاع هر چهارضلعی را به هم وصل کنیم متوازی الاضلاع بدست می آید و مساحت شکل حاصل نصف مساحت شکل اصلی است.
- اگر وسط های اضلاع یک متوازی الاضلاع را به هم وصل کنیم متوازی الاضلاع بدست می آید و مساحت شکل حاصل نصف مساحت شکل اصلی است.
- اگر وسط های اضلاع یک مستطیل را به هم وصل کنیم لوزی بدست می آید و مساحت شکل حاصل نصف مساحت شکل اصلی است.
- اگر وسط های اضلاع یک لوزی را به هم وصل کنیم مستطیل بدست می آید و مساحت شکل حاصل نصف مساحت شکل اصلی است.
- اگر وسط های اضلاع یک مستطیل را به هم وصل کنیم لوزی بدست می آید و مساحت شکل حاصل نصف مساحت شکل اصلی است.
- اگر وسط های اضلاع یک مربع را به هم وصل کنیم مربع بدست می آید و مساحت شکل حاصل نصف مساحت شکل اصلی است.
- نکته: از تقاطع نیمسازهای داخلی یک متوازی الاضلاع، مستطیل بدست می آید.
نکته: از تقاطع نیمسازهای داخلی یک مستطیل، مربع بدست می آید.
- اگر وسط های یک چهارضلعی با قطرهای عمود برهم را بهم وصل کنیم مستطیل پدید می آید.
- اگر وسط های یک چهارضلعی با قطرهای برابر را بهم وصل کنیم لوزی پدید می آید.
جمع بندی
در این مقاله به آموزش تعریف چندضلعی و بیان انواع آن پرداختیم. چندضلعی محدب، مقعر و منتظم بیان شد. زاویه داخلی و خارجی چندضلعی ها تعریف شد و روابط مربوط به زوایای چندضلعی ها را بیان کردیم. هر کدام از اشکال هندسی مثلث، مربع، مستطیل، لوزی، متوازی الاضلاع و ذوزنقه را معرفی کردیم و برخی از خواص و ویژگی های هر کدام و روابط شان با یکدیگر را آموزش دادیم. اما اگر می خواهید راجع به نحوه محاسبه محیط و مساحت هر کدام بدانید به مقاله محیط و مساحت مراجعه کنید. و اگر می خواهید بدانید هر کدام مرکز تقارن دارند یا نه و هر کدام چند خط تقارن دارند به مقاله تبدیل های هندسی مراجعه کنید. لطفا نظرات خود را در مورد مقاله چندضلعی ها در قسمت کامنت ها بیان کنید.
