همه چیز درباره ی تشابه اشکال هندسی، مثلث و قضیه تالس را دراین مقاله بخوانید

تشابه دو شکل هندسی به معنای این است که نسبت اضلاع دو شکل برابر با مقدار ثابتی است که این مقدار ثابت نسبت تشابه نام دارد. در این مقاله به بررسی نسبت و تناسب و خواص آن پرداختیم. سپس بیان کردیم که دو چندضلعی در چه صورت با هم متشابه اند. در این مقاله به طور اختصاصی تشابه دو مثلث بررسی شده است. قضیه اساسی تشابه مثلث ها نیز بیان شده و در ادامه به بیان قضیه تالس پرداخته شده است. تعمیم قضیه تالس، عکس قضیه تالس و قضیه تالس در ذوزنقه نیز در این مقاله آموزش داده شده است. در نهایت مقاله را با بیان کاربردهایی از قضیه تالس و تشابه مثلث ها به پایان رساندیم.

ویژگی اصلی دو کسر دارای نسبت و تناسب چیست؟

اگر دو کسر با هم برابر باشند می گوییم دو کسر نسبت و تناسب دارند. ویژگی اصلیِ دو کسر با نسبت و تناسب، برابری ضرب طرفین و وسطین است:

$\frac{a}{b}=\frac{c}{d} \,\,\,(b,d \neq 0)\,\,\, \leftrightarrow \,\,\, ad=bc$

توجه کنید اعداد صورت و مخرج هر عدد حقیقی ای می توانند باشند و فقط مخرج ها نمی توانند صفر باشند.

نکته: منظور از طرفین صورت یک کسر و مخرج کسر دیگر است. آن دو عدد دیگر یعنی صورت کسر دوم و مخرج کسر اول همان وسطین هستند.

توجه: تفاوتی نمی کند که کدام جفت را طرفین و کدام جفت را وسطین بگیریم.

ویژگی های دو کسر دارای نسبت و تناسب در ریاضی چیست؟

تناسب دو کسر در علم ریاضی خواص زیر را دارد. یعنی اگر داشته باشیم $\frac{a}{b}=\frac{c}{d}$ که $(b,d \neq 0)$ آنگاه نتایج زیر برقرارند:

$\ ad=bc$
$(a,c,b,d \neq 0)\,\, \leftrightarrow \,\, \frac{b}{a}=\frac{d}{c}$
$(a,c,b,d \neq 0)\,\,\, \leftrightarrow \,\,\, \frac{d}{b}=\frac{c}{a}$
$(a,c,b,d \neq 0)\,\,\, \leftrightarrow \,\,\, \frac{a}{c}=\frac{b}{d}$
$\frac{a+b}{b}=\frac{c+d}{d}$
$\frac{a}{a+b}=\frac{c}{c+d}$
$\frac{a-b}{b}=\frac{c-d}{d}$
$\frac{a}{a-b}=\frac{c}{c-d}$
$\frac{a+b}{b+d}=\frac{a}{b}=\frac{c}{d}$

تعریف واسطه (میانگین) هندسی: اگر طرفین یا وسطین یک تناسب شامل دو عدد برابر باشد یعنی $\frac{a}{b}=\frac{b}{c}$ با طرفین وسطین کردن نتیجه می شود: $b^{2}=ac$ . در این صورت $b$ را واسطه هندسی $a$ و $c$ می نامیم.

چه موقع می گوییم دو شکل هندسی متشابه اند؟

هرگاه در دو چندضلعی همه ی ضلع ها به یک نسبت تغییر کرده باشد (کوچک یا بزرگ شده باشد یا بدون تغییر باشد) و اندازه زاویه ها تغییر نکرده باشد، آن دو چندضلعی با هم متشابه اند.

به نسبت دو ضلع متناظر در دو شکل متشابه، نسبت تشابه می گویند.

هر دو شکل هم نهشت متشابه اند و نسبت تشابه آنها یک است.

هر دو $n$ ضلعی منتظم با هم متشابه اند.

هر دو مربع دلخواه با هم متشابه اند.

هر دو مثلث متساوی الاضلاع دلخواه با هم متشابه اند.

شرایط تشابه دو مثلث چیست؟

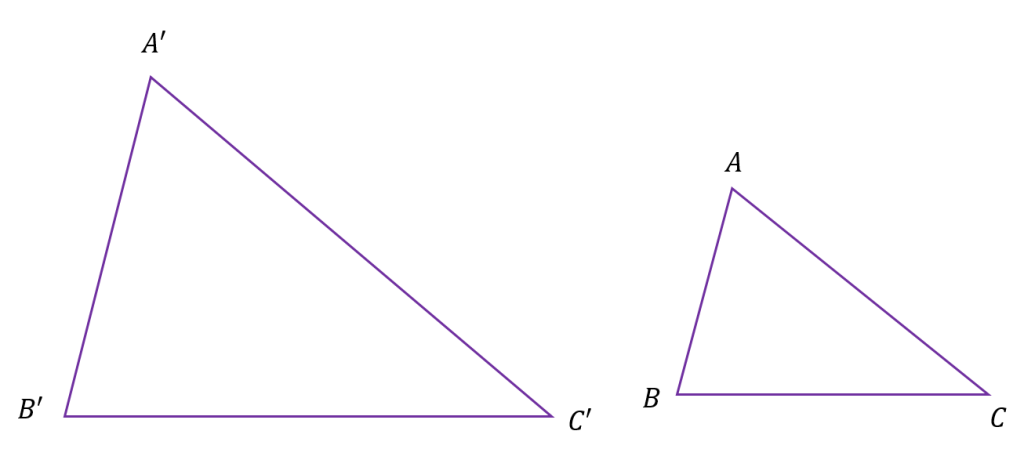
دو مثلث متشابه اند اگر و فقط اگر زوایای آنها با هم برابر باشند.

در شکل بالا اگر سه زاویه دو مثلث دو به دو با هم برابر باشند ، نسبت تشابه به صورت زیر نوشته می شود:

$\hat{A}=\hat{A^{'}}\,\,,\,\,\hat{B}=\hat{B^{'}}\,\,,\,\,\hat{C}=\hat{C^{'}}$

$\rightarrow \,\,\, \frac{A^{'}B^{'}}{AB}=\frac{A^{'}C^{'}}{AC}=\frac{B^{'}C^{'}}{BC}$

$\leftrightarrow \,\,\, \triangle {A^{'}B^{'}C^{'}} \sim \triangle{ABC}$

در ادامه چند نکته درباره تشابه دو مثلث می بینیم:

هرگاه دو زاویه از مثلثی با دو زاویه از مثلثی دیگر برابر باشند، آن دو مثلث متشابه اند.

هرگاه یک زاویه تند از مثلث قائم الزاویه با یک زاویه تند از مثلث قائم الزاویه دیگر برابر باشند آنگاه دو مثلث قائم الزاویه متشابه اند.

در هر مثلث نسبت اندازه های هر دو ضلع با عکس نسبت ارتفاع های وارد بر آن ها برابر است.

قضیه 1: هرگاه دو زاویه از مثلثی ، با دو زاویه از مثلث دیگر هم اندازه باشند دو مثلث متشابه اند. مثلا در دو مثلث شکل بالا داریم:

$\hat{B}=\hat{B^{'}}\,\,,\,\,\hat{C}=\hat{C^{'}}$

$\rightarrow \triangle { A^{'}B^{'}C^{'}} \sim \triangle{ABC}$

قضیه 2: هرگاه اندازه های دو ضلع از مثلثی با اندازه های دو ضلع از مثلث دیگر متناسب باشند و زاویه بین آنها هم اندازه باشند دو مثلث متشابه اند. مثلا در دو مثلث شکل بالا داریم:

$\hat{A}=\hat{A^{'}}\,\,,\,\,\frac{A^{'}B^{'}}{AB}=\frac{A^{'}C^{'}}{AC}$

$\rightarrow \triangle { A^{'}B^{'}C^{'}} \sim \triangle{ABC}$

قضیه 3: هرگاه اندازه های سه ضلع از مثلثی با اندازه های سه ضلع از مثلث دیگر متناسب باشند دو مثلث متشابه اند. مثلا در دو مثلث شکل بالا داریم:

$\frac{A^{'}B^{'}}{AB}=\frac{A^{'}C^{'}}{AC}= \frac{B^{'}C^{'}}{BC}$

$\rightarrow \triangle { A^{'}B^{'}C^{'}} \sim \triangle{ABC}$

نکته: در نوشتن نسبت اضلاع باید به این نکات توجه کرد که فقط اضلاع رو برو به زاویه های برابر باهم متناسب اند.

قضیه اساسی تشابه مثلث ها

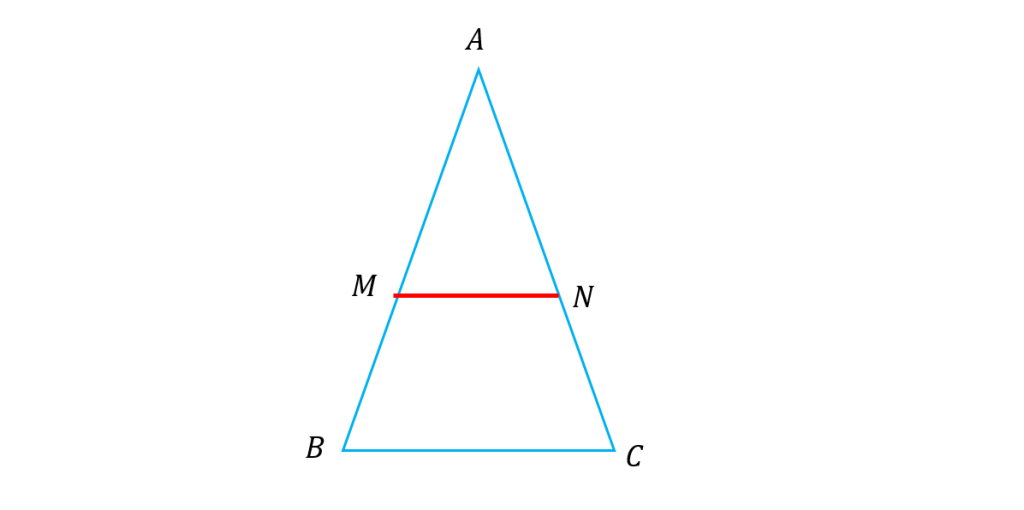
اگر خط راستی موازی یکی از اضلاع مثلثی ، دو ضلع دیگر (یا امتداد آنها) را در دو نقطه قطع کند مثلثی با آنها تشکیل می دهد که با مثلث اصلی متشابه است. در شکل زیر این موضوع نمایش داده شده است:

$MN\parallel BC \,\,\,\rightarrow\,\,\, \triangle { AMN} \sim \triangle{ABC}$

قضیه تالس را با رسم شکل تعریف کنید.

هرگاه در یک مثلث، خطی موازی یکی از اضلاع، دو ضلع دیگر مثلث را در دو نقطه قطع کند، روی آن دو ضلع، چهار پاره خط جدا می کند که اندازه های آنها تشکیل یک تناسب را می دهند. به طور خلاصه هر گاه مانند شکل زیر داشته باشیم $DE \parallel BC$ آنگاه $\frac{AD}{DB}=\frac{AE}{EC}$

تعمیم قضیه تالس چگونه انجام می شود؟

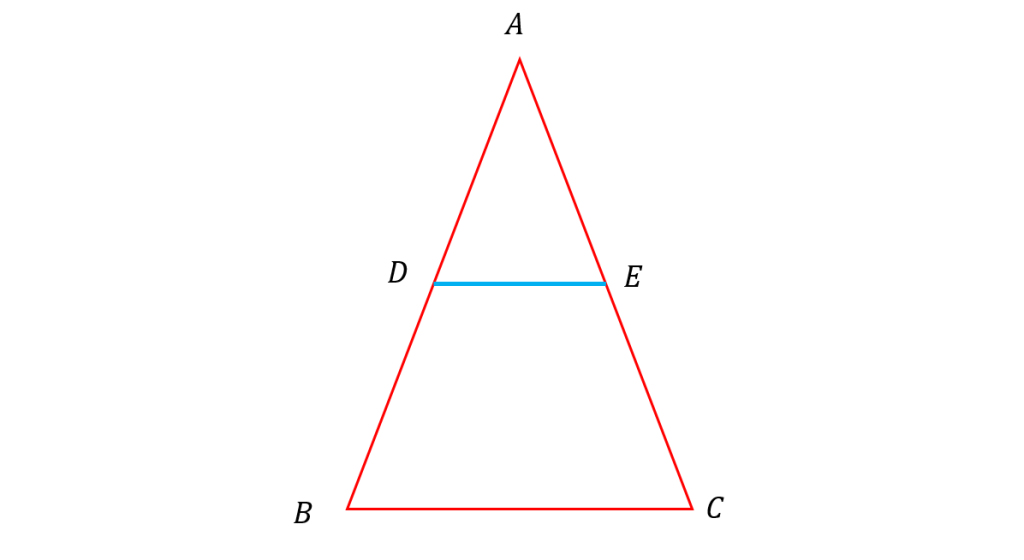
اگر خطی دو ضلع مثلثی را در دو نقطه قطع کند و با ضلع سوم آن موازی باشد ، مثلثی پدید می آید که اندازه ضلع های آن با اندازه ضلع های مثلث اصلی متناسب اند. مثلا در شکل بالا داریم :

$\frac{AD}{AB}=\frac{AE}{AC}=\frac{DE}{BC}$

آیا عکس قضیه تالس خودش یک قضیه است؟

عکس قضیه تالس نیز خودش یک قضیه است مثلا در شکل بالا اگر خطی مانند $DE$ دو ضلع مثلثی مانند $ABC$ را قطع کند و روی آنها چهار پاره خط با اندازه های متناظرا متناسب جدا کند یعنی $\frac{AD}{DB}=\frac{AE}{EC}$ آن گاه خط رسم شده با ضلع سوم مثلث موازی است یعنی $DE\oparallel BC$ .

آیا در ذوزنقه هم قضیه تالس برقرار است؟

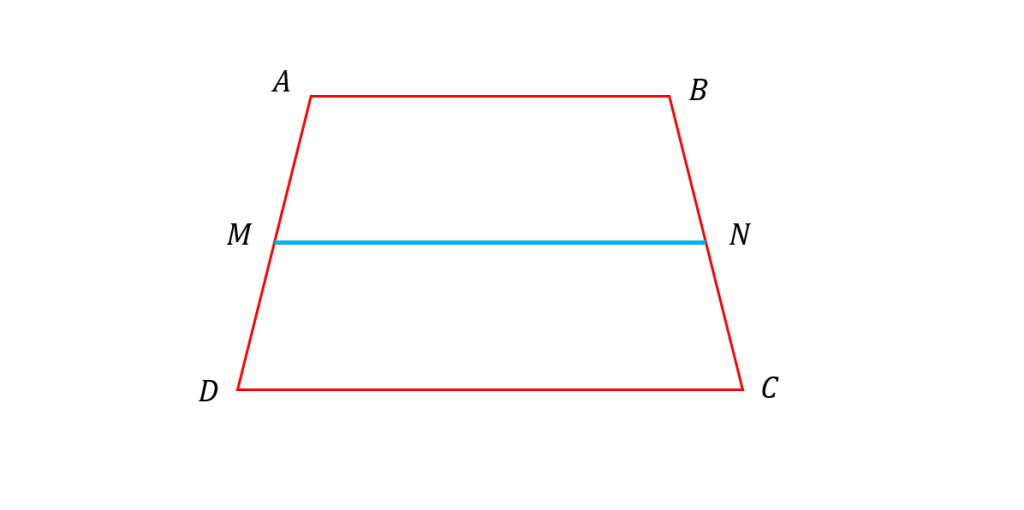
در ذوزنقه زیر $MN\parallel AB\parallel CD$ برقرار است بنابراین می توان برای این ذوزنقه هم قضیه تالس را برقرار دانست پس داریم:

$\frac{AM}{MD}=\frac{BN}{NC}$

قضیه تالس و تشابه در مثلث ها چه اثری در محیط و مساحت دو شکل دارند؟

می دانیم اگر دو شکل متشابه باشند آنگاه نسبت اضلاع نظیر آنها برابر با نسبت تشابه است. نسبت اجزای فرعی دو شکل متشابه مانند محیط ها و مساحت های شکل را نیز می توان بدست آورد.

قضیه: هرگاه دو مثلث متشابه باشند آنگاه نسبت اندازه های هر دو جز متناظر (ارتفاع ها، میانه ها، نیمساز ها و محیط ها) مساوی نسبت تشابه و نسبت مساحت های آنها مساوی توان دوم (مجذور یا مربع) نسبت تشابه است.

هرگاه دو چند ضلعی با نسبت تشابه $K$ متشابه باشند، نسبت محیط های آنها، $k$ است. نسبت مساحتهای آنها $k^{2}$ است.

هر دو $n$ ضلعی منتظم همواره با هم متشابه اند.

جمع بندی

در این مقاله به بیان نسبت و تناسب و خواص آن پرداختیم. چراکه اگر دو چند ضلعی متشابه باشند آنگاه نسبت اضلاع آنها مقدار ثابتی است که نسبت تشابه نام دارد. در این مقاله بیان کردیم که چه موقع دو شکل از جمله مثلث با هم متشابه اند. شرایط تشابه دو مثلث متساوی الاضلاع، مثلث قائم الزاویه و هر مثلث دلخواه را بیان کردیم. همچنین در این مقاله قضیه اساسی تشابه مثلث ها و قضیه تالس آموزش داده شده است. در ادامه تعمیم قضیه تالس و عکس آن هم بیان شده است. در نهایت با بیان کاربردهایی از قضیه تالس و تشابه مثلث ها این مقاله را به پایان رساندیم. لطفا ما را از نظرات ارزشمند خود در مورد مقاله تشابه و تالس بهره مند کنید.

همه چیز درباره ی تشابه اشکال هندسی، مثلث و قضیه تالس را دراین مقاله بخوانید

ویژگی اصلی دو کسر دارای نسبت و تناسب چیست؟

ویژگی های دو کسر دارای نسبت و تناسب در ریاضی چیست؟

چه موقع می گوییم دو شکل هندسی متشابه اند؟

شرایط تشابه دو مثلث چیست؟

قضیه اساسی تشابه مثلث ها

قضیه تالس را با رسم شکل تعریف کنید.

تعمیم قضیه تالس چگونه انجام می شود؟

آیا عکس قضیه تالس خودش یک قضیه است؟

آیا در ذوزنقه هم قضیه تالس برقرار است؟

قضیه تالس و تشابه در مثلث ها چه اثری در محیط و مساحت دو شکل دارند؟

دیدگاهتان را بنویسید لغو پاسخ

آخرین مطالب وبلاگ

دنباله های عددی

تابع خطی و معادله خط

تابع و دامنه و برد آن

تعیین علامت

عبارت و معادله گویا

معادله درجه دوم

معادله

عبارت جبری

قدرمطلق

دوره ها

دسترسی سریع

دسترسی سریع

مقالات مادر