جامع ترین آموزش و جمع بندی نکات درباره ی دایره محاطی ومحیطی

دایره محاطی و محیطی به ترتیب دایره ای هستند که در داخل یک شکل محاط می شود و دایره ای هستند که در دور شکل به طوری که شامل همه راس های شکل باشند محیط می شوند. در این مقاله به بیان شرایط محیطی یا محاطی بودن یک چندضلعی را به طور کلی بیان کردیم و بعد از آن به طور اختصاصی به آموزش دایره ی محاطی و محیطی در مثلث و چهارضلعی پرداختیم و همه روابطی که برای حل مسائل به آنها نیاز دارید را در این مقاله بیان کردیم.

چندضلعی های محیطی چه ویژگی هایی دارند؟

چند ضلعی را محاطی می گوییم اگر و فقط اگر دایره ای باشد که از همه رئوس آن گذرد؛ در این صورت دایره را دایرە محیطی آن چند ضلعی می نامیم.

می دانیم برای اینکه دایره ای از دو نقطه بگذرد، باید مرکز دایره روی عمود منصف پاره خطی باشد که آن دو نقطه دو سر آن است.

یک چند ضلعی، محاطی است اگر و فقط اگر عمود منصف های همه ضلع های آن در یک نقطه همرس باشند.

چند ضلعی های محیطی چه ویژگی هایی دارند؟

چند ضلعی را محیطی می گوییم اگر و فقط اگر دایره ای باشد که بر همه ضلع های آن مماس باشد؛ در این صورت دایره را دایرۀ محاطی این چند ضلعی می نامیم.

یک چند ضلعی، محیطی است اگر و فقط اگر همه نیمسازهای زاویه های آن در یک نقطه همرس باشند.این نقطه مرکز دایره محاطی چند ضلعی است.

نکته : اگر در یک $n$ ضلعی محیطی با مساحت $S$ و محیط $2P$ شعاع دایره محاطی برابر $r$ باشد داریم: $S=rP$

دایره های محیطی و محاطی مثلث دلخواه

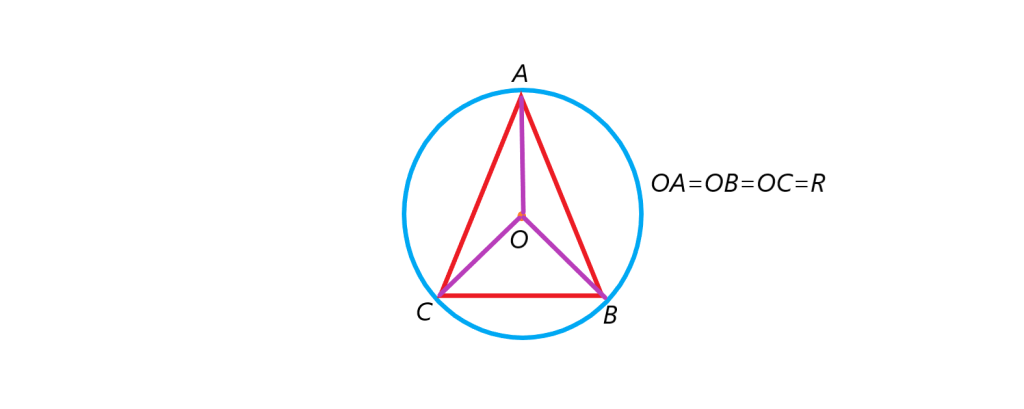
دایره محیطی مثلث: نقطه همرسی سه عمود منصف مثلث تنها نقطه ای است که از سه راس یک مثلث به یک فاصله است. دایره ای به مرکز همرسی عمود منصف اضلاع یک مثلث، دایره محیطی مثلث است. در نتیجه مثلث همواره محاطی است. چون هر نقطه روی عمودمنصف از دو سر پاره خط (که همان ضلع مثلث است) به یک فاضله است پس خطوط بنفش رنگ در شکل زیر با هم برابر و همان شعاع دایره اند.

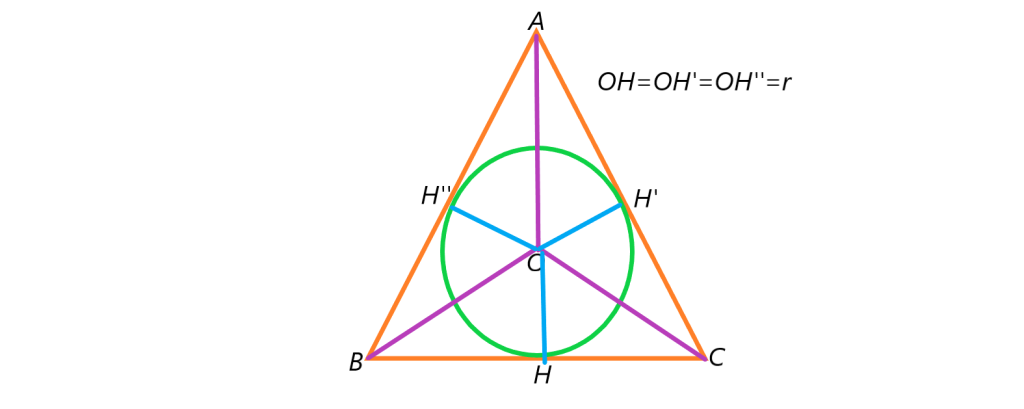
دایره محاطی مثلث: نیمساز هاس زوایای داخلی مثلث در نقطه ای درون مثلث همرس اند. دایره ای به مرکز همرسی نیمسازهای زوایای داخلی مثلث دایره محیطی مثلث است . در نتیجه مثلث همواره محیطی است. چون هر نقطه روی نیمساز از دو ضلع زاویه (که اینجا همان ضلع مثلث است) به یک فاصله است پس در شکل زیر خطوط آبی رنگ با هم برابرند و همان شعاع دایره اند.

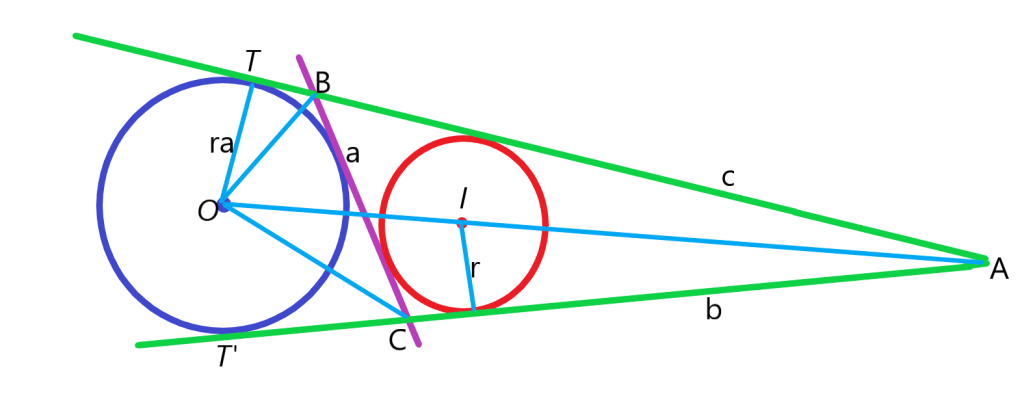
محل برخورد نیمساز زاویه $A$ از مثلث $ABC$ با نیمساز زوایای خارجی $B$ و $C$ مرکز دایره محاطی خارجی نظیر راس $A$ را می دهد. این دایره را در شکل زیر می بینید. شعاع این دایره را $r_{a}$ را می نامیم.

شعاع دایره محاطی خارجی: اگر مساحت مثلث را برابر $S$ در نظر بگیریم و محیط مثلث را برابر $2P$ در نظر بگیریم . شعاع دایره محاطی خارجی نظیر هر راس بصورت زیر بدست می آید:

$r_{a}=\frac{S}{P-a}\,\,\,,\,\,\,r_{b}=\frac{S}{P-b}\,\,\,,\,\,\,r_c=\frac{S}{P-c}$

مساحت مثلث محاطی:مساحت مثلثی محاط شده در دایره ای به شعاع $R$ برابر است با :

$\frac{3\sqrt{3}}{4}R^{2}$

شعاع دایره محاطی مثلث: اگر $r_{a}$ و $r_{b}$ و $r_{c}$ شعاع های سه دایره محاطی خارجی مثلث باشند و $r$ شعاع دایره محاطی داخلی باشد داریم:

$\frac{1}{r_{a}}+\frac{1}{r_{b}}+\frac{1}{r_{c}}=\frac{1}{r}$

شعاع دایره محاطی مثلث: اگر $h_{a}$ و $h_{b}$ و $h_{c}$ ارتفاع های مثلث باشند و $r$ شعاع دایره محاطی داخلی باشد داریم:

$\frac{1}{h_{a}}+\frac{1}{h_{b}}+\frac{1}{h_{c}}=\frac{1}{r}$

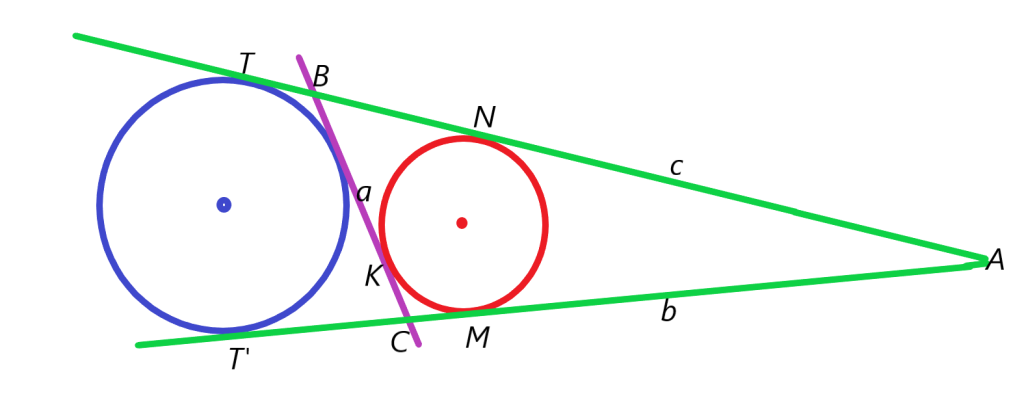
در شکل زیر اگر محیط مثلث $ABC$ برابر $2P$ باشد و $M$ و $N$ محل تماس دایره محاطی داخلی با اضلاع مثلث باشد و $T$ و $T^{'}$ محل تماس دایره محاطی خارجی با مثلث باشد آنگاه داریم:

$AM=AN=P-a$

$BN=BK=P-b$

$CM=CK=P-c$

$AT=AT^{'}=P$

نکته: عمود منصف یک ضلع هر مثلث و نیمساز زاویه مقابل به آن ضلع، یکدیگر را روی دایره محیطی مثلث قطع می‌کنند.

نکته: برخلاف مثلث همه ی چندضلعی های دیگر لزوما محیطی یا محاطی نیستند.

چه نوع چهارضلعی هایی محیطی یا محاطی اند؟

قضیه: یک چهارضلعی محاطی است، اگر و فقط اگر دو زاویه مقابل آن مکمل باشند. مثل مربع – مستطیل- ذوزنقه متساوی الساقین

قضیه: یک چهارضلعی محیطی است اگر و فقط اگر مجموع اندازه های دو ضلع مقابل برابر مجموع اندازه های دو ضلع دیگر باشند. مربع –لوزی-کایت

نکته:

چند ضلعی های منتظم هم محاطی و هم محیطی هستند.

اگر یک ذوزنقه، هم محیطی باشد و هم محاطی آنگاه مساحت این ذوزنقه برابر است با میانگین حسابی دو قاعده آن ضرب در میانگین هندسی آنها.

یک دایره به شعاع r و $n$ ضلعی های منتظم محاطی و محیطی داریم اندازه هر ضلع $n$ ضلعی محیطی برابر است با $2r\tan {\frac{180}{n}}$ و اندازه $n$ ضلعی منتظم محاطی برابر با $2r \sin {\frac{180}{n}$ است.

جمع بندی

در این مقاله به بیان دایره محیطی و محاطی و همه نکات مربوط به آن پرداختیم. شرایط اینکه یک چندضلعی محاطی یا محیطی باشد را بیان کردیم. دایره های محاطی و محیطی مثلث دلخواه را تعریف کردیم و به این ترتیب همه ی نکات و فرمول های مربوط به آنها را بیان کردیم. چهارضلعی های محیطی و محاطی و شرایط اینکه محیطی یا محاطی باشند را بیان کردیم. در نتیجه این مقاله یک آموزش جامع از نکات مربوط به دایره های محیطی و محاطی است. بنابراین لطفا ما را با نظرات خود در قسمت کامنت ها خوشحال کنید.

جامع ترین آموزش و جمع بندی نکات درباره ی دایره محاطی ومحیطی

چندضلعی های محیطی چه ویژگی هایی دارند؟

چند ضلعی های محیطی چه ویژگی هایی دارند؟

دایره های محیطی و محاطی مثلث دلخواه

چه نوع چهارضلعی هایی محیطی یا محاطی اند؟

دیدگاهتان را بنویسید لغو پاسخ

آخرین مطالب وبلاگ

دنباله های عددی

تابع خطی و معادله خط

تابع و دامنه و برد آن

تعیین علامت

عبارت و معادله گویا

معادله درجه دوم

معادله

عبارت جبری

قدرمطلق

دوره ها

دسترسی سریع

دسترسی سریع

مقالات مادر