با خواندن این مقاله همه چیز را درباره مثلث بیاموزید.

مثلث نامی است که برای سه ضلعی گذاشته شده است.در این مقاله به آموزش ارتفاع ، میانه و نیمساز مثلث می پردازیم و خواص هر کدام را بیان می کنیم. مثلث را می توان براساس زاویه هایش به سه دسته تقسیم کرد. همچنین مثلث چندین نوع دارد اما معروف ترین نوع آن مثلث متساوی الاضلاع، مثلث متساوی الساقین و قائم الزاویه هستند. در این مقاله به بررسی خواص هر کدام از آنها و روابط طولی آنها پرداختیم. همچنین روابط طولی برای مثلث و قوانین سینوس و قوانین کسینوس و قضیه هرون در این مقاله بیان شده است. این مقاله یک مقاله ی مفید برای کسانی است که علاقمند به یادگیری همه چیز در مورد مثلث هستند.

توجه: اگر نیاز به آشنایی در مورد زاویه، نیمساز ، عمود و عمودمنصف دارید لطفا به مقاله هندسه تحلیلی مراجعه کنید. همچنین اگر آشنایی با سینوس و کسینوس ندارید حتما به مقاله های مثلثات سر بزنید.

مثلث چه نوع شکلی است؟

به شکل بسته سه ضلعی مثلث می گویند. در واقع مثلث یک چندضلعی با سه ضلع است.

مثلث علاوه بر سه ضلع، سه زاویه هم دارد. محل برخورد هر دو ضلع یک نقطه است که راس نام دارد.

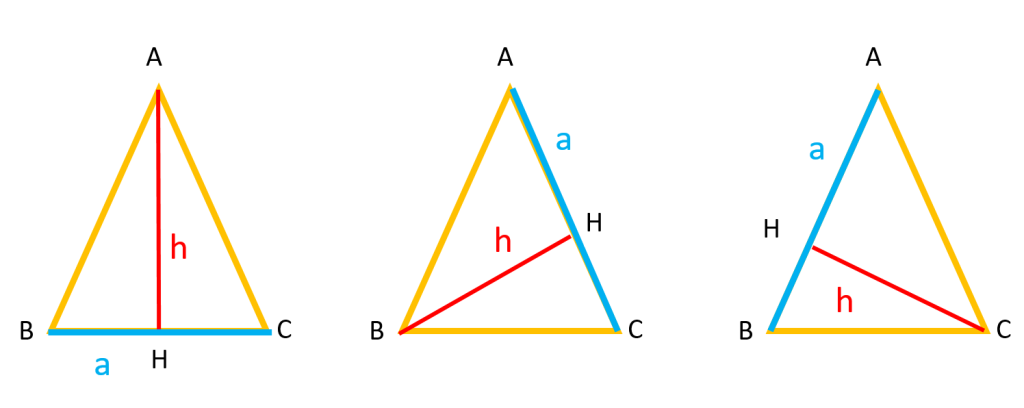
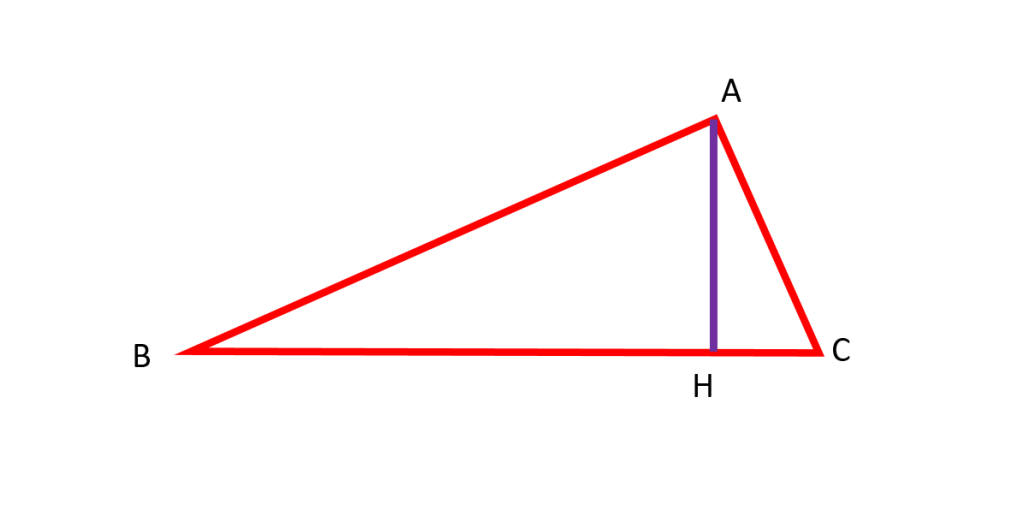
ارتفاع: از هر راس مثلث می توان بر ضلع روبروی آن راس، عمودی رسم کرد به این عمود ها ارتفاع های مثلث می گویند و به ضلعی که ارتفاع بر آن فرود آمده است قاعده ی مثلث می گویند به این ترتیب هر مثلث سه ارتفاع و سه قاعده دارد. در شکل زیر این سه حالت را می بینید:

در هر مثلث ارتفاع ها همرس اند یعنی اگر هر سه ارتفاع را همزمان رسم کنیم همدیگر را در یک نقطه قطع می کنند.

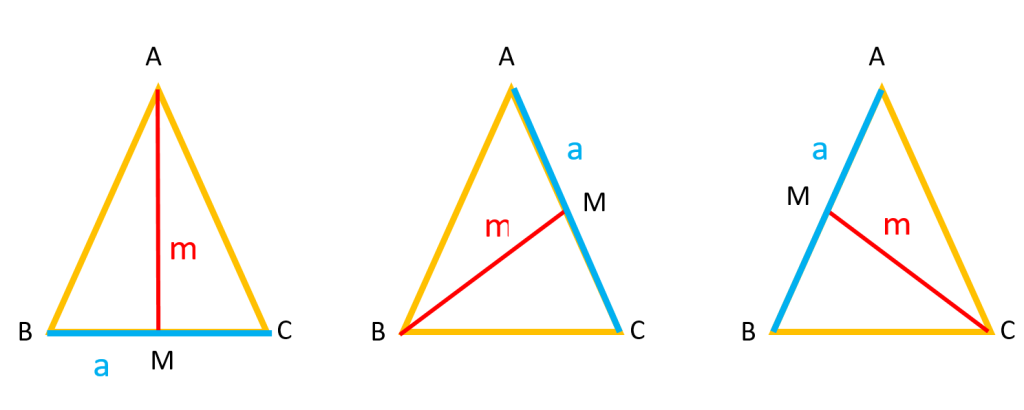
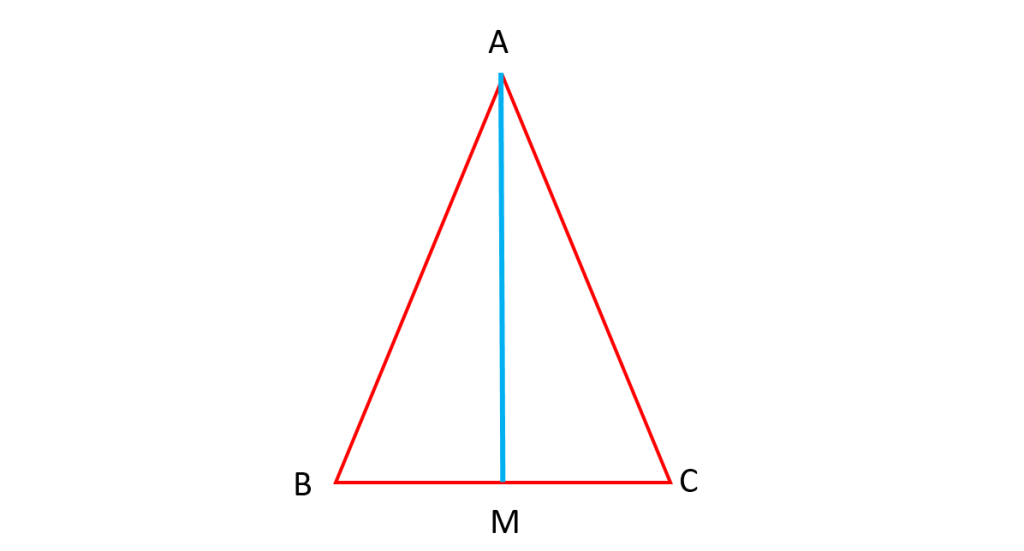
میانه: اگر هر راس مثلث را به وسط ضلع مقابلش وصل کنیم میانه مثلث را رسم کرده ایم از آنجا که هر مثلث سه راس و سه ضلع دارد بنابراین سه میانه هم دارد. در شکل زیر سه حالت از میانه را می بینید:

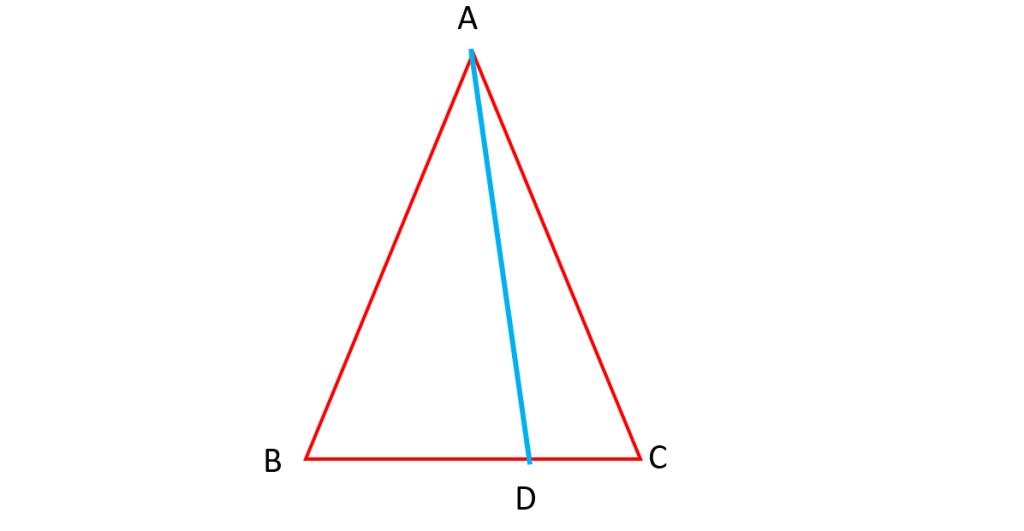
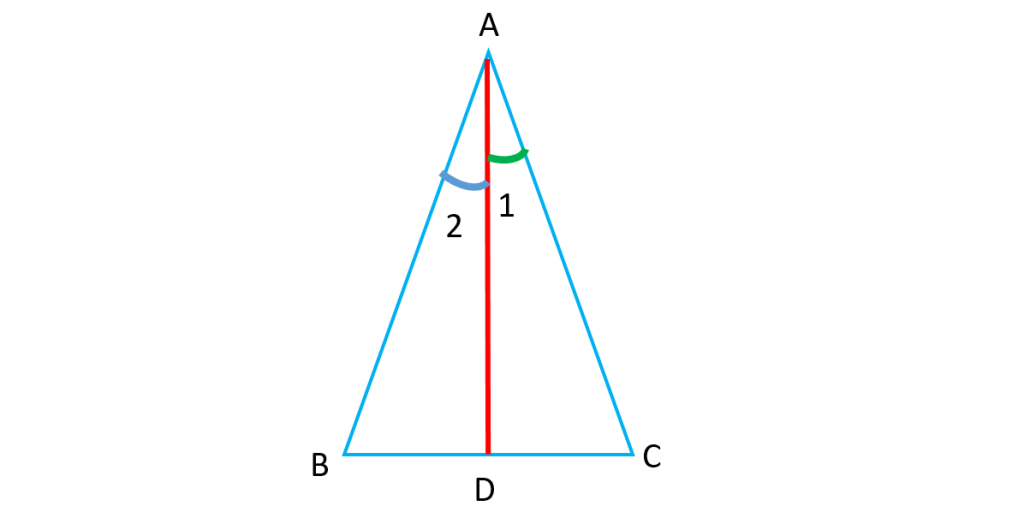
نیمساز: اگر برای هر زاویه از مثلث نیمساز را رسم کنیم می بینیم که در هر مثلث نیمسازها همرس اند.

عمودمنصف: اگر برای هر ضلع از مثلث یک عمود منصف رسم کنید این سه عمودمنصف برای هر مثلث همرس اند.

در هر مثلث، اندازه هر زاویه خارجی برابر با مجموع دو زاویه داخلی غیر مجاور آن است. بنابراین هر زاویه خارجی مثلث از هر زاویه داخلی غیرمجاورش بزرگتر است.

مجموع زوایای داخلی مثلث 180 درجه است.

اگر اندازه دو زاویه از یک مثلث را بدانیم اندازه زاویه سوم هم بدست می آید چون مجموع زوایای مثلث برابر 180 درجه است.

سه میانه هر مثلث در نقطه ای درون آن مثلث همرس اند به طوری که فاصله این نقطه تا وسط هر ضلع برابر ثلث اندازه میانه نظیر این ضلع است. و فاصله اش تا هر راس برابر دو برابر ثلث اندازه میانه نظیر آن راس است.

در هر مثلث مجموع اندازه های هر دو ضلع از ضلع سوم بزرگتر است.

اگر در یک مثلث دو زاویه نابرابر باشد، ضلع روبرو به زاویه بزرگتر، بزرگتر است از ، ضلع روبرو به زاویه کوچکتر.

اگر در مثلثی دو ضلع نابرابر باشند زاویه روبرو به ضلع بزرگتر، بزرگتر است از زاویه روبرو به ضلع کوچکتر .

چند نوع مثلث داریم؟

مثلث ها با توجه به اندازه زاویه هایشان به سه دسته تقسیم می کنیم :

مثلث هایی که هر سه زاویه آنها تند است.

مثلث هایی که یک زاویه راست دارند.

مثلث هایی که یک زاویه باز دارند.

نکته: محل برخورد عمودمنصف های مثلث ممکن است داخل مثلث باشد ( اگر هر سه زاویه مثلث تند باشند) یا ممکن است روی یکی از اضلاع مثلث باشد (در مثلث قائم الزاویه محل برخورد عمودمنصف ها وسط وتر است) یا ممکن است خارج از مثلث باشد (اگر مثلث یک زاویه باز داشته باشد)

یک سری از مثلث ها به علت یک سری از خواص نام مشخصی دارند. در ادامه به توضیح شکل و خواص هر کدام می پردازیم.

مثلث متساوی الاضلاع: برخی از مثلث ها هر سه ضلع شان با هم برابرند. به این مثلث ها مثلث متساوی الاضلاع می گویند. در این مثلث ها هر سه زاویه نیز با هم برابرند و از آنجاکه مجموع زوایای داخلی هر سه ضلعی (با توجه به آنچه در مقاله چندضلعی ها خواندیم) برابر 180 درجه است پس در مثلث متساوی الاضلاع هر زاویه از مثلث 60 درجه است. در مثلث متساوی الاضلاع ارتفاع و میانه و نیمساز هر سه بر هم منطبق اند. در شکل زیر $BE$ و $AD$ و $CF$ هر سه هم ارتفاع هم نیمساز و هم میانه هستند.

$A=B=C=60$

$AB=AC=BC$

$BE=AD=CF$

در مثلث متساوی الاضلاع یک پاره خط نیمساز است؛ اگر و تنها اگر میانه باشد.

مجموع فاصله های هر نقطه دلخواه درون مثلث متساوی الاضلاع از اضلاع مثلث برابر با ارتفاع این مثلث است.

مثلث متساوی الاضلاع سه خط تقارن دارد.

مثلث متساوی الساقین: برخی از مثلث ها فقط دو ضلع شان با هم برابر است به این دو ضلع ساق می گویند و به ضلعی که اندازه اش با این دو ضلع متفاوت است قاعده می گویند. در مثلث متساوی الساقین دو زاویه مجاور به قاعده با هم برابرند. به راسی از مثلث که محل برخورد دو ساق است زاویه راس می گویند. ارتفاع میانه و نیمسازی که از زاویه راس می گذرد برهم منطبق اند. در مثلث متساوی الساقین زیر $AB=AC$ و $B=C$ و $AD$ نیمساز، میانه و ارتفاع است.

نکته: مثلث متساوی الساقین یک خط تقارن دارد. که خط تقارن همان میانه و ارتفاع و عمود منصف وارد بر قاعده و نیمساز زاویه راس است.

در یک مثلث دو ضلع برابرند؛ اگر و تنها اگر زاویه های روبه رو به آنها باهم برابر باشند. (اگر و تنها اگر یک اصطلاح در گزاره دو شرطی است که می توانید در مقاله گزاره از این مطلب آگاهی بیشتری میابید)

نکته: در هر مثلث متساوی الساقین مجموع فاصله های هر نقطه روی قاعده از دو ساق، برابر با ارتفاع وارد هر ساق مثلث است.

نکته: در هر مثلث متساوی الساقین قدرمطلق تفاضل فاصله های هر نقطه روی امتداد قاعده از ساق ها برابر اندازه ارتفاع وارد بر ساق است.

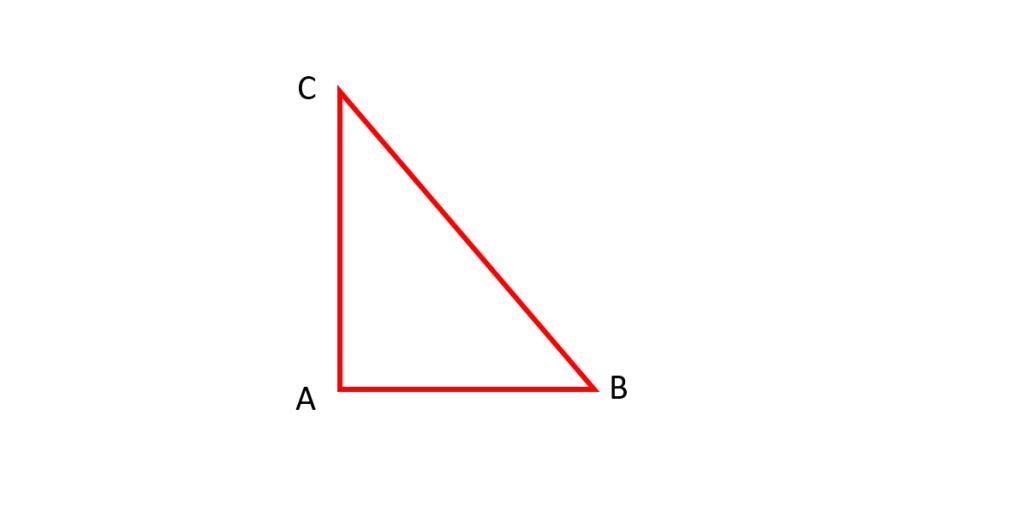
مثلث قائم الزاویه: در این مثلث یک زاویه قائمه وجود دارد ( اگر علاقمند به یادگیری در مورد انواع زاویه ها هستید به مقاله هندسه تحلیلی مراجعه کنید) به ضلع روبروی زاویه قائمه وتر می گویند. در شکل زیر داریم: $A=90$ و $B+C=90$ و $BC$ وتر است.

چگونه مساحت یک مثلث را بدست آوریم؟

برای دانستن فرمول مساحت مثلث لطفا به مقاله ی محیط و مساحت مراجعه کنید.

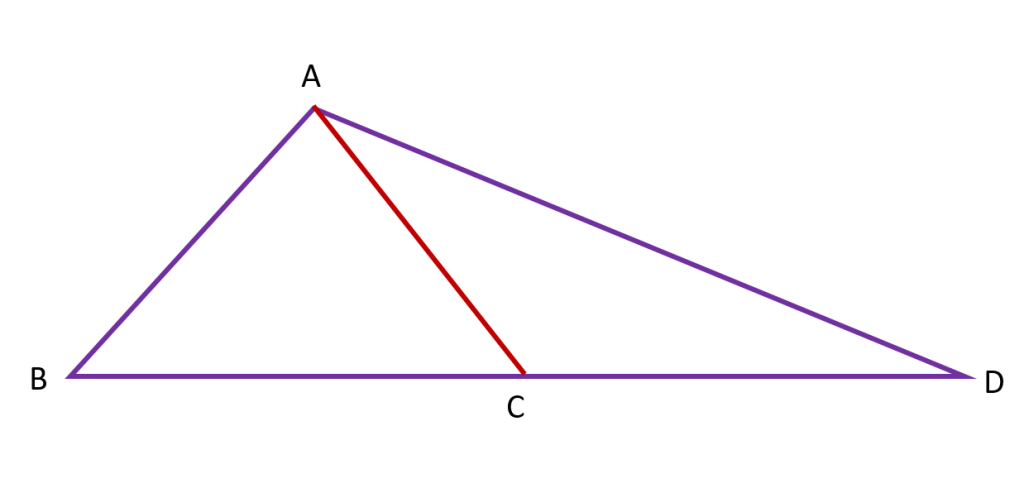
نکته: اگر دو مثلث در یک رأس مشترک بوده و قاعدۀ مقابل به این رأس آنها روی یک خط راست باشد، نسبت مساحتهای آنها برابر با نسبت اندازۀ قاعده های آنهاست. چون ارتفاع این دو مثلث با هم برابر است. مثلا در شکل زیر که دو مثلث $ABC$ و $ACD$ که در راس $A$ مشترک اند نسبت مساحت هایشان به صورت زیر بدست می آید:

$\frac{S_{ABC}}{S_{ACD}}=\frac{BC}{CD}$

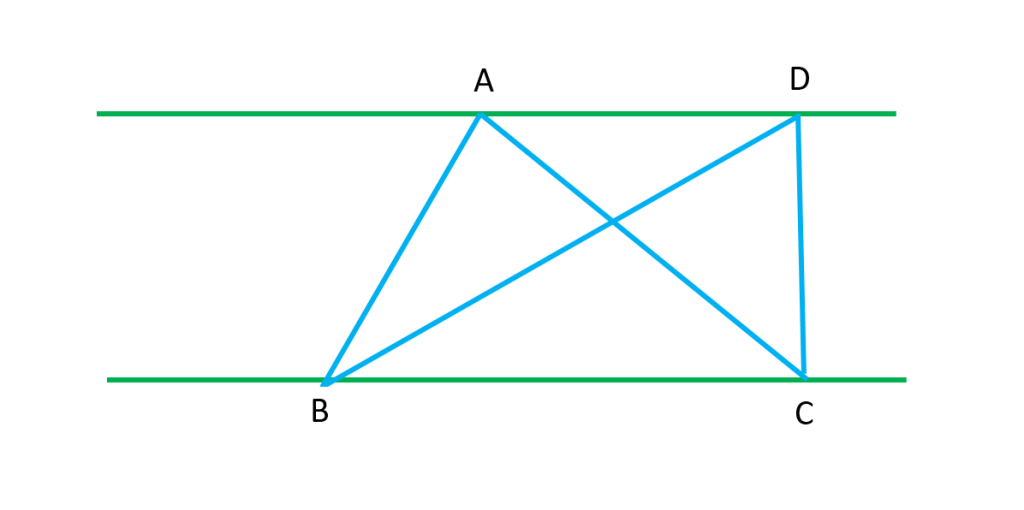
نکته: اگر دو مثلث، قاعدۀ مشترکی داشته باشند و رأس های روبه روی این قاعدۀ آنها، روی یک خط، موازی این قاعده باشند، این مثلث ها هم مساحت اند. مثلا در شکل زیر مثلث های $ABC$ ، $DBC$ هم مساحت اند. چون هم ارتفاع هایشان با هم برابر است هم قاعده های نظیر این ارتفاع ها است.

در ادامه چند نکته درباره نسبت مساحت های دو مثلث می خوانیم:

هرگاه اندازۀ ارتفاع های دو مثلث برابر باشد، نسبت مساحت های آنها برابر با نسبت اندازۀ قاعده هایی است که این ارتفاع ها بر آنها وارد شده است.

در دو مثلث اگر اندازه قاعده ها با هم برابر باشند نسبت مساحت ها برابر نسبت اندازه ارتفاع های متناظر با این دو قاعده است.

اگر دو ضلع از یک مثلث با هم برابر باشند، آنگاه ارتفاع های وارد بر آن دو ضلع نیز با هم برابرند.

با توجه به فرمول مساحت، در هر مثلث نسبت اندازه های هر دو ضلع، با عکس نسبت ارتفاع های وارد بر آنها برابر است.

در هر مثلث متساوی الاضلاع اندازه ارتفاع رادیکال سه دوم ضلع و اندازه مساحت برابر رادیکال سه چهارم مجذور ضلع است.یعنی اگر اندازه ضلع مثلث متساوی الاضلاع برابر $a$ باشد داریم:

$h=\frac{\sqrt{3}}{2}a\,\,\,,\,\,\,S=\frac{\sqrt{3}}{2}a^{2}$

اگر وسط های سه ضلع هر مثلث را به هم متصل کنیم چهار مثلث حاصل هم نهشت و درنتیجه هم مساحت هستند.

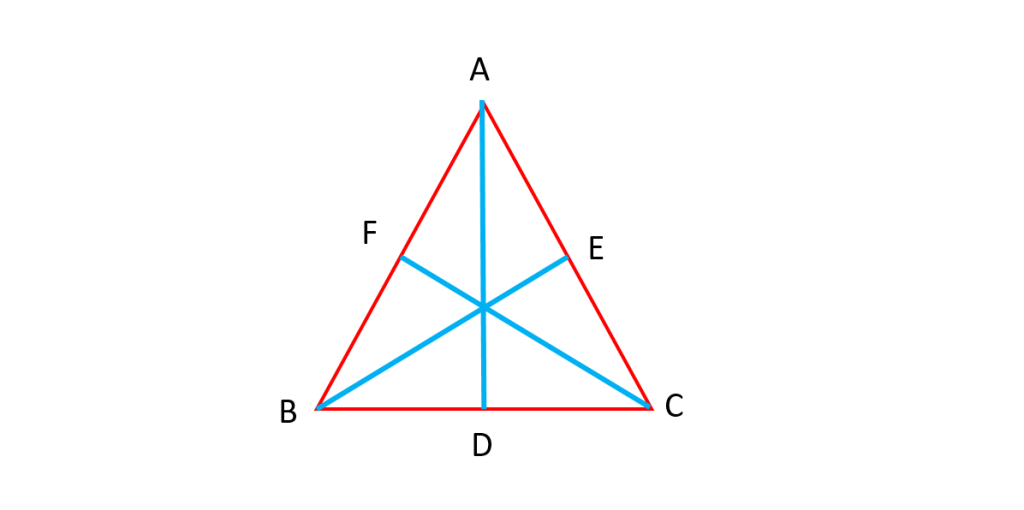
میانه های هر مثلث آن را به شش قسمت با مساحت های برابر تقسیم می کند.

اگر دو ضلع از یک مثلث با هم برابر باشند آنگاه ارتفاع های وارد بر آن دو ضلع نیز با هم برابرند. و برعکس اگر دو ارتفاع از یک مثلث با هم برابر باشند آنگاه اضلاع نظیر به آن ارتفاع ها نیز با هم برابرند.

در یک مثلث دو ضلع با هم برابرند اگر و تنها اگر ارتفاع های نظیر آنها با هم برابر باشند.

رابطه ی فیثاغورس در مثلث قائم الزاویه چه رابطه ای است؟

رابطه میان مجذور ( مربع ) اندازه ضلع های مثلث قائم الزاویه به رابطه ی فیثاغورس معروف است. این رابطه بیان می کند که در هر مثلث قائم الزاویه، مجذور وتر با مجموع مجذور های دو ضلع دیگر برابر است

$b^{2}+c^{2}=a^{2}$

برعکس این رابطه هم درست است یعنی اگر در مثلثی مجذور یک ضلع با مجموع مجذور دو ضلع دیگر برابر باشد ، آن مثلث قطعا قائم الزاویه است

چه روابط طولی ای در مثلث قائم الزاویه وجود دارد؟

در ادامه چند نکته درباره مثلث قائم الزاویه می خوانیم:

در هر مثلث قائم الزاویه، ارتفاع وارد بر وتر آن را به دو مثلث قائم الزاویه تفکیک می کند که هر دو با هم و با مثلث اصلی متشابه اند.

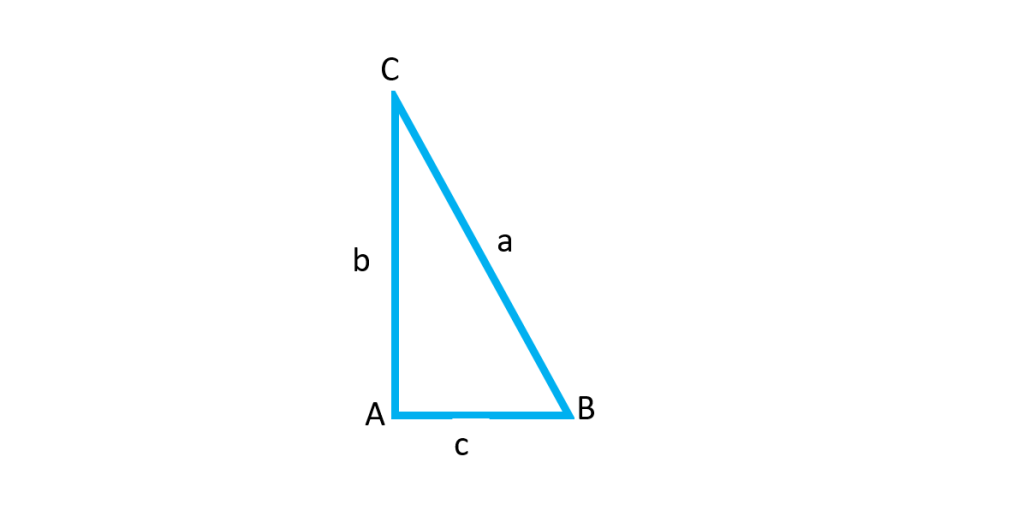
در مثلث قائم الزاویه $ABC$ روابط مهم زیر برقرارند. این رابطه ها را روابط طولی می نامیم زیرا با اندازه های اضلاع سروکار دارند:

با توجه به شکل بالا می توانیم روابط زیر را برای مثلث قائم الزاویه داشته باشیم:

$AB^{2}=BC.BH$

$AC^{2}=BC.CH$

$AB^{2}+AC^{2}=BC^{2}$

$AH^{2}=BH.CH$

$AH.BC=AB.AC$

$\frac{1}{AH^{2}}=\frac{1}{AC^{2}}+\frac{1}{AB^{2}}$

همچنین نکات زیر نیز درباره ی مثلث قائم الزاویه صدق می کند:

در هر مثلث قائم الزاویه میانه وارد بر وتر نصف وتر است. و برعکس اگر در مثلثی اندازه میانه وارد بر یک ضلع نصف اندازه آن ضلع بود آن مثلث قائم الزاویه است و آن ضلع وتر مثلث است.

در مثلث قائم الزاویه ضلع مقابل زاویه 30 درجه نصف وتر است. ( با توجه به آنچه در مثلثات خواندیم)

در مثلث قائم الزاویه ضلع مقابل زاویه 60 درجه $\frac{\sqrt{3}}{2}$ وتر است.

در مثلث قائم الزاویه ضلع مقابل زاویه 45 درجه $\frac{\sqrt{2}}{2}$ وتر است.

در مثلث قائم الزاویه با زاویه 15 درجه اندازه ارتفاع وارد بر وتر ربع وتر است.

در هر مثلث قائم الزاویه نسبت اندازه هر ضلع به سینوس زاویه مقابل به آن برابر است با اندازه وتر مثلث.

قطر دایره محیطی مثلث قائم الزاویه همان وتر مثلث است.

چه روابط طولی ای برای مثلث دلخواه وجود دارد؟

به طور کلی در همه ی مثلث ها برخی روابط بین ضلع ها و زاویه های مثلث برقرار است در ادامه به برخی از مهم ترین روابط اشاره می کنیم.

قضیه سینوس ها

در مثلث $ABC$ با اضلاع $BC=a\,\,\,,\,\,\,AC=b\,\,\,,\,\,\,AB=c$

داریم : $\frac{a}{\sin{A}}=\frac{b}{\sin{B}}=\frac{c}{\sin{C}}=2R$

که $R$ شعاع دایره محیطی است .

قضیه کسینوس ها

در مثلث دلخواه $ABC$ با اضلاع $AB=c$ و $AC=B$ و $BC=a$ ، مربع اندازه هر ضلع برابر است با مجموع مربع های اندازه های دو ضلع منهای دو برابر حاصل ضرب اندازه ی آن دو ضلع در کسینوس زاویه بین آنها :

$a^{2}=b^{2}+c^{2}-2bc\cos{A}$

$b^{2}=a^{2}+c^{2}-2ac\cos{B}$

$c^{2}=b^{2}+a^{2}-2ab\cos{C}$

قضیه میانه ها

در مثلث شکل زیر $AM$ میانه است و داریم :

$b^{2}+c^{2}=2AM^{2}+\frac{a^{2}}{2}$

قضیه استوارت

در مثلث $ABC$ شکل زیر نقطه دلخواه $D$ روی ضلع $BC$ مفروض است داریم:

$AB^{2}.DC+AC^{2}.DB=$

$AD^{2}.BC+DB.DC.BC$

قضیه نیمساز های زوایای داخلی

در هر مثلث نیمساز هر زاویه داخلی ضلع روبرو به آن زاویه را به نسبت اندازه های ضلع های آن زاویه تقسیم می کند.

$A_{1}=A_{2}\,\,\,\Rightarrow\,\,\,\frac{AB}{AC}=\frac{BD}{CD}$

محاسبه طول نیمسازهای زوایای داخلی مثلث

در هر مثلث مربع اندازه ی هر نیمساز داخلی برابر است با حاصل ضرب اندازه دو ضلع زاویه منهای حاصل ضرب اندازه دو قطعه ای که نیمساز روی ضلع مقابل ایجاد می کند.

$AD^{2}=AB.AC-BD.CD$

قضیه هرون

مساحت مثلث دلخواه $ABC$ در حالی که محیط مثلث برابر $2P$ می باشد برابر است با:

$S=\sqrt{P(P-a)(P-b)(P-c)}$

مساحت هر مثلث برابر است با نصف حاصل ضرب اندازه های هر دو ضلع در سینوس زاویه بین آنها:

$S_{ABC}=\frac{1}{2}bc\sin{A}=$

$\frac{1}{2}ab\sin{C}=\frac{1}{2}ac\sin{B}$

نکته: طول نیمساز $AD$ در مثلث $ABC$ شکل زیر برابر است با :

$AD=\frac{2AC.AB\cos{\frac{A}{2}}}{AC+AB}$

نکته:در مثلث بالا با شرایط مختلف برای زاویه $A$ شرایط متفاوتی برای اندازه اضلاع بدست می آید داریم:

$A >90\,\, \Longleftrightarrow\,\,a^{2} > b^{2}+c^{2}$

$A <90\,\, \Longleftrightarrow\,\,a^{2} < b^{2}+c^{2}$

$A=90\,\, \Longleftrightarrow\,\,a^{2}=b^{2}+c^{2}$

جمع بندی

در این مقاله به بررسی مثلث، خواص مثلث و انواع آن بیان شده است. ارتفاع، میانه و نیمساز هر مثلث و روابط مربوط به آنها بیان شده است. مساحت مثلث، قضیه فیثاغورس، قضیه سینوس ها، قضیه کسینوس ها، قضیه میانه ها، قضیه استوارت، قضیه هرون و قضیه نیمسازها در این مقاله آموزش داده شده است. اگر می خواهید درمورد همنهشتی مثلث ها بدانید لطفا به مقاله همنهشتی مراجعه کنید. اگر می خواهید درباره تشابه مثلث ها بدانید به مقاله ی مربوطه مراجعه کنید. و اگر می خواهید همه ی نکات مربوط به دایره محاطی و محیطی مثلث را بدانید به مقاله ی دایره محاطی و محیطی رجوع کنید. لطفا نظر خود را در مورد مقاله ی مثلث در قسمت کامنت ها بیان کنید.

با خواندن این مقاله همه چیز را درباره مثلث بیاموزید.

مثلث چه نوع شکلی است؟

چند نوع مثلث داریم؟

چگونه مساحت یک مثلث را بدست آوریم؟

رابطه ی فیثاغورس در مثلث قائم الزاویه چه رابطه ای است؟

چه روابط طولی ای در مثلث قائم الزاویه وجود دارد؟

چه روابط طولی ای برای مثلث دلخواه وجود دارد؟

دیدگاهتان را بنویسید لغو پاسخ

آخرین مطالب وبلاگ

دنباله های عددی

تابع خطی و معادله خط

تابع و دامنه و برد آن

تعیین علامت

عبارت و معادله گویا

معادله درجه دوم

معادله

عبارت جبری

قدرمطلق

دوره ها

دسترسی سریع

دسترسی سریع

مقالات مادر