هر آنچه لازم است درمورد بردارها، جمع، تفریق، ضرب آنها و متوازی السطوح بدانید
بردارها پاره خط های جهت داری هستند که در نشان دادن برخی کمیت های فیزیکی مثل جابجایی، سرعت و نیرو به ما کمک می کنند از این رو دانستن اطلاعات بیشتر در مورد این مبحث ریاضی به ما در یادگیری سایر علوم کمک می کند. در این مقاله به آموزش تمام نکات لازم برای آموزش بردارها می پردازیم اگر می خواهید هر آنچه که درباره بردارها لازم است بدانید و همه تمام نکات در مورد بردارها را یکجا بخوانید این مقاله را از دست ندهید. در این مقاله ابتدا به بررسی بردارها در فضای دو بعدی می پردازیم و بعد به سراغ بردارها در فضای سه بعدی می پردازیم. در هر دو حالت جمع و تفریق بردارها، قرینه بردارها، بردارهای مساوی و ضرب عدد در بردار را بررسی می کنیم. در فضای سه بعدی با چند مفهوم جدید مانند ضرب داخلی بردارها، ضرب خارجی بردارها، تصویر قائم یک بردار بر یک بردار دیگر و در نهایت حجم متوازی السطوح آشنا می شویم و تمام نکات مربوط به آنها را بیان می کنیم.
بردارها در فضای دو بعدی چگونه هستند؟
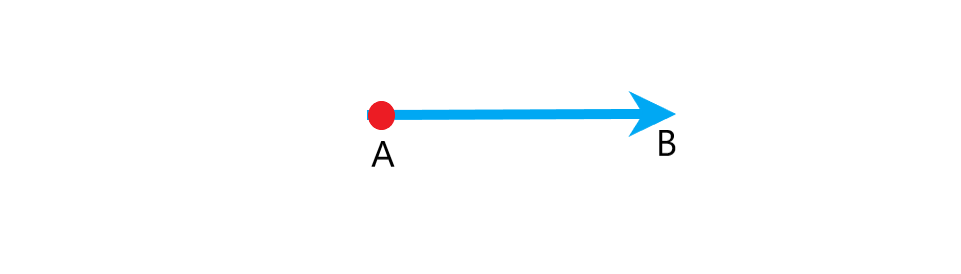
هر پاره خط جهت دار مانند یک بردار را مشخص می کند که ابتدای آن
و انتهای آن
می باشد این بردار را با
و اندازه آن را با
نشان می دهند.
اغلب جهت سهولت بردارها را با حروف کوچک لاتین مانند و اندازه آن را با
نشان می دهند.
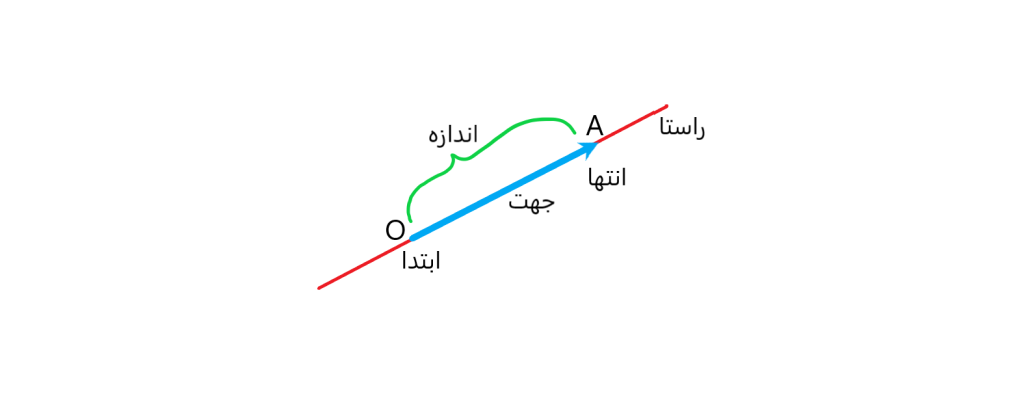
بردار را در شکل زیر در نظر بگیرید. همانطور که در این شکل نشان داده شده هر بردار سه خصوصیت دارد. راستا، اندازه و جهت بردار سه خصوصیت بردار است.
به ابتدای بردار و به
انتهای بردار می گویند. نوک پیکان جهت بردار را نشان می دهد و خطی که بردار روی آن قرار دارد راستای بردار را نشان می دهد.
چه موقع دو بردار با هم قرینه اند؟
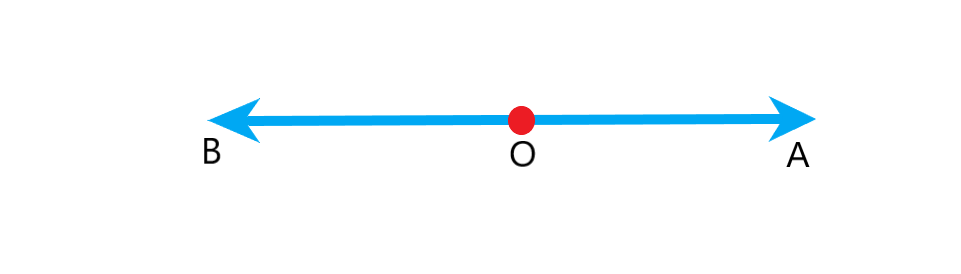
دو بردار که هم راستا و هم اندازه اند اما جهت هایشان برعکس یکدیگر است بردار های قرینه می گویند. شکل زیر دو بردار و
قرینه یکدیگرند:
بردارهای همسنگ یا مساوی چه ویژگی هایی دارند؟
دو بردار که هم راستا و هم اندازه و هم جهت اند بردارهای مساوی نام دارند. به طور کلی دو بردار وقتی مساوی اند که مولفه های اول آنها با هم و مولفه های دو آن ها با هم برابر باشند.
با توجه به این تعریف لزومی ندارد که دو بردار مساوی از یک نقطه شروع شده باشند.
واضح است که می توان بیشمار بردار که مساوی هستند را در صفحه درنظر گرفت. به این بردارهای برابر، در اصطلاح، بردارهای هم ارز گفته می شود.
چگونه برای یک بردار یک عبارت جمع بنویسیم؟
با مشخص بودن مختصات ابتدا، مختصات بردار و مختصات انتهای یک بردار می توان یک جمع متناظر برای بردار نوشت. جمع مختصات ابتدای بردار با مختصات بردار برابر با مختصات انتهای بردار است.
توجه: اگر ابتدای بردار مبدا مختصات باشد مختصات بردار همان مختصات انتهای بردار است. مثلا در بردار می توان مبدا مختصات را ابتدای بردار در نظر گرفت و مختصات
را مختصات انتهای بردار در نظر بگیریم. به طور کلی:
بردارهای واحد در فضای دو بعدی چگونه اند؟
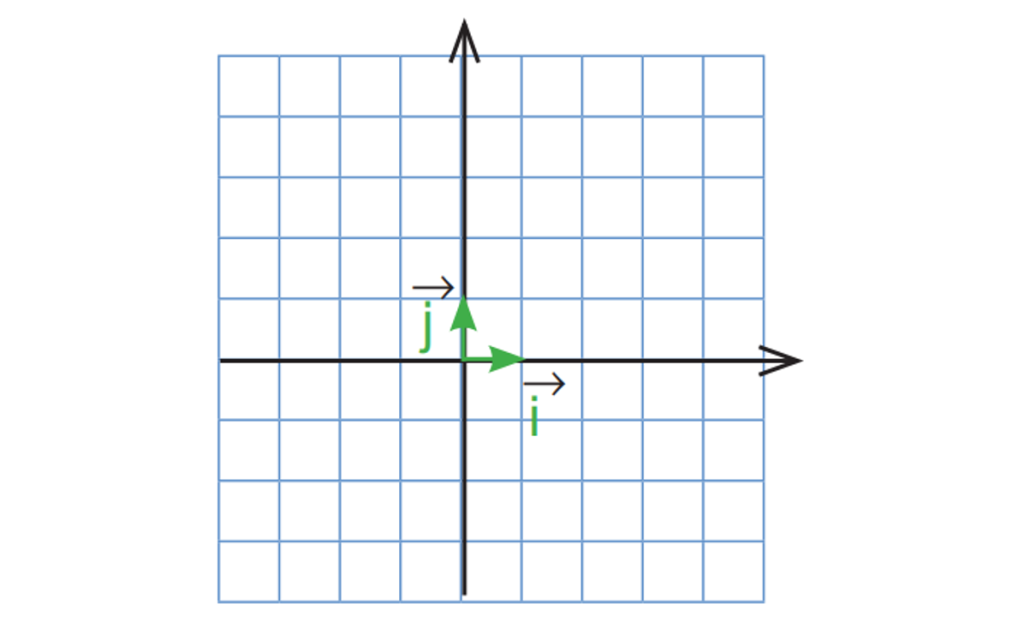
مختصات بردار را می توان بر حسب بردارهای واحد بنویسیم. بردارهای واحد مختصات در شکل زیر مشخص شدند بردار بردار واحد طول و بردار
بردار واحد عرض است.
مثلا بردار را می توان به صورت
نیز نوشت.
چطور دو بردار را جمع یا تفریق کنیم؟
برآیند یا جمع دو بردار با جمع کردن مولفه های اول شان با هم و جمع کردن مولفه های دوم شان با هم بدست می آید:
تساوی برداری را به صورت و تساوی مختصاتی را به صورت
می نویسیم. اگر بخواهیم این جمع برداری را بر حسب بردارهای واحد بنویسیم داریم:
برای تفریق دو بردار داریم:
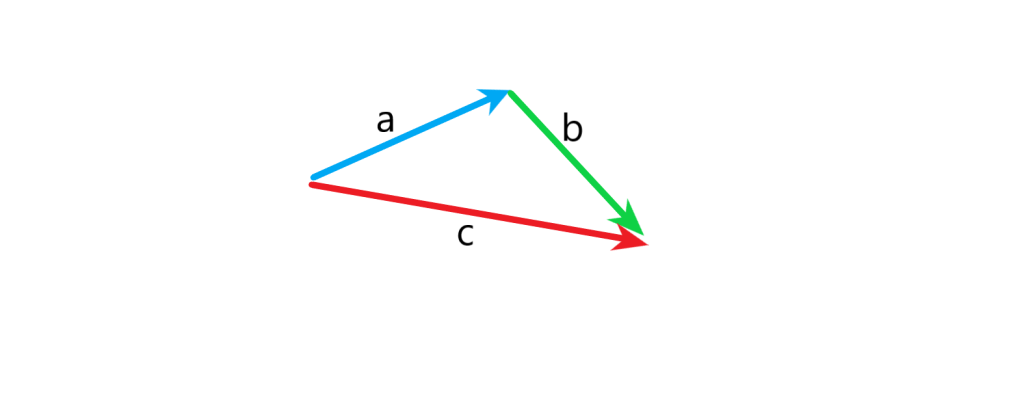
توجه: با توجه به شکل بالا اگر دو بردار و
داشته باشیم به طوری که ابتدای
در انتهای
قرار گیرد برای رسم برآیند دو بردار کافی است برداری از ابتدای بردار
به انتهای بردار
رسم کنیم.
جمع دو بردار قرینه برابر با بردار صفر است. بردار صفر را به صورت نشان می دهیم.
به طور کلی برای جمع و تفریق دو بردار می توان نوشت :
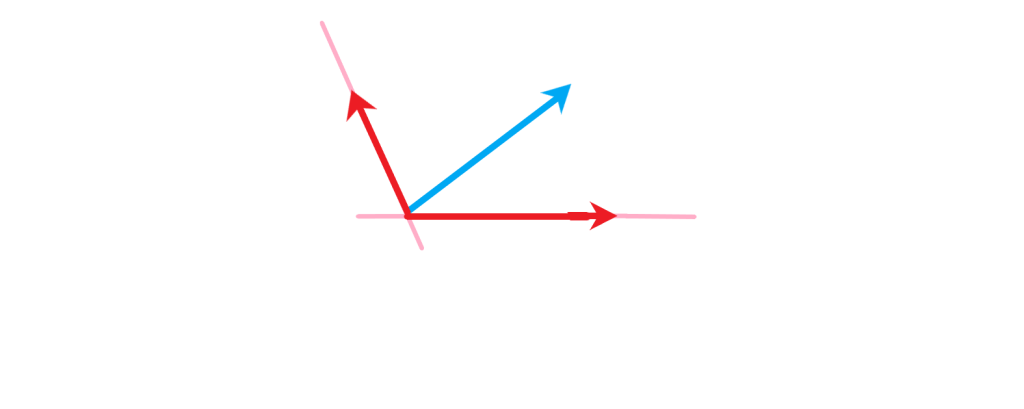
چگونه یک بردار را در دو راستا تجزیه کنیم؟
یک بردار را می توانیم به دو راستا تجزیه کنیم که به این عمل تجزیه بردار می گویند. مشخص است می توان بی شمار راستا تعیین کرد و به این ترتیب می توان گفت هر بردار را می توان به بیشمار شکل به صورت حاصل جمع دو بردار نوشت.
چگونه یک عدد را در یک بردار ضرب کنیم؟
در ضرب یک عدد در بردار، آن عدد را در طول (مولفه اول) و عرض (مولفه دوم) بردار ضرب می کنیم. به طور کلی اگر و
یک بردار باشد بردار
بصورت زیر تعریف می شود:
می توان نشان داد دو بردار و
همواره با هم موازی اند و بالعکس اگر دو بردار موازی باشند آنگاه یکی از آنها مضرب دیگری است.
قرینه یک بردار در فضای دو بعدی چگونه بدست می آید؟
اگر قرینه بردار
بدست می آید :
اگر بردار قرینه بردار
باشد می نویسیم
معرفی فضای سه بعدی
مجموعه تمام سه تایی های مرتب که در آنها
اعداد حقیقی اند را به صورت زیر در نظر گرفت که به آن فضای
می گویند.
فضای را با استفاده از یک دستگاه مختصات متشکل از سه محور دو به دو عمود بر هم که در نقطه ای مانند
متقاطع اند. این محل تقاطع مبدا دستگاه مختصات است. و مختصات
را برای آن قرارداد می کنیم.
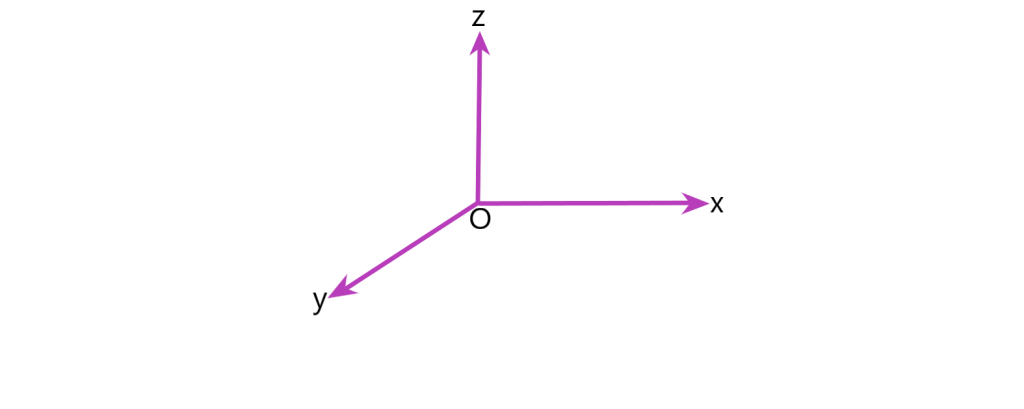
طبق شکل زیر محور محور
ها محور
محور
ها و محور
محور
ها نامیده می شوند.
با در نظر گرفتن قسمت منفی هر محور، می توان گفت محورهای مختصات، فضای سه بعدی را به هشت ناحیه تقسیم می کنند.
می توان سه نقطه به طولهای به ترتیب بر روی محورهای
در نظر گرفت و سپس صفحه گذرنده از
و موازی با صفحه
، صفحه گذرنده از
و موازی با صفحه
و صفحه گذرنده از
و موازی با صفحه
را در نظر بگیریم. محل تقاطع این سه صفحه یک نقطه به طول
، عرض
و ارتفاع
است که نمایش دهنده سه تایی مرتب
می باشد.
نکته: فقط وقتی دو نقطه منطبق اند که
و
و
باشند در اینصورت می نویسیم :
نکته: فاصله دو نقطه دلخواه در فضای: فاصله دو نقطه
و
بصورت زیر بدست می آید:
بردارها در فضای سه بعدی چگونه اند؟
مانند بردارها در فضای اگر مبدا مختصات را ابتدای همه ی بردارها در نظر بگیریم هر نقطه از فضا مانند
می تواند انتهای بردار باشد و پاره خط جهت داری که مبدا مختصات را به نقطه
وصل کند یک بردار است. این بردار را می توان با
یا
نشان داد.
اگر انتهای بردار همان مبدا مختصات باشد آن بردار بردار صفر است:
طول یک بردار در فضای سه بعدی چگونه بدست می آید؟
برای بدست آوردن طول بردار داریم :
چگونه دو بردار را در فضای سه بعدی با هم جمع و تفریق کنیم؟
برای جمع و تفریق دو بردار می توان نوشت :
چگونه یک عدد را در یک بردار در فضای سه بعدی ضرب کنیم؟
اگر و
یک بردار باشد بردار
بصورت زیر تعریف می شود:
می توان نشان داد دو بردار و
همواره با هم موازی اند و بالعکس اگر دو بردار موازی باشند آنگاه یکی از آنها مضرب دیگری است.
قرینه یک بردار در فضای سه بعدی چگونه بدست می آید؟
اگر قرینه بردار
بدست می آید:
جمع بردارها و ضرب عدد در یک بردار چه ویژگی هایی دارند؟
در جدول زیر می توانید ویژگی های جمع بردارها و ضرب عدد در بردار را ببینید:
بردارهای یکه در فضای سه بعدی چگونه اند؟
در فضای بردارهای یکه در جهت محورهای مختصات را بصورت زیر در نظر می گیریم:
و برای اینکه بردار را بر حسب بردارهای یکه بنویسیم بصورت زیر عمل می کنیم :
ضرب داخلی دو بردار چگونه انجام می شود؟
اگر و
دو بردار در فضای
باشند در اینصورت ضرب داخلی این دو بردار را که با نماد
نمایش می دهیم بصورت زیر تعریف می کنیم:
همچنین اگر زاویه بین دو بردار برابر باشد ضرب داخلی را از فرمول زیر هم می توان بدست آورد:
ضرب داخلی دو بردار چه ویژگی هایی دارد؟
ویژگی های ضرب داخلی دو بردار را می توانید در جدول زیر ببینید:
تصویر قائم یک بردار بر بردار دیگر چگونه بدست می آید؟
تصویر قائم بردار بر بردار
به صورت زیر بدست می آید:
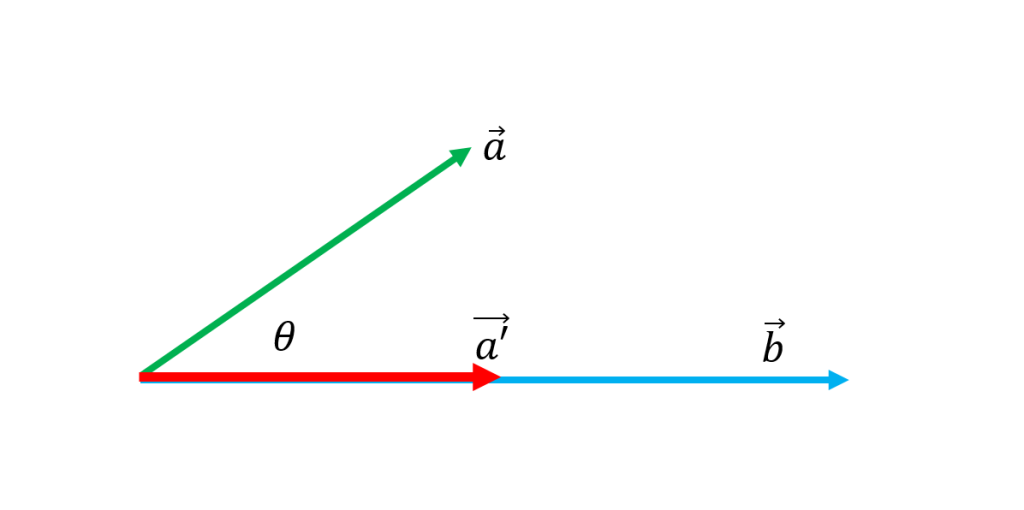
دو بردار غیرصفر و
را که زاویه بین آنها
است را با فرض اینکه
زاویه تند است در نظر می گیریم می خواهیم تصویر قائم بردار
را بر امتداد بردار
که آن را با
نمایش داده ایم بدست آوریم از روی شکل مشخص است که یک
حقیقی وجود دارد که
با توجه به اینکه تفاضل دو بردار
و
بر بردار
عمود است. داریم :
در نتیجه تصویر قائم بر امتداد بردار
به صورت زیر بدست می آید:
ضرب خارجی دو بردار چگونه انجام می شود؟
اگر و
دو بردار در فضای
باشند در اینصورت ضرب خارجی این دو بردار را که با نماد
نمایش می دهیم بصورت زیر تعریف می کنیم:
برای یادگیری نحوه بدست آوردن دترمینان ماتریس 3 در 3 می توانید به بخش ماتریس مراجه کنید.
همچنین اگر زاویه بین دو بردار برابر باشد ضرب داخلی را از فرمول زیر هم می توان بدست آورد:
جواب ضرب خارجی بردارهای یکه چیست؟
ضرب خارجی بردارهای یکه به صورت زیر انجام می شود:
ضرب خارجی دو بردار چه ویژگی هایی دارد؟
ویزگی های ضرب خارجی را می توانید در جدول زیر ببینید:
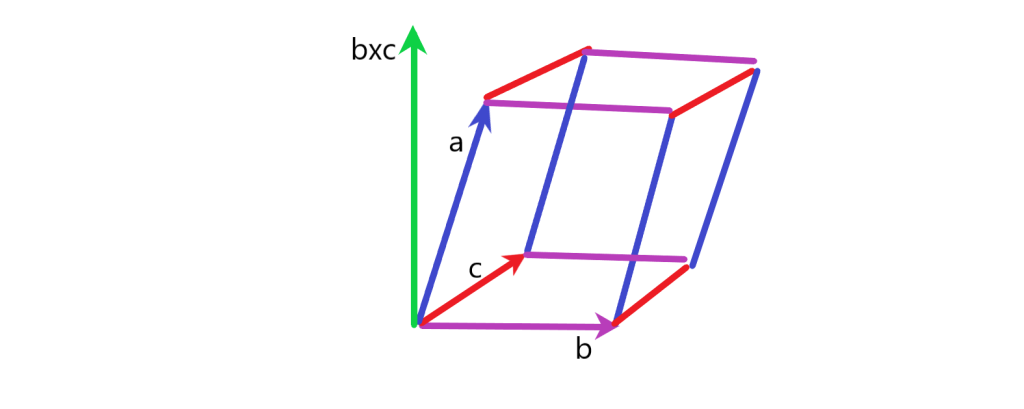
حجم متوازی السطوح چگونه بدست می آید؟
سه بردار غیر واقع بر یک صفحه باشند آنگاه به کمک آنها می توان متوازی السطوح ایجاد کرد. در شکل زیر یک متوازی السطوح که با استفاده از سه بردار ساخته شده را می بینید:
جمع بندی
در این مقاله به آموزش جامع بردارها، جمع و تفریق آنها، ضرب عدد در بردار، بردارهای مساوی و قرینه و بردار واحد پرداختیم همچنین بردارها را در فضای سه بعدی بررسی کردیم. ضرب داخلی، ضرب خارجی بردارها و تصویر قائم یک بردار بر دیگری را بیان کردیم. در آخر به آموزش بدست آوردن حجم متوازی السطوح پرداختیم. در این بین به ذکر همه ی خواص جمع بردارها ضرب داخلی بردارها و ضرب خارجی بردارها پرداختیم. در این مقاله هر آنچه که لازم است درباره بردارها بدانید بیان شده است. با خواندن این مقاله دیگر نیاز به خواندن مقاله ی دیگری درباره بردارها پیدا نمی کنید. لطفا نظرات خود را درباره مقاله بردار بیان کنید. اگر نیاز به دانستن اطلاعات بیشتری در باره ی صفحه مختصات هستید لطفا به مقاله مربوطه مراجعه فرمایید.

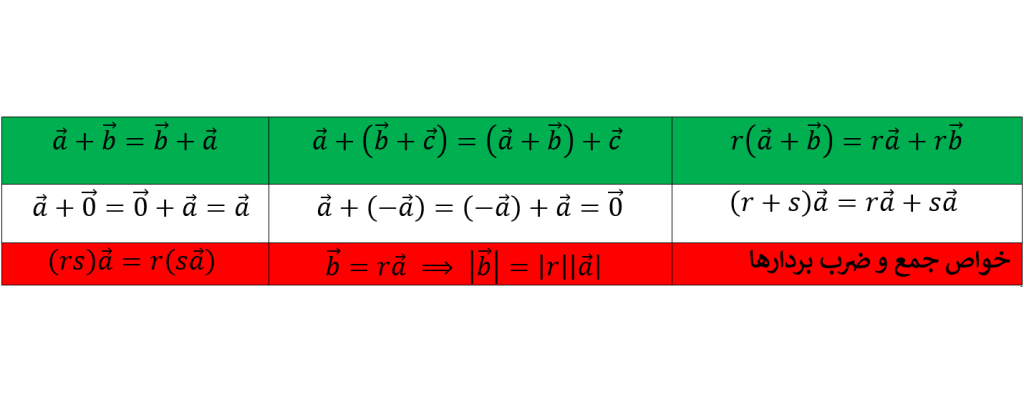

![Rendered by QuickLaTeX.com \[\rightarrow r=\frac{\overrightarrow{a}.\overrightarrow{b}}{|\overrightarrow{b}|^{2}}\]](https://faramath.com/core/ql-cache/quicklatex.com-e4c499c6e38b005ccde94f8d5ac0f6f5_l3.png)
![Rendered by QuickLaTeX.com \[\overrightarrow{a^{'}}=r\overrightarrow{b}=\frac{\overrightarrow{a}.\overrightarrow{b}}{|\overrightarrow{b}|^{2}}\overrightarrow{b}\]](https://faramath.com/core/ql-cache/quicklatex.com-717118744c9e217591f5e3349656b08b_l3.png)
![Rendered by QuickLaTeX.com \[\overrightarrow{a} \times \overrightarrow{b}=\begin{vmatrix}i &j&k \\ a_{1}& a_{2} &a_{3} \\ b_{1}& b_{2} & b_{3} \end{vmatrix}\]](https://faramath.com/core/ql-cache/quicklatex.com-77760241417c1ce51e5ea862f90cfbd8_l3.png)
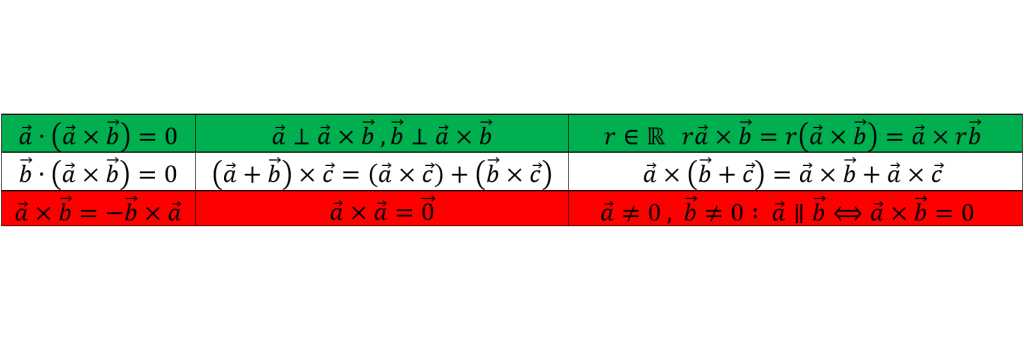
![Rendered by QuickLaTeX.com \[h=\frac{\overrightarrow{a}.(\overrightarrow{b}\times \overrightarrow{c})}{|\overrightarrow{b}\times \overrightarrow{c}|^{2}}(\overrightarrow{b}\times \overrightarrow{c})\]](https://faramath.com/core/ql-cache/quicklatex.com-f37ab5ea2d2b910a056f4aae6fc41380_l3.png)
![Rendered by QuickLaTeX.com \[|\frac{\overrightarrow{a}.(\overrightarrow{b}\times \overrightarrow{c})}{|\overrightarrow{b}\times \overrightarrow{c}|^{2}}(\overrightarrow{b}\times \overrightarrow{c})(|\overrightarrow{b}\times \overrightarrow{c}|)|\]](https://faramath.com/core/ql-cache/quicklatex.com-e426eced39df39afea5550ef64a1674a_l3.png)
![Rendered by QuickLaTeX.com \[|\overrightarrow{a}.(\overrightarrow{b} \times \overrightarrow{c})|=\begin{vmatrix} a_{1}& a_{2} &a_{3} \\ b_{1} & b_{2} &b_{3} \\ c_{1} & c_{2} & c_{3} \end{vmatrix}\]](https://faramath.com/core/ql-cache/quicklatex.com-67521cf6a9ca3972e129e55f2ea0bf6c_l3.png)
