کامل ترین آموزش در مورد بدست آوردن حجم، مساحت کل و مساحت جانبی حجم های هندسی
حجم ها از حرکت یک سطح در فضا ایجاد می شوند. حجم ها می توانند هندسی باشند یا غیرهندسی باشند. در این مقاله به بررسی حجم های هندسی و انواع آن می پردازیم. در این مقاله همچنین نحوه ی بدست آوردن حجم، مساحت جانبی و مساحت کل منشورها و نحوه بدست آوردن حجم و مساحت کره و حجم هرم توضیح داده شده است. برای اینکه از این مقاله بهره بیشتری ببرید بهتر است قبل از خواندن این مقاله به یادگیری مساحت اشکال در مقاله ی مساحت و محیط بپردازید سپس به این مقاله بازگردید.
حجم چیست؟
با حرکت یک سطح در فضا، حجم ساخته می شود. حجم ها را می توان به دو دسته هندسی و غیرهندسی تقسیم کرد. حجم های هندسی شکل های مشخص و تعریف شده دارند. حجم های هندسی را می توان به سه دسته اصلی تقسیم کرد: منشوری – کروی – هرمی . برخی از حجم های هندسی نیز ترکیبی از این سه نوع اند.
اگر سطحی را حول یک محور دوران دهیم یک حجم ساخته می شود. از این خاصیت در خراطی، تراشکاری و سفالگری برای ساختن حجم های مختلف استفاده می شود. ( اگر علاقمند به یادگیری مفهوم دوران هستید می توانید به مقاله تبدیل هندسی مراجعه کنید)
مثلا اگر دایره را حول قطرش دوران دهیم کره ایجاد می شود. اگر نیم دایره را حول قطرش دوران دهیم کره ایجاد می شود اگر ربع دایره را حول یکی از شعاع هایش دوران دهیم نیم کره ایجاد می شود در همه این موارد شعاع کره همان شعاع دایره است.
اگر مستطیل را حول طولش دوران دهیم یک استوانه به شعاع عرض مستطیل و به ارتفاع طول آن ایجاد می شود. ( اگر دوست دارید بیشتر درباره مستطیل بدانید به مقاله چهارضلعی ها مراجعه کنید)
اگر مستطیل را حول عرض ش دوران دهیم یک استوانه به شعاع طول مستطیل و به ارتفاع عرض آن ایجاد می شود.
اگر یک مثلث قائم الزاویه را حول یک ضلع قائمه دوران دهیم یک مخروط در فضای سه بعدی ایجاد می شود.
در ادامه به بررسی سه دسته اصلی حجم های هندسی می پردازیم.
منشور ( انواع منشور ، مساحت و حجم آنها )
منشور دارای دو وجه مساوی و موازی هست که به آن دو قاعده منشور می گویند این دو وجه با یکسری پاره خط به هم متصل می شوند و وجه هایی را در اطراف بوجود می آورند به وجه های اطراف وجه های جانبی می گویند. به محل برخورد هر دو سطح یال و به نقطه برخورد هر سه سطح راس می گویند.
اگر این دو سطح 
ضلعی باشند منشور حاصل 
راس دارد. 
یال دارد. وجه جانبی دارد. 
وجه دارد.
خط عمود بین دو قاعده را ارتفاع منشور می گویند.
تمام سطوح جانبی منشور فارغ از اینکه شکل سطح قاعده چیست، متوازی الاضلاع است.
حجم منشور برابر است با حاصلضرب مساحت قاعده در ارتفاع آن :
![\[V=Ah\]](https://faramath.com/core/ql-cache/quicklatex.com-37faa0dce6ee004c75cc1eb6be25b826_l3.png "Rendered by QuickLaTeX.com")
مساحت جانبی منشور برابر است با حاصل ضرب محیط قاعده در ارتفاع
![\[S^{'}=Ph\]](https://faramath.com/core/ql-cache/quicklatex.com-ff90ed845605b2c32e12aad0c080c511_l3.png "Rendered by QuickLaTeX.com")
مساحت کل منشور برابر است با مجموع مساحت قاعده ها و مساحت جانبی
![\[S=2A+Ph\]](https://faramath.com/core/ql-cache/quicklatex.com-8e4390ad5dea0b862417ddf69f25200d_l3.png "Rendered by QuickLaTeX.com")
توجه: اگر برای بدست آوردن حجم و مساحت جانبی به دانستن مساحت و محیط نیاز دارید حتما به مقاله مربوطه مراجعه فرمایید.
چند منشور معروف:
مکعب مستطیل: اگر سطوح قاعده مربع یا مستطیل شکل باشد به منشور حاصل مکعب مستطیل نیز می گویند. حجم مکعب مستطیل را می توان به صورت حاصلضرب طول و عرض و ارتفاع نیز بدست آورد.
استوانه: اگر سطوح قاعده دایره باشد به منشور حاصل استوانه نیز می گویند.
با لوله کردن یک مستطیل می توان استوانه ساخت. در حالتی که عرض مستطیل ارتفاع باشد حجم استوانه بیشتر است.
مکعب: اگر هم سطوح قاعده و هم سطوح جانبی مربع شکل باشد به منشور حاصل مکعب یا مکعب مربع نیز می گویند.
حجم مکعب برابر است با اندازه ضلع مربع به توان سه.
هرم ( انواع هرم و حجم آنها )
هرم شامل یک سطح است که که راس هایش را به یک نقطه که شامل صفحه ی سطح قاعده نیست وصل شده است. این سطح می تواند هر شکلی باشد. اگر این سطح دایره باشد به هرم تشکیل شده مخروط هم می گویند.
اگر دو هرم دارای قاعده های هم مساحت و ارتفاع های مساوی باشند، حجم های آنها با هم برابر است.
حجم هر هرم با مساحت قاعده 
و ارتفاع 
برابر است با
![\[V=\frac{1}{3}Sh\]](https://faramath.com/core/ql-cache/quicklatex.com-3dda350f78686b0a9f0929f3b6593d0b_l3.png "Rendered by QuickLaTeX.com")
مخروط، شکلی شبیه هرم منتظم است که قاعده آن به شکل دایره و پای ارتفاع مخروط مرکز این دایره است.
کره ( مساحت و حجم آن)
کره مجموعه نقاطی از فضا است که همه ی آن نقطه ها از یک نقطه در همان فضا به نام مرکز به یک فاصله ثابت و مشخص هستند. به این اندازه ثابت، شعاع کره می گوییم.
حجم کره به شعاع R از دستور 
بدست می آید.
مساحت کره به شعاع 
از دستور 
بدست می آید.
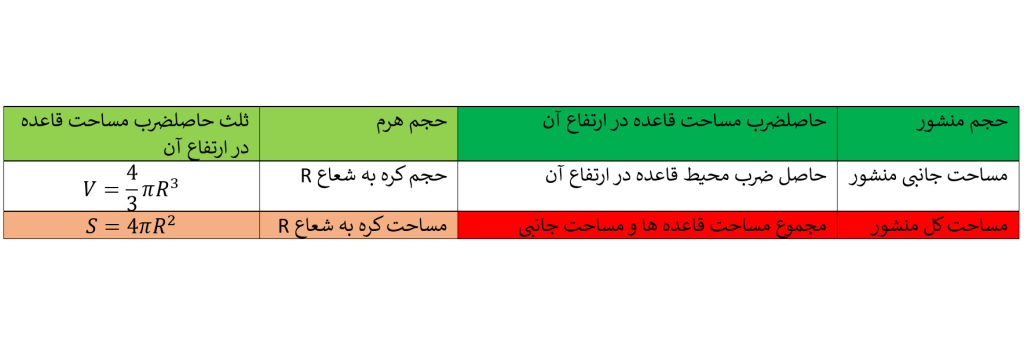
در جدول زیر خلاصه ی از فرمول های مربوط به حجم می بینید:
برش حجم های هندسی
تعریف: شکلی که از برخورد یک صفحه با یک جسم هندسی حاصل می شود، سطح مقطع آن نامیده می شود.
اگر مخروط قائم را با صفحه ای موازی با قاعده برخورد دهیم، مخروط به دو شکل تقسیم می شود قسمت بالایی یک مخروط کوچکتر است و قسمت پایینی یک مخروط ناقص است.
وقتی یک حجم را برش بزنیم می گوییم عمل مقطع زدن را انجام دادیم.
وقتی یک سطح مخروطی توسط یک صفحه برش داده می شود، معمولا سطح مقطع یک منحنی است. از آنجا که این منحنی ها حاصل تقاطع یک صفحه با یک سطح مخروطی هستند، مقاطع مخروطی نامیده می شوند. اگر علاقمند به کسب اطلاعات بیشتر در مورد مقاطع مخروطی هستید لطفا به مقاله مربوطه مراجعه کنید.
جمع بندی
در این مقاله به آموزش انواع حجم هندسی و غیرهندسی پرداخته ایم. شکل، فرمولِ حجم و مساحت این حجم های هندسی را بیان کردیم. اگر به خواندن مقاله محیط و مساحت نیاز دارید یا در مورد مقاطع مخروطی کنجکاو هستید به مقالات مربوطه مراجعه کنید. لطفا در قسمت کامنت ها ما را از نظرات خود درباره مقاله حجم بهره مند کنید.
