کامل ترین آموزش درباره اعداد اول
اعداد اول در زبان انگلیسی 
نام دارند. اعداد اول زیرمجموعه ای از اعداد طبیعی و در نتیجه زیرمجموعه اعداد حقیقی هستند. در این مقاله به آموزش شمارنده ها می پردازیم از قوانین بخش پذیری اعداد صحبت می کنیم. با تجزیه اعداد به عوامل اول آشنا شده و کاربرد آن در ساده کردن کسرها یا همان اعداد گویا ، بدست آوردن بزرگترین شمارنده مشترک و کوچکترین مضرب مشترک بررسی می کنیم. در ادامه به نحوه تشخیص اعداد اول و روش غربال می پردازیم. در این آموزش با ما همراه باشید.
چطور شمارنده های یک عدد را بدست آوریم؟
اگر 12 تا مهره داشته باشید چطور می توانید آن ها را دسته بندی کنید تا تعداد مهره های هر دسته با هم برابر باشند؟ حتما جواب می دهید معلوم است دیگر 12 دسته یکی یا 6 دسته دوتایی یا 4 دسته سه تایی یا 3 دسته چهارتایی یا 2 دسته شش تایی یا 1 دسته دوازده تایی.
در واقع اگر جدول ضرب را حفظ باشید به راحتی می توانید به این سبک سوالات جواب دهید.
اگر بخواهیم شمارنده های یک عدد را بدست آوریم کافی است به این فکر کنیم که آن عدد بر چه اعدادی قابل تقسیم است. مثلا 12 بر 1 و 2 و 3 و 4 و 6 و 12 بخش پذیر است. پس اعداد
شمارنده های 12 هستند.
سوال: شمارنده های اعداد 15 و 36 و 24 و 18 و 17 را بدست آورید.
جواب: برای هر کدام از اعداد به این فکر کنید که با آن تعداد مهره چند دسته می توان ساخت که تعداد مهره های هر دسته با هم برابر باشند.
![\[15:\{1,3,5,15\}\]](https://faramath.com/core/ql-cache/quicklatex.com-3371b6d7907e6c79345a5b4b50b27aba_l3.png "Rendered by QuickLaTeX.com")
![\[36:\{1,2,3,4,6,9,12,18,36\}\]](https://faramath.com/core/ql-cache/quicklatex.com-ef2372559308989754b323b093849671_l3.png "Rendered by QuickLaTeX.com")
![\[24:\{1,2,3,4,6,8,12,24\}\]](https://faramath.com/core/ql-cache/quicklatex.com-7942af6982fbe1fe8f9855690e730bfc_l3.png "Rendered by QuickLaTeX.com")
![\[18:\{1,2,3, 6,9,18\}\]](https://faramath.com/core/ql-cache/quicklatex.com-9ea6d1266e453896c039020a6eb60823_l3.png "Rendered by QuickLaTeX.com")
![\[17:\{1,17\}\]](https://faramath.com/core/ql-cache/quicklatex.com-ce7a1b6f5d477ea5ec6422b4e2a1e603_l3.png "Rendered by QuickLaTeX.com")
توجه: به شمارنده های یک عدد مقسوم علیه های آن عدد هم می گویند. در واقع هر عدد به شمارنده هایش قابل تقسیم است.
نکاتی در مورد شمارنده ها
- عدد 1 شمارنده همه ی اعداد است.
- کوچکترین شمارنده هر عدد 1 است.
- بزرگترین شمارنده هر عدد خود عدد است.
- همه ی شمارنده های یک عدد کوچکتر مساوی آن عدد هستند.
- هر عدد بزرگتر از 1 حداقل دو شمارنده دارد.
- عدد1 فقط یک شمارنده دارد که خودش است.
- بعضی اعداد فقط دو شمارنده دارند.
اعداد اول چیستند؟
به اعدادی مثل 
که هر کدام فقط دو شمارنده دارند که یکی از آنها 1 و دیگری خودشان است، اعداد اول می گویند. به بیان دیگر اعداد اول را نمی توان به صورت حاصلضرب دو عدد بزرگتر از یک نوشت.
اعداد طبیعی غیر از 1 که اول نیستند اعداد مرکب نام دارند. در واقع اعداد طبیعی را می توان به سه دسته افراز کرد: عدد یک، اعداد اول، اعداد مرکب.
چطور یک عدد طبیعی را به اعداد اول تجزیه کنیم؟
همه ی اعداد مرکب را می توان به صورت حاصلضرب اعداد اول نوشت. برای مثال می توان عدد 30 را به صورت زیر تجزیه کرد (تجزیه کردن یک عدد یعنی آن عدد را به صورت حاصلضرب اعداد دیگر بنویسید.)
![\[30=2\times15=2\times3\times5\]](https://faramath.com/core/ql-cache/quicklatex.com-55235f567a8b6e21d6ffa9ea7e8cf874_l3.png "Rendered by QuickLaTeX.com")
اینجا می بینیم که ابتدا 30 به صورت حاصل ضرب 2 و 15 نوشته شده عدد 2 را نمی توان به صورت حاصلضرب دو عدد بزرگتر از یک نوشت و عددی اول است اما 15 را می توان به صورت 
نوشت. که 3 و 5 هم اعداد اول هستند پس توانستیم عدد 30 را بصورت حاصلضرب اعداد اول بنویسیم.
مثال: عددهای 36 و 100 و 210 و 6 و 8 را به صورت حاصلضرب شمارنده های اول آن بنویسید.
جواب:
![\[8=2\times4=2\times2\times2\]](https://faramath.com/core/ql-cache/quicklatex.com-f0de5d02f84a6c7ee43b2dddd35757ef_l3.png "Rendered by QuickLaTeX.com")
![\[6=2\times3\]](https://faramath.com/core/ql-cache/quicklatex.com-c32c88f2f25f96f7d0d9410f112d313e_l3.png "Rendered by QuickLaTeX.com")
![\[210=21\times10=3\times7\times2\times5\]](https://faramath.com/core/ql-cache/quicklatex.com-66ac24e4961ba54ce39efce541376663_l3.png "Rendered by QuickLaTeX.com")
![\[100=10\times10=2\times5\times2\times5\]](https://faramath.com/core/ql-cache/quicklatex.com-ccf6f4a4b40d3c53a0e9cefbb61e5539_l3.png "Rendered by QuickLaTeX.com")
![\[36=6\times6=2\times3\times2\times3\]](https://faramath.com/core/ql-cache/quicklatex.com-7ee8dd586c51dba1d3c68f2e520bc07f_l3.png "Rendered by QuickLaTeX.com")
سوال: عددی بعد از تجزیه به صورت 
درآمده شمارنده های اول این عدد چه اعدادی هستند؟
جواب: مطابق تجزیه زیر اعداد 2 و 3 و 5 و 7 شمارنده های اول این عدد هستند.
![\[4\times25\times12\times42=\]](https://faramath.com/core/ql-cache/quicklatex.com-3dd4ca01e5893dc5ec484cb91997eb53_l3.png "Rendered by QuickLaTeX.com")
![\[(2\times2)\times(5\times5)\times(3\times2\times2) )\times(2\times3\times7)\]](https://faramath.com/core/ql-cache/quicklatex.com-639411d54508ed7e2b373ea5e2d0ff2a_l3.png "Rendered by QuickLaTeX.com")
نکاتی در مورد اعداد اول
- تنها عدد زوج که اول است عدد 2 است.
- همه ی اعداد اول غیر از 2 فرد هستند.
- اگر حاصل جمع دو عدد اول عددی فرد شد حتما یکی از آن دو عدد، عدد 2 است. (برای متوجه شدن دلیل آن به مقاله ی اعداد طبیعی مراجعه کنید)
- برای اعداد اول هنوز فرمولی کشف نشده است.
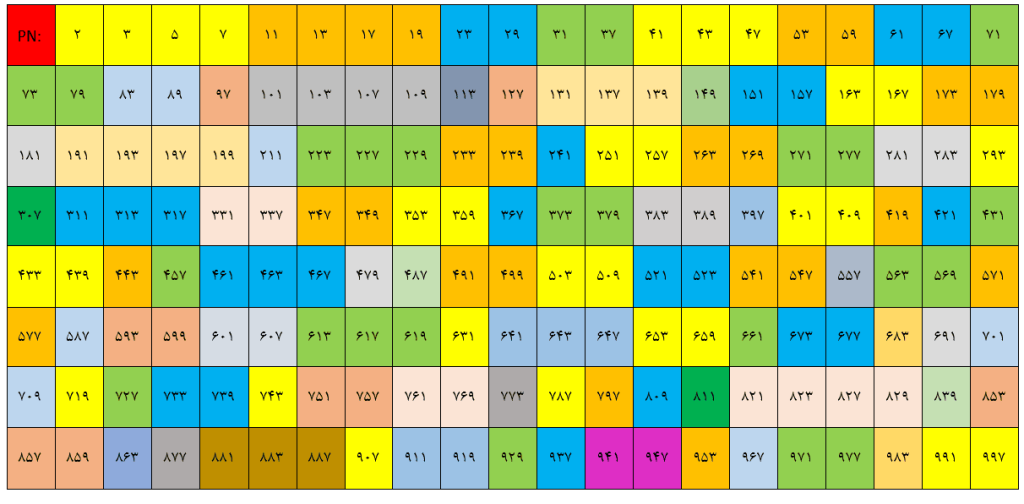
- به جدول اعداد زیر که اعداد اول 1 تا 1000 را نشان می دهد توجه کنید. در این جدول می توانید لیست اعداد اول 1 تا 1000 را مشاهده کنید.
کاربرد اعداد اول در ساده کردن کسرها
با دانستن اعداد اول و نحوه تجزیه اعداد مرکب به اعداد اول، می توان کسرها را راحت تر ساده کرد. یادگیری این موضوع، به شما در حل مسائل فیزیک، شیمی و همچنین سایر مباحث ریاضی یاری می کند.
برای ساده کردن یک کسر کافی است صورت و مخرج کسر را به صورت حاصل ضرب شمارنده های اولشان نوشت و سپس شمارنده های یکسان در صورت و مخرج را حذف کرد. برای مثال برای ساده کردن کسر 
باید ابتدا 48 و 30 را به عوامل اولش تجزیه کرد:
![\[48=6\times8=2\times3\times2\times2\times2\]](https://faramath.com/core/ql-cache/quicklatex.com-231b82883bf05ddee4a25a8e8753403d_l3.png "Rendered by QuickLaTeX.com")
![\[30=5\times6=5\times2\times3\]](https://faramath.com/core/ql-cache/quicklatex.com-e128b1d1563d5f1d9b1aef84413728fe_l3.png "Rendered by QuickLaTeX.com")
حالا کسر را بصورت زیر می نویسیم:
![\[\frac{48}{30}=\frac{2\times3\times2\times2\times2}{5\times2\times3}=\]](https://faramath.com/core/ql-cache/quicklatex.com-0db3cd4c1b33182785c32f5ad85d6eb8_l3.png "Rendered by QuickLaTeX.com")
![\[\frac{2\times3}{2\times3}\times\frac{2\times2\times2}{5}=\frac{8}{5}\]](https://faramath.com/core/ql-cache/quicklatex.com-1f59e110fe36396ac67a09199e354487_l3.png "Rendered by QuickLaTeX.com")
بنابراین کسر ساده شده ی برابر 
است.
چطور بزرگترین شمارنده مشترک دو عدد را بدست آوریم؟
وقتی شمارنده های دو عدد 
و 
را بدست آوریم بزرگترین شمارنده ی مشترک بین شمارنده های دو عدد را با 
نشان می دهیم.
مثال: می خواهیم 
را بدست آوریم می دانیم شمارنده های 15 برابر 
و شمارنده های 24 برابر 
هستند. شمارنده های مشترک آنها برابر 
که بین این اعداد 3 بزرگتر است. بنابراین
![\[(15,24)=3\]](https://faramath.com/core/ql-cache/quicklatex.com-d24ac92849e7183b7842229ea2ba134c_l3.png "Rendered by QuickLaTeX.com")
یک راه دیگر برای بدست آوردن بزرگترین شمارنده مشترک بین دو عدد این است که هر عدد را به صورت حاصلضرب عوامل اول ش بنویسیم و بعد حاصلضربِ کمترین تعداد در عوامل مشترک را به عنوان بزرگترین شمارنده مشترک در نظر می گیریم.
مثال: می خواهیم را بدست آوریم می دانیم
![\[24=2\times2\times2\times3\]](https://faramath.com/core/ql-cache/quicklatex.com-f4a5fe807139eb205696ece82c340b77_l3.png "Rendered by QuickLaTeX.com")
![\[15=3\times5\]](https://faramath.com/core/ql-cache/quicklatex.com-070a7304c2bd948632c0b8101158635f_l3.png "Rendered by QuickLaTeX.com")
تنها عامل مشترک بین این ها 3 است پس
مثال: می خواهیم 
را بدست آوریم می دانیم
![\[36=3\times3\times 2\times 2\]](https://faramath.com/core/ql-cache/quicklatex.com-e53a9d5fd51e9aaacc116ff6b0aa00e3_l3.png "Rendered by QuickLaTeX.com")
عدد 24 سه تا 2 و یکی 3 دارد و عدد 36 دو تا 2 و دو تا 3 دارد پس کمترین تعداد 2 برابر دو و کمترین تعداد 3 برابر یک است پس داریم:
![\[(36,24)=3\times2\times2=12\]](https://faramath.com/core/ql-cache/quicklatex.com-fecb52bd7cbc185267163534111357eb_l3.png "Rendered by QuickLaTeX.com")
نکاتی در مورد بزرگترین شمارنده مشترک
- اگر دو عدد اول باشند بزرگترین شمارنده مشترک آنها عدد یک می شود.
![\[(7,11)=1\,\,\,,\,\,\,(5,23)=1\]](https://faramath.com/core/ql-cache/quicklatex.com-a8257f9bd6b4c9caab655bcc743c367e_l3.png "Rendered by QuickLaTeX.com")
![\[(2,13)=1\,\,\,,\,\,\,(29,3)=1\]](https://faramath.com/core/ql-cache/quicklatex.com-d886300fd9909e1445f97a48111c5910_l3.png "Rendered by QuickLaTeX.com")
- اگر عددی بر دیگری بخش پذیر باشد بزرگترین شمارنده مشترک آنها عدد کوچکتر می شود.
![\[(20,5)=5\,\,\,,\,\,\,(45,9)=9\]](https://faramath.com/core/ql-cache/quicklatex.com-ad431a7d9eef4e42f78b15d8cb284546_l3.png "Rendered by QuickLaTeX.com")
![\[(48,8)=8\,\,\,,\,\,\,(6,30)=6\]](https://faramath.com/core/ql-cache/quicklatex.com-a869492347cd021990b442ed6332f30a_l3.png "Rendered by QuickLaTeX.com")
- کوچکترین شمارنده مشترک دو عدد برابر یک است.
- بزرگترین شمارنده هر عدد و خودش ، برابر خود عدد می شود.
![\[(7,7)=7\,\,\,,\,\,\,(12,12)=12\]](https://faramath.com/core/ql-cache/quicklatex.com-2e16e0cacbdcd3ac1377c658e3a34125_l3.png "Rendered by QuickLaTeX.com")
![\[(35,35)=35\,\,\,,\,\,\,(37,37)=37\]](https://faramath.com/core/ql-cache/quicklatex.com-584733e878df23c98437465d0d72e05e_l3.png "Rendered by QuickLaTeX.com")
شمارنده هر دو عدد
و 
هست.
- بزرگترین شمارنده مشترک یک عدد اول با هر عدد دیگری یا یک می شود یا آن عدد اول.
![\[(20,5)=5\,\,\,,\,\,\,(5,9)=1\]](https://faramath.com/core/ql-cache/quicklatex.com-b53ddbcf462e7a4e304d43644e4c4c8d_l3.png "Rendered by QuickLaTeX.com")
![\[(32,7)=1\,\,\,,\,\,\,(32,2)=2\]](https://faramath.com/core/ql-cache/quicklatex.com-0abaaed94962847fb3ce94b56c83bc59_l3.png "Rendered by QuickLaTeX.com")
- اگر بزرگترین شمارنده مشترک دو عدد یک باشد آن دو عدد نسبت به هم اول اند. مثلا 4 و 9 نسبت به هم اول اند چون .
چطور کوچکترین مضرب مشترک دو عدد را بدست آوریم؟
هر عدد بی شمار مضرب دارد مضرب یا مضرب طبیعی به حاصل ضرب اعداد طبیعی در آن عدد گویند. مثلا مضرب های عدد 9 برابر مقادیر زیر هستند:
![\[\{9\times1=9,\,9\times2=18,\,9\times3=27,…\}\]](https://faramath.com/core/ql-cache/quicklatex.com-ba2216cd3acbc8ec73d482547064df80_l3.png "Rendered by QuickLaTeX.com")
![\[=\{9,18,27,36,…\}\]](https://faramath.com/core/ql-cache/quicklatex.com-828b83002f3cfccb8cc388c8baa704be_l3.png "Rendered by QuickLaTeX.com")
کوچکترین مضرب مشترک بین و را با ![[a,b]](https://faramath.com/core/ql-cache/quicklatex.com-fcda5ef4ae327e1afef79dc73df91703_l3.png "Rendered by QuickLaTeX.com")
نشان می دهیم. برای بدست آوردن کوچکترین مضرب مشترک بین دو عدد کافی است همه ی مضارب آن دو عدد را بنویسیم و سپس کوچکترین آنها را بدست آوریم. اما یک راه بهتر برای بدست آوردن کوچکترین مضرب مشترک بین دو عدد این است که هر عدد را به صورت حاصل ضرب اعداد اول بنویسیم. سپس حاصل ضرب عوامل غیر مشترک در بیشترین تکرار عوامل مشترک را بدست می آوریم تا کوچکترین مضرب مشترک را بدست آورده باشیم.
مثال: می خواهیم ![[15,24]](https://faramath.com/core/ql-cache/quicklatex.com-1c3023e06c60671fc730c2eb113874d1_l3.png "Rendered by QuickLaTeX.com")
را بدست آوریم می دانیم
تنها عامل مشترک بین این ها 
است و عوامل غیرمشترک 
و 
هستند. بنابراین می نویسیم
![\[[15,24]=2\times2\times2\times5\times3=120\]](https://faramath.com/core/ql-cache/quicklatex.com-590ee275410e36cff1f4536e8492e5a6_l3.png "Rendered by QuickLaTeX.com")
نکاتی در مورد کوچکترین مضرب مشترک
- اگر عددی بر دیگری بخش پذیر باشد عدد بزرگتر کوچکترین مضرب مشترک دو عدد است.
![\[[20,5]=20\,\,\,,\,\,\,[9,45]=45\]](https://faramath.com/core/ql-cache/quicklatex.com-bd36fb2a76b7412515d73d9abf8584e3_l3.png "Rendered by QuickLaTeX.com")
![\[[48,8]=48\,\,\,,\,\,\,[30,6]=30\]](https://faramath.com/core/ql-cache/quicklatex.com-b89a44284a0823c4525ad6d5dd2aa706_l3.png "Rendered by QuickLaTeX.com")
- اگر بزرگترین شمارنده مشترک دو عدد یک باشد کوچکترین مضرب مشترک دو عدد برابر حاصل ضرب دو عدد است.
![\[(a,b)=1\,\,\,\Rightarrow\,\,\,[a,b]=a\times b\]](https://faramath.com/core/ql-cache/quicklatex.com-ef825ab89871f0e683b035e7d0029f43_l3.png "Rendered by QuickLaTeX.com")
- کوچکترین مضرب مشترک دو عدد اول برابر حاصل ضرب آنها است.
![\[[7,5]=35\,\,\,,\,\,\,[11,2]=22\]](https://faramath.com/core/ql-cache/quicklatex.com-578cd40b98060536adc5717594ec6114_l3.png "Rendered by QuickLaTeX.com")
![\[[13,3]=39\,\,\,,\,\,\,[29,17]=493\]](https://faramath.com/core/ql-cache/quicklatex.com-55c0902986688c0080b8f9f1f2b733af_l3.png "Rendered by QuickLaTeX.com")
- کوچکترین مضرب مشترک هر عدد با خودش، خود عدد است.
![[a,a]=a](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%2067%2018'%3E%3C/svg%3E "Rendered by QuickLaTeX.com")
![[a,a]=a](https://faramath.com/core/ql-cache/quicklatex.com-23cee99bba3f476dd29330bb36e8d632_l3.png "Rendered by QuickLaTeX.com")
![\[[20,20]=20\,\,\,,\,\,\,[45,45]=45\]](https://faramath.com/core/ql-cache/quicklatex.com-a4215806138960c3a83f2b24c9b05731_l3.png "Rendered by QuickLaTeX.com")
![\[[8,8]= 8\,\,\,,\,\,\,[30,30]=30\]](https://faramath.com/core/ql-cache/quicklatex.com-972874ffd9109c28cbf1eee0093d26cb_l3.png "Rendered by QuickLaTeX.com")
- کوچکترین مضرب مشترک هر عدد و یک برابر آن عدد است.
![[a,1]=a](https://faramath.com/core/ql-cache/quicklatex.com-7d112127286e9f3a6bb03908fe6bf398_l3.png "Rendered by QuickLaTeX.com")
![\[[20,1]=20\,\,\,,\,\,\,[1,9]=9\]](https://faramath.com/core/ql-cache/quicklatex.com-dc62cbde1b1dc24c8c941ffb6e294194_l3.png "Rendered by QuickLaTeX.com")
![\[[4,1]= 4\,\,\,,\,\,\,[30,1]=30\]](https://faramath.com/core/ql-cache/quicklatex.com-818a1ad24c8e57f1da7d45a7b126a40d_l3.png "Rendered by QuickLaTeX.com")
- بزرگترین مضرب مشترک دو عدد نامعلوم است.
- بزرگترین مضرب یک عدد نامعلوم است.
- شمارنده
![[a,b]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%2031%2018'%3E%3C/svg%3E "Rendered by QuickLaTeX.com")
است.
- همواره
![[a,b]\times(a,b)=a\timesb](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%20126%2019'%3E%3C/svg%3E "Rendered by QuickLaTeX.com")
![[a,b]\times(a,b)=a\timesb](https://faramath.com/core/ql-cache/quicklatex.com-eb33bc56d0e17b61e8584f141ae78dc0_l3.png "Rendered by QuickLaTeX.com")
مثلا
![\[a=10\,\,\,,\,\,\,b=4\]](https://faramath.com/core/ql-cache/quicklatex.com-97322ace21d2782b743d0bee9391315d_l3.png "Rendered by QuickLaTeX.com")
![\[\rightarrow\,\,\,(10,4)=2\,\,\,,\,\,\,[10,4]=20\]](https://faramath.com/core/ql-cache/quicklatex.com-8531bc530d868dc6aa1211de1d105e13_l3.png "Rendered by QuickLaTeX.com")
![\[\Rightarrow\,\,\,(10,4)\times[10,4]=4\times10\]](https://faramath.com/core/ql-cache/quicklatex.com-afaca7c0d2c4f7ea05082fa1e13bf23f_l3.png "Rendered by QuickLaTeX.com")
![\[\rightarrow\,\,\,2\times20=4\times10=40\]](https://faramath.com/core/ql-cache/quicklatex.com-3960cd007c872218ca62814b5cc55645_l3.png "Rendered by QuickLaTeX.com")
چطور بفهمیم یک عدد اول است یا نه ؟ (نحوه تشخیص عدد اول)
برای اینکه بفهمیم که یک عدد، اول است یا نه باید آن عدد را بر اعداد اولِ کمتر از جذر ِ آن عدد تقسیم کنیم. برای مثال برای اینکه بفهمیم 23 اول است یا نه باید 23 را بر 3 و 2 تقسیم کنیم. می دانیم عدد ِ اول بعدی 5 است اما چون 
بنابراین نیاز نیست که 23 را بر 5 تقسیم کنیم. از آنجا که 23 بر 2 و 3 بخش پذیر نیست پس 23 عددی اول است.
مثال : 45 اول است یا خیر؟ برای این کار باید 45 را بر 2 و 3 و 5 تقسیم کنیم عدد اول بعدی 7 است اما چون 
پس کافی است 45 را بر این سه عدد تقسیم کنیم اگر 45 بر هیچ کدام از این سه عدد بخش پذیر نباشد عددی اول است اما اگر حداقل بر یکی از این سه عدد بخش پذیر باشد آنگاه 45 عددی مرکب است. با تقسیم 45 بر 2 متوجه می شویم که بر 2 بخش پذیر نیست اما اگر 45 را بر 3 تقسیم کنیم باقی مانده صفر می شود و 45 بر 3 بخش پذیر است پس 45 عددی مرکب است و نیاز نیست تقسیم کردن ها را ادامه دهیم.
مثال: 17 اول است یا خیر ؟ برای فهمیدن اینکه 17 اول است یا خیر باید 17 را بر 2 و 3 تقسیم کنیم عدد اول بعدی 5 است اما چون 
پس نیاز نیست 17 را بر 5 تقسیم کنیم. حالا با تقسیم 17 بر 2 و3 می بینیم بر هیچ کدام بخش پذیر نیست پس 17 عددی اول است.
قوانین بخش پذیری بر اعداد 2 و 3 و 5
برای بخش پذیری بر بعضی از اعداد قوانینی وجود دارد. با کمک این قوانین می توانیم زودتر متوجه اول یا مرکب بودن یک عدد شویم چون بدون نیاز به تقسیم کردن و فقط با استفاده از این قوانین بخش پذیری های لازم برای عدد مورد نظر را بررسی کنیم.
بخش پذیری بر 2: اگر یکان یک عدد زوج (0 یا 2 یا 4 یا 6 یا 8 ) باشد آن عدد بر 2 بخش پذیر است. اگر یکان زوج نباشد آن عدد بر 2 بخش پذیر نیست.
بخش پذیری بر 3 : برای بررسی بخش پذیری بر 3 کافی است مجموع ارقام آن عدد را حساب کنیم و اگر مجموع ارقام بر 3 بخش پذیر باشد آن عدد را بر 3 بخش پذیر است در غیر اینصورت آن عدد بر 3 بخش پذیر نیست. مثلا برای بررسی بخش پذیری 124 بر 3 باید مجموع ارقام آن را بررسی کنیم 
که 7 بر 3 بخش پذیر نیست پس 124 بر 3 بخش پذیر نیست.
بخش پذیری بر 5: برای بررسی بخش پذیری بر 5 کافی است یکان عدد را بررسی کنیم اگر یکان صفر یا 5 باشد عدد بر 5 بخش پذیر است در غیر اینصورت بر 5 بخش پذیر نیست.
برای سایر اعداد اول پیشنهاد می کنیم که تقسیم را انجام دهید چون قوانین پیچیده تر از انجام تقسیم است.
چطور در یک مجموعه اعداد، اعداد اول را پیدا کنیم؟ (روش غربال)
اگر بگویند که چند عدد اول بین اعداد 1 تا 
وجود دارد از قانون غربال استفاده می کنیم. قانون غربال می گوید که همه ی اعداد را بنویسید عدد 1 را خط بزنید و مضارب کوچکترین عدد اول یعنی 2 بجز خودش را خط بزنید بعد مضارب عدد اول بعدی یعنی 3 بجز خودش را خط بزنید اینکار را با همه ی اعداد اولی که مجذورشان کمتر مساوی از است ادامه دهید. البته خود اعداد اول را خط نزنید فقط مضارب دیگر آن را خط بزنید. با اینکار هر چه خط نخورده باقی می ماند عدد اول است.
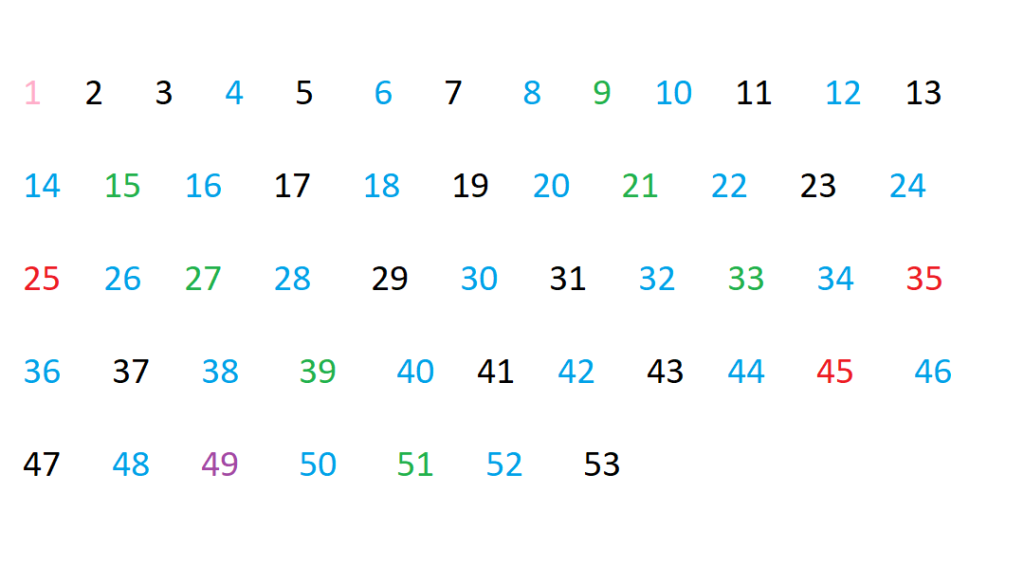
مثال: چند عدد اول بین اعداد 1 تا 53 وجود دارد؟
جواب: فرض کنید که همه ی اعداد را نوشتید و 1 را خط زدید حالا تمام مضارب عدد 2 را خط بزنید یعنی در اینجا همه ی اعداد زوج غیر از 2 خط می خورند. بعد سراغ مضارب عدد 3 بروید و همه را غیر از خود 3 خط بزنید بعد از آن مضارب 5 و مضارب 7 را هم خط بزنید توجه کنید 
اما نیازی به بررسی مضارب 11 نیست چون 
. حالا هر چه که خط نخورده عدد اول است.
به جای خط زدن در شکل زیر مضارب 2 را آبی، مضارب 3 را سبز، مضارب 5 را قرمز و مضارب 7 را بنفش کردیم. همه ی اعداد مشکی اول هستند.
جمع بندی
در این مقاله به آموزش اعداد اول پرداختیم با مفهوم تجزیه اعداد و شمارنده ها آشنا شدیم و روش های بدست آوردن بزرگترین شمارنده مشترک و کوچکترین مضرب مشترک را بررسی کردیم. در نهایت روش تشخیص اول بودن یک عدد و روش غربال را توضیح دادیم. در ضمن باید خاطر نشان کنیم که تاکنون فرمولی برای بدست آوردن همه اعداد اول کشف نشده است. امیدواریم از این آموزش لذت برده باشید. در صورت تمایل ما را از نظرات با ارزش تان در مورد مقاله اعداد اول در قسمت کامنت ها بهره مند کنید. در صورت علاقه به یادگیری در مورد سایر اعداد لطفا به مقاله اعداد حقیقی مراجعه کنید.
