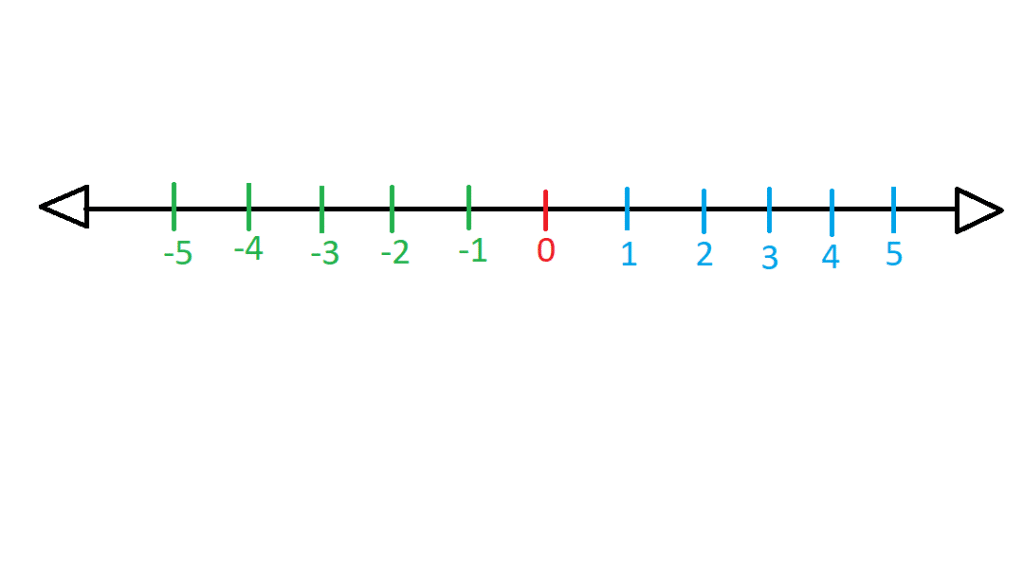جامع ترین آموزش درباره ی اعداد حقیقی و زیرمجموعه های آن

اعداد حقیقی در زبان انگلیسی $Real-Number$ نام دارند. در این مقاله به تعریف اعداد حقیقی می پردازیم. ابتدا به معرفی اعداد طبیعی، اعداد حسابی، اعداد صحیح، اعداد گویا و اعداد گنگ می پردازیم. در نهایت بررسی می کنیم این مجموعه اعداد چه رابطه ای با اعداد حقیقی دارند. در نهایت با محور اعداد حقیقی آشنا می شوید. امیدواریم از این آموزش لذت ببرید.

معرفی اعداد

ما در کودکی وسایل را می شمردیم و به این ترتیب با اعداد آشنا شدیم. اما بزرگتر که شدیم با شنیدن چیزهایی راجع به درصد سهام این که چه کسری از افراد یک شرکت تعلیق می شوند، ارتفاع از سطح دریا و… در اخبار متوجه شدیم اعداد دیگری غیر از اعدادی که با کمک شان می شمردیم هم وجود دارند. در ادامه انواع اعداد را معرفی می کنیم.

معرفی اعداد طبیعی

اعدادی که در کودکی بوسیله آنها شمردن را یاد گرفتیم اعداد طبیعی نام دارند. مجموعه ی اعداد طبیعی را با $\Bbb{N}=\{1,2,3, …\}$ نشان می دهند. بیشمار عدد طبیعی داریم. همانطور که از مجموعه اعداد طبیعی مشخص است کوچکترین عدد طبیعی عدد یک است و بزرگترین عدد طبیعی مشخص نیست. برای مطالعه در مورد اعداد طبیعی می توانید روی لینک اعداد طبیعی کلیک کنید.

معرفی اعداد حسابی

در صحبت های روزمره گاها از کلمه ای مثل هیچی استفاده می کنیم معادل هیچ در ریاضی عدد صفر است. اعداد حسابی شامل صفر و همه ی اعداد طبیعی است و با نماد $\Bbb{W}=\{0,1,2,3, …\}$ نشان داده می شود. کوچکترین عدد حسابی صفر است و بیشترین عدد حسابی مشخص نیست. برای مطالعه در مورد اعداد حسابی می توانید روی لینک اعداد حسابی کلیک کنید.

معرفی اعداد صحیح

حتما شنیده اید درصد رشد یک سهام منفی بود که به معنای کاهش آن سهام است. به قرینه اعداد طبیعی اعداد منفی می گویند. با قرینه اعداد طبیعی می توان چیزهایی مثل قرینه رشد، قرینه افزایش را بررسی کرد. حالا اگر اعداد منفی را به مجموعه اعداد حسابی اضافه کنیم مجموعه ی اعداد صحیح را ساخته ایم. اعداد صحیح را با $\Bbb{Z}=\{…,-2,-1,0,1,2, …\}$ نشان می دهیم کوچکترین عدد صحیح و بزرگترین عدد صحیح مشخص نیست. برای اینکه بیشتر راجع به اعداد صحیح مطالعه کنید با زدن روی لینک اعداد صحیح به می توانید به مقاله ی مربوطه مراجعه کنید.

معرفی اعداد گویا

اگر بخواهیم بخشی از یک چیز را بیان کنیم مثلا به زبان ریاضی بگوییم “از ده تا مهره 7 تاش قرمزه ” باید از کسر استفاده کنیم. به کسرها، اعداد گویا هم می گویند. برخلاف اعداد صحیح نمی توانیم همه ی اعضای اعداد گویا را بنویسیم. فقط باید بدانیم اعداد گویا در واقع نسبت دو عدد صحیح هستند. بزرگترین عضو و کوچکترین عضو اعداد گویا مشخص نیست. اعداد گویا را به صورت $\Bbb{Q}=\{\frac{a}{b}| a,b\in \Bbb{Z} , b\neq0\}$ نشان می دهند. بین هر دو عدد گویا بیشمار عدد گویا وجود دارد. برای اینکه بیشتر راجع به اعداد گویا مطالعه کنید با زدن روی لینک اعداد گویا به مقاله ی مربوطه مراجعه کنید.

معرفی اعداد گنگ

اعداد گنگ اعدادی هستند که نمی توان آنها را به صورت اعداد گویا نوشت. به طور کلی اعداد صحیح، طبیعی و حسابی را می توان بصورت گویا نوشت. مثلا عدد $2$ را می توان به صورت $\frac{2}{1}$ نوشت. اما اعداد اعشاری که قسمت اعشاری بیشمار و نامنظم دارند اعداد متعالی نامیده می شوند و نمی توان آنها را به صورت گویا نوشت (برای اطلاعات بیشتر راجع به این اعداد به مقاله اعداد اعشاری مراجع کنید.) مثل عدد پی $\pi$ و عدد نپر $e$ .

یک دسته دیگر از اعداد گنگ اعداد رادیکالی هستند که ریشه کامل ندارند مثلا $9$ ریشه دوم کامل دارد و عدد $3$ است. یا عدد $8$ ریشه سوم کامل دارد و عدد $2$ ریشه سوم $8$ است اما عدد $10$ ریشه دوم کامل ندارد پس $\sqrt{10}$ گنگ است. (برای اطلاعات بیشتر راجع به این اعداد به مقاله اعداد گنگ مراجع کنید.) اعداد گنگ را با $\Bbb{Q}^{'}$ یا $\Bbb{Q}^{c}$ نشان می دهند. بین هر دو عدد گنگ بیشمار عدد گنگ وجود دارد. همه ی اعداد گنگ را نمی توان روی محور نشان داد چون در هر پاره خطی از محور اعداد حقیقی بیشمار عدد گنگ و بیشمار عدد گویا وجود دارد. اما هر عدد گنگ از نوع رادیکالی را با روشی که در مقاله ی اعداد گنگ گفته شد می توان روی محور عدد حقیقی نشان داد.

معرفی اعداد حقیقی

تا الان با مجموعه های اعداد طبیعی، حسابی، صحیح، گویا و گنگ آشنا شدیم. با توجه به مطالبی که تا اینجا آموختیم متوجه می شویم که اعداد طبیعی زیرمجموعه اعداد حسابی و اعداد حسابی زیرمجموعه اعداد صحیح و اعداد صحیح زیرمجموعه اعداد گویا هستند. در واقع همه ی این مجموعه اعداد زیرمجموعه اعداد حقیقی هستند. در مبحث مجموعه ها این نکته به صورت $\Bbb{N}\subseteq \Bbb{W} \subseteq \Bbb{Z} \subseteq \Bbb{Q} \subseteq \Bbb{R}$ نوشته می شود. اعداد حقیقی شامل همه ی این اعداد یا به طور کلی اعداد گویا به انضمام اعداد گنگ می شود. به همه ی اعدادی که تا به اینجا بررسی کردیم اعداد حقیقی می گویند. با توجه به مبحث مجموعه ها می توان نشان داد $\Bbb{Q}^{'} \cup \Bbb{Q}=\Bbb{R}$

محور اعداد حقیقی

محور اعداد حقیقی یک خط است که از دو طرف تا بی نهایت ادامه دارد. هر نقطه روی این خط یک عدد حقیقی را نشان می دهد و هر عدد حقیقی حتما یک نقطه مخصوص به خود روی این خط دارد. محور اعداد حقیقی را در زیر می بینید:

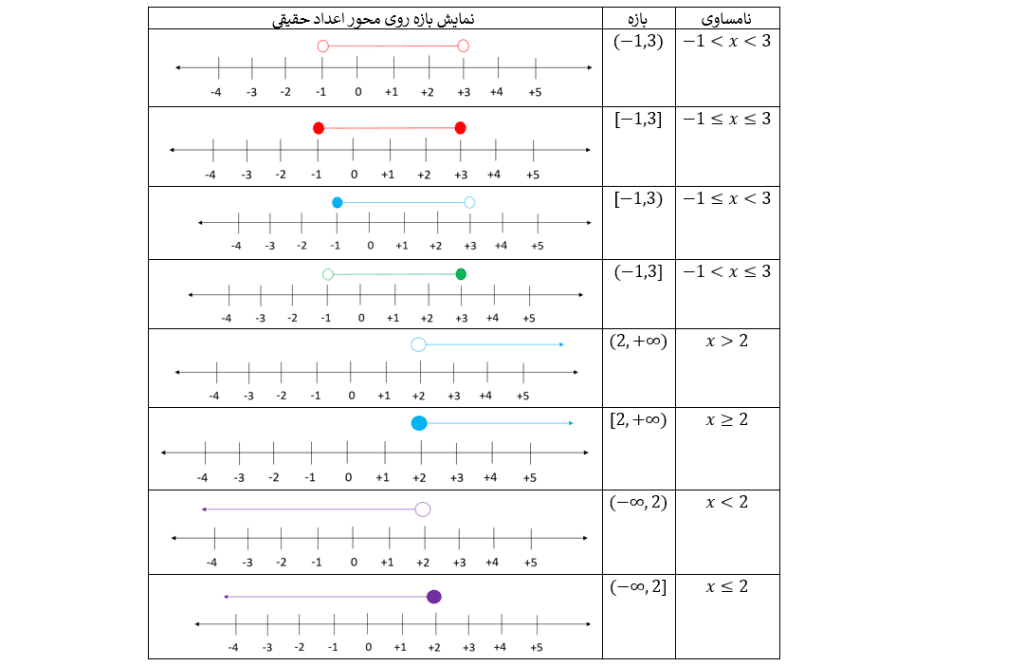
بوسیله بازه ها می توان نامساوی ها را نشان داد.

در جدول زیر مثال هایی از حالت های مختلف نامساوی ها و بازه و نمایش بازه روی محور اعداد حقیقی میبینید:

اعداد صحیح روی این خط نام گذاری شده اند اما همه ی اعداد گویا را نمی توان روی محور نشان داد. چون بین هر دو عدد گویایی که روی محور نشان دهیم بیشمار عدد گویا وجود دارد و نمی توان همه ی اعداد گویا را نشان داد.

همه ی اعداد را می توان بصورت علائم ریاضی نشان داد اما همانطور که در بخشهای قبلی توضیح داده شده اعداد گویا و گنگ را نمی توان به صورت یک بازه روی اعداد حقیقی نشان داد. در ادامه می بینیم برای هر نوع از اعداد چطور علائم ریاضی مربوطه را می نویسیم و چطور آنها را در صورت امکان روی محور اعداد حقیقی نشان می دهیم.

مثال: اعداد بین $-2$ و $+3$ را با توجه به شرط هر بخش تعیین کنید.

*اگر فقط اعداد طبیعی بین $-2$ و $+3$ مد نظر باشد:

جواب: می دانیم اعدادطبیعی بین $-2$ و $+3$ برابر با 2 و 1 می باشد. علائم ریاضی بصورت $\{x\in \Bbb{N} | -2 < x < 3\}$ می باشد.

*اگر فقط اعداد حسابی بین $-2$ و $+3$ مدنظر باشند:

جواب: می دانیم اعداد حسابی بین $-2$ و $+3$ برابر با 2 و 1 و صفر می باشد. علائم ریاضی بصورت $\{x\in \Bbb{W} | -2 < x < 3\}$ می باشد.

* اگر فقط اعداد صحیح بین $-2$ و $+3$ مدنظر باشند:

جواب: می دانیم اعداد صحیح بین $-2$ و $+3$ برابر با 2 و 1 و صفر و $-1$ می باشد. علائم ریاضی بصورت $\{x\in \Bbb{Z} | -2 < x < 3\}$ می باشد.

* اگر فقط اعداد گویا بین $-2$ و $+3$ مدنظر باشند:

جواب: همه ی اعداد گویا بین $-2$ و $+3$ را نمی توان نام برد. علائم ریاضی مربوط به اعداد گویا بصورت $\{x\in \Bbb{Q} | -2 < x < 3\}$ می باشد. نمی توان همه ی اعداد گویا در این بازه را روی محور اعداد حقیقی نشان داد.

* اگر فقط اعداد گنگ بین $-2$ و $+3$ مدنظر باشند:

جواب: همه ی اعداد گنگ بین $-2$ و $+3$ را نمی توان نام برد. علائم ریاضی مربوط به اعداد گنگ بصورت $\{x\in \Bbb{Q} ^{'} | -2 < x < 3\}$ است و نمی توان همه ی اعداد گنگ موجود در این بازه را روی محور اعداد حقیقی نشان داد.

* اگر فقط اعداد حقیقی بین $-2$ و $+3$ مدنظر باشند:

جواب: همه ی اعداد حقیقی بین $-2$ و $+3$ را نمی توان نام برد. علائم ریاضی مربوط به اعداد حقیقی بصورت $\{x\in \Bbb{R} | -2 < x < 3\}$ نمایش داده می شود.

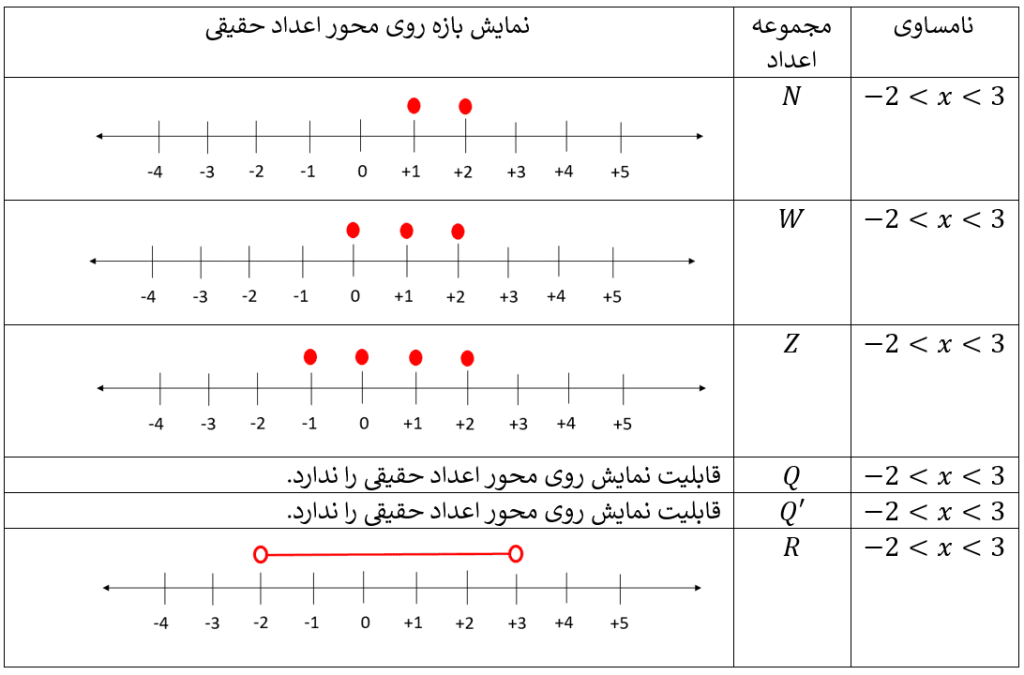
نمایش این مجموعه ها را در جدول زیر می بینید:

نکات مربوط به اعداد حقیقی

مثال: کدام صحیح و کدام غلط است.

*عددی وجود دارد که صحیح و گویا باشد. (صحیح) دلیل: همه ی اعداد صحیح گویا هستند.

*عددی وجود دارد که گویا و گنگ باشد. (غلط) دلیل: اعداد گویا و گنگ هیچ اشتراکی ندارند.

*عددی وجود دارد که حقیقی و گنگ باشد. (صحیح) دلیل: همه ی اعداد گنگ، حقیقی هستند.

*عددی وجود دارد که حقیقی و طبیعی باشد. (صحیح) دلیل: همه ی اعداد طبیعی ، حقیقی هستند.

*جمع دو عدد گنگ حتما عددی گنگ است. (غلط) دلیل: در جمع $\sqrt{10}+ (-\sqrt{10})=0$ حاصل صفر می شود که عددی گویا است و گنگ نیست.

*جمع عدد گنگ و عدد گویا عددی گنگ است. (صحیح)

*ضرب عدد گویای غیر صفر در عدد گنگ عددی گنگ است (صحیح)

*اگر یک عدد گنگ باشد معکوسش هم گنگ است. (صحیح)

نکته: تساوی های زیر همواره برقرارند. (اگر برای متوجه شدن این سوال به اطلاعات مربوط به مجموعه ها نیاز دارید لطفا به مقاله مربوطه مراجعه کنید)

$\Bbb{N}\cup \Bbb{Z}=\Bbb{Z} \, \, \, , \, \, \, \Bbb{R}-\Bbb{Q}^{'}=\Bbb{R}\cap {\Bbb{Q}^{'}}^{'}=\Bbb{R}\cap \Bbb{Q}=\Bbb{Q} \, \, \, , \, \, \, \Bbb{Z}\cap \Bbb{N}=\Bbb{N} \, \, \, , \, \, \, \Bbb{R}\cap \Bbb{Q}^{'}=\Bbb{Q}^{'} \, \, \, , \, \, \, \Bbb{N}\cap \Bbb{Q}=\Bbb{N}$

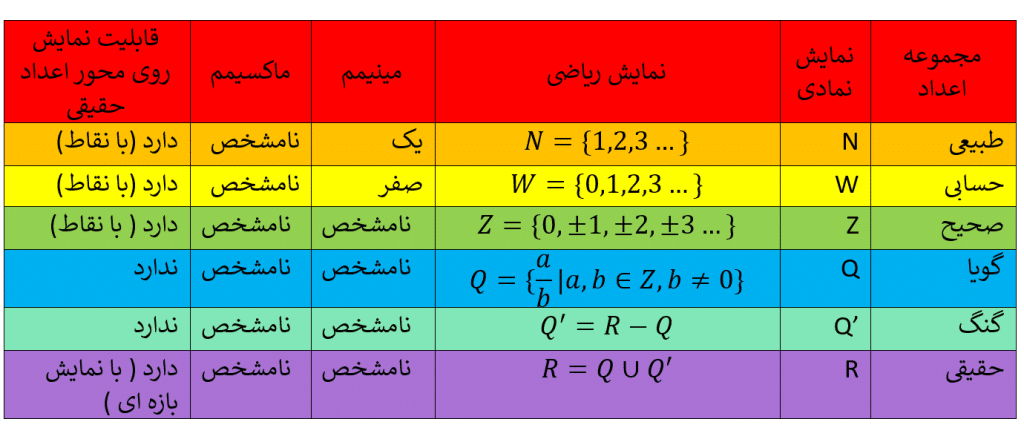
در جدول زیر همه ی مجموعه های عددی را به طور کلی می بینید:

جمع بندی

تا اینجا دیدیم همه ی اعدادی که تا پایان دبیرستان می خوانیم اعداد حقیقی هستند. در واقع اعداد حقیقی اعدادی هستند که حداقل یک مصداق در فیزیک کلاسیک دارند. به اعداد غیرحقیقی اعداد مختلط می گویند که در این مقاله راجع به آن صحبت نشده است. در این مقاله به معرفی زیرمجموعه های اعداد حقیقی یعنی اعداد طبیعی، اعداد حسابی، اعداد صحیح، اعداد گویا و اعداد گنگ پرداختیم که البته در مورد هر کدام مقاله ی جداگانه ای ایجاد شده که با زدن بر روی هر کدام از لینک ها می توانید به مقاله ی مرتبط دست پیدا کنید. لطفا نظرات خود را در مورد مقاله اعداد حقیقی در قسمت کامنت ها بیان کنید.

جامع ترین آموزش درباره ی اعداد حقیقی و زیرمجموعه های آن

معرفی اعداد

معرفی اعداد طبیعی

معرفی اعداد حسابی

معرفی اعداد صحیح

معرفی اعداد گویا

معرفی اعداد گنگ

معرفی اعداد حقیقی

محور اعداد حقیقی

نکات مربوط به اعداد حقیقی

دیدگاهتان را بنویسید لغو پاسخ

آخرین مطالب وبلاگ

دنباله های عددی

تابع خطی و معادله خط

تابع و دامنه و برد آن

تعیین علامت

عبارت و معادله گویا

معادله درجه دوم

معادله

عبارت جبری

قدرمطلق

دوره ها

دسترسی سریع

دسترسی سریع

مقالات مادر