کامل ترین آموزش در مورد اعداد رادیکالی و جذر و ریشه

جذر و ریشه گرفتن یا به انگلیسی $Square-root$ عملی است که اعداد رادیکالی با فرجه های متفاوت را می سازد. در این مقاله به معرفی اعداد رادیکالی ساده کردن اعداد رادیکالی نمایش آنها روی محور اعداد حقیقی می پردازد. اگر یک آموزش کامل در مورد اعداد رادیکالی می خواهید این مقاله را از دست ندهید. در این مقاله همچنین به آموزش نحوه جمع و تفریق و ضرب و تقسیم کردن اعداد رادیکالی می پردازیم. گویا کردن مخرج کسر و بدست آوردن اعداد با توان گویا نیز در این آموزش گنجانده شده است. امیدواریم از این آموزش نهایت لذت و بهره را ببرید.

معرفی و تعریف جذر و ریشه

در تساوی $3^{2}=9$ عدد $9$ را توان دوم یا مجذور عدد $3$ و عدد $3$ را ریشه دوم یا جذر عدد $9$ می نامند.

عدد $-3$ هم ریشه دوم عدد $9$ است چون $(-3)^{2}=9$

برای نمایش ریشه دوم از نماد $\sqrt{}$ (بخوانید رادیکال) استفاده می کنیم. ریشه های دوم $9$ را با $\sqrt{9}$ و $-\sqrt{9}$ نشان می دهیم. به عبارت دیگر $\sqrt{9}=3$ و $-\sqrt{9}=-3$ ریشه های دوم یا جذرهای عدد 9 هستند.

به طور کلی اگر $b$ یک عدد حقیقی مثبت باشد، $\sqrt{b}$ و $-\sqrt{b}$ را ریشه های دوم $b$ می نامند. ولی اگر $b$ یک عدد حقیقی منفی باشد می گوییم $b$ ریشه دوم ندارد.

به طور کلی اگر $b$ یک عدد حقیقی باشد، $\sqrt[3]{b}$ را ریشه سوم $b$ یا $b$ به فرجه سه می نامند. هر عدد فقط یک ریشه سوم دارد.

نکته : جذر ِ مجذور ِ یک عدد برابر با قدرمطلق آن عدد است.

$\sqrt{x^{2}}=| x|$

برای محاسبه ی جذر و ریشه باید به نکات زیر توجه کنیم:

مجذور عدد صفر همان صفر است.

اگر عددی صفر نباشد، توان دوم آن همواره مثبت است.

هر عدد مثبت داراری دو ریشه دوم است که یکی از آنها قرینه دیگری است. اعداد منفی ریشه دوم ندارند.

هر عدد مثبت دارای دو ریشه چهارم است که قرینه یکدیگرند. اعداد منفی ریشه چهارم ندارند.

هر عدد حقیقی دارای یک ریشه پنج است ریشه پنجم هر عدد با خود عدد هم علامت است.

چطور اعداد رادیکالی را روی محور نمایش دهیم؟

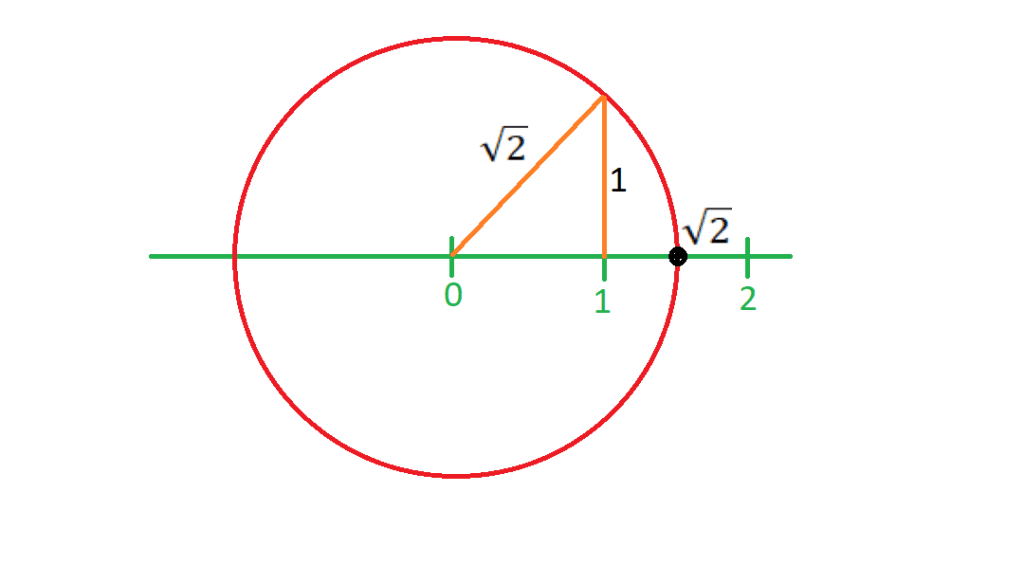
اعداد رادیکالی را می توان روی محور اعداد حقیقی نمایش داد برای این کار باید از فیثاغورث (برای خواندن درباره ی رابطه ی فیثاغورس به مقاله ی مثلث رجوع کنید) کمک بگیریم. مثلا برای نمایش $\sqrt{2}$ روی محور اعداد، ابتدا باید عدد 2 را بصورت مجموع دو عدد مربع کامل بنویسیم $1^{2}+1^{2}=2$ حالا می توانیم یک مثلث قائم الزاویه به اضلاع قائمه 1 و 1 رسم کنیم در نتیجه وتر این مثلث برابر با $\sqrt{2}$ می شود. به شکل زیر توجه کنید تا متوجه شوید چطور نقطه مربوط به $\sqrt{2}$ را با کمان زدن روی محور پیدا می کنیم.

نکته مهم: اعداد رادیکالی را می توان روی محور اعداد حقیقی نمایش داد اما برخلاف اعداد صحیح نمی توان همه ی اعداد رادیکالی را یکجا روی محور اعداد حقیقی نمایش داد چون بین هر دو عدد گنگ که روی محور نشان دهیم قطعا بیشمار عدد گنگ و بیشمار عدد گویا وجود دارد.

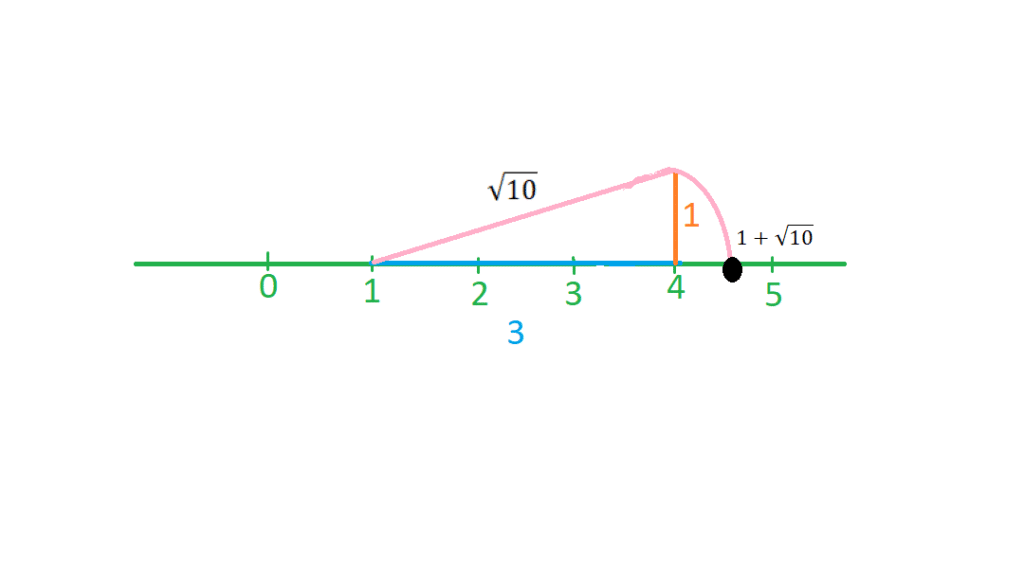
مثال: برای پیدا کردن نقطه مربوط به $1+\sqrt{10}$ هم از نقطه $1$ شروع می کنیم و یک مثلث قائم الزاویه براساس رابطه $1^{2}+3^{2}=10$ رسم می کنیم پس اضلاع قائمه 1 و 3 می باشند و وتر برابر $\sqrt{10}$ می شود. با توجه به شکل زیر نقطه $B$ نشان دهنده ی $1+\sqrt{10}$ می باشند.

چطور ضرب و تقسیم اعداد رادیکالی را انجام دهیم؟

برای ضرب اعداد رادیکالی در هم باید اعداد پشت رادیکال را در هم ضرب کنیم و اعداد زیر رادیکال را در هم ضرب کنیم. مثلا

$a\sqrt{b}\times c\sqrt{d}=(a\times c)\sqrt{b\times d}$

به همین ترتیب برای تقسیم هم دو عدد پشت رادیکال را تقسیم می کنیم و اعداد زیر رادیکال را تقسیم می کنیم. مثلا

$m\sqrt{p}\div n\sqrt{q}=(m\div n)\sqrt{p \div q})=\frac{m}{n}\sqrt{\frac{p}{q}}$

اگر $p$ و $q$ هر دو مثبت باشند می توان گفت:

$\sqrt{\frac{p}{q}}=\frac{\sqrt{p}}{\sqrt{q}}$

به طور کلی برای هر دو عدد $a$ و $b$ داریم:

$\sqrt[3]{ab}=\sqrt[3]{a}\sqrt[3]{b}$

همچنین اگر $b\neq 0$ داریم :

$\sqrt[3]{\frac{a}{b}}=\frac{\sqrt[3]{a}}{\sqrt[3]{b}}$

جذر تقریبیِ یک عدد رادیکالی چگونه بدست می آید؟

برخی از اعداد رادیکالی مقدار دقیق شان قابل محاسبه است اما برخی دیگر از اعداد رادیکالی هیچ گاه مقدار دقیق شان بدست نمی آید به این دسته از اعداد رادیکالی، اعداد گنگ گفته می شود.

در حالتی که جذر اعداد مشخص است باید با توجه به توان دوم اعداد که به در ذهن داریم به محاسبه جذر اعداد بپردازیم. برای اینکار اعداد مجذور کامل زیر را برای شما نوشتیم:

$0^{2}=0\,,\,\,1^{2}=1\,,\,\,2^{2}=4\,,\,\,3^{2}=9$

$4^{2}=16\,,\,\,5^{2}=25\,,\,\,6^{2}=36\,,\,\,7^{2}=49$

$8^{2}=64\,,\,\,9^{2}=81\,,\,\,10^{2}=100$

$11^{2}=121\,,\,\,12^{2}=144\,,\,\,13^{2}=169$

$14^{2}=196\,,\,\,15^{2}=225\,,\,\,16^{2}=256$

$17^{2}=289\,,\,\,18^{2}=324$

$19^{2}=361\,\,\,,\,\,\,20^{2}=400$

حالا اگر سوال بپرسد $\sqrt{0.36}$ چند است؟ می نویسیم $\sqrt{\frac{36}{100}}$ که حالا با توجه به نکاتی که بالاتر گفته شد می نویسیم $\sqrt{\frac{36}{100}}=\frac{\sqrt{36}}{\sqrt{100}}$ که از تساوی های بالا می دانیم $\frac{\sqrt{36}}{\sqrt{100}}=\frac{6}{10}$ پس می توان گفت مقدار دقیقی برای این سوال وجود دارد و برابر با $\sqrt{0.36}=0.6$ است.

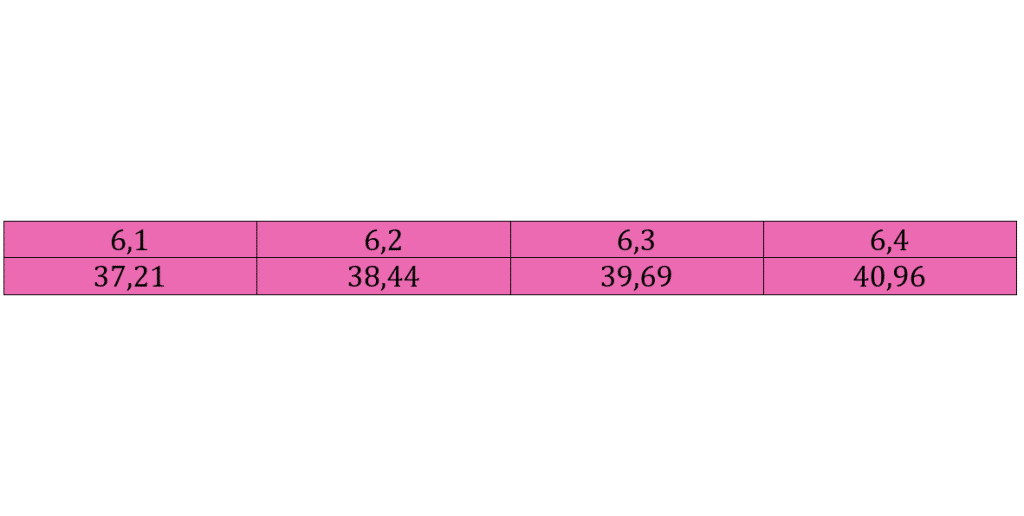
اما اگر این سوال را در مورد عدد $\sqrt{39}$ بپرسند جواب دقیقی برای این سوال وجود ندارد و باید به دنبال مقدار تقریبی آن باشیم برای این کار ابتدا باید دو عدد صحیح که $\sqrt{39}$ بین آنها است را پیدا کنیم با توجه به اعداد توان دار بالا داریم: $6 < \sqrt{39} < 7$ پس می توان گفت رادیکال $39$ حدودا شش و خورده است. حالا برای اینکه بفهمیم که این خورده چقدر است باید $6.5^{2}$ را حساب کنیم که برابر با $42.25$ است حالا چون $39 < 42.25$ پس می فهمیم $\sqrt{39} < 6.5$ . آنقدر این کار را ادامه می دهیم تا بفهمیم $\sqrt{39}$ بین کدام دو عدد تا یک رقم اعشار قرار دارد.

طبق این جدول داریم : $6.2< \sqrt{39} < 6.3$ وقتی به این نامساوی رسیدیم حتما مقدار کمتر را بعنوان جذر تقریبی در نظر می گیریم:

$\sqrt{39} \cong 6.2$

چطور عبارت رادیکالی را ساده کنیم؟

اعداد رادیکالی که مقدار زیر رادیکال آنها اعداد مرکب هستند را می توان ساده کرد. برای این کار این اعداد را به صورت حاصل ضرب اعداد اول می نویسیم و آنهایی که توان زوج دارند را از زیر رادیکال بیرون می آوریم به این ترتیب که توان آنها را نصف می کنیم. مثلا در عدد $\sqrt{12}$ می توانیم عدد $12$ را به صورت $12=2^{2} \times 3$ تجزیه کنیم. حالا کافی است به دستورالعمل بالا عمل کنیم داریم: $\sqrt{12}=2^{1}\sqrt{3}$ . یا در عدد $\sqrt{72}$ می توانیم عدد $72$ را به صورت $72=2^{3}\times 3^{2}$ تجزیه کنیم. حالا کافی است به دستورالعمل بالا عمل کنیم داریم:

$\sqrt{72}=2\times 3\sqrt{2}=6\sqrt{2}$

جمع و تفریق رادیکال ها چطور انجام دهیم؟

برای اینکه بتوان دو عدد رادیکالی را جمع یا تفریق کرد باید قسمت رادیکالی یکسانی داشته باشند یا بتوان قسمت رادیکالی شان را با ساده کردن، که در بالاتر توضیح داده شده، یکسان کرد مثلا

$a\sqrt{m}+b\sqrt{m}=(a+b)\sqrt{m}$

اما اگر سوال بصورت $a\sqrt{m}+b\sqrt{n}$

باشد عبارت سوال را نمی توان ساده تر کرد.

گویا کردن مخرج کسر چطور انجام می شود؟

در اعداد کسری که مخرج رادیکالی دارند بهتر است مخرج کسرشان را گویا کرد. این کار را می توان با کمک به توان رساندن انجام داد. مثلا در عدد $\frac{3}{\sqrt{2}}$ برای گویا کردن مخرج کسر کافی است مخرج را به توان دو برسانیم یعنی یک بار در خودش ضرب کنیم داریم :

$\frac{3}{\sqrt{2}}=\frac{3\times \sqrt{2}}{\sqrt{2}\times \sqrt{2}}=\frac{3 \sqrt{2}}{2}$

در عدد $\frac{3}{\sqrt[5]{7}}$ برای گویا کردن مخرج کسر کافی است مخرج را به توان 5 برسانیم یا 4 بار دیگر در خودش ضرب کنیم:

$\frac{3}{\sqrt[5]{7}}=\frac{3\times \sqrt[5]{7^{4}}}{\sqrt[5]{7}\times\sqrt[5]{7^{4}} }=\frac{3\sqrt[5]{7^{4}}}{7}$

مقایسه اعداد رادیکالی

برای مقایسه اعداد رادیکالی کافی است که حدس بزنیم آن اعداد حدودا چند هستند و بعد مقایسه را انجام دهیم. برای اینکه بتوانیم حدس بزنیم مانند آنچه که در بالاتر گفته شد باید متوجه شویم که آن عدد رادیکالی بین کدام دو عدد صحیح متوالی قرار دارد. مثلا $\sqrt{17}$ بین 4 و 5 است پس حدودا برابر چهار و خورده هست در حالی که $\sqrt[3]{30}$ بین $\sqrt[3]{27}=3$ و $\sqrt[3]{64}=4$ است پس حدودا سه و خورده است پس می توان گفت:

$\sqrt[3]{30} < \sqrt{17}$

نکته: به طور کلی اگر $0 < a < b \,\,\,,\,\,\, n \in \Bbb{N}$ در نتیجه

$\sqrt[n]{a} < \sqrt[n]{b}$

اما اگر بخواهیم ریشه های یک عدد را با هم مقایسه کنیم با توجه به اینکه آن عدد در چه بازه ای قرار دارد جواب متفاوت است. داریم:

اگر $x < -1$ باشد آنگاه :

$x < \sqrt[3]{x} < \sqrt[5]{x} < \sqrt[7]{x} < …$

اگر $-1 < x < 0$ باشد آنگاه :

$x > \sqrt[3]{x} > \sqrt[5]{x} > \sqrt[7]{x} > …$

اگر $0 < x < 1$ باشد آنگاه :

$x < \sqrt[2]{x} < \sqrt[3]{x} < \sqrt[4]{x} < …$

اگر $x > 1$ باشد آنگاه :

$x > \sqrt[2]{x} > \sqrt[3]{x} > \sqrt[4]{x} > …$

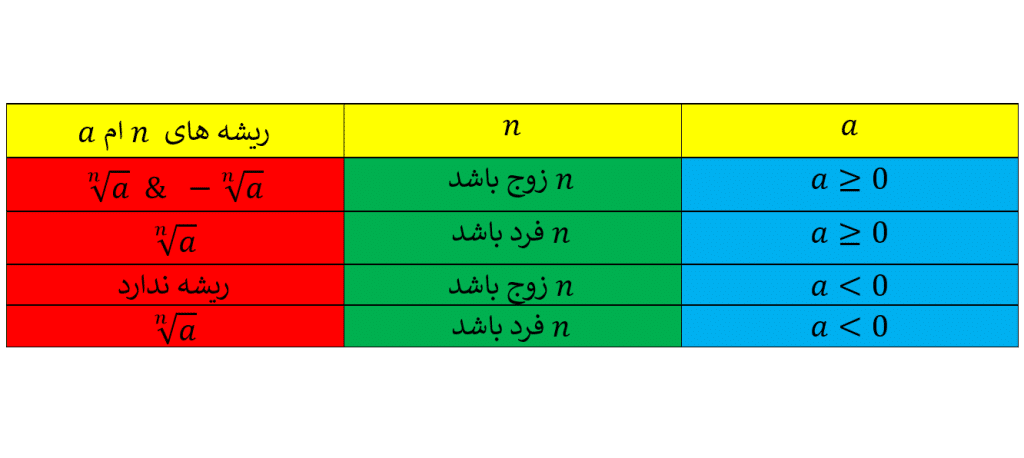
ریشه n ام یک عدد چطور تعریف می شود؟

اگر $n \ge 2$ یک عدد طبیعی باشد، $b$ را یک ریشه $n$ ام عدد $a$ می نامیم، هرگاه:

$b^{n}=a$

در حالت کلی تر درباره ریشه های $n$ ام $(n \in \Bbb{N})$ عددی مانند $a$ می توان گفت:

نکته: در حالت کلی برای هر $n \ge 2$ داریم:

$\sqrt[n]{a^{n}}=\begin{cases}| a | & n=2k \\ a & n=2k+1 \end{cases}$

اعداد با توان گویا

در اعداد با توان های گویا اعدادی داریم که توان شان اعداد کسری یا گویا هستند. مثلا در عدد $a^{\frac{m}{n}}$ ما یک عدد با توان گویا داریم که در آن $a > 0$ و $m$ و $n$ دو عدد طبیعی هستند. می توان این عدد را به صورت $\sqrt[n]{a^{m}}$ یا $(a^{m})^{\frac{1}{n}}$ نیز نوشت. در واقع داریم:

$a^{\frac{m}{n}}=\sqrt[n]{a^{m}}=(a^{\frac{1}{n}})^{m}=(a^{m})^{\frac{1}{n}}=(\sqrt[n]{a})^{m}$

همچنین $a^{-\frac{m}{n}}$ نیز به صورت زیر تعریف می شود :

$a^{-\frac{m}{n}}=\frac{1}{a^{\frac{m}{n}}}$

مثلا

$3^{\frac{5}{7}}=(3^{\frac{1}{7}})^{5}=(3^{5})^{\frac{1}{7}}=(\sqrt[7]{3})^{5}=\sqrt[7]{3^{5}}$

حالا می دانیم یک عدد با ریشه $n$ ام را می توان به صورت یک عدد با توان گویا نوشت. برای هر عدد طبیعی $n \ge 2$ داریم:

$a^{\frac{1}{n}}=\sqrt[n]{a}$

اگر $a < 0$ پس $a^{\frac{1}{n}}$ را تعریف نمی کنیم.

نکته: اگر $r$ و $s$ دو عدد گویا باشند و $a$ و $b$ اعدادی مثبت باشند، داریم:

$a^{r}\times a^{s}=a^{r+s} \,\,\,,\,\,\, (a^{r})^{s}=a^{rs}$

$(ab)^{r}=a^{r}\times b^{r}$

مثلا $3^{\frac{5}{7}}\times 3^{\frac{2}{7}}=3^{\frac{7}{7}}=3$

جمع بندی

در این مقاله به آموزش مبحث جذر و ریشه پرداختیم. نمایش اعداد رادیکالی روی محور اعداد حقیقی، ساده کردن اعداد رادیکالی و گویا کردن مخرج کسرها از مطالبی بود که در این آموزش به آن پرداخته شده بود. همچنین نحوه بدست آوردن جذر تقریبی و جمع و تفریق و ضرب و تقسیم اعداد رادیکالی نیز در این آموزش رایگان بیان شده است. اگر تمایل به آموزش در مورد اعداد توان دار دارید لطفا به مطالعه مقاله اعداد توان دار بپردازید. همچنین باید بدانید برخی از اعداد رادیکالی گویا و برخی گنگ هستند اگر می خواهید در این مورد بیشتر بدانید به مقاله اعداد گنگ مراجعه فرمایید. لطفا ما را از نظرات باارزش تان در مورد مقاله جذر و ریشه در قسمت کامنت ها بهره مند کنید.

کامل ترین آموزش در مورد اعداد رادیکالی و جذر و ریشه

معرفی و تعریف جذر و ریشه

چطور اعداد رادیکالی را روی محور نمایش دهیم؟

چطور ضرب و تقسیم اعداد رادیکالی را انجام دهیم؟

جذر تقریبیِ یک عدد رادیکالی چگونه بدست می آید؟

چطور عبارت رادیکالی را ساده کنیم؟

جمع و تفریق رادیکال ها چطور انجام دهیم؟

گویا کردن مخرج کسر چطور انجام می شود؟

مقایسه اعداد رادیکالی

ریشه n ام یک عدد چطور تعریف می شود؟

اعداد با توان گویا

دیدگاهتان را بنویسید لغو پاسخ

آخرین مطالب وبلاگ

دنباله های عددی

تابع خطی و معادله خط

تابع و دامنه و برد آن

تعیین علامت

عبارت و معادله گویا

معادله درجه دوم

معادله

عبارت جبری

قدرمطلق

دوره ها

دسترسی سریع

دسترسی سریع

مقالات مادر