جامع ترین آموزش درمورد احتمال هر آنچه که لازم است درباره ی احتمال بدانید

احتمال علمی است که به ما کمک می کند که میزان شانس یک اتفاق تصادفی را بدست بیاوریم. در این مقاله به آموزش احتمال یک پیشامد، قانون احتمال کل، احتمال شرطی، اصول احتمال پرداختیم. احتمال های غیرهمشانس، قانون بیز، پیشامدهای ناسازگار و مستقل را بیان کردیم. همه ی اطلاعاتی که درباره احتمال از ابتدایی تا کنکور لازم دارید را می توانید در این مقاله بیابید بنابراین اگر یک دانش آموز یا یک معلم هستید این آموزش رایگان را از دست ندهید.

احتمال را تعریف کنید

آنگاه که با جامعه ای ناشناخته سر و کار داریم، شناختن جامعه با استفاده از نمونه ها و داده ها یک کار آماری است، ولی اگر جامعه را با جزئیات مورد نیاز بشناسیم و بخواهیم بدانیم نمونه هایی از آن جامعه چگونه خواهند بود، علم احتمال به کمک ما می آید.

علم احتمال: بررسی یک نمونه نامعلوم از یک جامعه معلوم

علم آمار: شناختن جامعه نامعلوم، با استفاده از نمونه های جمع آوری شده معلوم

احتمال رخداد یک پیشامد (اندازه گیری شانس در احتمالات هم شانس)

وقتی یک سکه می اندازیم دو حالت هم شانس ممکن است اتفاق بیفتد ، یا سکه رو می آید یا پشت و چون در یک حالت از این دو حالتِ ممکن ، سکه رو می آید؛ پس احتمال رو آمدن سکه $\frac{1}{2}$ است.

به این ترتیب برای بیان اندازه شانس رخ دادن یک اتفاق، از یک عدد استفاده کرده ایم که احتمال رخ دادن آن اتفاق نامیده می شود.

به پدیده ها یا آزمایش هایی که نتیجه آنها قبل از اجرای آزمایش به طور قطع مشخص نیست، پدیده یا آزمایش تصادفی می گویند. در پدیده های تصادفی از همه نتیجه های ممکن اطلاع داریم اما از اینکه کدام حالت قطعا رخ می دهد، اطمینان نداریم. به هر یک از نتایج ممکن برای یک آزمایش تصادفی، برآمد می گوییم.

برای اینکه احتمال رخ دادن یک اتفاق را به دست آوریم ، ابتدا همه ی حالت های ممکن را می یابیم ، سپس حالت های مورد نظر را از میان حالت های ممکن پیدا می کنیم. احتمال رخ دادن اتفاق مورد نظر برابر است با نسبت تعداد حالت های مورد نظر یا حالت های مطلوب به تعداد حالت های ممکن.

مثلا احتمال اینکه تاس بیندازیم و عدد 3 بیاید $\frac{1}{6}$ است. چون کلا 6 تا عدد ممکن است بیاید و ما فقط یکی از آن را می خواهیم. پس احتمال برابر $\frac{1}{6}$ است.

برای اینکه احتمال رخ دادن هر پیشامد را بیابیم، تعداد حالت های منجر به آن اتفاق را بر تعداد کل حالت ها تقسیم می کنیم.

مثال: اگر یک تاس و یک سکه را با هم بیندازیم احتمال اینکه سکه رو بیاید و تاس فرد بیاید چیست؟

جواب: کل حالاتی که اگر تاس بیندازیم ممکن است بیاید برابر با $\{ 1,2,3,4,5,6\}$ است. و کل حالاتی که ممکن است با انداختن سکه پیش بیاید رو یا پشت آمدن سکه است. بیابراین برای تاس 6 حالت ممکن است و برای سکه 2 حالت ممکن است. بنابراین طبق اصل ضرب (که در مقاله ترکیبیات می توانید آن را یاد بگیرید) در کل $6 \times 2=12$ حالت داریم.

در گام دوم حل سوال باید بدانیم دوست داریم چه اتفاقی بیفتد. طبق صورت سوال دوست داریم تاس فرد بیاید که 3 حالت دارد و سکه رو بیاید که 1 حالت دارد. پس در کل $3 \times 1=3$ حالت مطلوب داریم.

پس احتمال اینکه سکه رو بیاید و تاس فرد بیاید برابر است با $\frac{3}{12}=\frac{1}{4}$ است.

می توان گفت اگر مجموعه شامل همه حالت های ممکن را $S$ ، مجموعه شامل همه ی حالت های مطلوب را $A$ و احتمال رخ دادن پیشامد $A$ را با نماد $P(A)$ نشان دهیم، دستور احتمال (احتمال برابر است با تعداد حالات مطلوب به تعداد حالات کل ) به صورت $P(A)=\frac{n(A)}{n(S)}$ نوشته می شود. این فرمول برای احتمال های همشانس کاربرد دارد یعنی احتمال اینکه در پرتاب یک سکه رو بیاید با اینکه پشت بیاید یکسان باشد.

به طور کلی اگر $S$ فضای نمونه ای یک آزمایش تصادفی باشد و $A \subseteq S$ یک پیشامد در فضای $S$ باشد، احتمال رخداد پیشامد $A$ یعنی $P(A)$ که به صورت زیر تعریف می شود:

$P(A)=\frac{n(A)}{n(S)} ,\, 0 \le P(A) \le 1,\,P(A) \in \Bbb{R}$

هر چه $P(A)$ به عدد 1 نزدیکتر باشد شانس رخداد $A$ بیشتر و هر چه به صفر نزدیکتر باشد، شانس رخداد $A$ کمتر است.

برای هر دو پیشامد $A$ و $B$ از فضای نمونه ای $S$ ، همواره تساوی زیر برقرار است:

$P(A \cup B)=P(A)+P(B)-P(A \cap B)$

به هر یک از زیرمجموعه های فضای نمونه $S$ یک پیشامد می گویند. از آنجا که $\phi \subseteq S$ پس $\phi$ یک پیشامد روی $S$ است و آن را پیشامد غیرممکن ( نشدنی ) می نامیم. همچنین $S \subseteq S$ پس $S$ هم یک پیشامد است که آن را پیشامد حتمی می نامیم.

به $A$ و $A^{'}$ دو پیشامد متمم می گویند.

پیشامدهای تصادفی و برخی اعمال روی آنها

اگر $A$ و $B$ پیشامدهایی در فضای نمونه ای $S$ باشند، در این صورت هر یک از پیشامد های $A \cup B$ و $A \cap B$ و $A-B$ در فضای نمونه ای $S$ به صورت های زیر توصیف می شوند:

اجتماع دو پیشامد: پیشامد $A \cup B$ وقتی رخ می دهد ( اتفاق می افتد) که حداقل یکی از دو پیشامد رخ بدهد. ( یا $A$ رخ بدهد یا $B$ رخ بدهد یا هر دو رخ بدهد)

اشتراک دو پیشامد: پیشامد $A \cap B$ وقتی رخ می دهد که دو پیشامد با هم رخ بدهند (هم پیشامد $A$ رخ بدهد و هم پیشامد $B$ رخ بدهد)

تفاضل دو پیشامد: پیشامد $A-B$ وقتی رخ می دهد که پیشامد $A$ رخ بدهد و پیشامد $B$ رخ ندهد.

متمم یک پیشامد: اگر $A$ یک پیشامد از فضای نمونه ای $S$ باشد، متمم پیشامد $A$ که با $A^{'}$ یا $A^{c}$ نمایش داده می شود ، وقتی رخ می دهد که پیشامد $A$ رخ ندهد؛ بنابراین

$A \cup A^{'}=S \,\,\,,\,\,\, A \cap A^{'}=\phi$

چه زمانی دو پیشامد ناسازگارند؟

تعریف دو پیشامد ناسازگار: اگر $A$ و $B$ دو پیشامد از فضای نمونه ای $S$ باشند و $A\cap B=\phi$ در این صورت $A$ و $B$ را دو پیشامد ناسازگار می نامیم. در واقع دو پیشامد ناسازگار هیچ گاه با هم رخ نمی دهند.

تذکر: همواره هر پیشامد تصادفی با متمم اش ناسازگار است.

نکته: اگر $A$ و $B$ و $C$ سه پیشامد از فضای نمونه ای $S$ باشند، این سه پیشامد را دو به دو ناسازگار می گوییم هرگاه شرایط زیر برقرار باشد.

$B \cap C=\phi \,,\,A \cap C= \phi \,,\, A \cap B=\phi$

تعمیم پیشامدهای ناسازگار: پیشامدهای $A_{1}$ و $A_{2}$ و … و $A_{n}$ را دو به دو ناسازگار گوییم هرگاه هیچ دو تایی از آنها نتوانند با هم رخ دهند در این صورت داریم:

$P(A_{1}\cup A_{2} \cup …\cup A_{n})$

$=P(A_{1})+P(A_{2})+…+P(A_{n})$

اگر $A$ و $B$ دو پیشامد ناسازگار باشند، این تساوی به صورت زیر نوشته می شود:

$P(A \cup B)+P(A)+P(B)$

چه زمانی دو پیشامد، مستقل اند؟

پیشامد $A$ از پیشامد $B$ مستقل است ، هرگاه وقوع $B$ بر احتمال وقوع $A$ تاثیر نگذارد.

مستقل بودن $A$ از $B$ معادل است با اینکه

$P(A \cap B)=P(A) \times P(B)$

دو پیشامد $A$ و $B$ از هم مستقل نیستند اگر و تنها اگر

$P(A \cap B)\neq P(A) \times P(B)$

اگر پیشامدی مانند $B$ با وقوع پیشامد $A$ هیچ ارتباطی نداشته باشد می توان به سادگی نشان داد که وقوع پیشامد $B$ احتمال وقوع پیشامد $A$ را تغییر نمی دهد بنابراین دو پیشامد مذکور از هم مستقل اند.

اگر در ظاهر $A$ و $B$ پیشامدهایی باشند که وقوع شان با هم در ارتباط است ، نمی توان به طور قطع گفت که $A$ و $B$ مستقل نیستند.

دو پیشامدی که مستقل نباشند وابسته نامیده می شوند.

ترجمه زبان گزاره ها به زبان مجموعه ها

برای ترجمه زبان گزاره ها به زبان مجموعه ها باید بدانیم به مجموعه ی کل حالات ممکن فضای نمونه می گویند. به هر عضو فضای نمونه یک برآمد می گویند.

با توجه به رخ دادن یک پیشامد می فهمیم که:

اگر $A_{1}$ زیرمجموعه $A_{2}$ باشد رخ دادن $A_{1}$ رخ دادن $A_{2}$ را نتیجه می دهد.

رخ دادن پیشامد $A_{1}\cap A_{2}$ یعنی هر دو پیشامد $A_{1}$ و $A_{2}$ رخ دهد.

رخ دادن پیشامد $A_{1} \cup A_{2}$ یعنی دست کم یکی از دو پیشامد $A_{1}$ و $A_{2}$ رخ دهد.

تشخیص فضای نمونه

در صورتی که آزمایشی متشکل از دو آزمایش با فضاهای نمونه $S_{1}$ و $S_{2}$ باشد فضای نمونه آن $S_{1}\times S_{2}$ است مشابه این موضوع برای هر تعداد آزمایش همزمان نیز درست است.

اصول احتمال چیست؟

در حالت کلی شناختن فضای نمونه برای توصیف یک رویداد تصادفی کافی نیست. علاوه بر آن لازم است که بدانیم احتمال رخ دادن پیشامدهای مختلف که زیرمجموعه های فضای نمونه اند، چقدر است

مشهور است که دالامبـر دائرةالمعارف نویس فرانسوی قرن هجدهم، تصور می کرد که اگر یک سکه را دو بار پرتاب کنیم، احتمال اینکه دقیقا یک بار رو بیاید، برابر یک سوم است. او اینگونه استدلال میکرد: در چنین آزمایشی سه حالت وجود دارد: “هر دو رو”، “هر دو پشت” و “یک بار رو و یک بار پشت”. در نتیجه احتمال وقوع هر یک از این حالات یک سوم است.

نکته این است در یک فضای نمونه برآمدهای مختلف ممکن است احتمال برابر نداشته باشند. در این حالت، محاسبه احتمال برآمدها و پیشامدها ممکن است ساده نباشد، ولی احتمال پیشامدهای مختلف حتما باید ویژگیهایی داشته باشد که به آنها اصول احتمال می گویند:

برای هر پیشامد مثل $A$ ، احتمال رخ دادن آن با $P(A)$ نمایش داده می شود که عددی حقیقی در بازه $[0,1]$ است. اصول احتمال عبارتند از :

$P(S)=1\,\,\,,\,\,\, P(\phi)=0$

$P(A^{'})=1-P(A)$

$P(A-B)=P(A)-P(A \cap B)$

$P(A-B)=P(A\cup B)-P(B)$

$P(A \cup B)=P(A)+P(B)-P(A\cap B)$

احتمال غیر هم شانس

هر زیر مجموعه تک عضوی از فضای نمونه ای را یک پیشامد ساده می گوییم.

هرگاه حداقل دو پیشامد ساده از فضای نمونه احتمال نابرابر داشته باشند، در این صورت فضای نمونه را فضای نمونه ای با احتمال غیر هم شانس می گوییم.

در فضای نمونه ای متناهی با احتمال غیرهمشانس اگر $S=\{s_{1},s_{2},…,s_{n}\}$ فضای نمونه ای و $A=\{a_{1},a_{2},…,a_{k}\}$ یک زیرمجموعه $k$ عضوی $S$ باشد همواره داریم:

$0 \le P(A) \le 1 \,\,\,,\,\,\,P(S)=1$

$P(A)=P(a_{1})+P(a_{2})+…+P(a_{k})$

کاهش فضای نمونه

در حالتی که فضای احتمال هم شانس است شرطی کردن یک پیشامد (مثل $A$ ) نسبت به پیشامد $B$ مثل این است که فضای نمونه یعنی $S$ را کنار گذاشته و $B$ را فضای نمونه تلقی کنیم. احتمال روی این فضای نمونه نیز هم شانس است به این رویکرد کاهش فضای نمونه می گویند.

احتمال شرطی چگونه محاسبه می شود؟

اگر با احتمال هم شانس سر و کار داشته باشیم محاسبه $P(A|B)$ ساده است کافی است تعداد حالات مطلوب را به تعداد حالات ممکن تقسیم کنیم ولی باید توجه داشته باشیم که چون می دانیم $B$ رخ داده دیگر همه ی اعضای پیشامد $A$ ممکن نیستند و لذا مجموعه ی حالات مطلوب در این وضعیت $A \cap B$ می باشد. در صورتی که $B$ پیشامدی باشد که $P(B) > 0$ ، برای هر پیشامد $A$ ، احتمال $A$ به شرط رخ دادن $B$ به شکل زیر تعریف می شود:

$P(A|B)=\frac{n(A \cap B)}{n(B)}$

توجه : شرط محاسبه احتمال پیشامد $A$ به شرط وقوع پیشامد $B$ آن است که $P(B)\neq 0$ . در غیر اینصورت $P(A|B)$ قابل تعریف نیست.

نکته : فرض کنید $B$ پیشامدی با احتمال مثبت باشد. داریم:

*اگر $A_{1}$ و $A_{2}$ دو پیشامد ناسازگار باشند داریم :

$P((A_{1}\cup A_{2})|B)=P(A_{1}|B)+P(A_{2}|B)$

*برای هر پیشامد $A$ داریم:

$P(A^{'}|B)=1-P(A|B)$

نکته : اگر $P(A|B)=P(A)$ باشد داریم $P(B|A)=P(B)$ . این تعاریف نیز مستقل بودن $A$ و $B$ را نشان می دهند.

نکته:

$P(A\cup B)=P(A)+P(B)-P(A\cap B)$

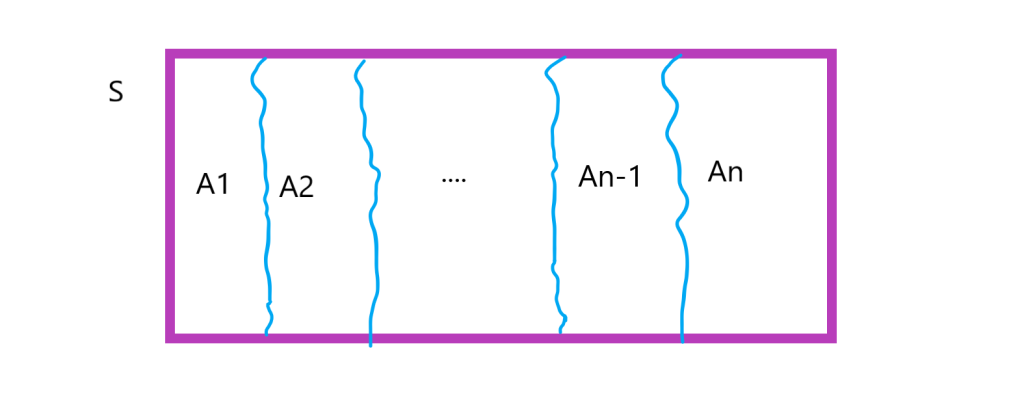
افراز یک مجموعه به زیر مجموعه های ناتهی چگونه انجام می شود؟

فرض کنیم $A_{1}$ و $A_{2}$ و $…$ و $A_{n}$ زیرمجموعه هایی ناتهی از مجموعه $S$ باشند، به گونه ای که اجتماع همه آنها برابر $S$ ، و اشتراک هر دو تای آنها تهی باشد، در این صورت می گوییم این مجموعه ها یک افراز روی $S$ درست کرده اند. به عبارتی داریم:

$A_{1} \cup A_{2} \cup …\cup A_{n}=S$

$A_{1}\cap A_{2}=\phi \,,…,A_{n-1} \cap A_{n}=\phi$

قانون احتمال کل چه می گوید؟

فرض کنید $B_{1},B_{2},…,B_{n}$ پیشامدهایی با احتمال ناصفر باشند که فضای نمونه را افراز می کنند. در این صورت برای هر پیشامد دلخواه $A$ داریم:

$P(A)=$

$P(B_{1})P(A|B_{1})+…+P(B_{n})P(A|B_{n})$

$=\sum_{k=1}^{n}P(B_{k})P(A|B_{k})$

ساده ترین شکل قانون احتمال کل برای $n=2$ به شکل زیر بیان می شود.

فرض کنید $B$ پیشامدی باشد که $0 < P(B) < 1$ . در این صورت برای هر پیشامد دلخواه $A$ داریم :

$P(A)=P(B)P(A|B)+P(B^{'})P(A|B^{'})$

حال اگر فرض کنیم $A_{1}$ و $A_{2}$ و $…$ و $A_{n}$ پیشامدهایی باشند که بر روی فضای نمونه ای $S$ یک افراز تشکیل داده باشند و $B$ یک پیشامد دلخواه باشد ، رابطه زیر حاصل خواهد شد که به آن قانون احتمال کل می گوییم:

$P(B)=\sum_{i=1}^{n}P(B\cap A_{i})$

$=\sum_{i=1}^{n}P(A_{i})P(B|A_{i})$

قانون ضرب احتمال

اگر $A$ و $B$ دو پیشامد باشند که $P(A) > 0$ آنگاه:

$P(A \cap B)=P(A)P(B|A)$

از این قانون معمولا وقتی استفاده می شود که بخواهیم عبارت سمت چپ تساوی را حساب کنیم.

قانون ضرب احتمال را می توان برای سه احتمال نوشت.

اگر $A_{1}$ و $A_{2}$ و $A_{3}$ پیشامدهایی با احتمال ناصفر باشند آنگاه :

$P(A_{1}\cap A_{2} \cap A_{3})=$

$P(A_{1})P(A_{2}|A_{1})P(A_{3}|(A_{1}\cap A_{2}))$

قانون بیز

فرض کنید $B_{1},B_{2},…,B_{n}$ پیشامدهایی با احتمال ناصفر باشند که فضای نمونه را افراز می کنند. در این صورت برای هر پیشامد دلخواه $A$ و هر $i \le n$ داریم:

$P(B_{i}|A)=\frac{P(B_{i})P(A|B_{i})}{P(A)}$

ساده ترین شکل قانون احتمال کل برای $n=2$ به شکل زیر بیان می شود.

فرض کنید $B$ پیشامدی باشد که $0 < P(B) < 1$ . در این صورت برای هر پیشامد دلخواه $A$ داریم :

$P(B|A)=\frac{P(B)P(A|B)}{P(A)}=$

$\frac{P(B)P(A|B)}{P(B)P(A|B)+P(B^{'})P(A|B^{'})}$

جمع بندی

در این مقاله احتمال تعریف شده. پیشامدهای ناسازگار و مستقل را تعریف کردیم. اصول احتمال، قانون احتمال کل، قانون ضرب احتمال و قانون بیز آموزش داده شده. افراز یک مجموعه به چند زیرمجموعه و ترجمه زبان گزاره ها به زبان مجموعه ها به عنوان پیش نیاز از فصل مجموعه و گزاره ی ریاضی بیان شده و در آخر با انتخاب های با جایگذاری و بدون جای گذاری مقاله را به پایان رساندیم. اگر علاقمند به مطالعه در مورد گزاره ها، مجموعه ها ، ترکیبیات و آمار هستید لطفا به مقاله هرکدام مراجعه کنید. لطفا نظرات خود را در مورد مقاله احتمال در قسمت کامنت ها بیان کنید.

جامع ترین آموزش درمورد احتمال هر آنچه که لازم است درباره ی احتمال بدانید

احتمال را تعریف کنید

احتمال رخداد یک پیشامد (اندازه گیری شانس در احتمالات هم شانس)

پیشامدهای تصادفی و برخی اعمال روی آنها

چه زمانی دو پیشامد ناسازگارند؟

چه زمانی دو پیشامد، مستقل اند؟

ترجمه زبان گزاره ها به زبان مجموعه ها

تشخیص فضای نمونه

اصول احتمال چیست؟

احتمال غیر هم شانس

کاهش فضای نمونه

احتمال شرطی چگونه محاسبه می شود؟

افراز یک مجموعه به زیر مجموعه های ناتهی چگونه انجام می شود؟

قانون احتمال کل چه می گوید؟

قانون ضرب احتمال

قانون بیز

دیدگاهتان را بنویسید لغو پاسخ

آخرین مطالب وبلاگ

دنباله های عددی

تابع خطی و معادله خط

تابع و دامنه و برد آن

تعیین علامت

عبارت و معادله گویا

معادله درجه دوم

معادله

عبارت جبری

قدرمطلق

دوره ها

دسترسی سریع

دسترسی سریع

مقالات مادر