همه چیز درباره ی مجموعه ها

مجموعه ها می توانند یک دسته از اعداد را نشان دهند. در این مقاله به بیان تعریف مجموعه ها می پردازیم. نحوه عضویت و زیرمجموعه مجموعه ها را بیان کردیم. به تعریف اجتماع و اشتراک و متمم و تفاضل مجموعه ها پرداختیم. به بیان ضرب دکارتی مجموعه ها، جبر مجموعه ها و قوانین جذب و دمورگان پرداختیم. همچنین در این مقاله می توانید در مورد بازه های اعداد بخوانید. افراز مجموعه ها در این مقاله آموزش داده شده است که در همنهشتی و عاد کردن اعداد صحیح مورد نیاز است.

مجموعه چیست؟

از مجموعه در ریاضی برای بیان و نمایش دسته ای از اشیای مشخص (عضویت این اشیا در مجموعه کاملا معین باشد) و متمایز (غیرتکراری) استفاده می شود.

اگر یک سری عدد را درون دو آکلاد قرار دهیم و آن را با حروف بزرگ انگلیسی نام گذاری کنیم در این صورت یک مجموعه تشکیل داده ایم.

در نوشتن مجموعه ها، ترتیب نوشتن عضوهای مجموعه، مهم نیست و با جابجایی عضوهای یک مجموعه، مجموعه جدیدی ساخته نمی شود؛ همچنین با تکرار عضوهای یک مجموعه، مجموعه جدیدی ساخته نمی شود.

اعضای مجموعه را چطور نشان دهیم؟

اگر مجموعه $A={a,b}$ را داشته باشیم برای نشان دادن اینکه $a$ عضوی از مجموعه $A$ است، می نویسیم $a \in A$ و می خوانیم $a$ عضو $A$ است. و چون $c$ عضو $A$ نیست می نویسیم $c \notin A$ و می خوانیم $c$ عضو $A$ نیست.

چطور مجموعه ها را را با نمودار ون نمایش دهیم؟

مجموعه را می توان با استفاده از منحنی ها یا خط های شکسته بسته نمایش داد. به این نوع نمایش (اینکه اعضای مجموعه را درون یک منحنی بسته قرار دهیم) نمایش نمودار وِن می نامند.

مجموعه متناهی و نامتناهی چه تفاوتی با هم دارند؟

مجموعه هایی که تعداد اعضای آنها یک عدد حسابی است، مجموعه های متناهی می نامیم.

به مجموعه هایی که نتوان تعداد اعضای آن را با یک عدد حسابی بیان کرد مجموعه نامتناهی می گویند. در واقع تعداد اعضای این مجموعه از هر عددی که در نظر بگیریم، بزرگتر است.

مجموعه تهی به چه مجموعه ای می گویند؟

اگر در مجموعه ای عضوی وجود نداشته باشد، آن را مجموعه تهی می نامیم و با نماد $\phi$ یا $\{\}$ نمایش می دهیم.

توجه: مجموعه های $\{\phi\}$ و $\{0\}$ هر کدام یک عضو دارند و تهی نیستند.

چه زمانی دو مجموعه برابرند؟

اگر عضوهای دو مجموعه $A$ و $B$ یکسان باشند و هر عضو $A$ ، عضوی از $B$ و هر عضو $B$ عضوی از $A$ باشد در این صورت دو مجموعه $A$ و $B$ برابرند و می نویسیم $A=B$ .

چه زمانی یک مجموعه زیرمجموعه دیگری است؟

اگر همه ی عضوهای مجموعه $B$ در مجموعه $A$ قرار داشته باشد می گوییم مجموعه $B$ زیرمجموعه ی مجموعه $A$ است. می نویسیم $B\subseteq A$ .

هر مجموعه زیر مجموعه خودش است مثلا $A \subseteq A$ .

اگر بتوانیم عضوی در $B$ بیابیم که در $A$ نباشد، می گوییم $B$ زیرمجموعه $A$ نیست و می نویسیم $B \not\subseteq A$ .

مجموعه تهی زیرمجموعه هر مجموعه ای دلخواه مانند $A$ است؛ یعنی $\phi \subseteq A$ .

تعداد زیرمجموعه های یک مجموعه را چطور بدست آوریم؟

اگر $A$ یک مجموعه $n$ عضوی باشد، تعداد زیرمجموعه های $A$ برابر با $2^{n}$ است.

مجموعه ی همه ی زیرمجموعه های $A$ ، مجموعه توانی $A$ نامیده می شود و آن را با $P(A)$ نمایش می دهیم. اگر $A$ یک مجموعه $n$ عضوی باشد، $P(A)=2^{n}$ است.

اگر $A$ ، $n$ عضو داشته باشد، در این صورت $P(A)$ ، $2^{n}$ عضو دارد.

اگر $A \subseteq B$ به طوری که $A \neq B$ آنگاه $A$ زیرمجموعه ی محض یا سره ی $B$ نامیده می شود.

تعریف زیرمجموعه به کمک نمادهای ریاضی

فرض کنید $A$ و $B$ دو مجموعه باشند به طوری که هر عضو $A$ ، عضوی از $B$ باشد، در این صورت $A$ را زیرمجموعه ی $B$ نامیده و می نویسند $A \subseteq B$ .

اگر عضوی در $A$ وجود داشته باشد، به طوری که آن عضو در مجموعه ی $B$ نباشد، در این صورت $A$ زیرمجموعه $B$ نیست و می نویسند $A \not\subseteq B$ . با استفاده از نمادهای ریاضی می توان تعریف های $A \subseteq B$ و $A\not\subseteq B$ را به صورت زیر نوشت:

$A \subseteq B \,\,\, \Leftrightarrow \,\,\,\forall x ; (x \in A \,\,\Rightarrow \,\, x \in B)$

$A \not\subseteq B \,\,\, \Leftrightarrow \,\,\,\exists x ; (x \in A \,\,\land \,\, x \notin B)$

روش عضوگیری دلخواه برای اثبات اینکه یک زیرمجموعه مجموعه دیگر است.

هرگاه بخواهیم ثابت کنیم $A \subseteq B$ و اعضای مجموعه های $A$ و $B$ در دسترس نباشند، کافی است عضوی دلخواه مانند $x$ از $A$ فرض کنیم، سپس با استفاده از فرض های داده شده نشان دهیم که $x$ در $B$ وجود دارد. از آنجا که $x$ دلخواه بوده است در واقع هر عضو $A$ در $B$ وجود دارد. بنابراین با توجه به تعریف زیرمجموعه ثابت کردیم $A \subseteq B$ .

در ادامه چند ویژگی مهم در مجموعه ها که با روش عضو گیری قابل اثبات است بیان شده است.

ویژگی 1: فرض کنید $A$ و $B$ و $C$ سه مجموعه با مرجع $U$ باشند، به طوری که $A \subseteq B$ و $B \subseteq C$ داریم: $A \subseteq C$

ویژگی 2: فرض کنید $A$ و $B$ دو مجموعه با مرجع $U$ باشند و $A \subseteq B$ . ثابت کنید $B^{'} \subseteq A^{'}$ .

ویژگی 3: برای هر مجموعه دلخواه مانند $A$ با مجموعه مرجع $U$ داریم: $\phi \subseteq A$

ویژگی 4: فرض کنید $A$ و $B$ دو مجموعه با مرجع $U$ باشند داریم $A \subseteq A \cup B$ .

ویژگی 5: فرض کنید $A$ و $B$ و $C$ و $D$ جهار مجموعه با مرجع $U$ باشند، به طوری که $A \subseteq B$ و $C \subseteq D$ داریم:

$A \cap C \subseteq B \cap D \,\,\,,\,\,\,A\cap C \subseteq B \cup D \,\,\,,\,\,\,A \cup C \subseteq B \cup D$

ویژگی 6: فرض کنید $A$ و $B$ و $C$ سه مجموعه با مرجع $U$ باشند، به طوری که $A \subseteq C$ و $B \subseteq C$ داریم:

$A \cup B \subseteq C$

مجموعه های متناهی و نامتناهی چه تفاوتی با هم دارند؟

به مجموعه هایی که بتوان تعداد اعضای آن را مشخص کرد هر چند تعداد اعضا زیاد باشد مجموعه متناهی می گویند. مثل مجموعه درخت های کره زمین. اما اگر نتوان تعداد اعضای یک مجموعه را نتوان مشخص کرد به آن مجموعه نامتناهی می گویند. مثل مجموعه اعداد بزرگتر از 100 .

نمایش مجموعه های اعداد به کمک علائم ریاضی

مجموعه اعداد طبیعی را با $\Bbb{N}$ نمایش می دهیم و آن را به صورت $\Bbb{N}=\{1,2,3,…\}$ می نویسیم.

نمایش اعداد طبیعی زوج : مجموعه اعداد زوج را با $\Bbb{E}$ نشان می دهند. اعضای این مجموعه خاصیت مشترکی دارند آنها همگی مضرب 2 هستند. در نتیجه می توان مجموعه اعداد طبیعی زوج را به صورت $\Bbb{E}=\{2k |k \in \Bbb{N}\}$ نمایش داد. می خوانیم $\Bbb{E}$ برابر است با مجموعه اعدادی به شکل $2k$ به طوری که $k$ متعلق ( $\in$ ) به مجموعه اعداد طبیعی ( $\Bbb{N}$ ) باشد.

نمایش اعداد طبیعی فرد: مجموعه اعداد فرد را با $\Bbb{O}$ نشان می دهند. اعضای این مجموعه خاصیت مشترکی دارند آنها همگی باقیمانده یک در تقسیم بر 2 دارند. در نتیجه می توان مجموعه اعداد طبیعی فرد را به صورت $\Bbb{O}=\{2k-1 |k \in \Bbb{N}\}$ نمایش داد. می خوانیم $\Bbb{O}$ برابر است با مجموعه اعدادی به شکل $2k-1$ به طوری که $k$ متعلق ( $\in$ ) به مجموعه اعداد طبیعی ( $\Bbb{N}$ ) باشد.

نمایش مضارب طبیعی عدد 3: اعضای این مجموعه خاصیت مشترکی دارند آنها همگی مضرب 3 هستند. در نتیجه می توان مجموعه مضارب عدد سه را به صورت $\{3k |k \in \Bbb{N}\}$ نمایش داد.

مجموعه اعداد حسابی را با $\Bbb{W}$ نشان می دهیم و اعضای آن به صورت

$\Bbb{W}=\{0,1,2,3,…\}$ است.

مجموعه اعداد حسابی را می توان با نمادهای ریاضی به صورت $\Bbb{W}=\{k-1 |k \in \Bbb{N}\}$ نوشت. هر عدد طبیعی یک عدد حسابی است یعنی مجموعه اعداد طبیعی زیرمجموعه اعداد حسابی است پس داریم: $\Bbb{N} \subseteq \Bbb{W}$ .

مجموعه اعداد صحیح را با $\Bbb{Z}$ نشان می دهیم و اعضای آن به صورت $\Bbb{Z}=\{…,-3,-2,-1,0,1,2,3,…\}$ است.

مجموعه اعداد صحیح را می توان با نمادهای ریاضی به صورت $\Bbb{Z}=\{\pm k |k \in \Bbb{W}\}$ نوشت. هر عدد طبیعی و هر عدد حسابی یک عدد صحیح است. یعنی مجموعه اعداد طبیعی زیرمجموعه اعداد صحیح است پس داریم: : $\Bbb{N} \subseteq \Bbb{Z}$ .

همه ی اعداد طبیعی و حسابی، عدد صحیح هم هستند پس: $\Bbb{N} \subseteq \Bbb{W}\subseteq \Bbb{Z}$

مجموعه اعداد گویا را با $\Bbb{Q}$ نمایش می دهند چون اولین عدد گویای بزرگتر از هر عدد گویا مشخص نیست، نمی توان این مجموعه را با عضوها مشخص کرد؛ به همین دلیل مجموعه اعداد گویا را با نمادهای ریاضی تعریف می کنیم:

$\Bbb{Q}=\{\frac{a}{b} | a,b \in \Bbb{Z} , b \neq 0\}$

مجموعه اعداد گنگ را به صورت $\Bbb{Q}^{'}$ یا $\Bbb{Q}^{c}$ نشان می دهیم هر عدد حقیقی که گویا نباشد گنگ محسوب می شود.

مجموعه اعداد حقیقی اجتماع اعداد گویا و گنگ است $\Bbb{Q}^{'} \cup \Bbb{Q}=\Bbb{R}$

$\Bbb{N}\subseteq \Bbb{W}\subseteq \Bbb{Z} \subseteq \Bbb{Q} \subseteq \Bbb{R}$

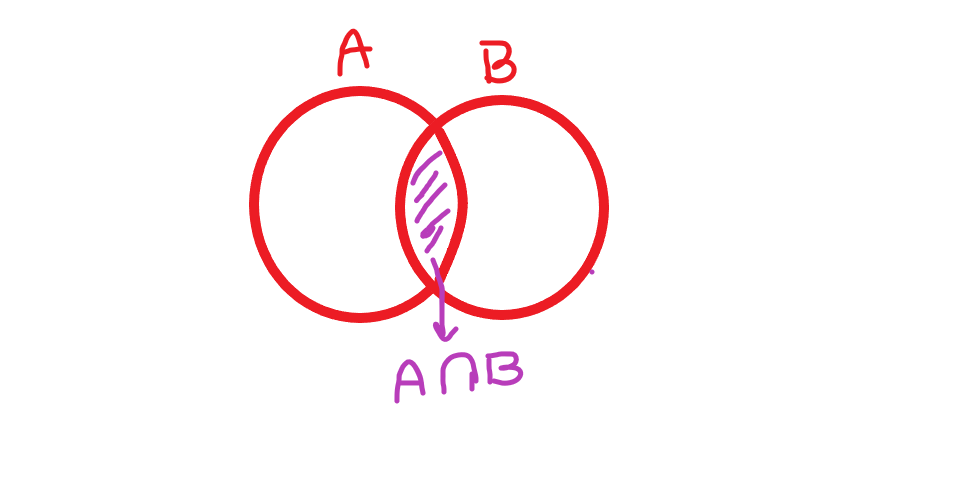
اشتراک دو مجموعه را چطور بدست آوریم؟

اشتراک دو مجموعه $A$ و $B$ ، مجموعه ای شامل همه عضوهایی است که هم عضو $A$ و هم عضو $B$ هستند. این مجموعه را با نماد $A \cap B$ نشان می دهیم. در نمودار وِن زیر قسمت هاشور خورده اشتراک دو مجموعه را نشان می دهد. اشتراک دو مجموعه را با نماد ریاضی به صورت زیر نشان می دهیم.

$A \cap B=\{x | x \in A \land x \in B \}$

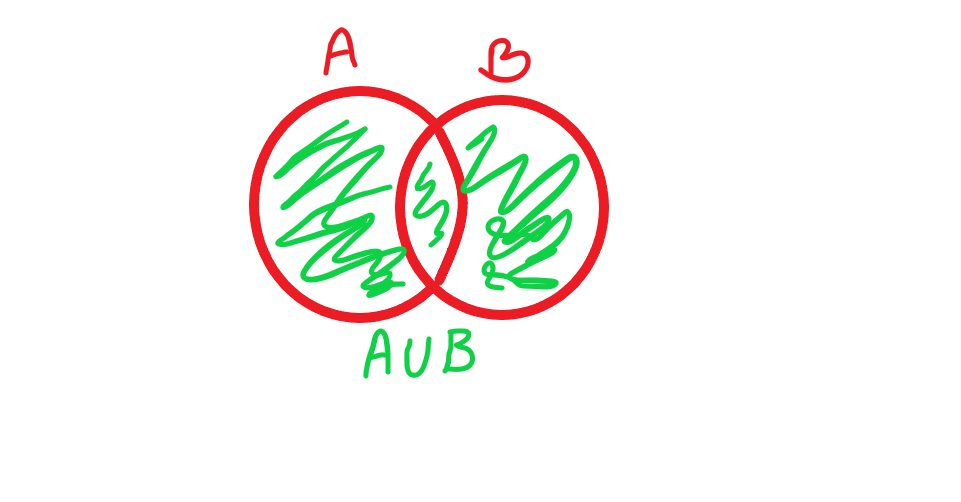
اجتماع دو مجموعه را چطور بدست می آوریم؟

اجتماع دو مجموعه $A$ و $B$ ، مجموعه ای شامل همه عضوهایی است که حداقل در یکی از دو مجموعه $A$ و $B$ باشند. این مجموعه را با نماد $A \cup B$ نشان می دهیم. در نمودار وِن زیر قسمت هاشور خورده اجتماع دو مجموعه را نشان می دهد. اجتماع دو مجموعه را با نماد ریاضی به صورت زیر نشان می دهیم.

$A \cup B=\{x | x \in A \lor x \in B \}$

تعداد عضوهای اجتماع دو مجموعه

به هر دو مجموعه مثل $A$ و $B$ که فاقد عضو مشترک باشند، دو مجموعه جدا از هم یا مجزا می گوییم $A \cap B=\phi$

اگر $A$ و $B$ دو مجموعه متناهی دلخواه باشند داریم:

$n(A \cup B)=n(A)+n(B)-n(A \cap B)$

در سوالات اگر بین دو مجموعه از کلمه ربط “یا” استفاده شده یعنی اجتماع آن دو مجموعه و اگر از کلمه ربط “و” استفاده شده یعنی اشتراک دو مجموعه .

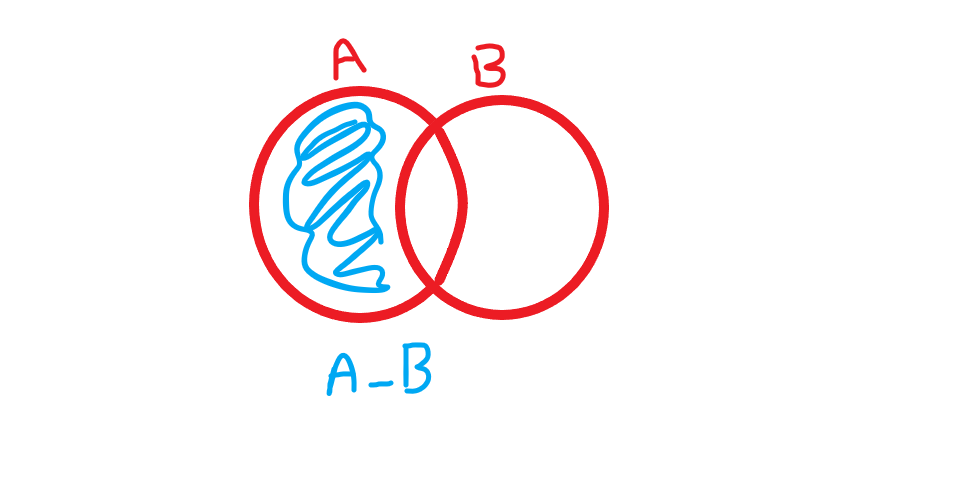
تفاضل دو مجموعه را چطور بدست آوریم؟

مجموعه $A-B$ ( $A$ منهای $B$ )، مجموعه ای است شامل همه عضوهایی است که عضو مجموعه $A$ هستند ولی عضو مجموعه $B$ نیستند. این مجموعه را با نماد $A-B$ نشان می دهیم. در نمودار وِن روبرو قسمت هاشور خورده تفاضل دو مجموعه را نشان می دهد.

$A-B=\{x | x \in A \land x \notin B\}$

قرارداد: تعداد عضوهای هر مجموعه مانند $A$ را با $n(A)$ نمایش می دهیم به عنوان مثال اگر $A$ مجموعه ای $k$ عضوی باشد، می نویسیم $n(A)=k$

نکات:

اشتراک دو مجموعه زیرمجموعه اجتماع همان دو مجموعه است.

هر یک از دو مجموعه $A$ و $B$ زیرمجموعه $A \cup B$ است.

اشتراک دو مجموعه $A$ و $B$ زیرمجموعه ی هر یک از دو مجموعه $A$ و $B$ است.

اجتماع دو مجموعه $(B-A)$ و $(A\cap B)$ با مجموعه $B$ مساوی است.

متمم یک مجموعه

در هر مبحث، مجموعه ای را که همه مجموعه های مورد بحث، زیرمجموعه آن باشند، مجموعه مرجع می نامیم و آن را با $U$ نشان می دهیم.

هرگاه $U$ مجموعه مرجع باشد $U \subseteq A$ ، آنگاه مجموعه $A-U$ را متمم $A$ می نامیم و آن را با نماد $A^{'}$ نشان می دهیم. به عبارت دیگر $A^{'}$ شامل عضوهایی از $U$ است که در $A$ نیستند.

چطور یک مجموعه را به چند زیرمجموعه افراز کنیم؟

فرض می کنیم $A \neq \phi$ یک مجموعه و $A_{1},A_{2},…,A_{n}$ زیرمجموعه های $A$ باشند. مجموعه ی $A$ به $n$ زیرمجموعه $A_{1},A_{2},…,A_{n}$ افراز شده است، هرگاه سه شرط زیر برقرار باشد.

$\forall_{1 \le i \le n} ; A_{i} \neq \phi$

$\forall_{i,j(i \neq j)} ; A_{i} \cap A_{j}=\phi$

$A_{1} \cup A_{2} \cup …\cup A_{n}=\cup_{i=1}^{n} A_{i}=A$

در نتیجه در بین زیرمجموعه های مجموعه فرضی $A$ زیرمجموعه هایی یافت می شوند که سه ویژگی دارند

اول : هیچ کدام تهی نیستند

دوم : دو به دو جدا از هم هستند

سوم : اجتماع آنها برابر $A$ می شود.

به آنها افراز های مجموعه $A$ می گویند.

جبر مجموعه ها

برای هر دو مجموعه دلخواه $A$ و $B$ از مجموعه ی مرجع $U$ داریم:

$A \cap B=B \cap A\,\,\,\,,\,\,\,\, A\cup B=B \cup A$

برای هر سه مجموعه دلخواه $A$ و $B$ و $C$ از مجموعه ی مرجع $U$ داریم:

$A\cap (B \cap C)=(A \cap B)\cap C$

$A \cup (B \cup C)=(A\cup B)\cup C$

برای هر سه مجموعه دلخواه $A$ و $B$ و $C$ از مجموعه ی مرجع $U$ اجتماع نسبت به اشتراک خاصیت توزیع پذیری دارد. داریم:

$A\cup (B \cap B)=(A \cup B)\cap ( A \cup C)$

تذکر

$A \cup A^{'}=U \,\,,\,\,A\cap A^{'}=\phi$

$A \cup U=U\,\,,\,\,A\cap U=A$

برای هر دو مجموعه دلخواه $A$ و $B$ از مجموعه ی مرجع $U$ داریم

$A \subseteq B \,\,\, \Leftrightarrow \,\,\,A \cap B=A$

$A \subseteq B \Leftrightarrow \,\,\,A \cup B=B$

قانون جذب یا همپوشانی مجموعه ها

برای هر دو مجموعه دلخواه $A$ و $B$ از مجموعه ی مرجع $U$ داریم:

$A \cap (A \cup B)=A$

$A \cup (A \cap B)=A$

قانون دمورگان مجموعه ها

برای هر دو مجموعه دلخواه از مجموعه مرجع $U$ داریم:

$(A \cap B)^{'}=(A^{'} \cup B^{'})$

$(A \cup B )^{'}=(A^{'}\cap B^{'})$

چه موقع دو مجموعه با هم برابرند؟

فرض کنیم $A$ و $B$ دو مجموعه با مرجع $U$ باشند، به طوری که هر عضو $A$ ، عضوی از $B$ و هر عضو $B$ عضوی از $A$ باشد؛ یعنی $A \subseteq B$ و $B \subseteq A$ در این صورت $A$ با $B$ مساوی است و می نویسیم $A=B$ به عبارت دیگر تساوی دو مجموعه را می توان به صورت زیر نوشت.

$A=B \,\, \Leftrightarrow \,\,[(A \subseteq B ) \land ( B \subseteq A)]$

فرض کنید $A$ و $B$ دو مجموعه با مرجع $U$ باشند، داریم:

$A\cap B=B \cap A$

فرض کنید $A$ و $B$ دو مجموعه با مرجع $U$ باشند، و $A \subseteq B$ آنگاه داریم:

$A-B=\phi$

فرض کنید $A \subseteq \phi$ داریم $A=\phi$

فرض کنید $U \subseteq A$ داریم $A=U$

فرض کنید $A$ و $B$ دو مجموعه با مرجع $U$ باشند و $A\cap B=\phi$ در اینصورت داریم:

$B-A=B \,\,\,\,,\,\,\,\,B \subseteq A^{'}$

ضرب دکارتی دو مجموعه

هر دو شیئی مانند $x$ و $y$ ، تشکیل یک زوج می دهند که اگر برای آنها ترتیب قائل باشیم، به آن یک زوج مرتب گفته می شود و با نماد $(x,y)$ نشان می دهیم . می دانیم $(x,y)=(z,t)$ اگر و تنها اگر $x=z$ و $y=t$ (در مقاله تابع چیزهای بیشتری درباره ی زوج های مرتب می آموزید)

عمل ضرب دکارتی بین دو مجموعه $A$ و $B$ این امکان را برای ما فراهم می سازد تا مجموعه جدیدی بسازیم که اعضای آن هر کدام یک زوج مرتب باشند و هر یک از این زوجهای مرتب از اعضای $A$ و $B$ ساخته می شوند. بنابراین، مجموعه حاصل دارای اعضایی از جنس زوج مرتب بوده و به اعضای $A$ یا $B$ شبیه نبوده و فقط اعضای $A$ و $B$ در ساختن آنها نقش دارند.

تعریف ضرب دکارتی بین دو مجموعه: اگر $A$ و $B$ دو مجموعه دلخواه باشند $A \times B$ مجموعه ای است که بصورت زیر تعریف می شود:

$A \times B =\{(x,y) |x \in A \land y \in B \}$

هر $(x,y)$ متعلق $A \times B$ همواره مولفه اول یعنی $x$ باید از مجموعه $A$ و متناظر با مولفه دوم یعنی $y$ باید از مجموعه $B$ باشد.

اگر $n(A)=m$ و $n(B)=k$ با استفاده از تعریف عمل ضرب دکارتی و حاصل ضرب داریم:

$n(A \times B)=m\times k$

در حالت کلی

$A \times B \neq B \times A$

اگر $A$ و $B$ دو مجموعه دلخواه باشند در این صورت

$A \times \phi = \phi \times A= \phi$

$A \times B =B \times A \,\,\,\Rightarrow \,\,\, A= \phi \lor B =\phi \lor A=B$

همه ی فرمول های مربوط به مجموعه را می توانید در جدول زیر ببینید:

جمع بندی

در این مقاله به تعریف مجموعه ها و نحوه نمایش مجموعه ها با نمودار ون و علائم ریاضی پرداختیم. همچنین به تعریف اجتماع، اشتراک، تفاضل و متمم مجموعه ها پرداختیم. بازه های اعداد را آموزش دادیم. جبر مجموعه ها و ضرب دکارتی مجموعه ها و قوانین دمورگان و قوانین جذب را آموزش دادیم. اگر علاقمند به آموزش در حوزه آمار، ترکیبیات و احتمال هستید به مقالات مربوطه مراجعه کنید. لطفا نظرات خود را در مورد مقاله مجموعه در قسمت کامنت ها بیان کنید.

همه چیز درباره ی مجموعه ها

مجموعه چیست؟

اعضای مجموعه را چطور نشان دهیم؟

چطور مجموعه ها را را با نمودار ون نمایش دهیم؟

مجموعه متناهی و نامتناهی چه تفاوتی با هم دارند؟

مجموعه تهی به چه مجموعه ای می گویند؟

چه زمانی دو مجموعه برابرند؟

چه زمانی یک مجموعه زیرمجموعه دیگری است؟

تعداد زیرمجموعه های یک مجموعه را چطور بدست آوریم؟

تعریف زیرمجموعه به کمک نمادهای ریاضی

روش عضوگیری دلخواه برای اثبات اینکه یک زیرمجموعه مجموعه دیگر است.

مجموعه های متناهی و نامتناهی چه تفاوتی با هم دارند؟

نمایش مجموعه های اعداد به کمک علائم ریاضی

اشتراک دو مجموعه را چطور بدست آوریم؟

اجتماع دو مجموعه را چطور بدست می آوریم؟

تعداد عضوهای اجتماع دو مجموعه

تفاضل دو مجموعه را چطور بدست آوریم؟

متمم یک مجموعه

چطور یک مجموعه را به چند زیرمجموعه افراز کنیم؟

جبر مجموعه ها

چه موقع دو مجموعه با هم برابرند؟

ضرب دکارتی دو مجموعه

دیدگاهتان را بنویسید لغو پاسخ

آخرین مطالب وبلاگ

دنباله های عددی

تابع خطی و معادله خط

تابع و دامنه و برد آن

تعیین علامت

عبارت و معادله گویا

معادله درجه دوم

معادله

عبارت جبری

قدرمطلق

دوره ها

دسترسی سریع

دسترسی سریع

مقالات مادر