هر آنچه که باید درباره ی شاخص های مرکزی میانگین میانه چارک ها و مد بدانید

شاخص های مرکزی شامل میانگین میانه چارک اول چارک دوم یا میانه چارک سوم و مد شاخص هایی از جنس آمار توصیفی هستند که می توانند داده های آماری را در یک نگاه توصیف کنند. در این مقاله به بیان تعریف هر کدام از آنها پرداختیم و برای هر کدام فرمول ها و گام هایی برای محاسبه شان معرفی کردیم و با ذکر مثال آموزش هر کدام از شاخص های مرکزی را کامل کردیم. پیشنهاد می کنیم قبل از خواندن این مقاله با برخی از اصطلاحات آماری در مقاله ی مربوطه آشنا شوید و همچنین بعد از خواندن این مقاله حتما به سراغ مقاله های شاخص های پراکندگی و جدول فراوانی و نمودارهای آماری بروید تا علم خود را درباره ی آمار کامل کنید.

شاخص مرکزی میانگین چیست و چگونه بدست می آید؟

برای بدست آوردن میانگین داده ها همه ی آنها را با هم جمع می کنیم و بر تعدادشان تقسیم می کنیم.

مجموع داده ها : اگر $n$ داده ی $x_{1},x_{2},…,x_{n}$ داشته باشیم ، مجموع آن داده ها را با نماد سیگما $\sum_{}^{}$ نمایش می دهیم و داریم:

$\sum_{i=1}^{n} x_{i}=x_{1}+x_{2}+…+x_{n}$

عبارت $\sum_{i=1}^{n} x_{i}$ را سیگمای $i$ از $1$ تا $n$ ، $x_{i}$ می خوانیم.

میانگین یا متوسط داده ها: اگر $n$ مشاهده بصورت $x_{1},x_{2},…,x_{n}$ داشته باشیم میانگین آنها را با نماد $\overline{x}$ نشان می دهیم و بصورت زیر تعریف می شود:

$\overline{x}=\frac{\sum_{i=1}^{n} x_{i}}{n}=\frac{x_{1}+x_{2}+…+x_{n}}{n}$

چه نکاتی درباره میانگین باید بدانیم؟

*میانگین مرسوم ترین و باثبات ترین شاخص گرایش به مرکز است. بهترین برآورد از جامعه ، میانگین است.
*میانگین شاخص فاصله ای است و برای داده هایی با مقیاس فاصله ای یا نسبتی تعریف شده است.
*در محاسبه میانگین از همه ی اعداد یا داده ها استفاده می شود و داده های خیلی بزرگ یا خیلی کوچک در میانگین تاثیر دارد.
*مجموع انحراف از میانگین همیشه صفر است.
*اگر داده پرت ( داده ای که با سایر داده ها اختلاف زیادی داشته باشد یعنی خیلی بزرگتر یا خیلی کوچکتر از آنها باشد) داشته باشیم میانگین شاخص مرکزی مناسبی برای این داده ها نیست چرا که داده پرت را هم در محاسبات در نظر می گیرد.

اگر داده ها دسته بندی شده بودند چطور میانگین داده ها را بدست آوریم؟ (میانگین موزون)

اگر تعداد داده ها زیاد باشد و داده ها دسته بندی شده باشند می توان مرکز هر دسته را در تعداد دسته ضرب کرد و بعد حاصل را بر تعداد کل داده ها تقسیم کرد تا میانگین بدست آید.

اگر داده ی $x_{1}$ به تعداد $f_{1}$ وجود داشته باشد و داده ی $x_{2}$ به تعداد $f_{2}$ تکرار شده باشد و به همین ترتیب داده ی $x_{n}$ به تعداد $f_{n}$ وجود داشته باشد آنگاه میانگین داده ها بصورت $\overline{x}=\frac{f_{1}x_{1}+f_{2}x_{2}+…+f_{n}x_{n}}{n}$ به طور کلی میانگین موزون داده ها را به صورت زیر تعریف می کنیم:

میانگین موزون داده ها : اگر $n$ داده ی $x_{1},x_{2},…,x_{n}$ داشته باشیم به طوری که هر یک از این داده ها دارای تعداد تکرار $w_{1},w_{2},…,w_{n}$ باشند ( که به هر یک از $w_{i}$ ها وزن داده متناظر با آن می گوییم.) آنگاه میانگین موزون داده ها را که با نماد $\overline{x}_{w}$ نشان می دهیم به صورت زیر بدست می آید:

$\overline{x}_{w}=\frac{\sum_{i=1}^{n} w_{i}x_{i}}{\sum_{i=1}^{n} w_{i}}=\frac{w_{1}x_{1}+w_{2}x_{2}+…+w_{n}x_{n}}{w_{1}+w_{2}+…+w_{n}}$

حل یک مثال برای کامل کردن آموزش میانگین

مثلا در داده های فرضی 5 و 5 و 8 و 8 و 8 و 11 و 11 می توان میانگین را به صورت زیر بدست آورد:

$\overline{x}=\frac{5+5+8+8+8+11+11}{7}$

$=\frac{56}{7}=8$

یا می توان با توجه به اینکه برخی داده ها تکرار می شوند از میانگین موزون آنها استفاده کرد:

$\overline{x}=\frac{2 \times 5+3\times 8+2\times 11}{7}$

$=\frac{56}{7}=8$

اگر طبق آنچه در جدول فراوانی خواندیم یک جدول به ما دادند و میانگین داده ها را خواستند باید مرکز هر دسته را بدست آوریم و آن را به عنوان نماینده هر دسته در نظر گرفته و فراوانی را برای آن در نظر بگیریم و سپس میانگین را برای داده ها حساب کنیم.

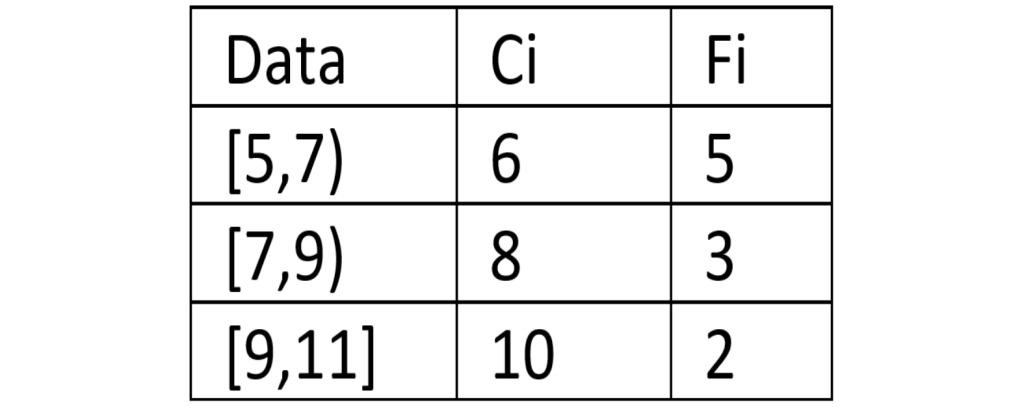
مثلا اگر بخواهیم میانگین داده هایی را که در مثال اخیر به ما دادند بدست آوریم داده ها را به صورت زیر دسته بندی کرده فراوانی هر دسته را در ستون $F_{i}$ می نویسیم و مرکز هر دسته را در ستون $C_{i}$ می نویسیم تا جدول زیر بدست آید: (برای اطلاعات بیشترد درباره جدول فراوانی به مقاله جدول فراوانی و نمودارهای آماری مراجعه کنید)

برای اینکه میانگین داده ها را بدست آوریم مرکز هر دسته را در فراوانی دسته ضرب می کنیم تا میانگین موزون را بدست آوریم:

$\overline{x}=\frac{2 \times 5+3\times 8+2 \times 11}{7}$

$=\frac{56}{7}=8$

می بینیم اگر به جای اینکه همه ی داده ها را در اختیار داشته باشیم (در مقاله ی جدول فراوانی و نمودارهای آماری گفتیم که چطور داده های فرضی که در مثال قبل گفته شد به جدول فراوانی بالا تبدیل کردیم) داده های دسته بندی شده را در اختیار داشته باشیم آنگاه میانگین در این دو حالت با اینکه الزاما با هم برابر نیست اما نزدیک بهم است.

شاخص مرکزی میانه چگونه بدست می آید؟

پس از مرتب کردن داده ها مقداری که تعداد داده های بعد از آن با تعداد داده های قبل از آن برابر است، میانه است. اگر تعداد داده ها فرد باشد داده وسط میانه است و اگر تعداد داده ها زوج باشد میانه برابر با میانگین دو داده ی وسطی است.

چه نکاتی را باید در مورد میانه بدانم؟

*اگر در داده ها داده ی دور افتاده داشتیم باید از میانه بعنوان یک شاخص مرکزی به جای میانگین استفاده کنیم. چون میانه تحت تاثیر ارزش تمام داده ها قرار ندارد.
*میانه یک شاخص ترتیبی است و میانه با مقیاس های ترتیبی فاصله ای و نسبتی به کار برده می شود.
*میانه به اغلب داده های توزیع نزدیک است.
*ثبات میانه از میانگین کمتر و از مد بیشتر است.

حل یک مثال برای کامل کردن آموزش میانه

مثلا در داده های فرضی 5 و 5 و 8 و 8 و 8 و 11 و 11 میانه به صورت زیر بدست می آید:

گام اول : همه داده ها را به ترتیب از کوچک به بزرگ مرتب می کنیم:

$5,5,8,8,8,11,11$

گام دوم: تعداد داده ها را می شماریم: در اینجا 7 داده داریم.

گام سوم: اگر تعداد داده ها فرد بود داده وسطی همان میانه است و اگر تعداد داده ها زوج بود میانه برابر با میانگین دو داده وسط است. داده وسط در بین هفت داده همان داده چهارم است که برابر با 8 است. بنابراین میانه برابر با 8 می باشد.

چارک ها چگونه بدست می آیند؟ چارک اول، چارک دوم، چارک سوم

وقتی میانه یک سری داده را بدست آوردیم داده ها به دو دسته تقسیم می شوند اگر میانه دسته ی اول که شامل داده های کوچکتر از میانه و نه خود ِ میانه می باشد را بدست آوریم در واقع چارک اول داده ها را بدست آوردیم. و اگر میانه دسته دوم که شامل داده های بزرگتر از میانه و نه خود ِ میانه می باشد را بدست آوریم در واقع چارک سوم داده ها را بدست آوردیم. میانه همان چارک دوم داده ها می باشد.

حل دو مثال برای کامل کردن آموزش چارک ها

مثال اول: مثلا در داده های فرضی 5 و 5 و 8 و 8 و 8 و 11 و 11 چارک ها به صورت زیر بدست می آید:

گام اول: همه داده ها را به ترتیب از کوچک به بزرگ مرتب می کنیم:

$5,5,8,8,8,11,11$

گام دوم: تعداد داده ها را می شماریم: در اینجا 7 داده داریم.

گام سوم: اگر تعداد داده ها فرد بود داده وسطی همان میانه است و اگر تعداد داده ها زوج بود میانه برابر با میانگین دو داده وسط است. داده وسط در بین 7 داده همان داده چهارم است. بنابراین میانه برابر با 8 می باشد.

گام چهارم: داده های کمتر از میانه را می نویسیم.

$5,5,8$

گام پنجم: میانه داده های گام چهارم که داده های کمتر از میانه هستند را بدست می آوریم. که میانه این داده ها برابر 5 است که می شود چارک اول داده های اصلی سوال.

گام ششم: داده های بیشتر از میانه را می نویسیم.

$8,11,11$

گام هفتم: میانه داده های گام ششم که داده های بیشتر از میانه هستند را بدست می آوریم. که میانه این داده ها برابر 11 است که می شود چارک سوم داده های اصلی سوال.

مثال دوم: مثلا در داده های فرضی 2 و 3 و 4 و 5 و 6 و 7 و 8 و 9 و 10 و 11 و 12 چارک ها به صورت زیر بدست می آید:

گام اول: همه داده ها را به ترتیب از کوچک به بزرگ مرتب می کنیم:

$2,3,4,5,6,7,8,9,10,11,12$

گام دوم: تعداد داده ها را می شماریم: در اینجا 11 داده داریم.

گام سوم: اگر تعداد داده ها فرد بود داده وسطی همان میانه است و اگر تعداد داده ها زوج بود میانه برابر با میانگین دو داده وسط است. داده وسط در بین 11 داده ، داده ششم است که همان 7 است. بنابراین میانه برابر با 7 می باشد.

گام چهارم: داده های کمتر از میانه را می نویسیم.

$2,3,4,5,6$

گام پنجم: میانه داده های گام چهارم که داده های کمتر از میانه هستند را بدست می آوریم. چون تعداد این داده ها 5 تا یعنی فرد است چارک اول برابر با داده سوم یعنی 4 است.

گام ششم: داده های بیشتر از میانه را می نویسیم.

$8,9,10,11,12$

گام هفتم: میانه داده های گام ششم که داده های بیشتر از میانه هستند را بدست می آوریم. چون تعداد این داده ها 5 تا یعنی فرد است چارک سوم برابر با داده سوم یعنی 10 است.

بنابراین چارک اول برابر با 4 و چارک دوم برابر با 7 و چارک سوم برابر با 10 می باشد.

به طور کلی عدد وسط مجموعه ای از داده ها را که از کوچک به بزرگ مرتب شده باشند میانه داده ها می گوییم و آن را با $Q_{2}$ نشان می دهیم میانه یک دوم اول داده های مرتب شده را چارک اول می گوییم و آن را با $Q_{1}$ نشان می دهیم همچنین میانه یک دوم آخر داده های مرتب شده را چارک سوم می گوییم و آن را با $Q_{3}$ نشان می دهیم.

مد چه نوع شاخص مرکزی ای می باشد؟

داده ای که بیشترین فراوانی را داشته باشد، مد یا نما داده ها نام دارد.

چه نکاتی را راجع به مد باید بدانم؟

*اگر در داده هایی، همه ی داده ها فراوانیِ یکسان (یا وزن یکسان) داشته باشند ، آن گاه این داده ها مد ندارند.

*در بعضی از توزیع ها بیشتر از یک مد وجود دارد. اگر در داده هایی ، دو داده بیشترین فراوانی را داشته باشند ، آن گاه این داده ها دو مد دارند.

*مد یک شاخص اسمی است و اغلب در وسط داده ها قرار دارد.

*مد برآورد خیلی ضعیفی از پارامتر جامعه است و به ندرت بکار برده می شود.

حل یک مثال برای کامل کردن آموزش مد

مثلا برای داده های فرضی 5 و 5 و 7 و 8 و 9 و 10 و 10 و 10 و 12 و 13 و 14 و 14 و 14 و 15 و 15 و 17 و 18 و 19 و 20 و 20 مشخص می کنیم هر داده چند تکرار دارد.

داده ی 5 دو تکرار دارد. داده 10 سه تکرار دارد. داده 14 سه تکرار دارد. داده 15 دو تکرار دارد و داده 20 دو تکرار دارد. و بقیه داده ها یک تکرار دارند. می بینیم که داده 10 و 14 که هر کدام سه تکرار دارند بیشترین فراوانی را دارند بنابراین می توان گفت این داده ها دو مد دارند که برابر با 10 و 14 است.

کدام معیار مرکزی را انتخاب کنیم؟

در تفسیر و تحلیل مسائل آماری در نظر گرفتن تنها یک شاخص گرایش به مرکز کافی نیست می بایست هر سه معیار میانگین، میانه و مد محاسبه شود و براساس هدف مورد بررسی، معیار مناسب انتخاب و از آن برای انجام تفسیر، قضاوت و پییش بینی مورد استفاده قرار گیرد.

به طور کلی برای برنامه ریزی و تصمیم گیری میانگین بهتر از میانه است.

مشاهده ای که تفاوت بسیار زیادی با سایر مشاهدات مجموعه داده ها داشته باشد را داده دور افتاده می گویند، داده دور افتاده میانگین داده ها را تحت تاثیر قرار داده در حالی که تاثیری بر میانه و مد داده ها ندارد.

بنابراین اگر داده ی دور افتاده داشتیم نباید میانگین را بعنوان شاخص مرکزی در نظر بگیریم. بلکه باید از میانه استفاده کنیم.

اگر همه ی داده ها در عددی ضرب یا با عددی جمع شوند شاخص مرکزی چه تغییری می کند؟

به طور کلی اگر میانگین داده های $x_{1},x_{2},…,x_{n}$ برابر $\overline{x}$ باشد و مد این داده ها برابر $M$ باشد و میانه داده ها برابر $Q2$ باشد آنگاه میانگین، مد و میانه داده های $ax_{1}+b, ax_{2}+b , … , ax_{n}+b$ به ترتیب برابر $a\overline{x}+b$ و $aM+b$ و $aQ2+b$ هستند.

نکته کاربردی: اگر مقدار داده ها بزرگ باشد و محاسبات سخت باشد می توان مقدار عددی مشخص را از همه داده ها کم کرد و برای داده های جدید میانگین را بدست آورد و بعد آن مقداری که از همه ی داده ها کم کردیم را دوباره به مقدار میانگین بدست آمده اضافه می کنیم تا میانگین داده های اصلی بدست آید.

جمع بندی

در این مقاله به آموزش شاخص های مرکزی یعنی میانگین مد چارک اول چراک دوم یا میانه و چارک سوم پرداختیم. اگر علاقمند به یادگیری اصطلاحات درباره داده های آماری، جدول فراوانی و نمودارهای آماری و شاخص های پراکندگی دارید به هر کدام از این مقالات مراجعه کنید لطفا ما را از نظرات خود در مورد مقاله شاخص های مرکزی بهره مند کنید.

هر آنچه که باید درباره ی شاخص های مرکزی میانگین میانه چارک ها و مد بدانید

شاخص مرکزی میانگین چیست و چگونه بدست می آید؟

اگر داده ها دسته بندی شده بودند چطور میانگین داده ها را بدست آوریم؟ (میانگین موزون)

شاخص مرکزی میانه چگونه بدست می آید؟

چارک ها چگونه بدست می آیند؟ چارک اول، چارک دوم، چارک سوم

مد چه نوع شاخص مرکزی ای می باشد؟

کدام معیار مرکزی را انتخاب کنیم؟

اگر همه ی داده ها در عددی ضرب یا با عددی جمع شوند شاخص مرکزی چه تغییری می کند؟

دیدگاهتان را بنویسید لغو پاسخ

آخرین مطالب وبلاگ

دنباله های عددی

تابع خطی و معادله خط

تابع و دامنه و برد آن

تعیین علامت

عبارت و معادله گویا

معادله درجه دوم

معادله

عبارت جبری

قدرمطلق

دوره ها

دسترسی سریع

دسترسی سریع

مقالات مادر