جامع ترین دایره المعارف از اصطلاحات داده های آماری
در این مقاله به آموزش اصطلاحات آماری می پردازیم و هرآنچه که باید از انواع کمیت روشهای نمونه گیری و گردآوری داده ها باید بدانید را در این مقاله می بینید. جامعه، نمونه، پارامتر، آماره و داده را تعریف می کنیم. انواع روش های نمونه گیری و انواع کمیت ها را بیان می کنیم. روش های گرد آوری داده ها را توضیح می دهیم و معایب و مزایای هر کدام را بیان می کنیم. اگر علاقمند به دانستن جزئیات این تعاریف هستید، این آموزش کامل ترین و آسان ترین آموزش موجود است.
بخش اول: تعریف اصطلاحات آماری
برای اینکه در مورد علم آمار مطالعه کنیم باید تعریف چند اصطلاح را بدانیم. در ادامه به تعریف برخی از اصطلاحات آماری می پردازیم. برای اینکه هر کدام را بهتر متوجه شوید هر کدام از اصطلاحات را در مثال فرضی بیان می کنیم.
مثال: می خواهیم بدانیم میانگین قد دانش آموزان پایه یازدهم کل کشور چند سانتی متر است.
داده: داده ها واقعیت هایی درباره یک چیزند که در محاسبه، استنباط، یا برنامه ریزی و پیش بینی به کار می روند. در این مثال به قد هر کدام از این بچه ها که در اختیار ما قرار می گیرد داده می گویند.
واحد آماری : واحد آماری به هر یک از افراد یا چیزهایی می گویند که داده های مربوط به آنها در یک بررسی آماری گردآوری می شود. در این مثال به هر کدام از این بچه ها واحد آماری می گویند.
جامعه آماری : مجموعه ی کل واحدهای آماری را جامعه آماری می نامند. در این مثال به همه ی دانش آموزان پایه یازدهم کل کشور، جامعه آماری می گویند.
نمونه: هر زیرمجموعه از جامعه آماری را که با روش مشخصی انتخاب شده باشد، یک نمونه می نامند. در این مثال به همه دانش آموزان پایه ی یازدهم مدارس نمونه دولتی کشور نمونه می گویند.
نمونه تصادفی: نمونه ای را که در آن، همه ی اعضای جامعه، شانس انتخاب یکسان در نمونه را داشته باشند نمونه تصادفی می نامند. در این مثال به همه دانش آموزان پایه یازدهم مدارس انتخاب شده در کشور، به این صورت که از هر شهر یک مدرسه دلخواه را انتخاب کنیم، نمونه تصادفی می گویند.
پارامتر جامعه: یک مشخصه عددی است که توصیف کننده جنبه ای خاص از جامعه است و در صورتی که داده های کل جامعه در اختیار باشند قابل محاسبه است. پارامتر مقداری ثابت است و این مقدار مجهول است و آمارگیری از کل جامعه همیشه امکان پذیر نیست به همین دلیل از آماره ها برای تخمین پارامترها استفاده می کنند. در این مثال به میانگین قد همه ی دانش آموزان پایه یازدهم کل کشور پارامتر جامعه می گویند.
آماره نمونه: مشخصه ای عددی که توصیف کننده ی جنبه ای خاص از نمونه است و از داده های نمونه بدست می آید. در این مثال به میانگین قد دانش آموزان پایه یازدهم در نمونه (همه مدارس نمونه دولتی یا نمونه تصادفی)، آماره نمونه می گویند.
متغیر: هر ویژگی از اشیا یا اشخاص، که در اعضای جامعه یکسان نیست و معمولا از یک عضو به عضو دیگر تغییر می کند را متغیر می گویند و عددی که به آن ویژگی یک عضو نسبت داده می شود را مقدار متغیر، یا مشاهده می گویند. در این مثال قد دانش آموزان پایه یازدهم متغیر است.
انواع متغیر
متغیرها از نظر نوع متغیر به دو دسته کیفی و کمی تقسیم می شوند.
متغیر کمی : متغیری است که مقادیر عددی می گیرد و برای آن عملیات ریاضی از قبیل جمع تفریق و معدل گیری قابل انجام است. متغیر های کمی از نظر مقیاس اندازه گیری به دو دسته فاصله ای و نسبتی تقسیم می شوند.
متغیر کیفی: متغیری است که صرفا برای دسته بندی افراد یا اشیا در گروه ها به کار می رود و لزوما مقدار عددی نمی گیرد. متغیر های کیفی از نظر مقیاس اندازه گیری به دو دسته اسمی و ترتیبی تقسیم می شوند.
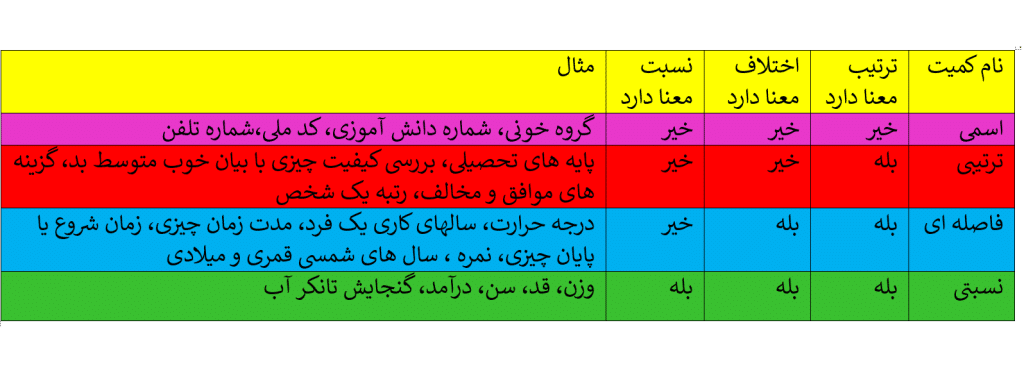
داده ها را به دو گروه کمی و کیفی تقسیم کردیم. می توان متغیرهای داده ها را در چهار مقیاس اندازه گیری دسته بندی کرد. اندازه گیری در تعریف به معنی ایجاد تفکیک بین افراد یا اشیا است. بسته به دقتی که این اندازه گیری صورت می گیرد آن را به چهار مقیاس اسمی، ترتیبی، فاصله ای و نسبتی تقسیم می کنیم. هدف از شناسایی این مقیاس ها تعیین نوع محاسبه ی مناسب برای داده ها است نظیر ترتیب، محاسبه ی اختلاف و نسبت گرفتن.
کمیت اسمی: این مقیاس برای متغیرهایی است که شامل نام ها برچسبها و گروه ها می شود. هیچ معیاری که با آن بتوان داده ها را از کوچک به بزرگ مرتب کرد وجود ندارد.
کمیت ترتیبی: این مقیاس با استفاده از الفاظ، ضمن ایجاد تفکیک بین افراد یا اشیا، ارجحیت قائل می شود. مقیاس ترتیبی برای متغیرهایی است که قابل مرتب کردن هستند و در عین حال محاسبه اختلاف بین مقادیر داده ها یا امکان پذیر نیست یا بی معناست. مثل رتبه کنکور، سطح تحصیلات (کارشناسی ارشد دکترا)
کمیت فاصله ای: این مقیاس به دلیل استفاده از لوازم یا قواعد دقیق اندازه گیری ویژگی افراد یا اشیا به دقت اندازه گیری می شود. به بیان دیگر مقیاس فاصله ای برای داده هایی است که قابل مرتب کردن هستند و همچنین اختلاف بین مقادیر داده ها بامعناست. در این مقیاس صفر قراردادی است. ضرب در این مقیاس بی معنا است.
کمیت نسبتی: این مقیاس برای داده هایی است که قابل مرتب کردن هستند و اختلاف بین مقادیر داده ها و نسبت مقادیر داده ها نیز بامعنا است. در این مقیاس صفر به معنای نبود ویژگی در فرد یا شی است. اندازه گیری هایی با واحد کیلوگرم، متر یک نوع کمیت نسبتی هستند.
برای اینکه تشخیص دهیم در یک کمیت، اختلاف معنا دار هست یا نه باید ببینیم نسبت اختلاف دو مقدار از متغیر به واحد آن متغیر ربط دارد یا نه. مثلا درجه حرارت واحد سانتی گراد و فارنهایت دارد اگر چهار مقدار را از درجه حرارت یک مکان داشته باشیم چه این مقادیر برحسب سانتی گراد باشند چه فارنهایت می بینیم که نسبت
بدون توجه به واحد اندازه گیری مقدار یکسانی است.
برای اینکه تشخیص دهیم که نسبت معنا دارد یا نه کافی است امتحان کنید. مثلا اینکه سن یک نفر دو برابر دیگری باشد معنا دارد اما اینکه بگوییم که ساعت 10 دوبرابر ساعت 5 است معنا ندارد. یا مثلا درجه حرارت یک شهر 20 درجه و شهر دیگر 10 درجه است اینکه این دو دما را با هم جمع کنیم معنا ندارد. اما اینکه وزن یک کیسه میوه 5 کیلو و وزن کیسه دیگر از این میوه 8 کیلو است مجموع وزن این دو کیسه 13 کیلو است معنا دارد.
توجه: اگر فقط یک متغیر از داده ها اندازه گیری شده باشد به جای ذکر مقیاس متغیر از واژه مقیاس داده ها استفاده می کنند. یعنی مثلا اگر برای یک نمونه هم قد و هم جنسیت را بخواهیم بدانیم “قد” یک متغیر و “جنسیت ” یک متغیر دیگر است. اما اگر فقط قد یک نمونه را بخواهیم در این صورت به جای اینکه بگوییم “متغیر قد” می گوییم “داده ی قد”.
داده ها در واقع اطلاعات مربوط به موضوع هستند و متغیر ویژگی مورد بررسی داده ها می باشد. مثلا افرادی که کوه دنا را طی می کنند، آدم ها، داده ها هستند و وزن و قد افراد و زمان طی شده به قله متغیر می باشند.
نمونه گیری و انواع آن
نمونه گیری : نمونه گیری ، فرآیند انتخاب نمونه ای از یک جامعه ، به منظور تعمیم اطلاعات آن به جامعه است.
نمونه گیری تصادفی ساده : نمونه گیری تصادفی ساده نوعی روش نمونه گیری که در آن همه ی واحدهای آمارای برای انتخاب شدن در نمونه احتمال یکسان دارند.
مزیت نمونه گیری ساده : همه ی داده ها برای انتخاب شدن در نمونه احتمال یکسان دارند.
محدودیت نمونه گیری ساده : دسترسی به همه ی داده ها دشوار و هزینه بر است.
انجام نمونه گیری تصادفی ساده درعمل با دشواری هایی همراه است. اگر اندازه جامعه بزرگ باشد، یعنی تعداد واحدهای آماری زیاد باشند، دسترسی به فهرستی از اعضای جامعه و دسترسی به اعضای انتخابی، دشوار و ممکن است هزینه بر باشد.
نمونه گیری خوشه ای : نمونه گیری خوشه ای نمونه گیری که در آن ، واحدهای نمونه گیری اولیه در جامعه ، گروه ها یا خوشه ها باشند. سپس همه ی واحدهای آماری خوشه های انتخاب شده را به عنوان نمونه در نظر می گیرند.
در خوشه ها هر چه ویژگی ها متفاوت باشند بهتر است.
نمونه گیری خوشه ای سریع تر و مقرون به صرفه تر است.
نمونه گیری طبقه ای : نمونه گیری طبقه ای روش نمونه گیری که در آن با طبقه بندی جامعه به زیر جامعه های مجزا یک نمونه تصادفی ساده از هر طبقه انتخاب می شود.
در طبقات هر چه ویژگی ها همگن باشد بهتر است
نمونه گیری سامان مند یا سیستماتیک : نوعی نمونه گیری طبقه ای است که در آن اندازه طبقات با هم برابر است فقط از طبقه اول، واحد آماری به تصادف انتخاب می شود و با همان رویه از طبقات دیگر، این کار انجام می گیرد.
نمونه گیری احتمالی : نمونه گیری ای است که همه ی واحدهای آماری احتمالی معلوم برای انتخاب در نمونه داشته باشد و از روشی تصادفی برای انتخاب واحدهای نمونه استفاده شود.
توجه: اگر یک روش نمونه گیری از نمونه گیری ایده آل فاصله بگیرد و به سمتی خاص انحراف پیدا کند می گویند آن روش نمونه گیری اریب است. لذا آمارشناسان تلاش می کنند تا با شناسایی منابع تولید اریبی، نمونه گیری ها را تا جایی که می توانند نااریب کنند.
بخش دوم: آمارگیری
حالا مثلا همه ی این ها یعنی جامعه، نمونه، پارامتر و آماره را می دانیم. حالا چطور باید این داده ها را جمع آوری کنیم و پارامتر یا آماره مربوط به آن را محاسبه کنیم. در ادامه چندین اصطلاح در مورد آمارگیری را تعریف می کنیم. تا در بخش سوم نحوه جمع آوری داده ها را آموزش ببینیم.
آمار: به مطالعه نحوه گردآوری سازمان دهی تحلیل و تفسیر داده ها برای استخراج اطلاعات و تصمیم گیری آمار گفته می شود.
اگر در آمار در جایی به یک نتیجه شسته رفته برخوردید، خیلی احتیاط کنید. بدست آوردن یک استنباط درست از داده ها تنها چیزی نیست که شما در یک بررسی آماری خواهان آن هستید خواسته ی دیگر ما برنامه ریزی و تصمیم گیری است.
گاهی هیچ آمار درست یا غلطی وجود ندارد، و همه چیز به این بستگی دارد که شما چرا می خواهید از آنها استفاده کنید.
آمار توصیفی: طبقه بندی خلاصه کردن توصیف و تفسیر اطلاعات جمع آوری شده و برقراری ارتباط از طریق آنها را آمار توصیفی می نامند.
آمار استنباطی : با استفاده از اطلاعات جمع آوری شده از نمونه کوچکی از آزمودنی ها، ویژگی های جامعه ای را که نمونه از آن انتخاب شده است برآورد یا استنباط کنند را آمار استنباطی می گویند. در واقع از جامعه نمونه انتخاب می کنیم بعد محاسبات آماره را انجام می دهیم بعد با جای گذاری اعداد نمونه برآورد پارامتر را انجام می دهیم.
برآورد نقطه ای : برآورد نقطه ای پارامتر جامعه برابر است با مقدار عددی حاصل از جای گذاری اعداد نمونه تصادفی در آماره نظیر آن پارامتر . به بیان دیگر مقدار عددی آماره را برآورد یا برآورد نقطه ای می نامند.
آمارگیری: گردآوری داده ها به یکی از روش های ممکن ( این روش ها در بخش سوم بحث می شوند)
آمارگیر: کسی که آمارگیری را انجام می دهد.
بخش سوم: روش های گردآوری داده ها
الان که می دانیم پارامتر آماره و متعیر و داده هر کدام چه هستند، مسئله مهم این است که چطور داده ها را گردآوری کنیم که بتوانیم پارامتر یا آماره مربوط به متغیر را بدست آوریم.در واقع چهار روش برای گردآوری داده ها وجود دارد: مشاهده – مصاحبه – پرسش نامه – دادگان ها. در ادامه به تعریف هر کدام از آنها می پردازیم.
مشاهده : گردآوری داده ها بدون نیاز به فرد پاسخگو، مانند شمارش تعداد وسایل نقلیه عبوری از یک تقاطع در هر ساعت یا اندازه گیری وزن محصولات یک باغ میوه.
پرسش نامه : مجموعه سوالات از پیش تعیین شده که توسط تعدادی پاسخگو تکمیل می شود. این روش مرسوم ترین ابزار گرفتن اطلاعات از مردم است.
مصاحبه : معمولا بین دو نفر صورت می گیرد یکی مصاحبه گر ( آمارگیر) و دیگری مصاحبه شونده یا پاسخگو است. این روش بیشتر زمانی استفاده می شود که آمارگیر از همه ی پاسخ های ممکن اطلاع کافی ندارد. و مصاحبه از صاحب نظران راه حل مناسبی برای گردآوری داده ها است.
دادگان : شامل مجموعه ای از اطلاعات ذخیره شده است در بسیاری از موارد داده ها را می توان از اطلاعاتی که قبلا ذخیره شده است بدست آورد.
همه ی این روش ها محدودیت هایی دارند در زیر محدودیت هر کدام از آنها را می خوانیم:
محدودیت مشاهده : اگر به دقت زیادی نیاز باشد این روش مناسب نیست
محدودیت پرسش نامه : اگر تعداد واحدهای نمونه زیاد باشد این روش زمان بر است.
محدودیت دادگان ها : همیشه اطلاعات ثبتی در اختیار نیست.
مشاهده یا نقطۀ داده ای در آمار: منظور از مشاهده یا نقطۀ داده ای در آمار، مجموعه ای است شامل یک یا چند مقدار اندازه گیری شده برای یک عضو جامعه آماری (واحد آماری).
مثلا اگر واحدهای آماری، دانش آموزان کلاس باشند و سن و قد و وزن و گروه خونی آنان متغیرها باشند. مقادیر این متغیرها برای هر کدام از دانش آموزان، یک “مشاهده” است.
نکته مهم: نتایج آماری باید توسط فردی که نه تنها روش ها بلکه موضوع مورد بحث را کامل درک کرده باشد تفسیر شود.
جمع بندی
در این مقاله به آموزش اصطلاحات آماری پرداختیم دانستن این اطلاعات بعنوان پیش نیاز برای آموختن شاخص های مرکزی و شاخص های پراکندگی و جدول فراوانی و نمودارهای آماری ضروری می باشد. اگر علاقمند به یادگیری هر کدام از این مباحث هستید لطفا به مقاله مربوطه مراجعه کنید. لطفا نظرات خود را در مورد مقاله اصطلاحات درباره داده های آماری در قسمت کامنت ها بیان کنید.