همه چیز درباره توابع مثلثاتی (تناوب، سینوس ، کسینوس و تانژانت)
توابع مثلثاتی شامل سینوس، کسینوس و تانژانت مانند سایر توابع دارای دامنه و برد هستند و می توان آنها را رسم کرد و از شکل هر تابع اطلاعاتی بدست آورد. در این مقاله به آموزش هر سه نوع از توابع مثلثاتی می پردازیم. به متناوب بودن این توابع اشاره می کنیم و دوره تناوب هر کدام را بیان می کنیم. همچنین به بیان توابع مثلثاتی در حالت کلی می پردازیم. اگر علاقمند به یادگیری توابع مثلثاتی هستید هرگز این مقاله را از دست ندهید. برای اینکه این مقاله برای شما مفید واقع شود حتما اول به مقالات تعریف نسبت های مثلثاتی و روابط مثلثاتی مراجعه کنید و به مطالعه آنها بپردازید.
تناوب چیست؟ به چه تابعی توابع متناوب می گویند؟
تناوب به معنای تکرار یک تابع در بازه های مختلف است. تابعی که در بازه های مختلف تکرار شود تابع متناوب نام دارد. به طور کلی تابع متناوب را به صورت زیر تعریف می کنیم:
تعریف: تابع را متناوب می نامیم هرگاه یک عدد حقیقی مثبت مانند
موجود باشد به طوری که برای هر
داشته باشیم
کوچک ترین عد مثبت با این خاصیت را دوره تناوب
می نامیم.
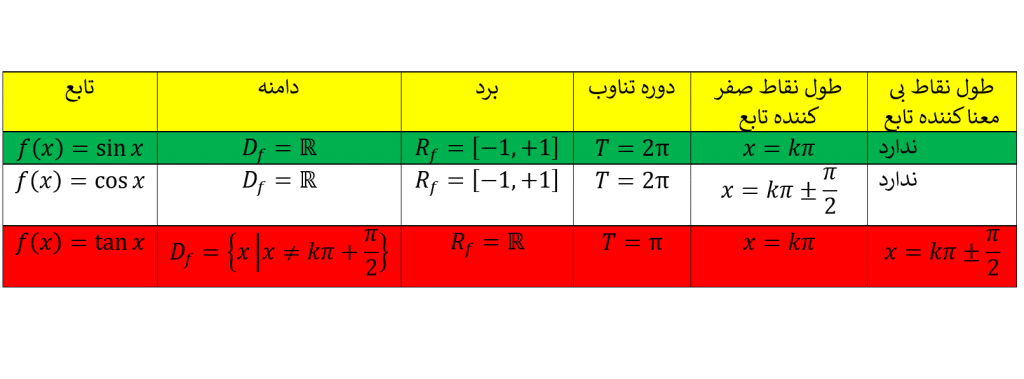
نکته: توابع مثلثاتی توابعی متناوب هستند.
تابع سینوسی چه شکل ، دامنه و بردی دارد؟
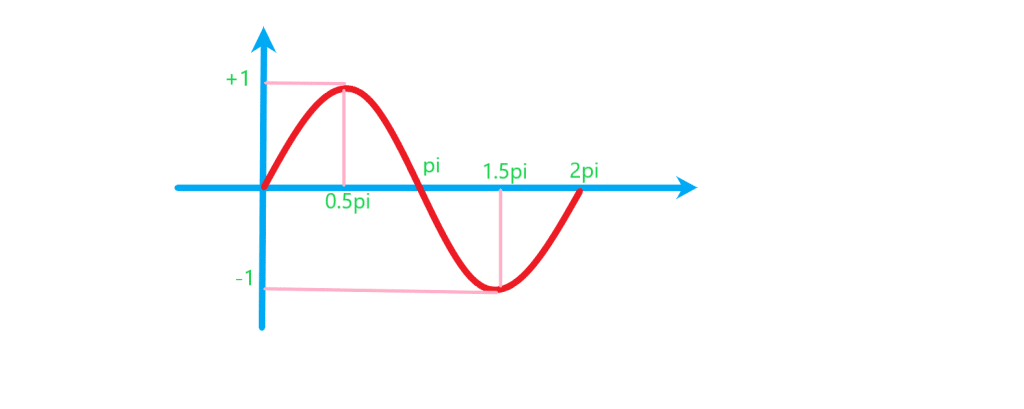
تابع سینوسی یک تابع با ضابطه ی یا
است. شکل این تابع به صورت زیر است.
همانطور که از شکل تابع پیداست مقدار تابع بین و
است یعنی
. پس برد تابع را می توان به صورت
همچنین می بینیم به جای هر مقداری از اعداد حقیقی را می توان قرار داد. پس دامنه این تابع همه ی اعداد حقیقی است.
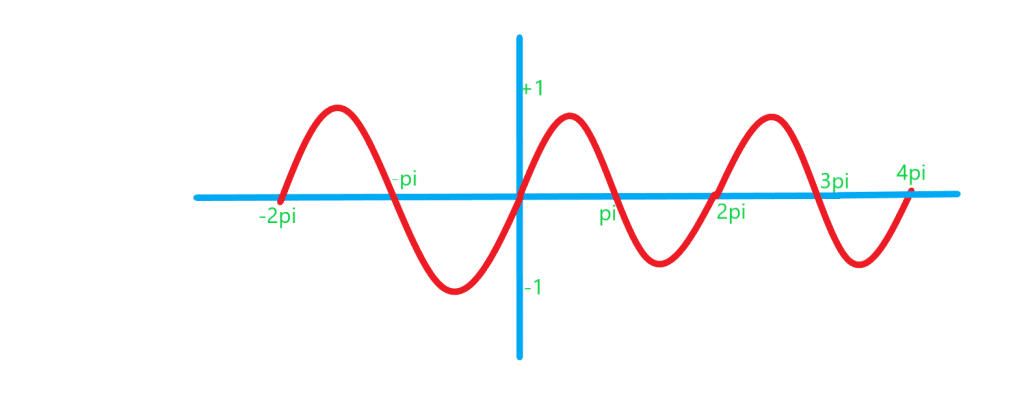
در شکل بالا می بینیم که این تابع در بازه های تکرار می شود. بنابراین می توان گفت دوره تناوب این تابع برابر
است می نویسیم:
تابع در نقاط
که
محور
ها را قطع می کند و مقدار صفر دارد.
شکل تابع سینوس در یک تناوب به صورت زیر است:
تابع کسینوسی چه شکل ، دامنه و بردی دارد؟
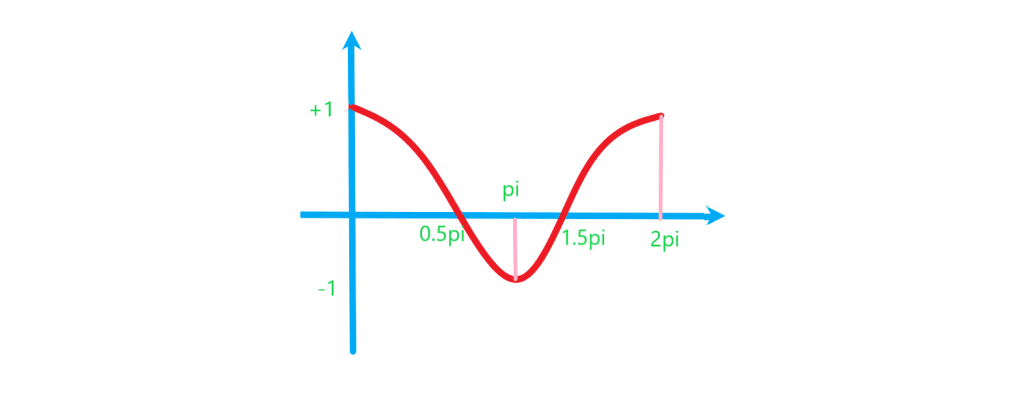
تابع کسینوسی یک تابع با ضابطه ی یا
است. شکل این تابع به صورت زیر است:
همانطور که از شکل تابع پیداست مقدار تابع بین و
است یعنی
. پس برد تابع را می توان به صورت
همچنین می بینیم به جای هر مقداری از اعداد حقیقی را می توان قرار داد. پس دامنه این تابع همه ی اعداد حقیقی است.
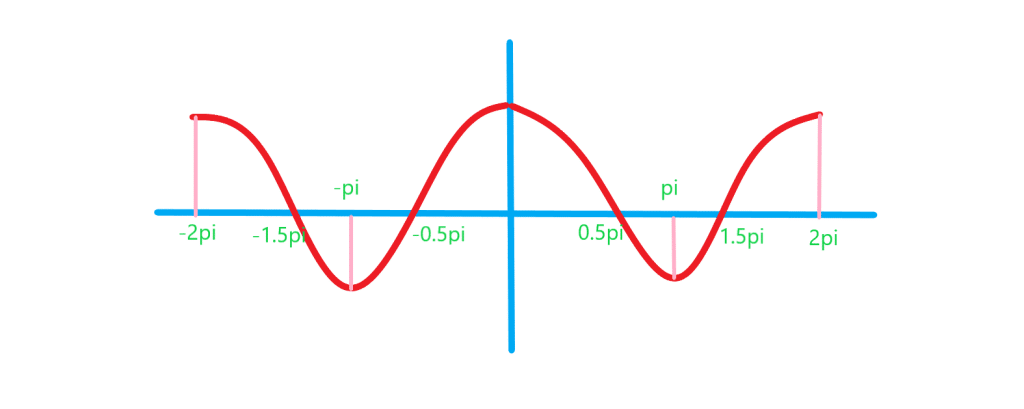
در شکل بالا می بینیم که این تابع در بازه های تکرار می شود. بنابراین می توان گفت دوره تناوب این تابع برابر
است می نویسیم:
تابع در نقاط
که
محور
ها را قطع می کند و مقدار صفر دارد.
شکل تابع کسینوسی در یک دوره تناوب به صورت زیر است:
در حالت کلی چطور یک تابع مثلثاتی را رسم کنیم؟
تابع های و
را توابع مثلثاتی گویند. گاهی به نمودار تابع
موج سینوسی و به نمودار تابع
موج کسینوسی نیز می گویند.
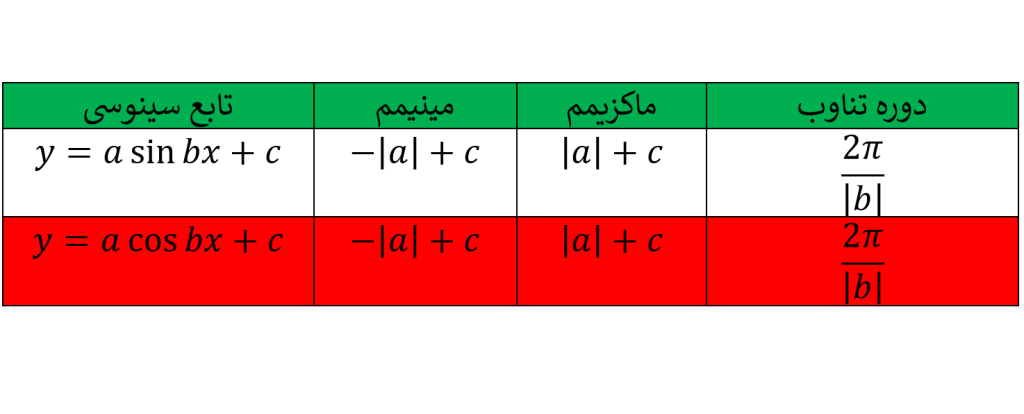
در حالت کلی توابع مثلثاتی را می توان به صورت و
نوشت. اگر تابعی با این ظاهر با ضرایب اعداد حقیقی
و
دارای مقدار ماکزیمم
و مقدار مینیمم
و دوره تناوب
است.
بنابراین با داشتن ضابطه تابعی به صورت فوق می توان مقادیر ماکزیمم و مینیمم و دوره تناوب تابع را به دست آورد و برعکس با داشتن مقادیر ماکزیمم، مینیمم و دوره تناوب یک تابع مثلثاتی، می توان ضابطه تابع مورد نظر را به دست آورد.
مثال: ماکزیمم، مینیمم و دوره تناوب توابع زیر را بدست آورید.
حالا باید طبق فرمول هایی که در بالاتر گفته شد مقادیر ماکزیمم، مینیمم و دوره تناوب را بدست آوریم:
با توجه به معادلات کلی و
می توان توابع مثلثاتی را رسم کرد به این صورت که با توجه به مقدار ماکزیمم و مینیمم می توانیم مقادیر ماکزیمم و مینیمم
را بدست می آوریم. بعد یک دوره از تابع را رسم می کنیم بعد با توجه به دوره تناوبِ تابع، آن شکل را تکرار می کنیم.
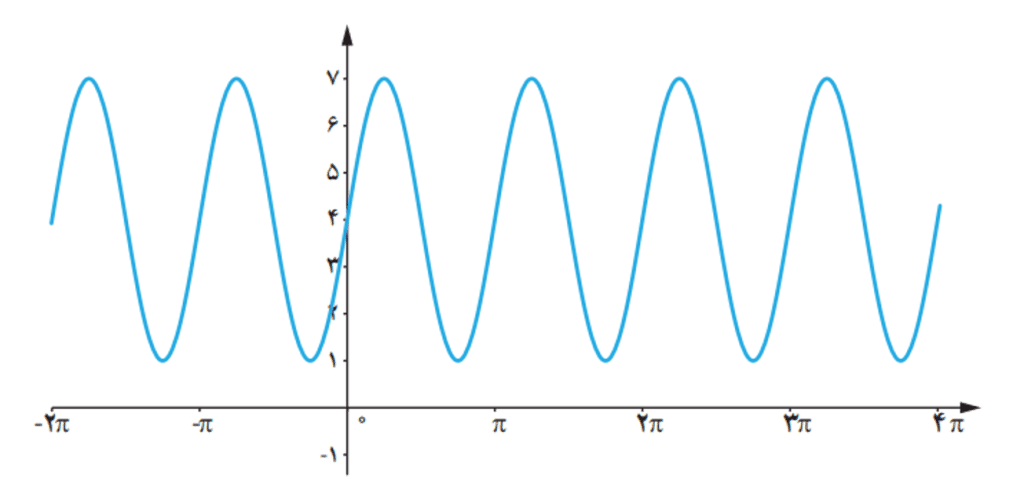
مثال: توابع و
را رسم کنید.
جواب: برای رسم تابع ابتدا تابع را در یک دوره تناوب رسم می کنیم. یعنی در گام اول دوره تناوب تابع را پیدا می کنیم
پس باید تابع را در بازه
تا
رسم کنیم. در گام دوم چون تابع سینوسی است از شکل تابع سینوس در یک دوره از تناوب که در بالاتر در بخش تابع سینوسی نشان داده شده است استفاده می کنیم یعنی تابع سینوس را رسم می کنیم. در گام سوم با توجه به مقادیر ماکزیمم و مینیمم و میانگین این دو یعنی
، سه مقدار اصلی
را بدست می آوریم . حالا سه مقدار اصلی تابع سینوسی که بدست آمد از طرفی می دانیم اول و آخر مقدار دامنه در یک بازه از دوره تناوب به صورت
و
است با داشتن این اعداد و شکل تابع سینوس در یک دوره تناوب می توانیم تابع را رسم کنیم و در گام آخر شکل بدست آمده را مرتب تکرار می کنیم تا نشان دهیم تابع متناوب است.
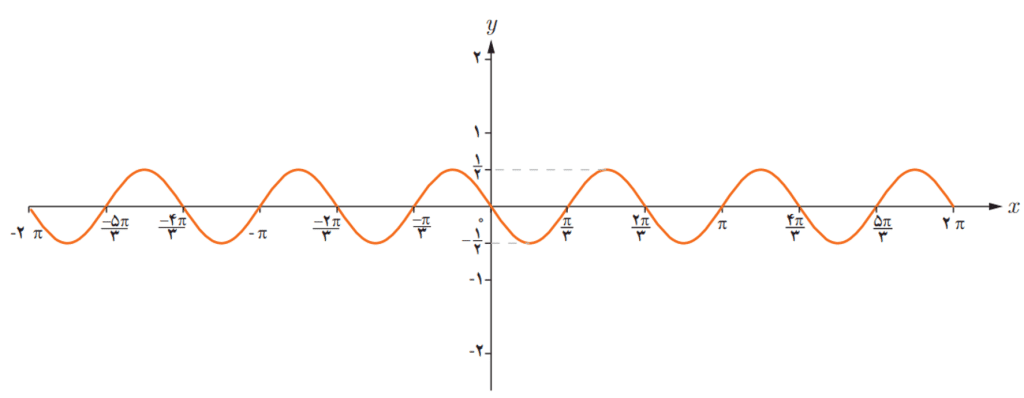
برای رسم تابع ابتدا تابع را در یک دوره تناوب رسم می کنیم. یعنی در گام اول دوره تناوب تابع را پیدا می کنیم
پس باید تابع را در بازه
تا
رسم کنیم. در گام دوم چون تابع کسینوسی است از شکل تابع کسینوس در یک دوره از تناوب که در بالاتر در بخش تابع کسینوسی نشان داده شده است استفاده می کنیم یعنی تابع کسینوس را رسم می کنیم. در گام سوم با توجه به مقادیر ماکزیمم و مینیمم و میانگین این دو، سه مقدار اصلی را بدست می آوریم که برابرند با
. حالا سه مقدار اصلی تابع کسینوسی که بدست آمد از طرفی می دانیم اول و آخر مقدار دامنه در یک بازه از دوره تناوب به صورت
و
است با داشتن این اعداد و شکل تابع کسینوس در یک دوره تناوب می توانیم تابع را رسم کنیم و در گام آخر شکل بدست آمده را مرتب تکرار می کنیم تا نشان دهیم تابع متناوب است.
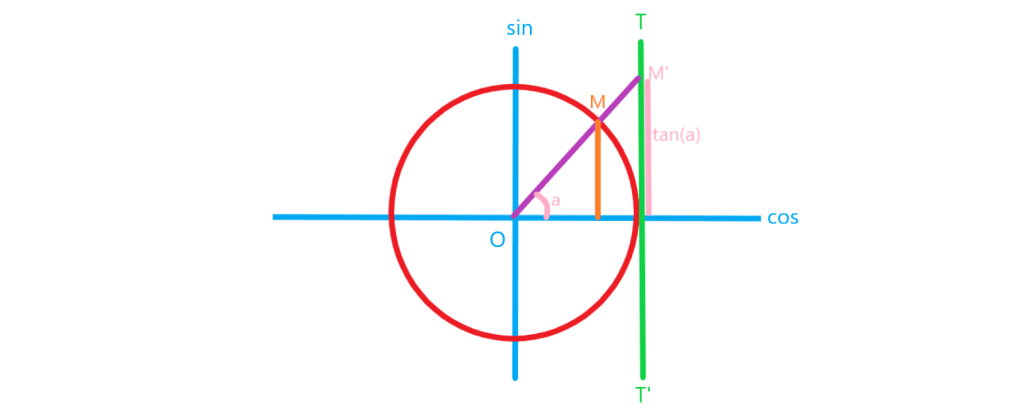
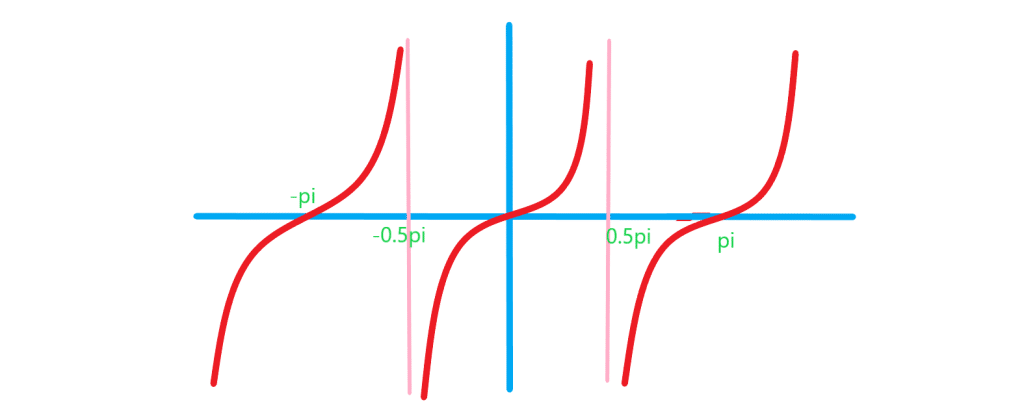
تابع تانژانت تعریف تابع ، شکل تابع و دامنه و برد آن
به ازای هر زاویه دلخواه در دایره مثلثاتی (به جز
)، عددی حقیقی به عنوان
داریم و تابعی با ضابطه
مشخص می کند دامنه این تابع به صورت زیر بدست می آید:
و برد آن مجموعه اعداد حقیقی است. تابع متناوب است و دوره تناوب آن
است:
مقدار تانژانت زاویه با توجه به دایره مثلثاتی زیر بدست می آید:
همه ی نکات مربوط به توابع مثلثاتی را می توانید در جدول های زیر مشاهده کنید:
جمع بندی
در این مقاله به آموزش توابع مثلثاتی پرداختیم. سینوس، کسینوس و تانژانت توابع مثلثاتی هستند که در این مقاله هر کدام از آنها را بررسی کردیم دامنه و برد و دوره تناوب هر کدام را بیان کردیم. به آموزش رسم هر کدام از این توابع پرداختیم. اگر علاقمند به آموختن چیزهای بیشتری درباره مثلثات هستید لطفا به مقالات تعریف نسبت های مثلثاتی، روابط بین نسبت های مثلثاتی و معادلات مثلثاتی مراجعه کنید. لطفا ما را از نظرات خود در مورد مقاله توابع مثلثاتی بیان کنید.


2 پاسخ
چقدر خوب رسم نمودار سینوس کسینوس رو توضیح دادید فهمیدم بالاخره 😍😍🤩🤩
خوشحالم برات مفید بوده عزیزم