یک آموزش کامل درباره نسبت های مثلثاتی سینوس، کسینوس، تانژانت و دایره مثلثاتی

مثلثات به بررسی روابط بین زوایا و اضلاع یک مثلث می پردازد و یکی از اهداف این علم، اندازه گیری فاصله ها به صورت غیر مستقیم است. در این مقاله به آموزش تعریف نسبت های مثلثاتی، بدست آوردن نسبت های مثلثاتی برخی زوایا، تبدیل واحدهای اندازه گیری زاویه یعنی رادیان و درجه به یکدیگر پرداختیم. همچنین دایره مثلثاتی و نواحی آن را معرفی کردیم. اگر علاقمند به یادگیری در مورد روابط بین نسبت های مثلثاتی، معادله مثلثاتی و نمودار و توابع مثلثاتی هستید لطفا به مقالات مربوطه مراجعه کنید. اما اگر به پیش نیازی برای خواندن این مقالات نیاز دارید و علاقمند هستید تا مثلثات را از ریشه و پایه یاد بگیرید این مقاله را از دست ندهید.

نسبت های مثلثاتی در یک مثلث قائم الزاویه

مثلثات به بررسی روابط بین زوایا و اضلاع یک مثلث می پردازد و یکی از اهداف این علم، اندازه گیری فاصله ها به صورت غیر مستقیم است.

در مثلث قائم الزاویه $ABC$ نسبت های زیر تعریف می شوند:

$\sin {A}=\frac{BC}{AC}$

$\cos {A}=\frac{AB}{AC}$

$\tan {A}=\frac{BC}{AB}$

$\cot {A}=\frac{AB}{BC}$

در نتیجه می توان گفت

$\tan{A}=\frac{\sin{A}}{\cos{A}}\,\,\,,\,\,\,\cot{A}=\frac{\cos{A}}{\sin{A}}$

در یک مثلث قائم الزاویه، نسبت های سینوس، کسینوس، تانژانت و کتانژانت را نسبت های مثلثاتی می نامیم.

نکته: طبق قضیه فیثاغورس داریم:

$AB^{2}+BC^{2}=AC^{2}$

$\rightarrow \,\,\, \frac{AB^{2}}{AC^{2}}+\frac{BC^{2}}{AC^{2}}=\frac{AC^{2}}{AC^{2}}$

$\rightarrow \sin^{2}{A}+\cos^{2}{A}=1$

چطور اندازه ی نسبت های مثلثاتی یک زاویه را بدست آوریم؟

با کمک مربع می توان نسبت های مثلثاتی زاویه 45 درجه را می توان بدست آورد. با کمک مثلث متساوی الاضلاع می توان نسبت های مثلثاتی زاویه 30 و 60 درجه را بدست آورد.

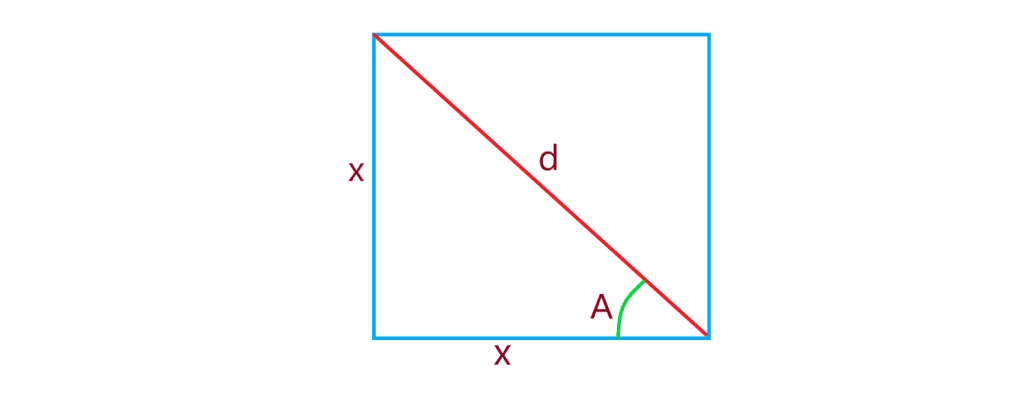
مثلا برای بدست آوردن نسبت های مثلثاتی 45 درجه ابتدا یک مربع رسم می کنیم سپس یکی از قطر های این مربع را رسم می کنیم بعد رابطه ی فیثاغورس را برای مثلث قائم الزاویه ی ایجاد شده می نویسیم داریم:

$x^{2}+x^{2}=d^{2}\,\,\,\rightarrow \,\,\, 2x^{2}=d^{2}\,\,\,\rightarrow \,\,\,d=\sqrt{2}x$

$\sin{A}=\frac{x}{d}=\frac{x}{\sqrt{2}x}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$

$\cos{A}=\frac{x}{d}=\frac{x}{\sqrt{2}x}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$

$\tan{A}=\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}}=1$

$\cot{A}=\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}}=1$

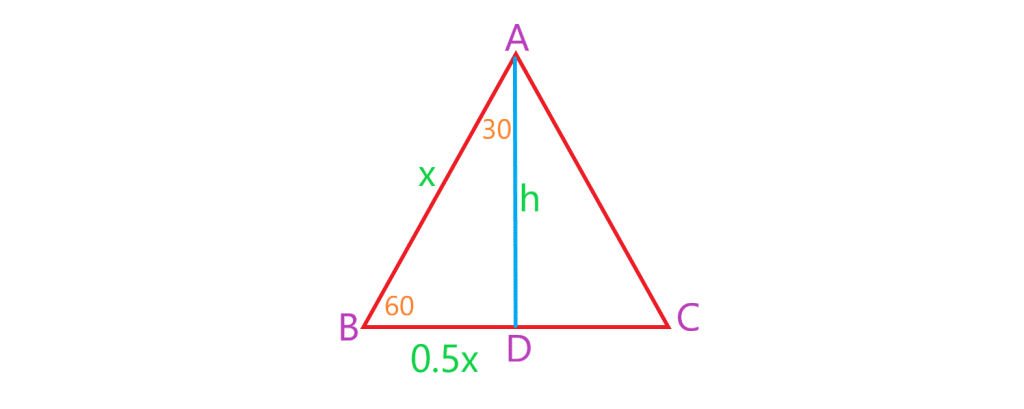
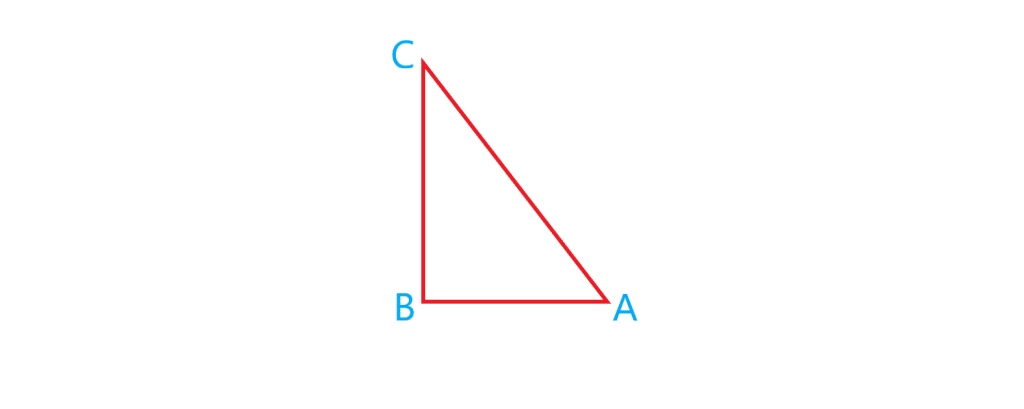
برای بدست آوردن نسبت های مثلثاتی 60 و 30 درجه یک مثلث متساوی الاضلاع رسم می کنیم می دانیم در مثلث متساوی الاضلاع همه ی زاویه ها برابر 60 درجه هستند. همچنین ارتفاع همان نیمساز و همان میانه است پس اگر اندازه یک ضلع $x$ باشد اندازه $BD$ برابر است با $\frac{x}{d}$ حالا با توجه به اینکه $ABD$ یک مثلث قائم الزاویه است ما می توانیم روابط مثلثاتی را برای این مثلث بنویسیم. داریم:

ابتدا رابطه ی فیثاغورس را برای مثلث قائم الزاویه $ABD$ می نویسیم:

$h^{2}+(\frac{x}{2})^{2}=x^{2}\,\,\,\rightarrow \,\,\, h^{2}=x^{2}-(\frac{x}{2})^{2}$

$\rightarrow \,\,\, h^{2}=(1-\frac{1}{4})x^{2}=\frac{3}{4}x^{2}\rightarrow h=\frac{\sqrt{3}}{2}x$

سپس نسبت های مثلثاتی برای زاویه 60 درجه را می نویسیم:

$\sin{60}=\frac{h}{x}=\frac{\frac{\sqrt{3}}{2}x}{x}= \frac{\sqrt{3}}{2}$

$\cos{60}=\frac{\frac{x}{2}}{x}=\frac{1}{2}$

$\tan{60}=\frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}= \sqrt{3}$

$\cot{60}=\frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}}= \frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$

در آخر نسبت های مثلثاتی زاویه 30 درجه هم بدست می آید:

$\sin{30}=\frac{\frac{x}{2}}{x}=\frac{1}{2}$

$\cos{30}=\frac{h}{x}=\frac{\frac{\sqrt{3}}{2}x}{x}= \frac{\sqrt{3}}{2}$

$\tan{30}=\frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}}= \frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$

$\cot{30}=\frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}= \sqrt{3}$

می بینیم با استفاده از تعریف نسبت های مثلثاتی و با کمک اشکال هندسی مربع و مثلث می توانیم نسبت های مثلثاتی زاویه 30 و 45 و 60 درجه بدست آوریم.

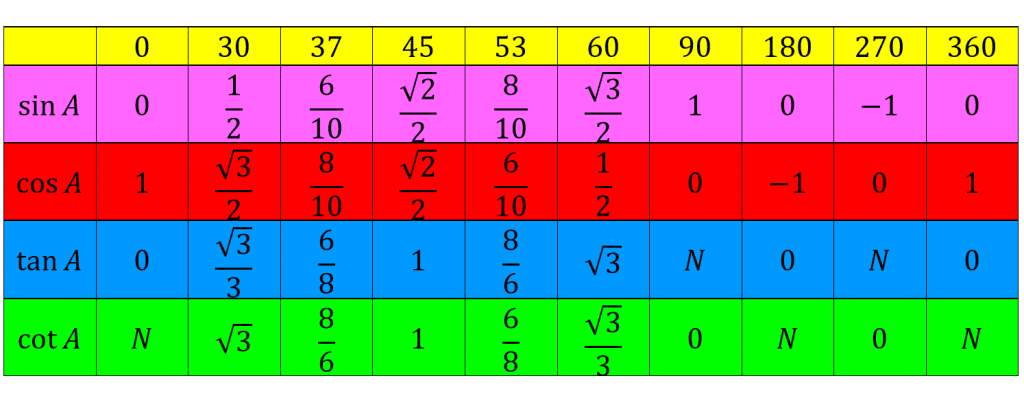
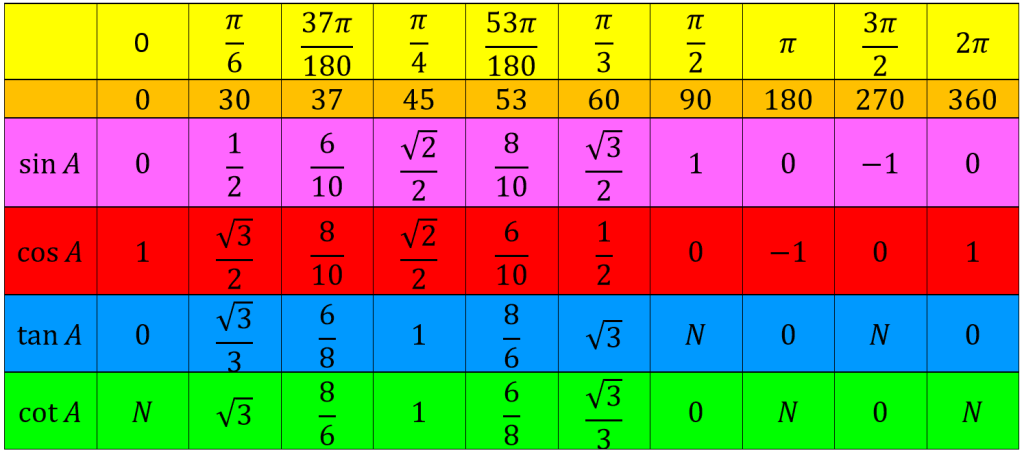
برای برخی از زوایا نسبت های مثلثاتی محاسبه شده اند که به طور نمونه برخی از آنها را در بالاتر محاسبه کردیم. در جدول زیر می توانید نسبت های مثلثاتی آنها را ببینید:

توچه: $N$ در این جدول به معنای بی معنا یا نامعلوم می باشد.

رادیان یکی از واحدهای اندازه گیری زاویه

یک رادیان در هر دایره دلخواه اندازه زاویه ای مرکزی است که طول کمان رو به رو به آن برابر طول شعاع دایره است معمولا از نماد $rad$ برای نمایش اندازه یک زاویه بر حسب رادیان استفاده می شود.

نکته : همواره بین اندازه یک زاویه مانند $\theta$ برحسب رادیان و طول کمان $l$ روبرو به این زاویه در یک دایره به شعاع $r$ رابطه زیر برقرار است: $l=r\theta$ . در این رابطه $l$ و $r$ هم واحدند.

نکته : اگر $D$ اندازه زاویه ای بر حسب درجه و $R$ اندازه آن بر حسب رادیان باشد آنگاه:

$\frac{D}{180}=\frac{R}{\pi}$

مثال: اگر اندازه زاویه هایی برابر با 30 و 50 و80 و 200 درجه باشند. اندازه هر کدام از این زوایا برحسب رادیان چقدر است؟

جواب: برای اینکه بتوانیم این سوال را حل کنیم از فرمول $\frac{D}{180}=\frac{R}{\pi}$ برای هر کدام از این زوایا استفاده می کنیم.

$\frac{30}{180}=\frac{R}{\pi}\,\,\,\,\rightarrow \,\,\,R=\frac{30\pi}{180}=\frac{\pi}{6}$

$\frac{50}{180}=\frac{R}{\pi}\,\,\,\,\rightarrow \,\,\,R=\frac{50\pi}{180}=\frac{5\pi}{18}$

$\frac{80}{180}=\frac{R}{\pi}\,\,\,\,\rightarrow \,\,\,R=\frac{80\pi}{180}=\frac{4\pi}{9}$

$\frac{200}{180}=\frac{R}{\pi}\,\,\,\,\rightarrow \,\,\,R=\frac{200\pi}{180}=\frac{10\pi}{9}$

بنابراین جدول زوایا را می توان به صورت زیر بازنویسی کرد:

توجه: $N$ در این جدول به معنای بی معنا یا نامعلوم می باشد.

دایره مثلثاتی چه ویژگی هایی دارد؟

اگر محیط دایره ای را به 360 کمان مساوی تقسیم کنیم، اندازه زاویه مرکزی روبه روی هر کدام از این کمان ها 1 درجه است. اندازه هر کمان با زاویه مرکزی روبه روی آن کمان بر حسب درجه برابر است.

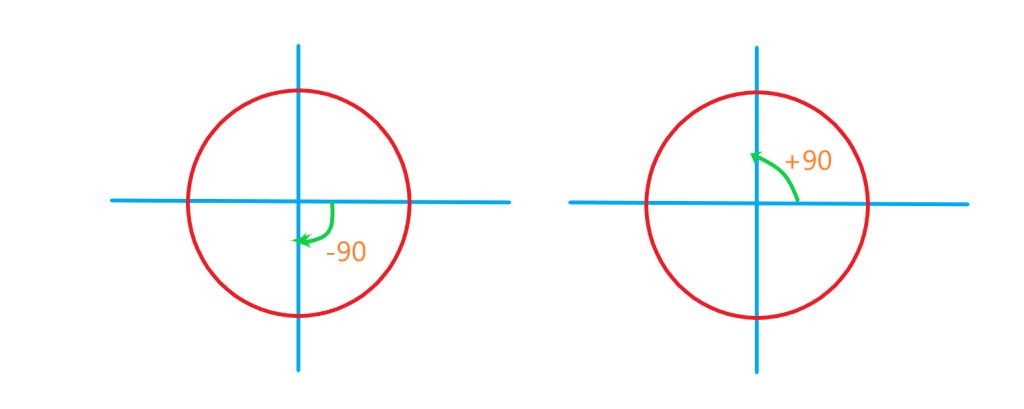
دایره مثلثاتی دایره ای است به شعاع واحد که جهت مثبت آن برخلاف گردش عقربه های ساعت است. به این جهت، جهت مثلثاتی می گوییم. معمولا مرکز این دایره مبدا مختصات است.

چطور نسبت های مثلثاتی را با کمک دایره مثلثاتی بدست آوریم؟

فرض کنید نقطه ای دلخواه مانند $P(x,y)$ نقطه ای دلخواه روی دایره مثلثاتی زیر باشد و $\theta$ زاویه ای است که نیم خط $\overrightarrow{OP}$ با محور $\overrightarrow{Ox}$ می سازد. از نقطه $P$ خطی بر محور $\overrightarrow{Ox}$ عمود می کنیم و محل برخورد را $Q$ می نامیم. با کمک مثلث $OPQ$ نسبت های مثلثاتی زاویه $\theta$ به صورت زیر بدست می آید:

$\sin{\theta}=\frac{PQ}{OP}\,\,\,,\,\,\,\cos{\theta}=\frac{OQ}{OP}$

$\tan{\theta}=\frac{PQ}{OQ}\,\,\,,\,\,\,\cot{\theta}=\frac{OQ}{PQ}$

از آنجا که شعاع دایره برابر یک است پس $OP=1$ بنابراین می توان گفت

$\cos{\theta}=OQ\,\,\,\,,\,\,\,\,\sin{\theta}=PQ$

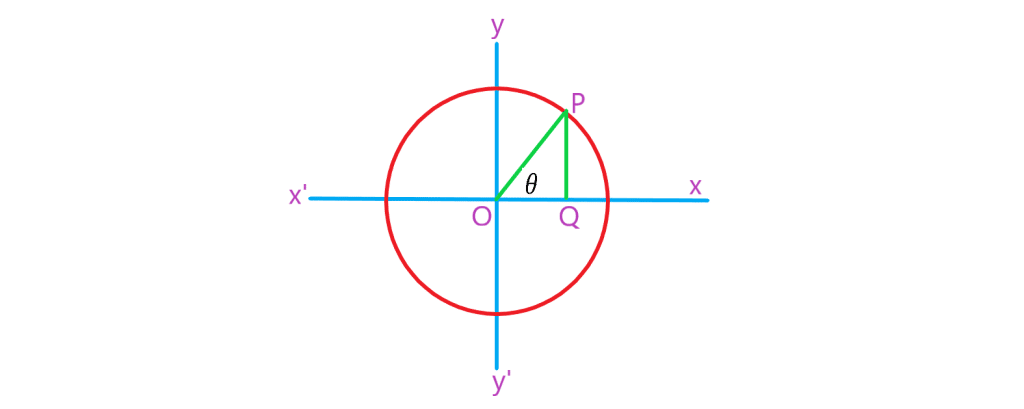
در این دایره محور $x^{'}ox$ یا محور مختصات $x$ ها را محور کسینوس ها و محور $y^{'}oy$ یا محور $y$ ها را محور سینوس ها می نامیم. بنابراین اگر نقطه دلخواه $P(x,y)$ را روی این دایره در نظر بگیریم می توان گفت:

$y=\sin{\theta}\,\,\,\,,\,\,\,\,x=\cos{\theta}$

نکته : اندازه سینوس و کسینوس هر زاویه دلخواه همواره کمتر از یک است. در واقع برای هر زاویه دلخواه $\alpha$ داریم:

$-1 \le \sin{\alpha} \le 1 \,\,\,\,\,,\,\,\,\,\, -1 \le \cos{\alpha} \le 1$

محورها دایره ی مثلثاتی را به چه ناحیه هایی تقسیم می کند؟

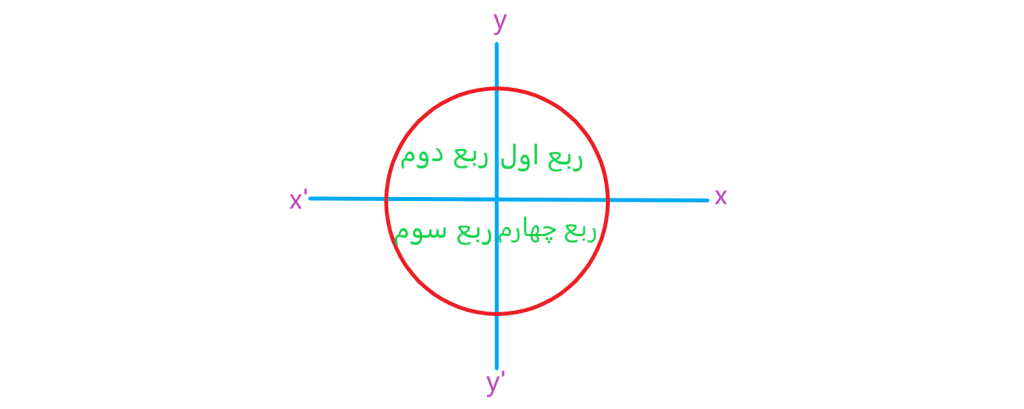
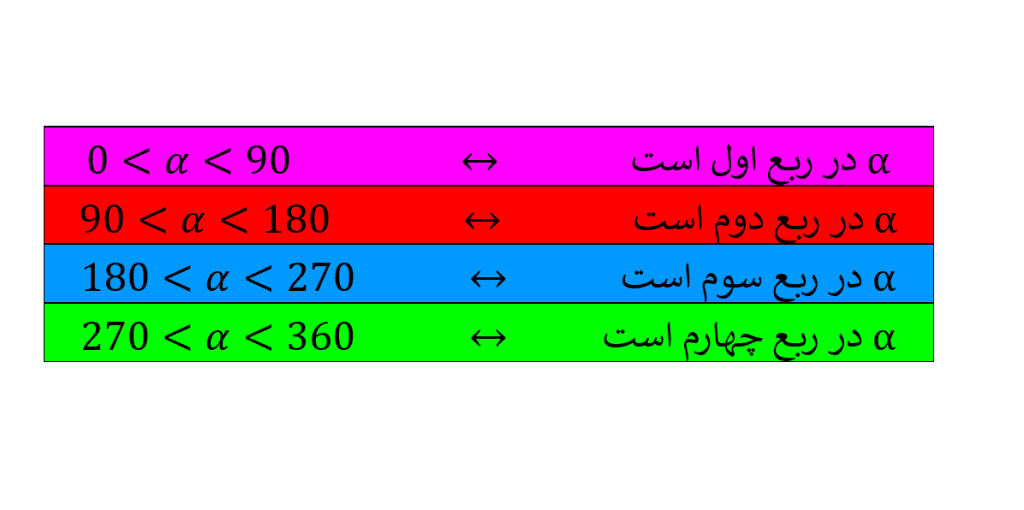
دو محور $x^{'}ox$ و محور $y^{'}oy$ صفحه را به چهار قسمت تقسیم می کنند. هر یک از این قسمت ها را یک ناحیه یا یک ربع مثلثاتی می نامیم. با توجه به جهت دایره مثلثاتی، ناحیه $xoy$ را ربع اول، ناحیه $x^{'}oy$ را ربع دوم، ناحیه $x^{'}oy^{'}$ را ربع سوم و ناحیه $xoy^{'}$ را ناحیه چهارم مثلثاتی می نامیم.

نکته: زاویه های 0 و 90 و 180 و 270 و 360 درجه زوایای مرزی هستند و آنها را در هیچ کدام از ناحیه های فوق در نظر نمی گیریم.

نکته: اگر یک زاویه دلخواه $\alpha$ در دایره مثلثاتی داشته باشیم با توجه به اینکه این زاویه در کدام بازه قرار می گیرد جایگاهش در دایره مشخص می شود. داریم:

در ربع اول سینوس و کسینوس و تانژانت و کتانژانت همگی مثبت هستند.

در ربع دوم سینوس مثبت است. اما کسینوس، تانژانت و کتانژانت منفی هستند.

در ربع سوم سینوس و کسینوس منفی هستند. اما تانژانت و کتانژانت منفی هستند.

در ربع چهارم کسینوس مثبت است. اما سینوس، تانژانت و کتانژانت منفی هستند.

مثال: اگر کتانژانت یک زاویه و سینوس همان زاویه هم علامت باشند آنگاه آن زاویه در کدام ناحیه مثلثاتی قرار دارد؟ با توجه به آنچه در جدول بالا می بینیم، در ناحیه اول سینوس و کتانژانت هر دو مثبت اند. در ناحیه چهارم هر دو منفی اند. پس زاویه مورد نظر یا در ناحیه اول قرار دارد یا در ناحیه چهارم.

جمع بندی

در این مقاله علوم پایه ی مثلثات تدریس شده است. بدست آوردن نسبت های مثلثاتی از طریق مثلث قائم الزاویه، نسبت های مثلثاتی برخی زوایای مهم و روش بدست آوردن آن ها، تبدیل رادیان و درجه به یکدیگر ، دایره مثلثاتی و محاسبه نسبت های مثلثاتی از طریق دایره مثلثاتی و بررسی ناحیه های مثلثاتی و علامت نسبت های مثلثاتی در هر ناحیه آموزش داده شده است. اگر علاقمند به سایر بخش های مثلثات هستید به مقاله روابط بین نسبت های مثلثاتی، معادلات مثلثاتی، نمودار و توابع مثلثاتی مراجعه کنید. لطفا ما را از نظرات خود در مورد مقاله تعریف نسبت های مثلثاتی در قسمت کامنت ها بهره مند کنید.

2 پاسخ

مهسا گفت:

آوریل 16, 2025 در 07:21

مرسیییی خیلی ممنون از مقاله جذاب تون
من جدول ها رو دانلود کردم و تو گوشی ام هست تا کم کم حفظ شون کنم
اینجوری تو مدرسه زودتر از همه سوال ها رو حل می کنم 🙈🙈🥰🥰

پاسخ
1. ریحانه حسینی گفت:
  
  آوریل 16, 2025 در 17:22
  
  خوشحالم برات مفید بوده عزیزم موفق باشی
  
  پاسخ

یک آموزش کامل درباره نسبت های مثلثاتی سینوس، کسینوس، تانژانت و دایره مثلثاتی

نسبت های مثلثاتی در یک مثلث قائم الزاویه

چطور اندازه ی نسبت های مثلثاتی یک زاویه را بدست آوریم؟

رادیان یکی از واحدهای اندازه گیری زاویه

دایره مثلثاتی چه ویژگی هایی دارد؟

چطور نسبت های مثلثاتی را با کمک دایره مثلثاتی بدست آوریم؟

محورها دایره ی مثلثاتی را به چه ناحیه هایی تقسیم می کند؟

2 پاسخ

دیدگاهتان را بنویسید لغو پاسخ

آخرین مطالب وبلاگ

دنباله های عددی

تابع خطی و معادله خط

تابع و دامنه و برد آن

تعیین علامت

عبارت و معادله گویا

معادله درجه دوم

معادله

عبارت جبری

قدرمطلق

دوره ها

دسترسی سریع

دسترسی سریع

مقالات مادر